基于交通网络图算法的驮背运输路径选择研究

安冬冬 , 王浩庆, 易洪波, 常 超

基于交通网络图算法的驮背运输路径选择研究

安冬冬1, 王浩庆2, 易洪波3, 常 超4

（1. 四川交通职业技术学院, 成都 611130；2. 四川交投实业有限公司, 成都 610023；3. 西南交通大学, 交通运输与物流学院, 成都 611756；4. 中国铁路太原局集团有限公司，侯马车务段, 山西 侯马 043000）

论文从驮背运输的政策背景和发展现状入手, 分析了现代运输行业的未来趋势, 即全球性与跨区域性的经济贸易活动越来越普及, 联运组织模式是大势所趋。论文采用交通网络图模拟运输节点与线路的连接形式, 将实际运行过程中的各项影响成本做了函数分析, 重点提出时间成本、费用成本和交通环境影响成本三个参数。在算法上, 论文将两种运输方式单独分开, 将模型中首末点和转运点的成本拟化成一条虚拟的线路, 形成符合传统最短路Floyd算法的网络图形, 并采用计算机编程求得最优方案的结果组合。

驮背运输; 路径选择; 交通网络图; Floyd算法

0 引 言

随着国家提出的一带一路、长江经济带等政策的推进，全球性与跨区域性的经济贸易活动越来越普及，货物种类与运输要求也更加多样化[1]。在传统运输模式中，物流企业或货运代理在选择运输方式时多考虑的是该种运输方式的优势是否符合自己的预期需求，缺乏综合运输形势的理念，时间与费用成本较为固定，几乎没有下降空间。近年来，交通运输部、国家发展改革委等部门出台了《关于开展多式联运示范工程的通知》、《推进物流大通道建设行动计划（2016—2020年）》等多个文件，均建议多种运输方式联合运输，将各自的运输优势在联运中发挥出来，结合中转站点，完成长距离大运量的货物运输，驮背运输则是加强专业化联运设备研发的重点项 目[2]。如何在实际联合运输中使差别化的运输方式充分发挥自身特点，如何选择合理的线路，在选定的节点中高效的转运，以满足现代物流市场中大运量、快速且经济的需求已成为目前交通运输业发展的重点方向。

1 驮背运输路径选择影响因素分析

驮背运输是多式联运中公铁联运模式的一种组织方式，由联运经营人在信息网络中转平台进行运输组织，运输过程中不会在中途转运点进行货物的拆分与拼装，仅做运输工具间简单的装卸中转工作。驮背运输的流程是汽车在联运中转点将自身集装箱挂车直接开上火车，通过铁路方式进行长距离运输后到达目的地再从火车上开下，直接运送到货主手中，是一种以公路甩挂运输模式为基础拓展的公铁联运作业形式[3]。

1.1 驮背运输过程影响因素

（1）公路运输

公路运输是运输方式中最基本的形式之一，在联运过程中一般负责短距离接驳与城市内道路运输，或在铁路线路绕行较大、首尾节点城市无铁路线路到达的情况下进行运输。公路路线一般在起讫点间有多种选择，由于受外部环境的不确定性影响较大，在线路选择时一般考虑以下几种因素的影响：

① 自然环境。道路运输受天气影响极大，如夏季与冬季时段，高温、大雾、大风、雨雪结冰等恶劣天气较多，货运车辆运输速度很慢，运输安全隐患也较多，也可能因为防晒、防雨、防潮、防冻等措施不够，导致货物本身受损。

② 道路环境。货物运输车辆一般体积较大，对道路线形、道路宽度、道路限高限重均有一定的要求，在线路选择时要重点考虑所选线路的道路环境。例如一些大件货物的车辆，若途经桥梁或下穿，最小通过高度则会受到桥梁宽度、最高承载等条件的限制[4]。

③ 交通环境。运输任务繁忙的时间段，公路道路常会遇到拥堵情况，特别是在经过城市道路路段。若遇到交通管制、早晚高峰期或一些道路限行政策等，均导致原本运输时间增长，影响后续阶段的转运及下一阶段的运输过程。

（2）铁路运输

对铁路运输而言，线路基础设施已确定，运载车辆只要满足运输相关要求即可，一般在申请时就已组织安排妥当。故路径的选择影响因素相较于公路运输而言较为简单，主要有以下几点：

① 自然环境。受自然灾害和季节天气的影响，铁路车辆行车安全性与速度都会降低，但相对于公路运输而言，影响概率与程度均不大。

② 线路环境。国家铁路线路为货物运输提供了货运专列铁路与客货共线铁路两类。在线路选择时，往往偏向于选择干扰较小、开行对数较少的客货共线铁路或货运专列铁路，但也需要综合考虑时间成本。此外，铁路线路也常穿过桥梁与隧道，同公路运输相同，也需要考虑货物的尺寸与重量[5]。

总的来说，驮背运输在运输过程中受各类影响因素较多，不能一味的以运输距离作为选择的唯一标准，应全面综合性考虑。

1.2 驮背中转过程影响因素

（1）转运组织方式

以货物由铁路运输转运至公路运输为例，转运组织方式一般为货物在车站货场承运，装车后向编组站集结，在技术站形成列车，行车至转运站点时，由各类专业技术以及与运能相匹配的机械设备对货物进行装卸搬运，再由汽车运输公司将货物装车，进行下一阶段的运输[6]。以货物集装箱由公路运输转运至铁路运输为例，采用驮背运输，该转运形式一般为货物由仓库货堆场以集装箱形式进行装车，行至转运站点时，牵引车将集装箱挂车直接开至铁路平板车上，停妥后甩下挂车离开，该集装箱挂车由铁路机车进行下一阶段的运输至前方转运点，再由另一辆牵引车提前准备等待，开上铁路平板车，挂上待运集装箱，继续下一阶段的运输。

（2）中转成本分析

① 中转时间成本

中转时间一般指装卸时间和滞留时间。中转时间成本指的是货物公铁两种运输方式转换所需要花费的总时间，也是货物运输车辆进入中转站点进行换装所停留的时间。由于运输时间与线路长度和运输速度直接相关，整个运输过程中时间不确定性的因素主要在中转环节，减少中转环节的时间浪费也是提高联运效率的关键[7]。

② 中转费用成本

中转费用成本主要包含装卸搬运费用和货物仓储费用等。驮背运输的货物体量较大，尤其对于大件货物，装卸搬运较复杂，在转运过程中对机械设备的牵引技术、操作空间和承重能力有着特殊的要求。

2 基于驮背运输模式的路径选择模型与求解

2.1 路径选择的成本构成

（1）时间成本（包括公路运输的交通影响 成本）

随着运输需求的多样化，货主对驮背运输模式的时效性需求增加，制定运输组织方式时，时间成本是运输路径选择考虑的重点。从驮背运输过程来看，总时间成本包括各阶段的运输时间（线段上的时间阻抗）与转运点的中转时间（节点上的时间阻抗）两个部分[8]。

此外，在计算公路运输时间成本时，需要考虑交通影响成本。由于驮背运输在公路运输阶段时都是由大型货运车辆承担运输，对自身车道前后车辆和相邻车道的车辆均有一定的影响。混合车道的车型不同，导致通行速度与单位时间交通量都很难达到道路设计通行能力，严重时会造成路段拥堵，直接影响运输过程中的时间成本，故驮背运输车辆在公路运输过程中对周围交通影响的成本不能忽视，需在路径选择中考虑。在计算公路运输时间成本时，设置交通影响系数，作为后续分析目标函数的路阻函数系数之一。公路运输方式的交通影响系数主要考虑大型车辆对公路通行能力的影响，故在计算时将该系数参照《道路通行能力》手册[9]中大型车辆的影响系数公式：

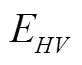
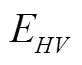
Tab.1 Conversion coefficient of vehicles in the road section

目标函数：

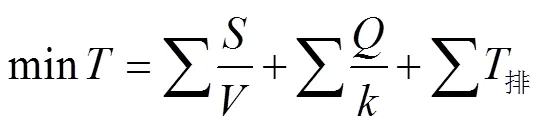
式中：

——运输距离，km；

——运行速度，km/h；

——货运量，t；

——单位时间转运能力，t/h；

（2）费用成本

费用成本是指在托运人选择驮背运输方式时所需要支付的金钱费用，涵盖运输费用和中转费用两个方面[10]。铁路运输方式费用成本主要以基本运价为主，另由杂费以及其他费用共同组成，基本运价包含发到基价和运行基价，其中发到基价为一次性支付的定值，运行基价为与运输距离相关的单位重量运价[11]。公路运输方式费用成本根据不同的运输形式计算方式有所不同，例如整车、零担、集装箱各自都有自己的收费模式。由于驮背运输货物的特征一般为大运量货物，为方便后续建模和求解，这里选择整车运输作为公路运输的代表，带入后文运输费用成本的计算。

中转费用成本一般由货物的换装量、换装设备和换装技术所决定[12]。在实际收费时，一般会直接根据货物的种类提供转运基价供运输企业选择。为简化模型，论文在计算中转费用时，直接用货物的运载量与单位中转价格的乘积带入模型。

2.2 基于交通网络图算法的路径选择模型

某生产企业有一批货物需要从生产地运往销售地（如图1所示），起终点城市仓库已确定，运输空间范围内有多条线路可以选择，采用驮背运输方式。在此情景下，论文建立基于交通网络图的驮背运输路径选择模型，主要解决的问题是在考虑整体时间成本、费用成本和交通影响的基础上，选择从货物起运地至到达地的最优运输方式和运输路径，使得时间成本（包括公路运输的交通影响成本）、费用成本在权重已定的情况下综合值最小。

图1 驮背运输路网示意图

根据以上条件，模型做出以下假设[13]：

（1）在交通网络图中，起终点间任意两个网络节点均双向联通，同种运输方式在两节点间往返两个方向的线路阻抗值相等。

（2）货物运量在起终点间无变化，货物在网络节点上最多发生一次运输形式的变换。

（3）任意两个相邻节点间均按照一定的速度匀速运输，且各条公路运输中驮背运输车辆对道路交通影响程度一致。

（4）同种运输形式在不同路段上运输速度无差别，单位运价固定。

（5）起讫两点的装货与卸货时间和费用按照转运点的单位成本的一半计入总成本。

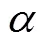
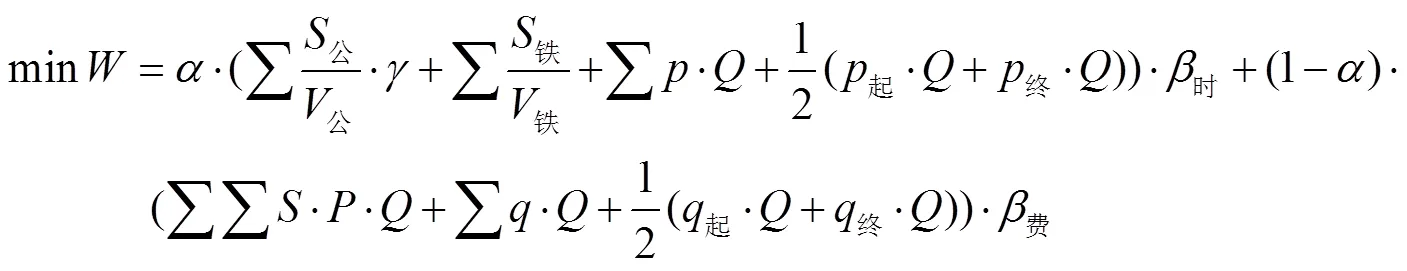
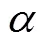
约束条件如下：

（1）两种运输方式承运能力的约束，货物作为整体形式存在，经过路径中某个路段时，货物的运量在道路及运载工具的能力承受范围之内。

（2）网络中各中转节点转运能力的约束，在绘制交通网络图时，已将转运能力不够的中间节点删去，一次驮背运输的货运量不能大于各中转节点转运能力。

（3）运输方式在各路段上的唯一性约束，任意两个相邻节点间仅能选择一种运输方式。

（4）在任意转运节点上运量的约束，联运货物总运量在运输过程中一直保持一致，进入和驶出中转节点时货物运量无变化。

2.3 模型求解

论文利用Floyd算法进行最短路求解，由于驮背运输的Floyd模型进行算法研究时与传统的图论算法有差异[14]。在进行算法设计的同时，需要解决以下几个问题：

（1）如图2所示，起终点均有两种运输方式可选，且起点和终点也需要进行货物的装和卸两个过程。为了便于表示，先将起终点转化为仓库点、公路运装点、铁路运装点三个节点。

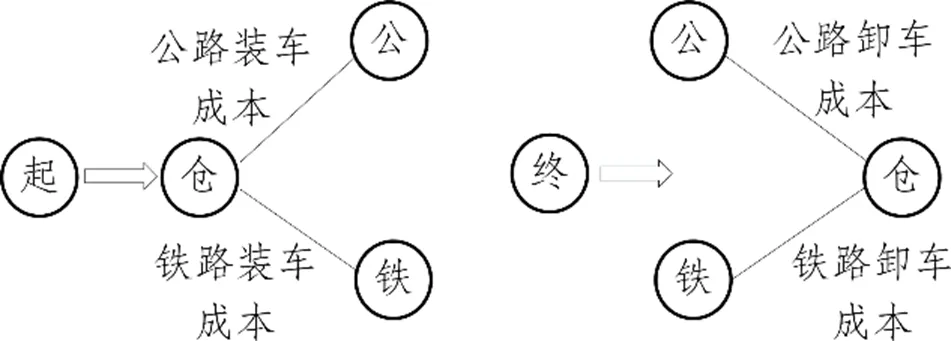
图2 驮背运输网络图点成本转化为线成本示意图 （起终点）

（2）传统的网络图在节点之间仅有一条线段代表阻抗。驮背运输路径选择问题中，任意相邻两点均可选择两种运输方式，在设计算法时，可将每个中转接点转化为两个点分别代表公路运输与铁路运输的固定节点，故在图3中每条线段在实际状况下由4条线段表达。

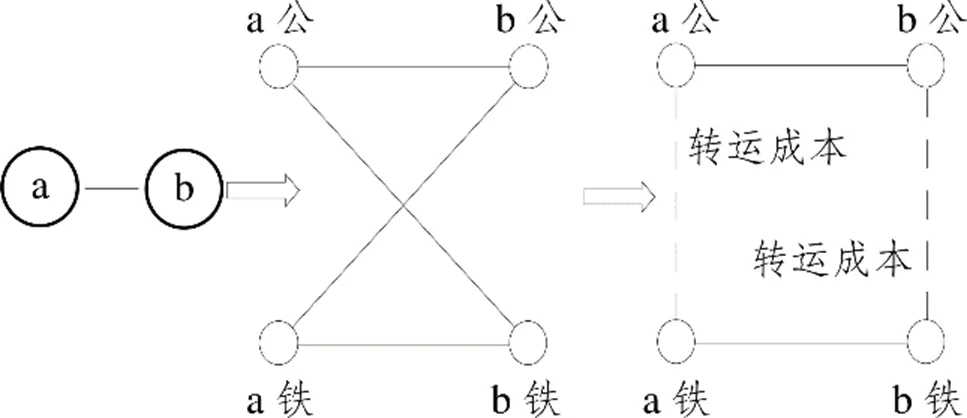
图3 驮背运输网络图点成本转化为线成本示意图 （内部节点）

（3）在传统最短路径算法中，节点处没有阻抗[15]，在选择时仅考虑边的阻抗值。驮背运输路径选择问题中，若选择某一转运点，则在该点上就包含了时间成本和费用成本。在设计算法时，需要将每个节点扩大为两个节点，并在其间用线段相连，代替表达运输方式的转运过程，其线段的阻抗值即为该点的转运成本，起终点同理。也就是说，若在某一点发生转运，就需要通过运输方式转换的这条虚拟的线段，若没有，则可以以该运输方式的固定节点进入下一步。

论文利用Java语言，对问题的算法进行描述。该算法以图4所示流程实现。

图4 驮背运输路径选择模型算法流程图

总的来说，整体算法中最核心的代码共5行，如下所示：

for（=1；<=；++）

for（=1；<=；++）

for（=1；<=；++）

if（dis[][]> dis [][] + dis [][]）

dis [][] = dis [][] + dis [][]；

3 算例分析

M市某生产企业生产一批货物，在行业市场上产品特点较为突出不可替代性较明显，现N市某企业订购一批该货物共600 t，时间敏感系数为0.55，该货物运输任务由某驮背运输企业承担。论文以M市为起点，N市为终点，沿途各大型城市为中转节点，绘制简化如图5所示交通网络图，各线段的运输方式均有铁路和公路两种。在该案例中，将网络中各线段与各节点作为研究对象，为驮背运输经营企业与货物托运人选择一条成本合理、运输高效的运输路径。

图5 案例网络图（单位：km）

在上图中，起终点用M点与N点表示，中途分别有A、B、C、D、E、F共6个转运节点，任两点间能够相互互通的路段共有11条。线段上数字左为公路运输距离，右为铁路运输距离。各点间线路长度、各转运节点的转运作业单位成本和速度单价见表2至表4。

初步计算得出算法初始线路阻抗矩阵表如表5所示。将该案例网络图按照上述算法设计的思路重新绘制，形成代入模型的基础网络图（图6所示），图中数字代表计算得出的线路阻抗值。

表2 案例网络图各线路长度表

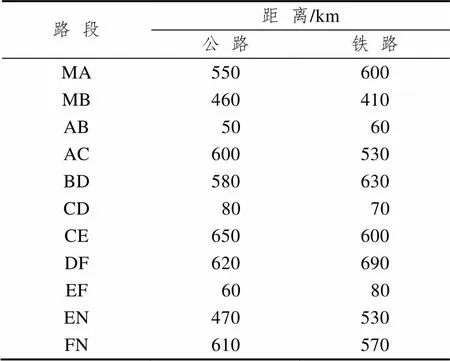
Tab.2 Length of each line in the network diagram of the case

表3 案例网络图各节点转运单位成本表

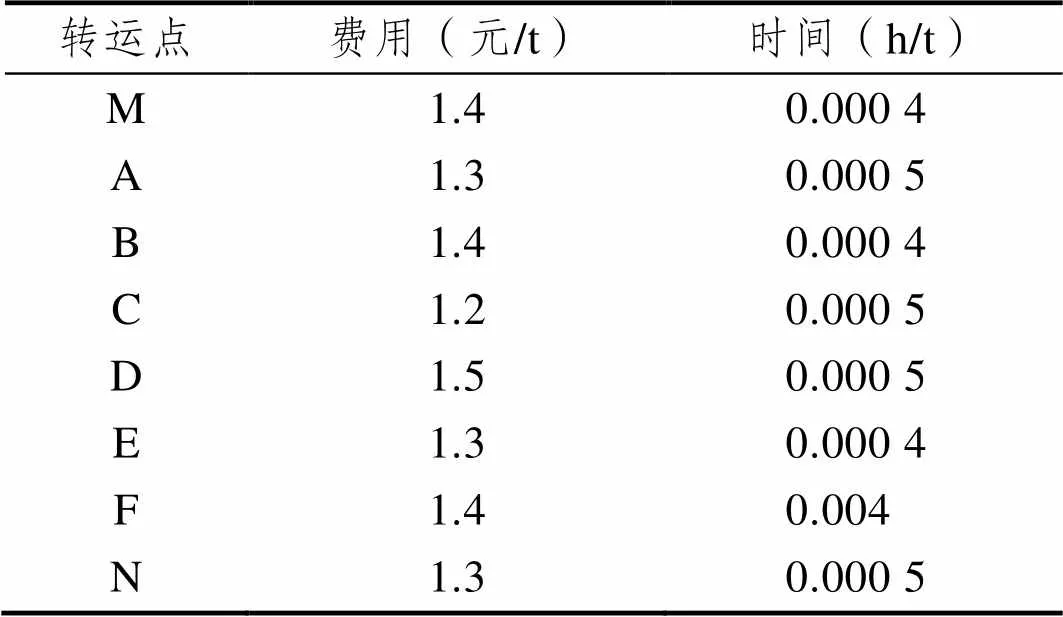
Tab.3 Network diagram of the case unit cost of each node transfer

表4 两种运输方式运输速度与运输单价表

Tab.4 Transportation speed and unit price of two modes of transportation

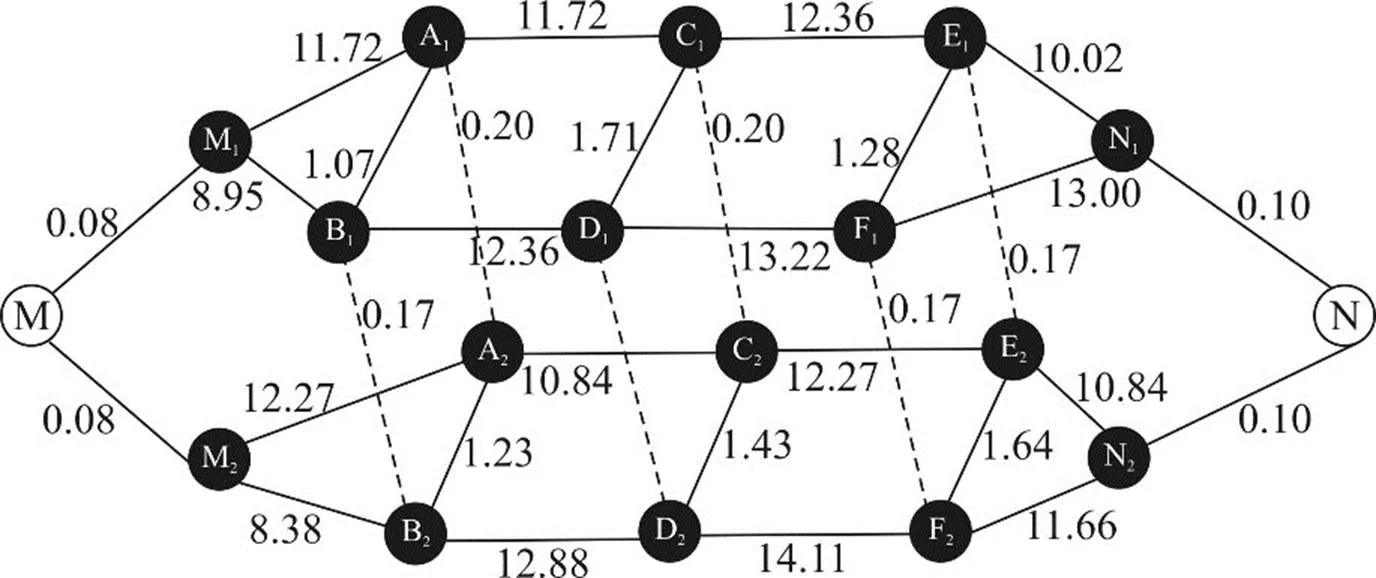
图6 案例网络模型计算图

表5 案例网络模型初始矩阵表

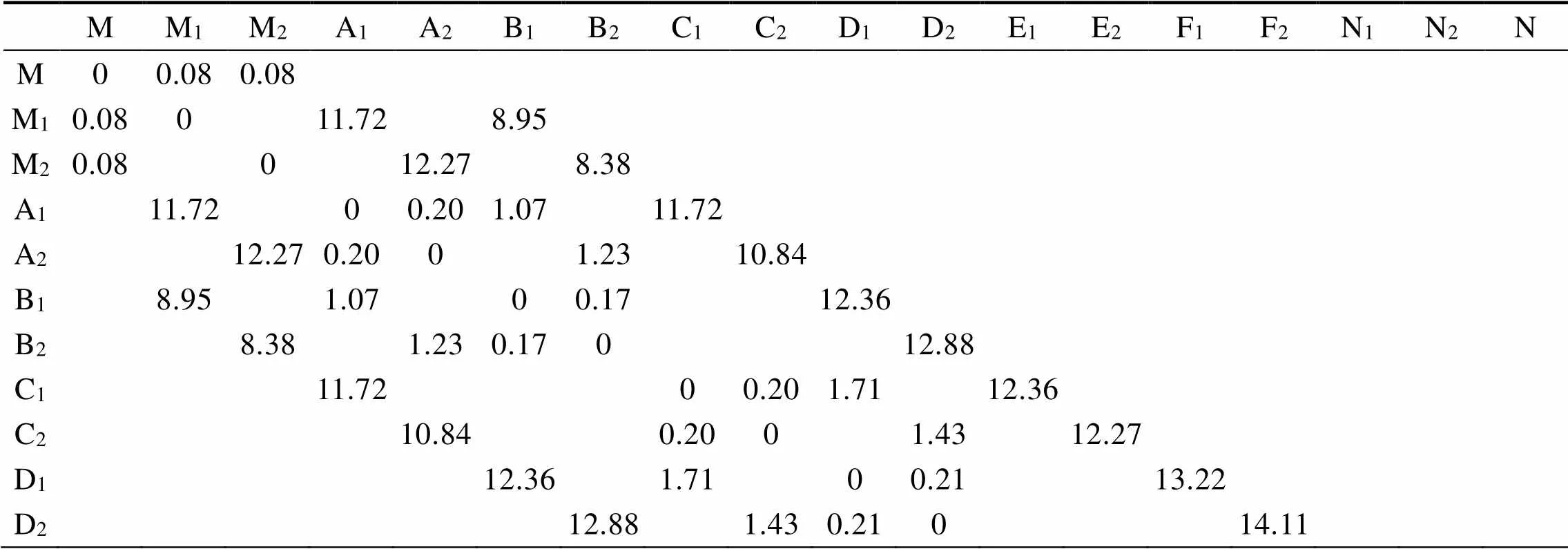
Tab.5 Initial matrix of the case network model

续表5

MM1M2A1A2B1B2C1C2D1D2E1E2F1F2N1N2N E1 12.36 00.171.28 10.02 E2 12.27 0.170 1.64 10.84 F1 13.22 1.28 00.1713.00 F2 14.11 1.640.170 11.66 N1 10.02 13.00 0 0.10 N2 10.84 11.66 00.10 N 0.100.100

将案例数据代入模型后的结果表明，在案例中货物托运人仅需要提供货物的运量600t与时间敏感系数值0.55，系统可以通过预先编辑好的路网，获得转换后的路网各段阻抗值。经过Floyd算法程序计算，得出最优路径方案结果为M→ B→A→C→E→N，从M→E为铁路运输并在E点进行运输方式转换，由铁路运输方式转换为公路运输方式，整个联运方案的时间成本为40.3 h，费用成本为464 490元。

4 结束语

在考虑货物托运人的时间敏感系数的基础上寻找最优路径方案（路线选择和运输方式组合），这与传统网络图最短路径单一目标值的问题解决方法并不一样。相同运输线路下运输转运点选择的不同会直接影响运输时间成本与费用成本，转运点固定的情况下运输线路不同也会有不同的方案结果。利用改进后的交通网络图Floyd算法，将转运成本转化到虚拟线路上，从而使整个运输过程成本计算更加清晰，为联运企业选择最优方案提供更方便的解决思路。

[1] 刘向东, 习江鹏. 道路货物网络化运输的服务类别和发展模式[J]. 山东交通科技, 2011(5): 7-10. .

[2] AYED H, GALVEZ-FERNANDEZ C, HABBAS Z, et al. Solving time-dependent multimodal transport problems using a transfer graph model[J]. Computers & Industrial Engineering, 2011, 61(2): 391-401.

[3] 申勇, 杨兴宇, 黄文成. 我国铁路开行驮背式运输专列的SWOT-AHP分析[J]. 铁道经济研究, 2019, 147(1): 46-50.

[4] 冯芬玲, 余海军. 基于系统动力学与Logit模型的驮背运输运价研究[J]. 铁道科学与工程学报, 2018, 15(11): 266-273.

[5] 陈玥. 我国发展驮背运输的思考[J]. 铁道货运, 2017(5): 16-19.

[6] HAO C, YUE Y. Optimization on combination of transport routes and modes on dynamic programming for a container multimodal transport system [J]. Procedia Engineering, 2016, 137: 382-390.

[7] 吴必龙. 现有条件下我国铁路开展驮背式运输的技术条件研究[D]. 北京: 北京交通大学, 2015.

[8] 张磊. 关于道路运输基础设施建设的研究[J]. 中国商论, 2018, 744(5): 18-19.

[9] 美国交通研究委员会. 道路通行能力手册[M]. 北京：人民交通出版社. 2007.

[10] 李海鹰, 杨肇夏. 铁路货物运输组织模式改革方案研究[J]. 物流技术, 2010, 29(5): 27-29.

[11] 李臣, 何银川, 周炜, 等. 欧美驮背运输发展及对我国的启示[J]. 综合运输, 2017(11): 80-83.

[12] 钱海燕, 黄立雨. 汽车整车集装箱运输技术性及经济性分析[J]. 中国设备工程, 2017(10): 91-92.

[13] 陈雷. 低碳运输下公铁两网之间大宗货流转移及流量分配综合优化研究[D]. 北京: 北京交通大学, 2016.

[14] 潘立彦, 张大成. 改进Floyd算法在城市交通网络优化中的应用[J]. 物流技术, 2018, 37(11): 71-74. .

[15] 左秀峰, 沈万杰. 基于Floyd算法的多重最短路问题的改进算法[J]. 计算机科学, 2017, 44(5): 232-234.

Route Selection of Piggyback Transport Based on Traffic Network Graph Algorithms

AN Dong-dong1, WANG Hao-qing2, YI Hong-bo3, CHANG Chao4

（1. Sichuan Vocational and Technical College of Communications, Chengdu 611130, China;2. Sichuan Transportation Invetsment Industrial Co., Ltd. Chengdu 610023, China; 3. School of Transportation and logistics, Southwest Jiaotong University, Chengdu 611756, China; 4. Houma train depot, China Railway Taiyuan Group Co., Ltd. Houma 043000, China）

In this study, the development of the modern transport industry is analyzed, starting from the policy background and development status of piggyback transport. Global and cross-regional economic and trade activities are becoming more popular, and the need for a multimodal transport organization model is vital. In this study, a transportation network graph is used to simulate the connection between the transportation nodes and lines, and subsequently, the influence cost in the actual operation process is analyzed. Three parameters (time cost, expense cost, and traffic environment influence cost) are proposed. In the algorithm, the two modes of transportation were separated, and the cost of the first and last points and transshipment points were simulated in the model in a virtual line. The paper forming network graphics conforming to the traditional shortest path Floyd algorithm was determined, and computer programming was used to obtain the optimal combination of the results.

piggyback transport; route selection; traffic network diagram; Floyd algorithm

1672-4747（2020）02-0039-08

U294

A

10.3969/j.issn.1672-4747.2020.02.005

2019-06-13

安冬冬（1990—），女，回族，安徽凤阳人，讲师，主要从事交通运输规划与管理、交通安全方向研究，E-mail：andongdong.1990@163.com

安冬冬, 王浩庆, 易洪波, 等. 基于交通网络图算法的驮背运输路径选择研究[J]. 交通运输工程与信息学报, 2020, 18（2）：39-46.

（责任编辑：李愈）