大伙房水库供水量优化调度的水资源配置研究

彭 博

(辽宁省抚顺水文局，辽宁 抚顺 113015)

0 引 言

为满足水资源配置时下游水库的最小缺水量要求，一般在水库调度中寻求最佳的调度过程。在调配下游水量的过程中，通过水库的优化调度可有效的获取最优的调度过程线。当前，以遗传算法为代表的启发式优化算法和以动态规划为主的数学规划方法为优化算法的两种类型。随着计算规模的逐渐扩大及所求问题的复杂性和难度的提升，以“维数灾害”为标志的相关问题在动态规划等数学方法中相继出现。为解决此类问题，国内外研究者做了许多工作，提出了一系列的逐步优化、负荷分配等降维方法，这个问题随着计算机的普及和科技的发展得以缓解[1]。在处理数学规划方法的维数灾害问题时以随机生成个体为开始的启发式优化算法具有较好的实用性，对于该优化算法学者们开展了一些优化研究，如陈丹丹等为减少计算量和寻找最佳缝合线引入了图像拼接的方法；陈梁等运用贪婪算法调整了遗传算法的初始种群，但以上研究均未能有效处理运算过程中局部收敛的问题。我国学者崔志华提出了一种模拟人类社会群体行为的智能新型社会情感优化(SEOA)算法，具有更高的收敛效率。为求解水资源配置中最小缺水量问题引入社会情感算法，针对算法的收敛速度和个体生成问题，通过动态阈值和直线优化加以改进，然后以大伙房水库供水量优化调度为例探讨了模型的性能，在此基础上提出评价算法的有效度函数。

1 研究方法

1.1 模型的建立

1)目标函数。设定目标函数为水库下游缺水量在调度期内为最小，其表达式为：

(1)

式中：St、Nt为t时段的总供水量和总需水量，m3；T为调度段时期，月。

2)约束条件。水量平衡、水位、流量、调度期初和末控制水位的约束条件分别如下所示：

Vt+1=Vt+(Qt-Jt-Mt)·Tt

(2)

Zmin，t≤Zt≤Zmax，t

(3)

qmin，t≤qt

(4)

(5)

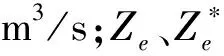
1.2 社会情感优化算法

人类社会中各个人的情绪特征和遭遇均存在较大差异，为获取不同的评价结果每个人采取的行为往往不同，将其表述为数学形式如下：

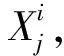
(6)

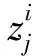
针对随机分布于整个搜索空间的初始种群，利用下式生成初始种群个体，即：

(7)

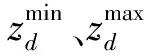
(8)

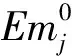
步骤二：社会评价值。确定社会评价值的重要依据为每个个体所处的位置，其中社会种群的历史最优评价值为计算确定的最优记录值，同理社会种群的历史最差评价值为记录的最劣值。个体的社会历史最优评价值记录为该个体的最优评价值，并将其记录于空间范围内相应的位置。将目标函数公式(1)利用罚函数法加以改造，从而构造社会评价数学模型，其表达式为：

(9)

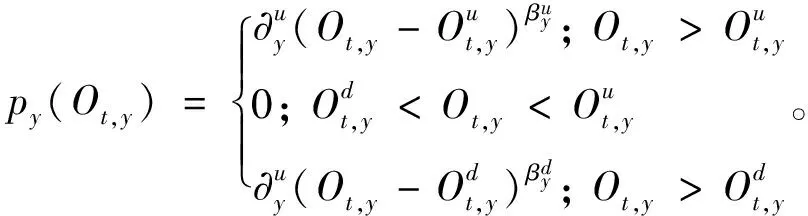
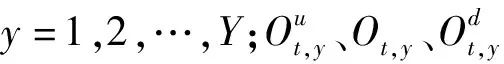
步骤三：更新情绪指数。根据下式更新个体的历史最优社会评价值与第i代种群的第j个当前社会社会评价值的水位点情绪指数，表达式为：

(10)

式中：Δ为情绪指数迭代参数。

步骤四：更新个体位置。每一个个体的情绪指数在初始种群中均为1，对于此次迭代运算个体认为正确，依据L个个体的最差社会评价值的教训作为学习方向，则原理L个个体的最差社会评价的位置即为更新方向，其数学表述为：

(11)

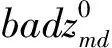
个体之间的情绪指数在迭代到第i代时发生了显著的改变，依据不同的个体类型、情绪阈值Th1、Th2与个体情绪指数之间的关系选取合适的更新策略。

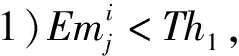
(12)

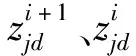
(13)

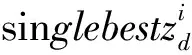
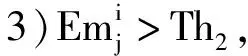
(14)

步骤五：终止判断。当达到终止条件时，则终止迭代运算，将种群最优解输出；反之，设i=i+1，重复以上步骤直至达到终止运算条件。

1.3 社会情感优化算法的改进

在运算过程中现有的智能优化算法通常存在一定的不足，如输出解局部最优、收敛速度不稳定等现象，社会情感算法作为新型智能优化法同样存在以上问题，为解决此问题考虑从收敛速度和初始种群生成的角度改进SEOA算法。

1.3.1 初始种群的直线优化

在生成初始种群时基本的智能算法往往偏向于随机，该过程显著影响着模型的收敛速度，对此提出直线优化过程解决初始个体生成存在的不足。采用上、下限平均值在相同的位置上生成初始个体，该过程即为直线优化初始种群，以数学的形式表述为：

(15)

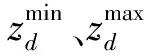
为了更加有利于全局收敛和最优解的收敛，在迭代运算过程中按照式(15)生成的初始个体可实现两边扩散运算。

1.3.2 情绪阈值的动态设计

在运算过程中基本算法的情绪阈值不产生变化，具有过程简单、运算方便等优点，然而收敛速度在实际操作时较慢，为解决收敛速度不足的问题提出动态设计情绪阈值的方法。

为了使种群个体能够更有效的选择决策设计了情绪阈值的动态操作，对个体的情绪指数在第i次迭代运算时排序，设Th1、Th2为个体排序排序[j/3]、[2j/3]时的情绪值，如式(16)，由此实现个体的动态选择，社会情态优化算法改进前、后的对比，如图1所示。

(16)

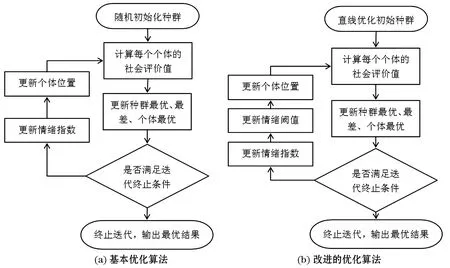
图1 社会情态优化算法改进前后的对比图

1.3.3 求解步骤

水库调度缺水量最小问题利用改进的社会感情优化算法处理，其详细流程为：

步骤一：初始化处理。初始参数的确定包括差个体数L、学习因子b1、b2、b3、情绪迭代参数、情绪指数初始阈值Th1、Th2、最大迭代次数kmax和种群规模H等。

设定调度决策变量为水库的水位，采用实数编码算法的个体。针对水库调度关于时段T的最小化的处理，利用公式(6)对个体j在第i代种群中编码。水库调度中的下限、上限水位设定为各个搜索维度的上下限，必须在上下限之间完成初始的生产及相关运算，初始个体的生成利用式(15)完成，采用约束条件公式(5)设定水库调度期初、末水位，利用公式(8)设定初始情绪指数值为1。

步骤二：求解社会评价值。在水库调度过程中通常存在非线性约束条件，因此各个社会评价值利用罚函数法和公式(9)确定。记录所有利用的社会评价值和每一次运算的目标函数值，对以上调度过程曲线记录。

步骤三：更新情绪指数和阈值。对当前社会评价值是否为最优判断，对个体情绪值利用公式(10)更新；然后依据大小排序所有个体的情绪值，对个体情绪阈值利用公式(16)更新。

步骤四：更新个体位置。对个体位置按照记录的3个社会评价值和公式(11)-(14)更新，更新后的个体若低于下限水位或超过上限水位，则取下限或上限水位。

步骤五：终止判断。以最大迭代次数kmax为标准判断迭代次数是否达到终止运算条件，若未达到kmax，则设k=k+1重复以上计算流程直至满足终止要求，输出缺水量最小和水位最优调节过程。

2 实例分析

2.1 工程概况

当前，大辽河、太子河和浑河等流域的水生态环境持续恶化，地面沉降、水质污染及地下水超采等问题十分突出，在缓解太子河、浑河等地区的水资源矛盾和改善水体环境，促进老工业基地振兴发展和该地区水资源合理配置等方面，大伙房水库发挥着巨大的作用。文章以辽东地区新宾县和桓仁县境内的大伙房水库输水工程为例，其主要目的为满足辽中地区城市群设计水平年工业用水和城市生活用水。山区性河流为输水工程调出区的典型特征，流域水资源丰富具备向外流域调水的条件，水资源平均占有量为69375m3/hm2。桓仁水库坝下凤鸣电站库区为该大型调水工程的取水口位置，经大伙房水库调节后向盘锦、辽阳、营口、鞍山、沈阳和抚顺等城市提供工业和生活用水，年均调水量17.88亿m3，设计引水流量70m3/s。由于地区缺水和用水供给紧张，现规划计算2022年大伙房水库的调度方案，概化的供水系统结构如图2所示。

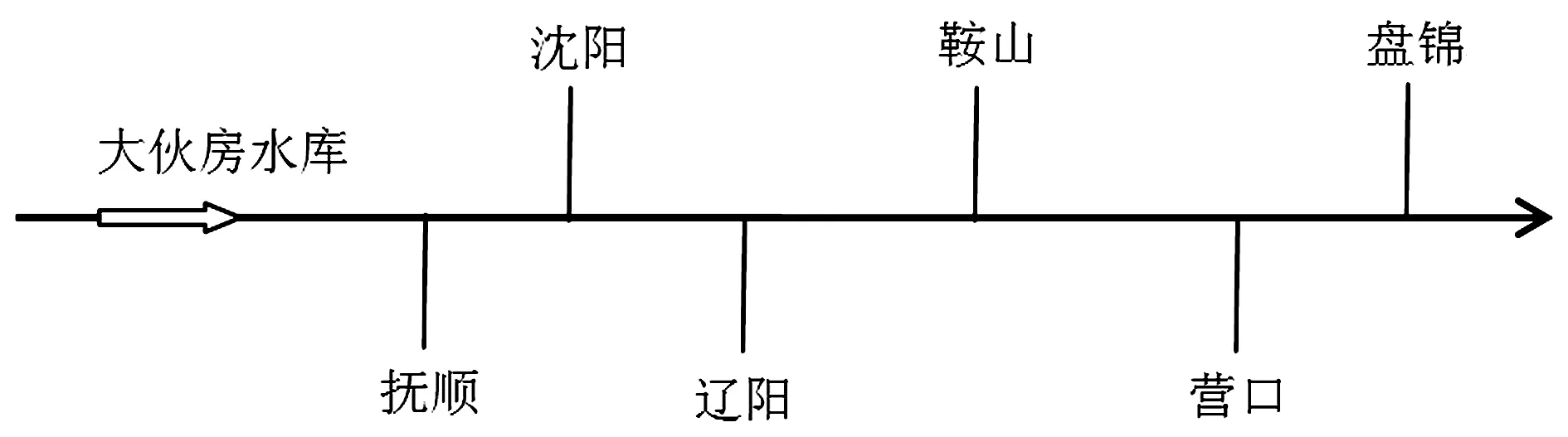
图2 大伙房水库供水系统概化图

2.2 需水量预测

将各地区2022年的需水量利用回归分析法预测，结果如表1所示。

2.3 优化配置结果

对大伙房水库6个供水地区2020年的用水量月分配情况利用构建的模型进行求解，结果如表2所示。

表1 大伙房水库下游2022年需水量预测 105m3

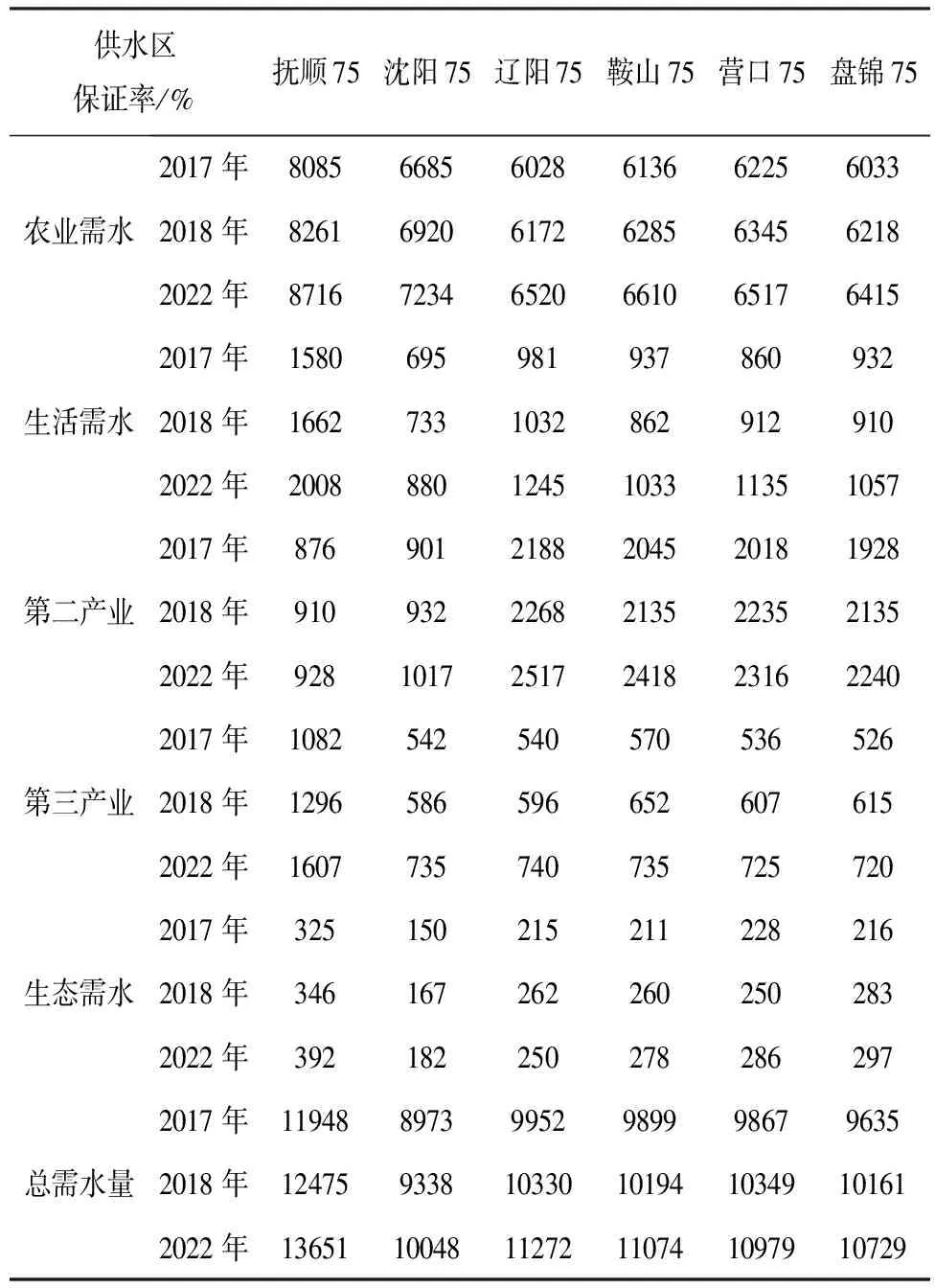
供水区保证率/%抚顺75沈阳75辽阳75鞍山75营口75盘锦75农业需水2017年8085668560286136622560332018年8261692061726285634562182022年871672346520661065176415生活需水2017年15806959819378609322018年166273310328629129102022年20088801245103311351057第二产业2017年87690121882045201819282018年91093222682135223521352022年92810172517241823162240第三产业2017年10825425405705365262018年12965865966526076152022年1607735740735725720生态需水2017年3251502152112282162018年3461672622602502832022年392182250278286297总需水量2017年11948897399529899986796352018年124759338103301019410349101612022年136511004811272110741097910729

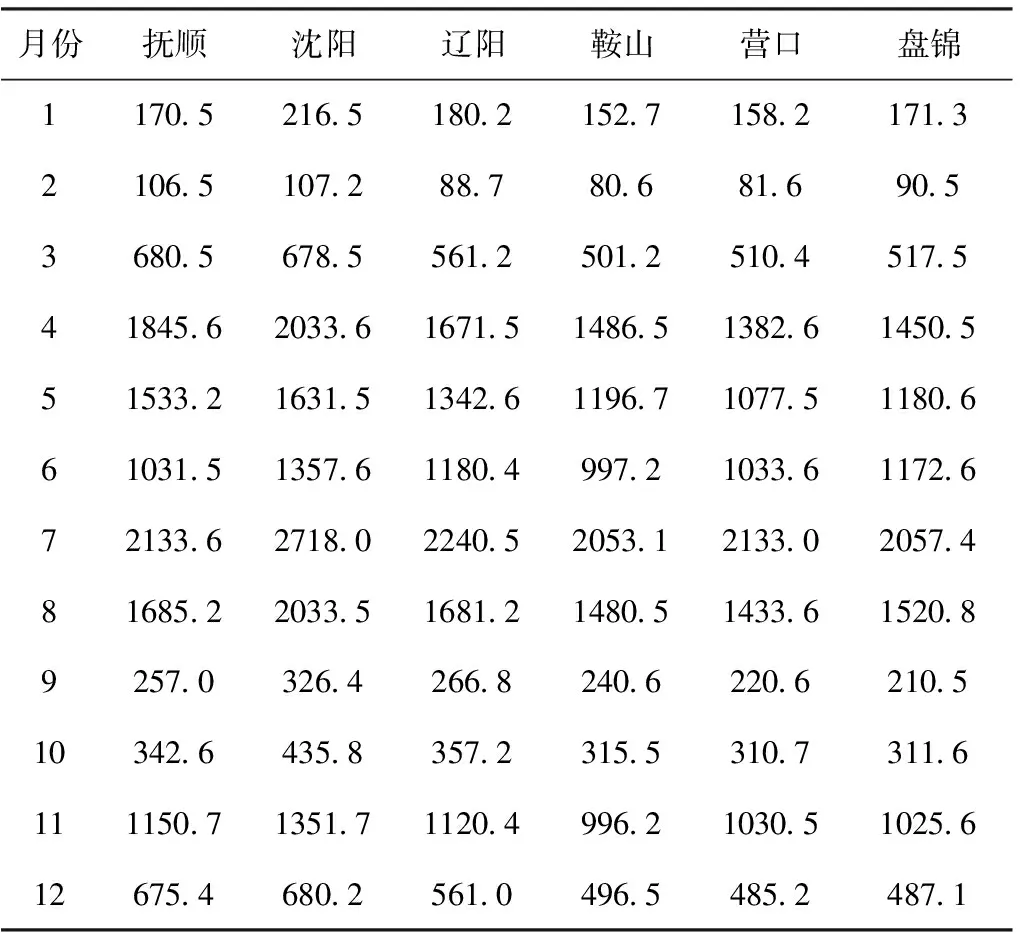
表2 大伙房水库6个供水地区的用水量月分配情况 105m3

库水位调度实际情况与调度曲线利用折线图表示较为接近，因此采用该方法展示改进的SEOA算法库水位调度情况，如图3所示。

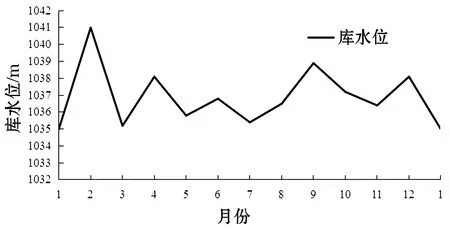
图3 大伙房水库2022年水位调度预测曲线

2.4 算法性能分析

对模型运用改进的SEOA、基本SEOA和遗传算法求解，在精度相同的情况下利用动态规划算法求解，算法性能的判别利用指标数η描述，其表达式为：

(17)

式中：T、Tz为计算总时刻数和完成所有计算的时间，min；Jt、Ut为最小缺水量同等精度下的精确解和t时刻所得的最小缺水量，m3；kn为修正的迭代次数参数，n为1-10、10-100、>100时取1.1、1.3、1.5；n为迭代次数。

分段时长和初始个体精度相同为该函数使用的基本前提，在该条件下方可用于对比分析。采用试算法，经多次调整和试算确定的各参数最终值如表3所示。

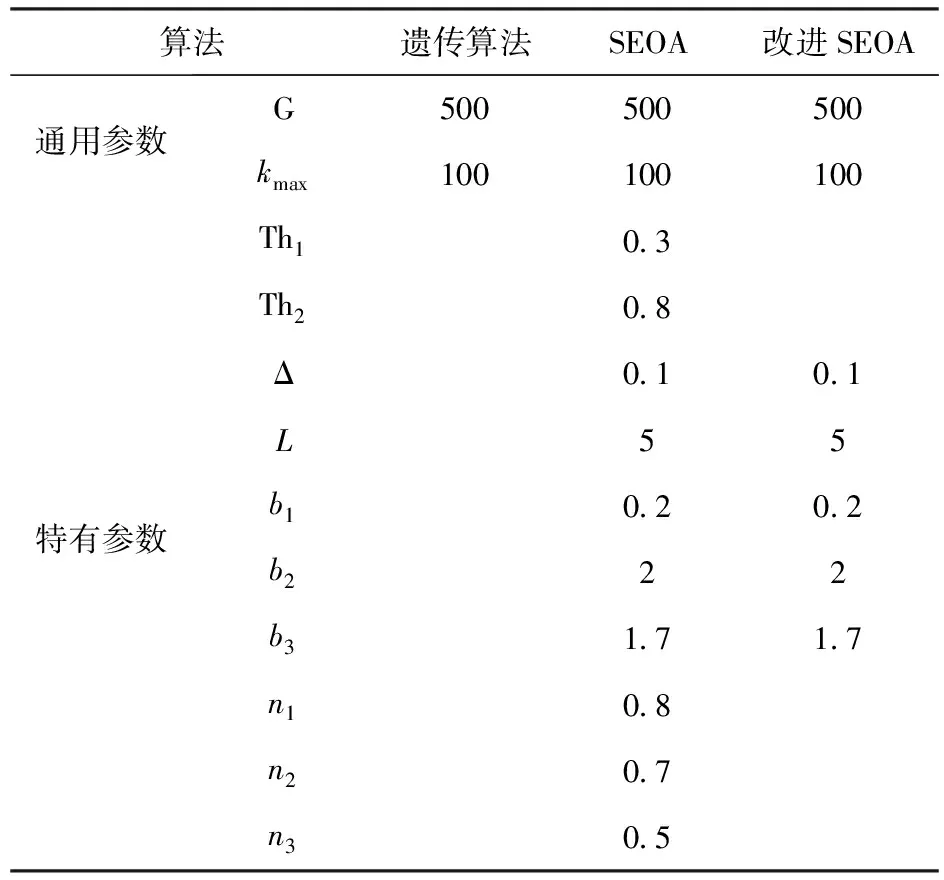
表3 不同算法的参数取值

为保证计算结果的代表性对每种算法独立运算20次，将评价指标设定为统计的耗时、标准差、平均值和最优值。数据的运算空间为window7操作系统，各评价因子值关于以上3种不同算法的结果如表4所示。

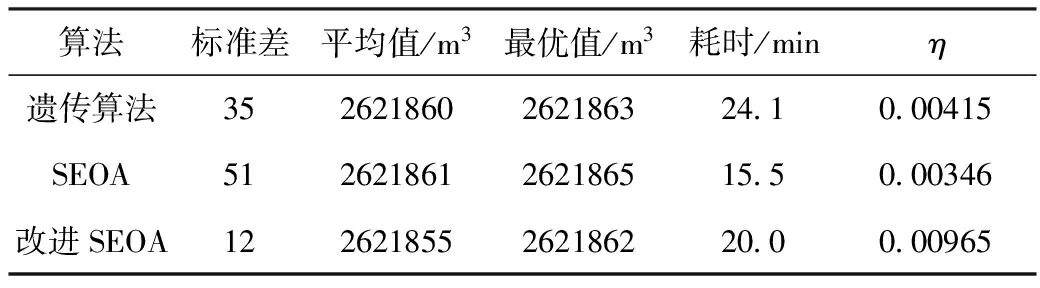
表4 各项评价因子关于3种算法的计算值

遗传算法和SEOA算法等智能算法较传统的以动态规划为代表的数学规划法，能够较好的解决维数灾害的难题。根据本次运算结果，设定迭代次数为100的条件下，SEOA算法的运算结果与精确解非常接近，改进SEOA算法具有一定的代表性，对于动态规划获取的精确解该算法具有较好的收敛性。通过比较分析3种不同算法的计算结果，有效度函数值最高的为改进的SEOA算法，较其它两种算法在精度相同的情况下改进SEOA具有一定的优势，且算法的性能可通过η值来体现。另外，对个体利用遗传算法求解时，其收敛速度要高于普通的SEOA法，通过改进情绪阈值和初始个体可大大增加收敛速度，同时计算结果更加趋近于精确解。

3 结 论

文章对大伙房水库地区的缺水量最小问题利用SEOS算法进行求解，从情绪阈值和生成初始种群的角度改进了传统算法，得出的主要结论如下：

1)新型智能的SEOA算法能够较好的处理复杂问题求解时存在的维数灾害问题，较其他传统启发式算法其初期收敛速度保持一致，且具有较强的最优解搜索能力。

2)在生成初始种群时改进的SEOA算法存在明显的优势，在迭代次数相同的条件下通过更新情绪阈值，具有更高的获取全局最优解的概率。其收敛速度较普通的SEOA法明显提升，计算精度和运算速度更高。

3)通过水库蓄水容量曲线和回归分析法的求解，对浑河、太子河流域6个地区2022年需水量进行了准确预测，获取了6个地区的水资源优化配置和库水位最小缺水量调度曲线，在实际工程中具有较强的适用性月可靠性。