基于基尼系数法的灌区农户间水权分配研究

管新建，黄安齐，张文鸽，孟 钰

(1. 郑州大学水利科学与工程学院，河南 郑州 450001；2. 黄河水利委员会黄河水利科学研究院，河南 郑州 450003)

0 引 言

随着人口的增长和社会经济的发展，人们对水资源的需求量不断上升，且水资源污染、浪费现象严重，水资源短缺已成为我国经济发展的一大障碍[1]。农业作为我国用水大户，用水方式较为粗犷，水资源浪费现象严重，其主要原因是水权的缺位。通过建立和完善水权制度，实施水权交易挖掘农业节水潜力是解决我国水资源短缺的有效途径[2]。目前国内关于初始水权分配的研究已取得了一些成果。肖淳[3]提出了基于水权分配原则友好度函数的水权分配模型，并将此模型运用到湖北省环河流域初始水权分配中，通过混沌优化算法对函数求解，实现了流域水权在行政区之间的分配。褚钰[4]考虑用水主体对水权分配的满意程度并结合初始水权分配原则，构建了清漳河流域水资源优化配置模型。王宗志[5]根据水资源量质统一的属性，建立了流域二维水权分配模型，满足了初始水权和初始排污权统一分配的要求。胡洁[6]利用多层次多目标模糊优选方法对流域初始水权进行分配，分配结果较其他分配模式更具公平性、高效性及合理性。吴振针[7]对初始水权分配指标体系中选取指标的相关性和权重确定的主观性问题，将主成分分析法应用到区域初始水权中，借助博弈论对指标进行综合集成赋权，结果表明该方法具有一定的合理性。张璇[8]提出了基于相对关联度的流域初始水权分配群决策模型，分配结果表明该模型在解决流域初始水权分配存在的多目标性、不确定性及复杂性等问题上有一定的可行性。但以上研究主要集中在较高层次的初始水权分配，且水权分配理论及方法多集中于以流域为单元的研究机制上，如何实现较低层次的农业水权在微观主体间(农户或农民用水者协会)分配的研究较少。鉴于基尼系数法在评价资源合理性配置方面有较为广泛的应用，本文以灌区农户间水权分配为研究对象，采用基尼系数作为衡量水权分配的公平性测度，通过合理选取指标，构建基于基尼系数最小化的灌区农户间水权分配模型，研究成果可为区域单元农业水权分配提供新的思路与方法。

1 水权分配总量及分配思路

由于农业灌溉用水量较大，本文涉及的农业水权仅指灌溉水权。结合灌区水权分配实际情况，将农业水权界定到灌区干渠上开口的直口渠，以直口渠为单元，通过本文建立的模型将水权分配到农户。

1.1 直口渠农业水权分配总量的确定

灌区直口渠水权的确定一般以多年平均用水为基础，扣除各节水措施下的节约水量，即为直口渠的水权分配总量。灌区节水工程一般包括畦田改造、渠道衬砌、畦灌改地下水滴灌，所节约的水量为各项节水措施所节约的总水量，各节水措施的节水计算公式如下。

(1)渠道衬砌。渠道衬砌的节水量主要为渠道衬砌实施前后输水损失量的变化，节水量为渠道衬砌实施前后输水损失量的差值，即

ΔW衬=ΔW衬前-ΔW衬后

(1)

ΔW衬前=W(1-η)

(2)

ΔW衬后=W′(1-η′)

(3)

式中；ΔW衬为渠道衬砌节水量，万m3；ΔW衬前为渠道衬砌前的输水损失量；ΔW衬后为渠道衬砌后的输水损失量；η、η′为渠道衬砌前后的直口渠渠道水利用系数；W、W′为渠道衬砌前后的引水量。

(2)畦田改造。畦田改造的节水量主要为畦田改造前后田间灌溉水量的变化，即

ΔW畦田=W畦前-W畦后

(4)

式中：ΔW畦田为畦田改造节水量；W畦前、W畦后为畦田改造前后田间的灌水量。

(3)滴灌。滴灌节水量为畦灌改造为滴灌前后渠道引水量的差值，即

ΔW滴=W滴前-W滴后

(5)

式中：ΔW滴为滴灌节水量；W滴前、W滴后为改造前后直口渠渠首的引水量。

(4)节约的总水量为：

ΔW总=ΔW衬+ΔW畦田+ΔW滴

(6)

(5)区域单元确权总水量为：

W权=W平-ΔW总

(7)

式中：W平为区域单元多年实际平均用水量。

1.2 分配思路

农业水权分配主要从农户人口和灌溉面积两方面考虑：

(1)灌溉面积。现状农业水权分配模式以农户灌溉面积进行水权分配，农户拥有的灌溉面积越多，其灌溉需水量也就越大，相应地分得的水权也就越多，按灌溉面积进行水权分配主要体现了各农户用水需求的差异性，即农户i分得的水权为：

Wi=qAi

(8)

(9)

式中：Wi为农户i的分配水权；q为水权分配定额；A为农户i的灌溉面积；A总为区域单元所有农户进行确权灌溉面积；W总为区域单元分配水权。

(2)农户人口。水资源作为全社会的公共资源，所有人对水资源的使用权和所有权都是相同的，在进行水权分配时应充分考虑人口因素。按人口进行水权分配主要体现了水权分配的公平性原则，农户人口越多，分配的水权也就越多。

2 基于基尼系数农户间农业水权分配模型的构建

针对灌区现状水权分配模式未能考虑农户人口因素，由于农户人口和灌溉面积的非对称性，各农户人均灌溉面积差别较大，现状水权分配模式导致水权分配不公平。基于此，本文运用基尼系数理论研究灌区农户人口和灌溉面积之间的分布关系，构建基于基尼系数最小化为目标函数的水权分配模型，对农户现状人均灌溉面积进行均衡，进而对农户进行水权分配的灌溉面积进行调整，在给定的约束条件下探寻最为公平的水权分配方案。

2.1 基尼系数

基尼系数(洛伦兹系数)最初为意大利数学家基尼提出，用来评价区域居民收入和财富分配的不公平程度[10]，表示财富在居民收入之间分配越不公平，能够较为直观地反映收入分配的均衡程度。现被广泛应用到污染物总量分配、资源配置公平性评价、水资源利用[11]等领域。洛伦兹曲线见图1。

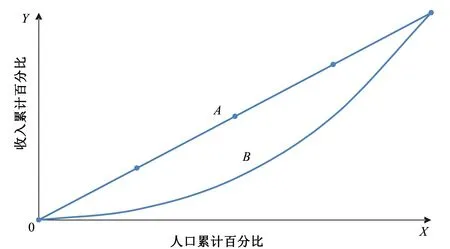
图1 人口-收入洛伦兹曲线Fig.1 Population-income Lorenz curve

图中OX为人口累计所占的百分比例，OY表示收入累计所占的比例，实际分配曲线表示为收入情况的洛伦兹曲线，绝对平等分曲线表示为收入绝对平等。A表示实际分配曲线与绝对平等分曲线围成的面积，B为实际分配曲线与OY围成的面积。A与A+B的比值即为基尼系数，基尼系数计算方法较多，常用的计算方法为梯形面积法[12,13]，即：

(10)

式中：Gj为指标j下的基尼系数；Xji为评价对象i时的指标j的累计百分比；Yi为评价对象i时累计分配百分比。

基尼系数越小表示收入分配越平均，越大表示收入分配差距悬殊，计算出的基尼系数取值范围为[0,1]，基尼系数为0时表示收入分配绝对平均，基尼系数的国际参照标准见表1。

表1 基尼系数评价标准Tab.1 Gini coefficient evaluation standard

由于经济社会的发展，人均收入不可能达到完全平均，基尼系数在0.2～0.4是正常的，但很少能达到0～0.2的标准。但由于水资源作为公共资源，所有人对水资源都有同等使用和发展的权利，因此认为基尼系数趋于0是合理的[14]。

2.2 水权分配模型构建

以农户人口为评价指标，灌溉面积为匹配对象，由于基尼系数越小表示分配的结果越公平，构建如下目标函数：

minGini

(11)

(12)

(13)

约束条件主要从以下几个方面进行考虑：

(1)公平性约束条件：对农户人均灌溉面积超出区域单元平均人均灌溉面积的进行削减，不足的进行补偿，即：

(14)

(2)基本用水保障约束条件：为保障灌区粮食生产安全且不影响农户种植积极性，不能对农户的人均灌溉面积进行大幅度削减，且对农户人均灌溉面积超出平均水平越多，其削减补偿程度越多：

(15)

式中：p为削减比例，由区域对公平原则的重视程度而定，本文取0.3。

(3)排序约束条件。均衡过后各农户在洛伦兹曲线的相对位置不发生改变，各农户的人均灌溉面积大小排序仍满足均衡前的排序，确保农户间水权分配的公平性，即：

xi-1≤xi≤xi+1

(17)

(4)灌溉面积约束条件。均衡前后区域单元所有农户进行水权分配的灌溉面积不发生改变，即：

(18)

式中：pi为农户i的人口；A总为区域单元所有农户进行水权分配灌溉面积。

(5)指标现状基尼系数约束条件。均衡过后的人均灌溉面积，计算其基尼系数应当小于现状人均灌溉面积的基尼系数，确保分配方案整体的公平性，即：

(19)

(6)非负性约束条件。各农户均衡后的人均灌溉面积不能为负数，即：

xi>0

(20)

2.3 农户水权分配模型

根据均衡过后的各农户的人均灌溉面积确定其分配水权，农户i分得水权Wi为：

(21)

式中：W总为区域单元分配的总水权量；其他符号同上。

3 实例分析

3.1 研究区概况

乌兰布和灌域位于巴彦淖尔西南部，乌兰布和沙漠东缘，东经106°09′～107°10′，北纬40°09′～40°57′，是内蒙古河套灌区的5个灌域之一。2016-2017年，以乌兰布和灌域沈乌干渠开展了引黄灌溉水权确权登记与用水指标细化工作，将引黄水资源使用权细化到终端用水户。本次确权工作以2012年为基准年，开展以乌兰布和灌域内国管(干、分干渠)渠道上开口的直口渠为单元，统计直口渠上农户灌溉面积、农业人口、种植结构等基本信息，确权范围为2012年在国管渠道上开口的直口渠控制的灌溉范围。本次确权涉及到直口渠411条，5个乡镇、5个国营农场15 008个用水户。沈乌干渠根据灌溉渠系分布可分为一干渠灌域和东风分干渠灌域两大区域，现以一干渠上的直口渠牧业队(4)的8户农户为例，进行引黄灌溉农业水权分配。

3.2 直口渠水权的确定

根据收集的资料，该直口渠近五年实际用水量见表2。

表2 渠系近五年实际用水量Tab.2 Actual water consumption of canal system in recent five years

目前该直口渠节水措施进行了畦田改造，畦田改造前后田间灌水量的差值为0.73 万m3，结合公式(2)、(4)、(5)计算得到直口渠牧业队(4)的确权水量为1.70 万m3。

3.3 农户水权分配结果

按照基尼系数的计算公式，将农户的人口及对应的灌溉面积数据按照人均灌溉面积由小到大进行排列，计算过程见表3。

表3 农户现状人口-灌溉面积基尼系数计算结果Tab.3 Calculation results of Gini coefficient of current population of farmers-irrigation area

计算出的基尼系数为0.196 8，根据分配模型及设定的约束条件，采用遗传优化算法对模型进行求解，对直口渠牧业队(4)上8户农户的人均灌溉面积进行均衡，均衡后的农户人均灌溉面积见表4。

表4 模型分配的农户人口-灌溉面积基尼系数计算结果Tab.4 Calculation results of Gini coefficient of the population of farmers - irrigation area allocated by model

根据表4中农户均衡过后的人均灌溉面积，计算其基尼系数为0.128 9，结合公式(11)，确定各农户的分配水权。由图2分配结果知：农户1、2、3、4的现状人均灌溉面积均小于平均人均灌溉面积0.1 hm2/人，经过目标函数对人均灌溉面积均衡后，模型分配水权大于现状分配水权；农户5、6、7、8的现状人均灌溉面积大于平均标准，因此模型分配水权小于现状分配水权，分配结果证明了运用该模型进行水权分配的合理性。基于公平原则下，农户1、2、3、4的模型分配水权大于现状分配水权，总量为972 m2，该部分结余的水权可视为公平原则下的农业灌溉节水潜力；对于农户5、6、7、8，其模型分配水权小于现状分配水权，农户可通过调整种植结构及改进灌溉技术压缩亩均用水量。模型分配结果能够促进区域农业节水，同时也可为区域农业节水潜力评估提供新的思路。

图2 模型分配水权与现状分配水权对比图Fig.2 Comparison diagram of the volume of water right allocated between by model and by current situation

4 结 语

水权分配是进行水权交易的前提，因此有必要确保初始水权分配的公平性。本文以河套灌区乌兰布和灌域-沈乌干渠推进的水权分配试点为例，提出了基于农户人口和灌溉面积的农业水权分配方法，充分考虑了农户人口因素，体现了水权分配的公平性原则。分配方案的基尼系数由现状分配模式的0.196 8降低到0.128 9，分配结果更具公平性，能够为其他地区开展农业水权分配工作提供一定借鉴和参考。