浮筒式升降闸门水力性能数值模拟

韩 宇，忻佳丽，孙小雨，周炳旭，龙廷源，唐良川

(中国农业大学水利与土木工程学院，北京 100083)

0 引 言

灌区作为农业生产的主要阵地，在灌区实现精准灌溉对于国内水资源缺乏地区十分重要，而实现精准灌溉的重要手段之一就是灌区量水技术[1]。现今各灌区的主要渠道基本都设置了能满足各种量水需要的量水设备，如各式量水堰、量水槽、量水槛等[2]。

但是，受末级渠道所处位置的影响，末级渠道坡降缓、其渠道水流量小而波动大、泥沙含量较高，这导致一般的量水设施难以发挥作用。因此，有必要研究设计一个适用于末级渠道的量水装置。目前，应用于末级渠道的量水技术有机翼型量水槽量水[3-5]、斜坎量水堰量水[6]等，而在这众多量水技术中，闸门量水技术具有经济和简便的特点。

在闸门量水技术上，众多学者都进行了自己的改良与创新。赵登明等[7]提出一种新型节水孔口闸门，该闸门具有分水、量水、控水等多种功能。Vatankhah等[8]设计了一种半圆形翻板闸门，可用于测量水平圆形渠道自由出流状态下的流量，并能有效防止测量装置上游的泥沙沉积。潘志宝等[9]研制了一种可量控水的宽顶堰平板压差式量水闸门，适用于平原灌区中的淹没出流情况。现今，灌区要求量水建筑物具备控水能力，因此各式量水闸门的研究逐渐加快，但总体上而言，测控一体化闸门的研究与应用还不够深入。

随着计算机技术的发展，很多学者开始采用数值模拟对物理模型进行仿真研究。数值模拟成本低、模拟速度快、准确率高，这使得数值仿真技术持续快速发展。Aydin等[10]基于FLUENT软件运用VOF模型对三角形迷宫侧堰进行模拟，发现该模型能很好地描述其流动特性。Mohammadpour等[11]运用数值模拟来研究多孔宽顶堰，结果表明该数值模型能够较为准确地分析堰周围的流动模式。Xiao等[12]对便携式短喉水槽进行了数值分析，发现得到的各项参数与试验十分吻合。因此，数值分析结合物理模型试验能够有效地确定各种量水设施的水力特性。

本文设计浮筒式升降闸门，分析浮筒式升降闸门测流原理及计算公式，并结合物理模型试验结果探讨了测流公式的精度，以优化浮筒式升降闸门的结构设计，为其实际应用提供理论依据。此外，本文基于物理模型试验结果，采用VOF模型对浮筒式升降闸门水力特性进行研究，将模拟结果与试验结果进行对比，分析了浮筒式升降闸门前后水流流速结构、水面线变化情况及相关水力特性。

1 浮筒式升降闸门结构及模型试验

1.1 浮筒式升降闸门结构

浮筒式升降闸门造价低、结构简单，适用于量控末级渠道水[13]。如图1、图2、图3所示，浮筒式升降闸门由一个锥形的浮筒闸体以及闸门孔板构成。

图1 浮筒闸体Fig.1 Float

图2 孔板Fig.2 Orifice-plate

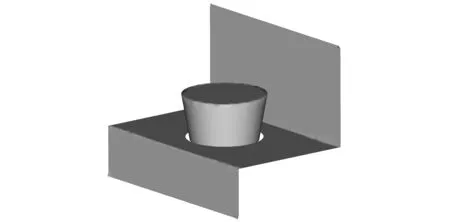
图3 浮筒式升降闸门整体Fig.3 The whole float lift gate

浮筒式闸体结构设计参数包括上底面半径r1、高度h和锥角 ，闸门孔板结构设计参数包括孔口直径D、孔板高H、孔板宽B、孔板长L。在浮筒式升降闸门中，闸门孔板是重要的组成部分。闸门使用时的过水面积取决于浮筒式闸体与孔板之间的间隙的大小，所以为了准确测量过水流量，需要对闸门孔板进行进一步的设计。本文根据已设计的浮筒式闸体的体型来确定闸门孔板的尺寸。浮筒闸体与孔板的具体参数值见表1、表2。

表1 浮筒闸体参数Tab.1 Float parameters

表2 孔板参数Tab.2 Orifice-plate parameters

1.2 浮筒式升降闸门测流原理

闸门的开度e定义为闸门提升的高度，当闸门完全堵住孔板时，开度e为0，此时无水流通过。当末级渠道需要引水时，使用外部升降装置来提升浮筒式的闸体，使渠道上游的水流从闸体与孔板之间的空隙中流过。通过改变提升的高度来改变闸体与孔板之间的空隙大小以控制过流的水量，当水流通过时能在闸门前保持稳定的水位，使流量与上游来流形成单一稳定的水位-流量关系，从而实现测流，测流原理如如图4所示。

图4 浮筒式升降闸门测流示意图Fig.4 Flow measurement diagram of float lift gate 注：R为闸孔的半径；r1、r2为浮筒上、下底面的半径；e为浮筒式升降闸门的开度；H1、H2为闸前和闸后水位。

1.3 试验设计

模型试验在中国农业大学水力公共试验大厅的明渠装置上进行，矩形渠道长6 m，宽0.8 m，高0.6 m，渠道通过供水管连接实现内部水体的循环流动。试验设计5种流量工况(7.22、7.78、8.89、9.44、10.56 L/s)，分别对3种闸门开度(85、69、49 mm)进行量水试验研究，每种工况下均为自由出流。试验中用水位测针分别测量不同工况下闸门上游距闸门处1 m的测点水位以及闸门下游距闸门4 m处的水位。进而进一步讨论水位—流量关系。试验装置安装效果如图5所示。

1.4 流量公式推导

简单实用的流量公式有助于量水设备在灌区的应用。浮筒式升降闸门的过流流量主要受到渠道几何参数、闸门开度、上游水位的影响。本文利用量纲一致性原理对闸门的过流流量公式进行推导[14]。

函数关系式：

f=(Q,H0,b,e,v,g,μ,ρ,σ)

(1)

式中：Q为过流流量，m3/s；H0为上游水深，m；b为渠道宽度，m；e为闸门开度，m；v为流速，m/s；g为当地重力加速度，m/s2；μ为动力黏度，kg/(m·s)；ρ为密度，kg/m3；σ为液体表面张力系数，N/m。

从式(1)的9个物理量中选取3个物理量ρ、g、H0作为基本物理量，利用π定理，确定6个无量纲数：

(2)

根据量纲一致性原理，计算式(2)中各指数，然后代入式(1)得到新的关系式：

(3)

(4)

令式(4)等号右边为流量系数u，利用试验数据对u与b/H0、e/H0、Fr进行拟合分析从而得到浮筒式升降闸门流量公式：

(5)

化简后得：

(6)

2 数值模型控制方程及参数定量

2.1 控制方程与参数

(1)连续性方程：

(7)

式中：ρ为密度；ui为坐标分量；t为时间。

(2)动量方程：

(8)

式中：ρ为密度；ui、uj为速度分量；xi、xj为坐标分量；t为时间；p为压力；μ为动力黏滞系数；S为广义源项。

(3)湍流模型[15]。 RNGk-ε模型是对标准k-ε模型的改进，对k-ε方程进行了修正，在ε方程中加入一个主流时均应变率，RNGk-ε模型方程分别为：

(9)

(10)

计算η：

(11)

式中：主流时均应变率Eij=0.5(∂ui/∂xj+∂uj/∂xi)。

2.2 模型描述与网格划分

试验模型由渠道与浮筒式升降闸门两部分组成，为了使模拟过程中水流在流入闸门前能达到一个平稳的状态，本文取用于仿真的模型渠道长19 m，宽0.8 m，深0.6 m。闸门安放在距离渠道入口6m处，以保证闸门附近的水流流态稳定。坐标原点取在渠道进口断面中心处，渠道顺水流方向为x轴正方向，渠宽沿z轴关于坐标原点对称，从渠底到渠顶为y轴正方向。由于在浮筒式升降闸门附近水力条件复杂且该处为重点观察对象，因此在闸门段采用非结构网格、渠道段采用结构网格进行划分，如图8所示，这样可以在保证精度的前提下减少运算时间；并且着重在结构复杂的重要过流区域——孔板的圆孔以及浮筒闸体靠近孔板位置附近进行网格局部加密处理，如图6、图7所示，最后网格总数约为2.1×106个。

图6 浮筒闸体网格划分Fig.6 Grid division of float

图7 孔板网格划分Fig.7 Grid division of orifice-plate

图8 网格划分整体示意图Fig.8 Schematic diagram of overall grid division

2.3 计算求解

(1)边界条件。将渠道的入口下部定义为水流速度入口，上部定义为空气压力进口，根据试验中实测流量给定一系列的速度值，水流流动方向与边界垂直。渠道顶部也设置为空气压力进口。压力出口边界有利于解决出口回流收敛的问题，所以将渠道的出口定义为压力出口。渠道整个底部、边壁、孔板以及浮筒闸体定义为固体边壁，给定无滑移边界条件。使用瞬态求解，通过VOF模型进行迭代，追踪自由液面，每个单元中水和气体体积分数为1，即

aw+aa=1

(12)

式中：aw为计算域中水体积分数；aa为计算域中气体体积分数。

又有连续性方程：

(13)

式中：aw为计算域中水体积分数；t为时间；ui为速度分量；xi为坐标分量。通过以上两个方程可得水的体积分数aw与空气体积分数aa，从而可以计算得到自由液面的位置。

(2)计算方法。本文采用湍流模型进行数值模拟，同时用VOF模型追踪自由液面，并使用隐式计算方法以及瞬态PISO 算法求解;对流项使用二阶迎风格式, 最小步长设为10-6s；对出口质量流量进行监测，当其值接近于0且基本保持不变，认为计算收敛。

3 结果分析

3.1 模型验证

控制断面选取距离闸门1m的截面，此处水深较为稳定。将实测流量与模拟流量、实测水深和模拟水深进行对比分析，结果如图9、图10所示。可以得出模拟水深与实测水深的最大相对误差为1.9%，随着开度的减小，流量对比误差也随之减小。模拟流量与实测流量之间最大相对误差为7.96%，符合灌区测流的要求。因此，本文建立的浮筒式升降闸门的数值模型无论是在计算方式的选择还是模型网格的划分上都具有一定的准确性，模拟结果准确可靠，因此利用数值模拟的相关方法来对浮筒式升降闸门的水力特性进行研究是可行的。

图9 实测水深与模拟水深对比Fig.9 Contrast between measured depth and simulated depth

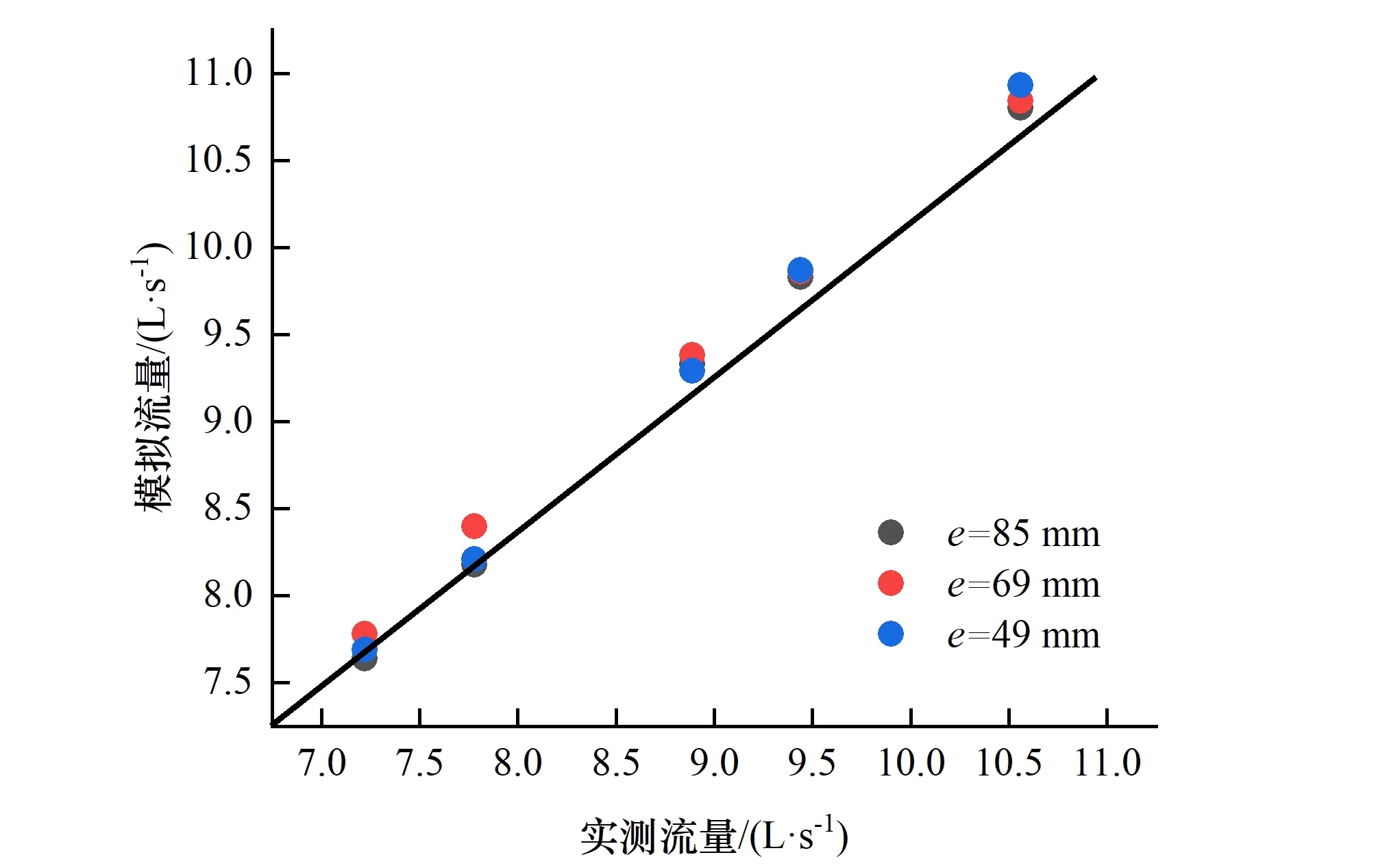
图10 实测流量与模拟流量对比Fig.10 Contrast between measured flow and simulated flow

3.2 水面线

在本次研究中，水面线的影响因素主要有闸门开度以及过流流量等。选取开度为85 mm时的闸门模型，在不同的流量工况下对模型在z=0位置上的各处水位进行研究，即可得浮筒式升降闸门及其上下游一定范围内的水面线变化情况。由图11可知，在闸门前一段距离内水面较平稳，在闸门前侧挡板位置附近受挡板影响，水面先发生微小的下降，后又迅速恢复。而在渠道的下游，由于环状过流面中垂直下落的水流对下游造成冲击，因此在下游环状过流面投影附近一定范围内，水流的流态十分复杂。如图12所示(图中Phase2为空气相在各处的含量)，在渠道下游一段距离内由于受到水流冲击，水面产生波动，而在渠道下游x>7 m的位置，水面逐渐恢复平稳。总体上看，随着渠道中流量的增大，各处水位升高。

图11 水面线Fig.11 The water surface line

3.3 流速分布

分析开度为85 mm，流量为7.78 L/s时的水流流速分布。分别在渠道上游、闸门段、渠道下游选取4个特征断面，如图12所示。从渠道上游至下游沿x轴4个特征断面的流速分布见图13。

图12 渠道上下游流态Fig.12 The downstream channel flow regime

在闸门上游渠道1-1断面处，水流平稳，流速较低且分布均匀。在闸门环状过流面前2-2断面处，断面水深形成中部明显比两边高的趋势，流速分布不均，由于该处受浮筒闸门的阻碍作用，水流中部速度迅速减小，两侧流速增大，且由于浮筒闸体是倒置的圆锥形，故中上层的水流受到的阻碍作用较下层更大，流速较下层也更小。而该位置处的渠道下游部分，水流因冲击受到很大的扰动。在环状过流面处的3-3断面处，断面中部水深明显低于两侧，流速分布不均。由于该处水流均通过环状出流面沿y方向流入渠道下游，越接近环状出流面，水流流速越大，水面高度也越低。同时水流流入渠道下游时，由于下落高度差且水流流速较大，对下游水流造成较大冲击，而两侧水流受边壁摩擦影响较大，故流速较小。在渠道下游 4-4 断面处，水流趋于平稳，流速分布也相对均匀。

3.4 闸门前弗劳德数Fr

闸门前弗劳德数Fr也是影响闸门测流精度的重要因素之一。对于明渠测流来说，渠道上游Fr数要小于0.5才能保证上游水流的平稳，从而才能确保正确测量上游水深。数值模拟结果表明：闸门开度越大，闸门前Fr数越大；当闸门开度一定时，闸门前Fr数随着流量的增大而增大。同时结果也表明，浮筒式升降闸门的闸门前Fr均小于0.5，满足测流要求。当开度e=85 mm时不同流量工况下的闸门前弗劳德数Fr如图14所示。

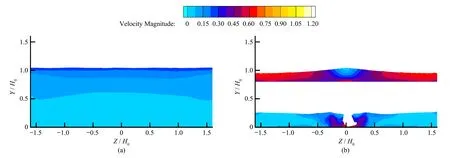
图13 各控制断面流速分布情况Fig.13 The velocity distribution of each control plane

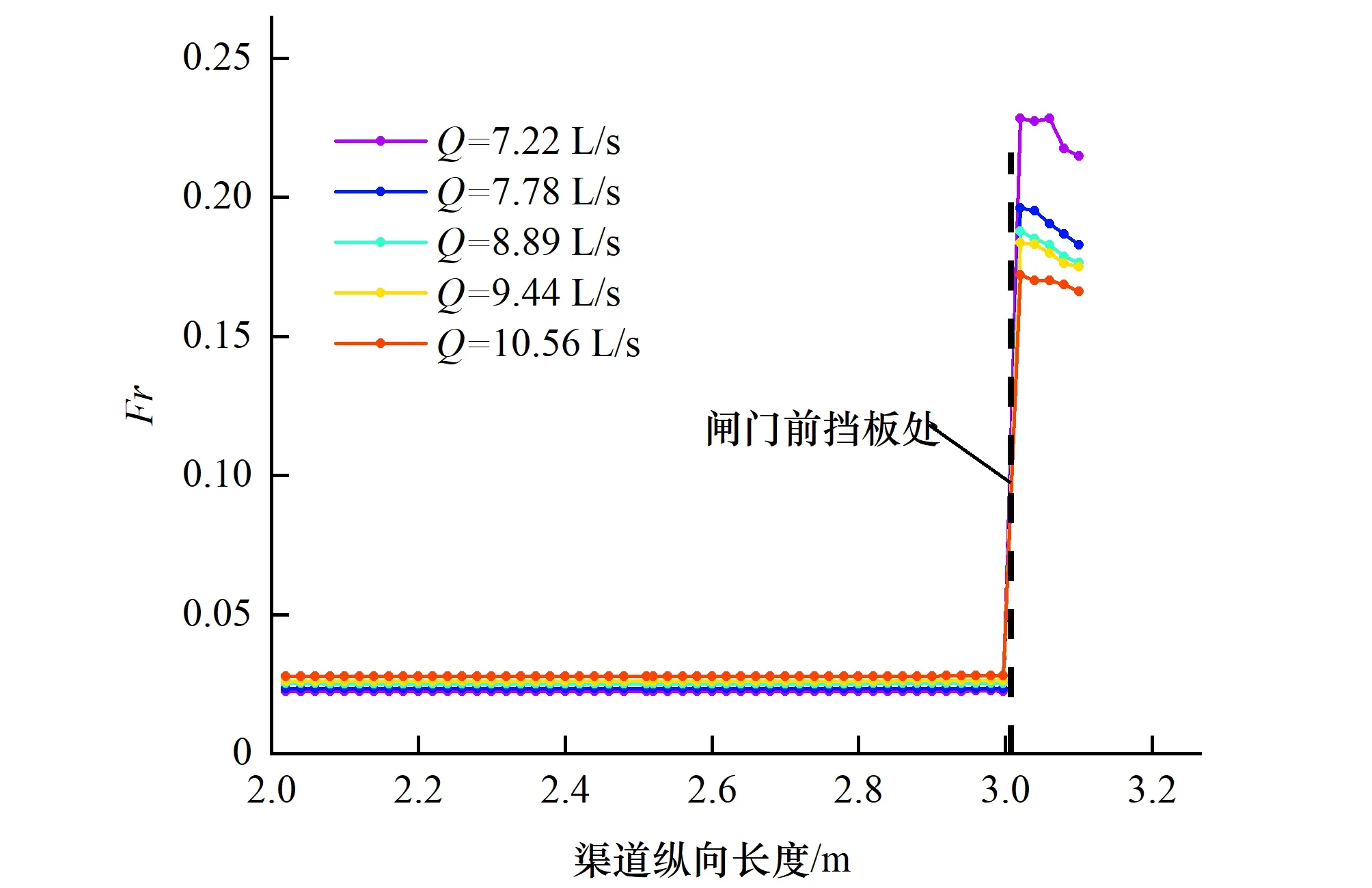
图14 闸门前弗劳德数FrFig.14 The froude number in front of the gate

3.5 测流精度

为了验证流量公式的准确性与可靠性，将测得的试验数据代入式(6)计算得到各个计算流量，再将不同开度各个流量工况下的计算流量与实测流量进行对比分析，结果如图15所示。

图15 计算流量与实测流量对比Fig.15 Contrast between measured flow and calculated flow

通过图中的对比分析结果，可得知计算流量与实测流量之间的吻合度较高，计算流量与实测流量相对误差的绝对值最大为9.4%，最小为0.04%，平均误差为0.08%，满足灌区的量水精度要求。因此，本研究所总结得出的流量计算公式能够满足灌区量水的要求，准确计算渠道的流量。

4 结 语

通过对浮筒式升降闸门的数值模拟，对其相关的水力特性与测流精度进行了深入分析，得到了以下结论。

(1)对比实测流量与模拟流量、实测水深与模拟水深，发现模拟值与实际值的吻合度较高，实测流量与模拟流量的最大误差7.96%，模拟水深与实测水深的最大相对误差为1.9%。这表明数值模拟采用的方法、边界条件、控制参数均是合理的，可以通过数值模拟的方式对浮筒式升降闸门的水力特性进行研究。

(2)通过渠道内沿程水面线的变化可以看出，在自由出流下，在闸门前一段距离内水面线较为平稳，受闸门挡板影响，水面线在前侧挡板处有微小下降，但之后又迅速恢复。而在闸门下游，受水流冲击的影响，在一定范围内水流流态复杂，水面线剧烈变化，经过一段距离的发展，水面线逐渐平稳。

(3)对流速分布进行探究，发现在闸门上游与下游水流平稳处，流速分布都较为均匀，在闸门段区域内，沿x方向由于受到浮筒与挡板的阻挡作用，流速逐渐减小，而在闸门出流面，由于出流面积小，流速逐渐增大。而且闸门前的弗劳德数Fr均小于0.5，满足测流要求。

(4)通过本文推导的浮筒式升降闸门测流经验公式，利用模拟数据进行回归分析得到了该种规格浮筒式升降闸门的流量公式，通过比对实测流量与计算流量，相对误差的绝对值最大为9.4%，最小为0.04%，平均误差为0.08%，可以看出测流公式的精度较高、形式简单、易于应用。