结合改进差分进化和模块密度的社区发现算法*
冯 勇,张冰茹,徐红艳,王嵘冰+,张永刚
1.辽宁大学 信息学院,沈阳110036
2.吉林大学 符号计算与知识工程教育部重点实验室,长春130012
1 引言
社会网络是由节点和边组成的社会结构,其中节点表示个体,边代表个体之间的各种社会关系(如好友关系、合作关系等),具体的社会网络形式诸如社交网络、科研合作网络等。社区发现即发现内聚的子集合,使集合内的节点联系比它们与集合外的节点联系更强[1]。基于检测到的社区结构可以深入揭示复杂网络的拓扑结构及功能。近年来,社区发现算法已在信息网络的语义社区发现[2]、融合多源异构数据的个性化推荐[3]等领域得到广泛应用。
社区发现算法可归结为四类:基于凝聚式与分割的算法[1,4-6]、基于标签传播的算法[7-9]、基于模块度优化的算法[5,9-12]、基于进化算法类的算法[10-12]。其中Girvan 和Newman[1]提出的经典GN(Givern-Newman)算法是一种凝聚式的算法,通过不断移除网络中最大的边介数,能够准确获得具有层级结构的社区,但该算法计算速度有待提高;Newman 在GN 算法之上提出了一种基于网络模块度最大化的层次聚类方法[5],该算法每次沿着使模块度增加最大和减小最少的方向进行合并,使社区发现的准确性得到一定程度提高;Huang等人[10]提出了一种结合差分进化的社区检测算法(cooperative co-evolutionary differential evolution based community detection,CCDECD),算法中引入协同进化框架并结合差分进化来优化网络模块度,以寻找最优的社区网络;金弟等人[11]分析了模块度函数的局部单调性,结合遗传算法,提出快速有效的局部搜索算子,可用于求解大规模社区发现问题。这些算法虽然得到了较为广泛的应用,但在发现的准确性与收敛速度方面尚存在提升空间。另外,现有算法多是基于模块度优化的算法[5,9-12],普遍存在模块度分辨率限制[13],即在计算过程中会将某些较小的社区合并,进而产生计算误差。
为克服模块度分辨率限制、提升社区发现的准确性和收敛性能,本文利用差分进化具有结构简单、易于实现、收敛快速、鲁棒性强等特点,并引入模块密度[14]作为适应度函数以解决模块度分辨率限制问题,提出了一种结合改进差分进化和模块密度的社区发现算法(improved differential evolution and modularity density community detection,IMDECD)。该方法首先对差分进化进行改进,设计了一种新的变异策略,并对F和CR变量进行动态自适应参数调整;然后将模块密度作为差分进化的适应度函数,对种群中的个体进行评价;最后基于已知的社区结构进行修改,包括基于社区变量的修正操作,以及初始化和二项交叉阶段的修改。通过对比实验,验证本文所提算法相较于凝聚式的算法(GN)、基于密度峰值的算法(overlapping community detection algorithm based on density peaks,OCDDP)、结合差分进化和模块度的算法(CCDECD and CDEMO(classification-based differential evolution algorithm for modularity optimization)),在社区发现的准确性和收敛性能方面得到一定程度的提升。
2 差分进化
近年来,基于进化算法类的社区发现算法由于其强大的全局优化能力,在很多应用场景下优于其他算法。其中差分进化[15]由于其简单性和有效性被广泛应用于数据挖掘、模式识别等领域,将其融入社区发现具有如下好处:既不需要复杂二进制编码,也不需要使用概率密度函数去自适应其个体[16],更不需要预先掌握任何关于社区结构的知识。差分进化包括三个主要步骤:变异、交叉和选择。
2.1 变异策略
目前,差分进化使用的变异策略主要有如下四种:DE/rand/1、DE/rand/2、DE/best/1 和DE/rand-tobest/1。如式(1)~式(4)所示[16]:

其中,i∈{1,2,…,NP},p1、p2 和p3 是从1,2,…,NP中随机选择的,且满足条件p1 ≠p2 ≠p3 ≠i,g是迭代次数,是目标个体是变异个体,NP为种群规模。
2.2 交叉操作
差分进化常用的交叉方式有二项交叉与指数交叉。二项交叉方案对n个分量中的每一个分量都进行交叉;指数交叉方案选择变异个体的一段,且该段以具有随机长度的随机整数k开始,该随机整数k可以包含多个分量。
由于二项交叉更易于实现,时间复杂度较低,因此本文选择二项交叉对变异个体和目标个体实施交叉操作,以产生实验个体。二项式交叉如式(5)所示:

其中,i∈{1,2,…,NP},j∈{1,2,…,n},rand是0 和1 之间的均匀分布的随机数,分别是第i目标个体、变异个体和实验个体的第j维分量。
2.3 选择操作

3 差分进化的改进
为了提高社区发现的准确性和收敛性能,本文在现有差分进化的基础上进行改进,主要改进措施包括变异策略改进以及动态自适应参数调整。
3.1 变异策略改进
在2.1 节式(1)~式(4)中,式(1)和式(2)的基矢量从种群中随机选取,具有全局搜索能力强、不易陷入局部最优的优势,但收敛速度慢;式(3)和式(4)的基矢量是当前种群中最优个体,因而局部搜索能力强,收敛速度较快但易陷入局部最优。
以上四种变异策略均存在如下问题:仅侧重准确性或收敛性中一方面的性能。例如式(1)和式(2)准确性高,但收敛速度慢,式(3)和式(4)收敛速度快,但容易陷入局部最优解,导致准确性低。因此,本文将构建一种混合变异策略以平衡准确性和收敛速度,如式(7)所示:

式(7)中采用“DE/rand/1”来保持种群的准确性,随机生成新的个体以防止种群陷入局部最优。然后采用“DE/rand-to-best/1”,利用当前种群中最优个体的信息生成新的个体,来加快收敛速度。其中fi为2.3 节中的适应度函数值,对于目标个体,如果其适应度函数值fi大于当前群体中所有个体的平均适应值fˉ,则将其归为优秀个体,采用DE/rand/1 防止陷入局部最优;否则,就将其归为淘汰个体,采用DE/rand-to-best/1 利用最优个体生成新的个体。
3.2 动态自适应参数调整
差分进化中有两个重要参数:缩放因子F值和交叉概率CR。经过实验观察和数据研究表明参数值的选择应进行自适应调整[16-17]。
式(7)中的缩放因子F值通常是常数,起到控制差异变量缩放幅度的作用。F值较小时,种群差异度减少,全局搜索能力降低,容易导致局部收敛;F值较大时,虽然容易跳出局部最优解,但收敛速度会减慢。因此,采用式(8)对F值进行动态自适应调整[17]。

其中,g是迭代次数,gmax是最大迭代次数,Fmin=0.3,Fmax=0.9。
式(5)中CR是交叉概率,CR越大收敛速度越快,但易早熟,陷入局部最优。因此,采用式(9)对CR值进行动态自适应参数调整[17],以找到使准确性和收敛性最佳的CR,其中CRmin=0.1,CRmax=0.9。

Table 1 Benchmark functions表1 基准函数

Table 2 Performance comparison of different mutation strategies表2 不同变异策略的性能比较

通过动态自适应参数调整,自适应地确定种群的变异率,从而使种群在初始阶段保持多样性,避免早熟收敛现象;并且通过逐步降低后期的突变率,避免破坏最优解,增加搜索全局最优解的可能性。
3.3 实验验证
为了验证上述对差分进化改进措施的有效性,本文在5 个常用的标准基准函数上进行测试,表1 为5 个测试函数的名称、公式、搜索空间和最优值,其中F1、F2 是单峰函数,F3~F5 是多峰函数。
将本文3.1节和3.2 节中的改进策略相结合,命名为IMDE(improved differential evolution),与式(1)~式(4)的变异策略进行比较,同时选择与本文改进策略相近的文献[17]中的变异策略DE_version 1 进行比较,其中每个变异策略的F值和交叉操作中的CR值均由式(8)和式(9)计算所得。实验结果如表2所示,结果包括30 次独立运行测试的平均值和标准差(表2中括号内的数据为标准差)。在实验中,选择与变异策略DE_version 1 相同的实验参数:种群规模大小NP=100,维度大小D=30,F∈[0.3,0.9]和CR∈[0.1,0.9]。
表2 从准确性和收敛性能两方面对6 种变异策略进行了比较,平均值体现准确性,标准差体现收敛性能,每种情况下的最优解都用粗体表示,可以看到,本文提出的改进策略IMDE 明显优于其他5 种变异策略,在80%的测试函数上获得了最优解。
通过表2 可以看出,IMDE 与式(1)DE/rand/1 单独比较,在F1~F4 这4 个函数上标准差均有显著提高,验证了IMDE 采用“DE/rand-to-best/1” 可加快收敛速度;再与式(4)DE/rand-to-best/1 单独比较,在F1~F4 这4 个函数上解的准确性有了显著的提高,验证了IMDE 采用“DE/rand/1”可防止种群陷入局部极值,提高了差分进化算法求解全局极值的能力。
以上结果表明,本文对差分进化的改进措施是有效的,能够提高原差分进化的准确性和收敛性,并且有效提高了种群质量和全局收敛能力,为社区发现的模块密度优化问题提供了一种有效的优化方法。
4 结合改进差分进化和模块密度的社区发现
本文利用上述改进差分进化的优势,结合模块密度,对社区发现算法的改进策略开展研究。首先,在初始化阶段,将网络中每个节点用社区标识符进行规范化表示;然后,进行适应度函数设置,针对模块度存在的分辨率限制问题,用模块密度[14]代替模块度作为适应度函数;最后,利用已知的社区结构,进行修改操作,包括基于社区变量的修正操作,以及初始化和二项交叉阶段的修改。
4.1 初始化
对于具有n个节点的复杂网络G=(V,E),种群中的第k个个体由式(10)构成:

其中,ci表示节点i所属社区,即社区标识符。IMDECD 在初始化时,每个节点所属社区是随机分配的,因此G中最多存在n个社区,社区标识符的最大值为n。
例如,图1(a)显示了一个包含7 个节点的网络。根据社区结构的定义,将网络划分为两个以不同颜色节点表示的社区。图1(b)是基于社区标识符的向量表示。

Fig.1 Vectorization representation of individuals图1 个体的向量化表示
4.2 适应度函数设置
适应度函数通常有模块度和模块密度两种,模块度Q函数作为社区发现算法研究历史上的里程碑,由于其易于实现而被广泛应用在社区检测中,基于模块度优化的算法已经成为社区发现算法中的一个研究领域。
但是,Q有几个缺点:首先,最大化Q值被证明是NP 问题。其次,Q值大并不总是有意义的,存在没有社区结构的随机网络也可以拥有很大的Q值的情况。最后,Q具有分辨率限制,最大化Q不能发现社区规模较小的社区,Q值的表示如式(11)所示[10]:

为了克服模块度的分辨率限制,提高算法的准确性,Li 等人[14]在经过一系列理论推导和实践测试后,提出了一种模块密度计算方法,如式(12)所示。经Sato 等人[13]的实验验证,证实了模块密度解决分辨率限制问题的有效性。因此,本文选择模块密度作为适应度函数。

其中,m为划分完成后的社区数量,λ为0 到1 之间的数,L(Vi,Vi) 为子网络Gi内的节点之间度数之和,为Gi内的节点与Gi外其他节点的度数之和,为Gi的节点数量。
4.3 基于社区结构的修改
由于差分进化在进行函数求解和社区发现上存在差异,本文在结合改进差分进化和模块密度时,利用已知的社区结构,进行以下修改操作,以提高计算的准确性。
(1)社区变量CV(i)
在社区发现的迭代过程中,可能会出现某些节点被放入错误的社区的情况,这些错误会削弱算法寻找最优解的能力,降低准确性。
为解决上述问题,本文采用Tasgin 和Bingol[18]提出的基于社区变量CV(i)的修正操作,以减少节点被分配错误的情况。CV(i)被定义为节点i及其邻居节点不在同一社区中的个数与节点i的度的比值,如式(13)所示:其中,deg(i)是第i个节点的度,ci是包含第i个节点的社区。

修正操作过程如下:首先,随机选择一些节点。然后,对每个节点计算其社区变量,并与阈值进行比较,阈值是在反复实验之后获得的预定义常数,本实验中取0.3。如果该节点的社区变量大于这个阈值,则该节点及其所有邻居将被放入同一社区,新社区为邻居节点中包含最多节点数量的社区。否则,该节点将不执行任何操作。
通过基于社区变量的修正操作,每次节点被分配时,都会考虑到其邻居节点,可减少节点分配错误的情况,提高准确性。
(2)初始化阶段
在初始化过程中,每个节点是随机分配到一个社区中的,然而这可能会导致一些没有联系的节点被分配到同一社区。为减少计算量,对初始化阶段进行修改[18]。
修改后的初始化过程如下:一旦生成一个个体,就随机选择个体中的节点,将其社区标识符分配给其邻居节点,生成初始种群,让每个节点与其邻居节点在初始化阶段处于同一个社区中。通过此操作,限制了可能解的空间,消除了不必要的迭代,提高了IMDECD 算法的收敛速度。
(3)二项交叉阶段
由于每次分配社区标识符都是随机的,可能会出现以下情况:对于两个个体{1,1,1,2,3} 和{3,3,3,2,1},节点i多次分配到相同的社区,但每次对应的社区标识符却不同,即社区和社区标识符之间不是一对一的对应关系。若按社区标识符统计节点i被分配到哪个社区时,就会出现错误结果,进而导致节点i被划分到错误的社区中。这种情况下,若想得到正确的统计结果,算法必然要根据邻居节点、社群结构判断不同的标识符是否对应同一社区,因而会导致搜索最优解的效率下降。基于以上考虑,根据文献[18]对交叉操作进行如下修改。
提高语文课堂教学效率,是当今语文教学的迫切要求,是语文教师不可推卸的责任。教师只有从培养学生良好的课堂学习习惯、激发学生学习语文的兴趣、引导学生将学与练结合、指导学生学习的方法等方面着手,才能真正提高语文课堂教学的效率,减轻学生的课业负担,让学生乐于学习。
二项交叉过程的修改:首先,为每个i∈{1,2,…,NP}设置实验个体ui=xi。然后,对每个j∈{1,2,…,n}考虑ui和变异个体vi中的第j个分量。如果rand≤CR,找到社区标识符为vi,j的所有节点,然后将ui中相应节点的社区标识符分配为vi,j,实现对应关系;否则,将不对ui执行操作。
修改后的二项交叉使每个社区有唯一的标识符与之对应,因而不会出现节点被分到同一社区却对应不同标识符的情况,因此仅通过社区标识符就可以完成统计功能,从而提高算法搜索最优解的效率。
4.4 算法描述
结合社区结构,IMDECD 算法的具体执行步骤如下:
(1)初始化IMDECD 算 法的相关参数NP、n、gmax,详见第5 章实验参数设置。
(2)根据修改后的初始化过程,生成NP个n维向量组成初始群体P0={x1,x2,…,xNP},其中每个个体xk由式(10)表示。计算P0中每个个体的模块密度值,并保存当前最优个体及其对应的模块密度值。
(3)If(g<gmax)Then
①由式(7)和式(8)组成的自适应混合变异策略,对种群中的每个个体执行变异操作,生成对应的变异个体;执行式(13)中的修正操作,校正中的偏移向量。
②由式(5)和式(9)组成的自适应交叉策略,对种群中的每个个体执行修改后的二项交叉操作,生成对应的实验个体;执行式(13)中的修正操作,校正中的偏移向量。
③采用式(6)的贪婪选择策略,分别将种群中的目标个体与其对应的实验个体进行比较,选择其中的较优个体组成下一代种群Pg+1。式(6)中的适应度函数使用式(12)中给出的模块密度。
④g=g+1。
(4)算法运行结束,输出对复杂网络社区结构的最优划分结果以及对应的模块密度值。
4.5 时间复杂度分析
假设社区网络中节点数为n,边数为t,划分完后的社区数量为m,种群规模为NP,迭代次数为g。对于具有n个节点的社区网络,本文的模块密度函数时间复杂度为O(g2×NP×m),式(7)的混合变异策略和式(6)的贪婪选择策略的时间复杂度均为O(g2×NP),式(5)的自适应交叉策略的时间复杂度为O(g2×NP×n),因此本文算法的时间复杂度为O(g2×NP×(n+m)),与其他算法的时间复杂度的对比如表3所示。
由表3 可知,IMDECD 算法在时间复杂度上明显优于GN 算法和OCDDP 算法。与CDEMO 算法相比,当节点数n大于迭代次数g时,IMDECD 算法的时间复杂度低,即更适合规模较大的复杂网络。与CCDECD算法相比虽然时间复杂度持平,但后续实验证明本文算法具有更高的准确性和更好的收敛性能。

Table 3 Comparisons of time complexity表3 时间复杂度比较
5 实验与结果分析
本文实验硬件环境为Intel®Pentium®,CPU 3.0 GHz,内存8.0 GB,仿真软件为Windows 10 系统和Matlab R2017a。本文选择计算机生成网络和5个不同规模的真实世界网络开展实验,将所提算法与GN[1]、OCDDP[19]、CCDECD[10]以及CDEMO[17]算法进行比较。为了减少统计误差,在每个数据集上独立运行算法30 次,选择平均值进行比较,所有算法的实验参数设置和环境配置均相同。
根据数据集规模大小进行参数设置,在Karate 网络中设置种群规模大小NP为20,最大迭代次数为50;Football 网络中NP设置为30,最大迭代次数为300;在Jazz 和US AirLines 网络中NP设置为30,最大迭代次数为600;在Polblogs 网络中NP设置为60,最大迭代次数为600。
本文选择式(11)所示的模块度Q值和式(14)所示[17]的互信息值NMI作为评价函数:

5.1 计算机生成网络
本文采用Lancichinetti 提出的人工计算机生成网络GN Benchmark[20]验证IMDECD 算法检测网络社区结构的性能。GN Benchmark 网络中有128 个节点,它们被分成4 个社区,每个社区有32 个节点。
上述网络中的混合参数μ主要用于确定某一社区中任意一个节点与其他社区的节点之间共享边的数量,随着μ的不断增大,网络中的社区结构将变得越来越模糊,性能一般的社区发现算法的NMI会开始下降,以此达到区分的目的。
图2给出了IMDECD 算法与其他对比算法在GN Benchmark 网络上,随μ值的增大NMI的变化情况。

Fig.2 Average NMI of IMDECD and other algorithms图2 IMDECD 与其他算法的平均NMI
从图2 可以看出,与其他4 种算法对比,随着μ的不断增大,IMDECD 算法的性能优势变得越来越明显。当混合参数μ等于0.7 时,才开始出现下降,结果验证了IMDECD 算法的有效性。
5.2 真实世界网络
本节采用5 个具有代表性的、不同规模大小的真实网络数据集进行测试,各数据集的详细信息如表4所示,包括空手道俱乐部网络[21](Karate)、美国大学生2000赛季美式足球联赛网络[1](Football)、爵士音乐家合作网络[22](Jazz)、美国航空网络[23](US AirLines)以及2004 年美国大选政治博客网络[24](Polblogs)。表4 说明了数据集的规模:节点数和边数。

Table 4 Real network dataset表4 真实网络数据集
关于模块密度Dλ中的λ取值为λ∈(0,1)。为分析λ对本文算法社区发现结果产生的影响,取λ不同数值下对社区发现结果的模块度Q值和互信息值NMI的影响情况。图3 为Karate 网络的社区发现结果随λ值变化的结果。

Fig.3 Effect of λ on Q and NMI in Karate network图3 Karate网络中λ 对Q 值和NMI 的影响结果
从图3 中可以看出,在Karate 网络中,当λ=0.3时,NMI=1,Q=0.371 8,其社区划分后的结果与真实的网络社区一样,Q值却较低;当λ=0.6,0.7,0.8 时,Q值均为0.419 8,NMI值却分别为0.725 3、0.639 9、0.652 8。因此,在Karate 网络中,当λ=0.6 时,NMI=0.725 3,Q=0.419 8,两者的值都较高。
图4 显示Football 网络的社区发现结果随λ值变化的结果。

Fig.4 Effect of λ on Q and NMI in Football network图4 Football网络中λ 对Q 值和NMI 的影响结果
从图4 中可以看出,在Football 网络中,λ=0.4~0.8 时,Q值变化不大,均在0.604 6 左右,NMI值变化较大。当λ=0.6 时,NMI值最大,为0.935 4。因此,在Football网络中,当λ=0.6 时,NMI=0.935 4,Q=0.604 6,两者的值都较高。
由于Karate 和Football 网络都有已知的社区结构,可以用模块度Q值和互信息值NMI两个标准来衡量社区划分的结果;而Jazz、US AirLines 和Polblogs 网络没有已知社区结构,因此只能以模块度Q值为标准来衡量。图5为其他3个网络的社区发现结果随λ值变化的结果。可以看出,当λ=0.6 时,Q值都较高,因此模块密度Dλ中的λ取值0.6。
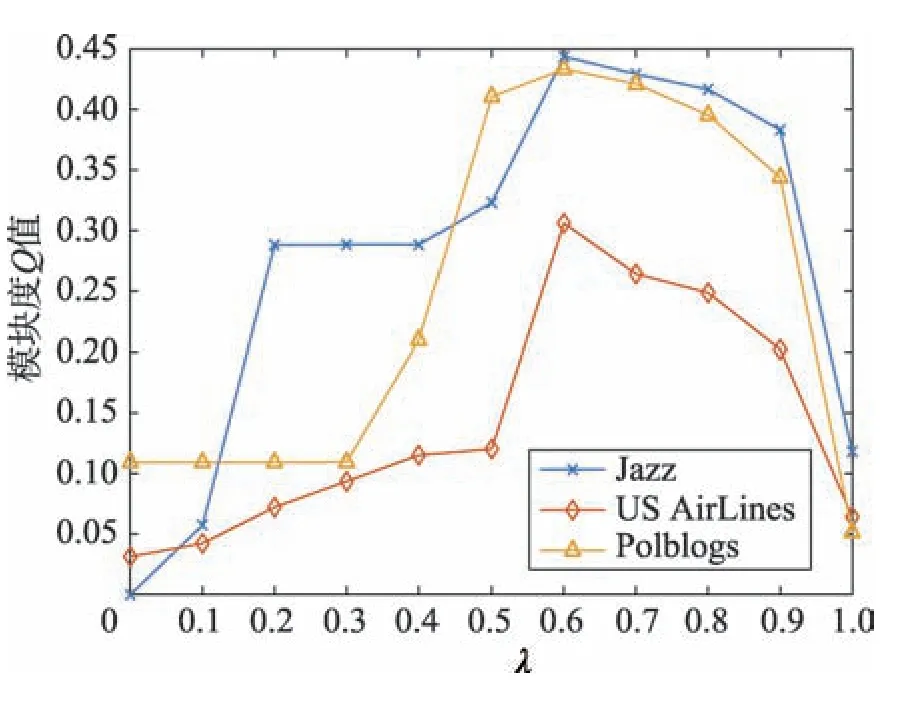
Fig.5 Effect of λ on Q in other networks图5 其他网络中λ 对Q 值的影响结果
5.3 结果分析
根据以上研究,表5和表6为每个算法在5个数据集上独立运行30次后的实验结果,表中包括:模块度Q的平均值、互信息值NMI、标准差和社区个数。表中数据格式说明:0.419 8/4,其中0.419 8 表示模块度,4 表示社区个数;(0.00E-00)表示运行30 次的标准差。
从表5和表6中可以看出,相对于其他算法而言,IMDECD 在5 个真实网络数据集上具有较好的效果。
表5 中,在Karate 网络,IMDECD 的Q值和标准差与CCDECD、CDEMO 同时达到最优,Q值相较于OCDDP 提高了3.3%,与GN 相比提高了4.6%;互信息值NMI未达到最优,这是因为GN 算法更适合小规模网络;在Football 网络中NMI达到最优,Q值和标准差较低,这说明IMDECD 在Football 网络上的划分结果和真实网络划分最为接近,但由于真实网络的模块度并不高,导致IMDECD 算法的Q值较低,也说明了IMDECD 算法不适合规模较小的网络。
表6 中,IMDECD 在Jazz、US AirLines 和Polblogs这3 个网络的Q值和标准差都最优,这说明本文所提IMDECD 算法更适用于规模较大的网络。因此,相较于其他4 种算法,本文提出的算法在社区发现方面具有更高的准确性和更好的收敛性能。

Table 5 Comparison of NMI and modularity between Karate and Football network表5 Karate和Football的NMI、模块度比较

Table 6 Comparison of modularity of other networks表6 其他网络的模块度比较
关于分辨率限制,4 个对比算法中,CCDECD 和CDEMO 算法是基于模块度优化的算法。在Football、Jazz、US AirLines 以及Polblogs 网络中,IMDECD 算法划分的社区个数均大于CCDECD 和CDEMO 算法,表明使用模块密度的IMDECD 算法能划分得到更多的社区,即能分辨出更多较小的社区。
6 结束语
为克服模块度分辨率限制,提升社区发现的准确性和收敛性能,本文提出了一种结合改进差分进化和模块密度的社区发现算法。该算法首先调整差分进化的变异策略,并对F和CR变量进行动态自适应参数调整;然后针对模块度的分辨率限制问题,将模块密度作为差分进化的适应度函数,对种群中的个体进行评价;最后基于已知的社区结构进行修改,包括基于社区变量的修正操作,以及初始化和二项交叉阶段的修正。对比实验表明,本文提出的IMDECD 算法具有更高的社区发现准确性和更好的收敛性能,更强的寻优能力与鲁棒性,能够有效探测真实世界网络中存在的社区结构。

