构造性覆盖算法的SMOTE 过采样方法*
严远亭,朱原玮,吴增宝,张以文,张燕平
安徽大学 计算机科学与技术学院,合肥230601
1 引言
在生物医学数据分析[1-3]、卫星雷达图像中溢油的检测[4]、文本分类[5]和欺诈电话的检测[6]等很多实际的应用领域中,处理的对象往往是不平衡数据集。不平衡数据集[7]是指数据集中某类样本的数量明显少于其他类样本的数量。为了描述方便,一般将数量较多的样本称为负类样本,数量较少的样本称为正类样本。在处理不平衡数据集分类问题上,传统的机器学习分类算法总会倾向于负类样本的预测,从而导致正类样本的识别能力下降。在很多情况下,识别出正类样本要比识别出负类样本更为重要,甚至会涉及到分类代价敏感问题[8]。因此,如何有效地提高不平衡数据集中少数类样本的分类准确率和整体准确率成为机器学习领域的一个研究热点和难点。
在解决不平衡数据分类问题上,近十年来众多国内外学者做了大量的研究工作,主要概括为以下两类:一个是从数据集层面;另一个是从算法层面。其中,从数据集层面[9]是通过一些机制改善不平衡数据,获到均衡的数据分布,常见的策略包括过采样技术和欠采样技术,一种常用的过采样方法是Chawla等[10]提出的合成少数类过采样技术(synthetic minority over-sampling technique,SMOTE)。SMOTE 方法的优点在于它能使决策区域更大,但也存在两方面的缺陷:一是在选择最近邻时存在一定的盲目性,即如何确定K值才能使算法达到最优是未知的;二是该算法无法克服不平衡数据集的数据分布问题,即容易产生分布的边缘化问题。在少数类中,不同样本在过采样过程中的作用并不相同,处于少数类边界的样本往往比处于少数类中心的样本作用更大。
为了解决上述SMOTE 方法盲目性和边缘化的问题,Han等[11]提出基于SMOTE的Borderline-SMOTE算法,算法通过比较少数类样本近邻中多数类与少数类样本的个数,来判断该样本是否处于少数类样本的边界,然后只对少数类的边界样本进行SMOTE过采样处理。He等[12]提出一种自适应合成采样(adaptive synthetic sampling,ADASYN)算法,算法以样本的分布为标准,动态地确定合成样本的总数量,并自适应地改变不同少数类样本的权重,为每个样本合成相应数量的样本。Calleja 等[13]提出D-SMOTE 算法,利用求最近邻样本均值点生成人工合成样本。陈思等[14]提出在数据处理之前对数据进行聚类融合,判定在多次聚类过程中总是处于同一类簇的样本为中心样本,总是变化所属类簇的样本为边界样本,然后对少数类的边界样本进行SMOTE 采样,对于多数类的中心样本进行欠采样。Barua 等[15]提出(majority weighted minority over-sampling technique,MWMOTE)算法,该方法首先识别难以学习的信息类样本,并根据其与最近的多数类样本之间的欧氏距离赋予它们权重,然后利用聚类方法从加权信息类样本中生成合成样本,这样所有生成的样本都位于某个少数类的集群中。陶新民等[16]提出基于代价敏感的支持向量机算法,首先利用边界人工少数类过采样技术(Borderline-SMOTE)实现训练样本的均衡,然后利用K近邻构造代价值,同时利用每个样本的代价函数来消除噪声样本对SVM(support vector machine)算法精度的影响。Batista 等[17]提出了SMOTE+Tomek-Link 的方法,首先对原始的数据集进行SMOTE 过采样,然后将Tomek 链作为清除数据的方法,生成具有定义明确的类集群的平衡数据集。
上述方法从不同的侧重点对不平衡数据进行了处理,但这些方法在筛选少数类关键样本方面仍存在一定的不足。为了解决此问题,本文提出一种基于构造性覆盖算法[18]的不平衡数据分类算法(constructive covering algorithm-based minority oversampling technique,CMOTE)。该算法提供了两种不同的策略(覆盖内样本个数和覆盖密度)对少数类中关键样本进行选择。首先,利用构造性覆盖算法找出少数类样本的所有覆盖;然后,选择覆盖中样本数或样本密度不大于给定阈值的样本作为过采样过程的输入;最后,对所选样本使用SMOTE 生成新的少数类样本,并将其与原始数据集结合作为训练集构造分类器。
2 SMOTE 算法
SMOTE 是一种基于随机过采样算法的改进过采样方法[19],应用十分广泛。SMOTE 的基本思想是利用K近邻[20-21]和线性插值[22],在相距较近的两个少数类样本间按照一定的规则人工地插入新的样本,以达到使少数类样本数目增加,数据集趋于平衡的目的。算法具体过程描述如下:
(1)对于少数类中每一个样本x,以欧氏距离为标准计算它到其他每一个少数类样本的距离,得到其K近邻。
(2)根据样本不平衡程度设置一个采样倍率N,对每一个少数类样本x,从其K近邻中随机选择若干个样本,假设其中一个选中的近邻为xn。
(3)对于每一个随机选择的近邻xn,按照式(1)构建新的样本Xnew:

(4)把人工合成的新样本与原始数据集组成一个新的数据集,然后利用分类器对其进行分类。
为了更直观地表述,图1(a)表示少数类样本x利用K近邻找出最近的同类样本点,图1(b)中Xnew表示利用最近邻和线性插值的方法生成少数类样本点。

Fig.1 SMOTE schematic chart图1 SMOTE 示意图
3 构造性覆盖算法的少数类过采样技术
3.1 构造性覆盖算法
构造性覆盖算法(constructive covering algorithm,CCA)可以看作一个三层的神经网络分类器,包括输入层、隐藏层和输出层。
输入层共有n个神经元,每个神经元对应样本的一维特征属性,假定X={(xi,li)|i=1,2,…,t,li=1,2,…,m}为给定的数据集,t和m分别表示样本数目和类别数目,即。
隐藏层共有s个神经元,初始时为0 个,每一个球形覆盖对应一个神经元,每个神经元的权值为覆盖的中心点,阈值为覆盖的半径。对所有的样本进行覆盖,求得的一组覆盖表示为表示第i类样本的第j个覆盖。隐藏层共有s=∑ni个覆盖,其中ni代表第i类的覆盖个数,i=1,2,…,m。
输出层共有m个神经元,第i个神经元的输入为类别相同的一组覆盖,输出为该类别。例如当输出Ot=(o1=0,o2=0,…,oi=1,…,om=0),oi=1 表示第i个样本的输出。
CCA 根据样本之间的距离构造一个覆盖,首先找到不同类别的最近样本,然后找到相同类别的最远样本。值得注意的是,求最大距离等于求最小内积,在构造覆盖时用内积来描述CCA。CCA 算法描述如下[23-24]:
(1)根据式(2)将全部样本投影到n+1 维的球面空间。

(2)随机选择一个样本xi作为覆盖中心点,根据内积计算公式分别计算最大内积d1(k)和最小内积d2(k)。

(3)计算覆盖半径:

(4)根据xi和θ构造一个覆盖,即一个隐藏神经元。
(5)从训练集中删除覆盖内的样本,回到步骤(2),直到所有的样本都被覆盖。
从以上描述很容易看出,如果学习了一个样本,它将立即从训练集中移除,CCA 算法避免了迭代计算。此外,CCA 算法从一个空的隐藏层开始,并根据后续数据的位置扩展现有的隐藏神经元,该学习过程避免了盲目选择神经网络的结构。覆盖的形成十分适合在不平衡数据中为SMOTE 算法寻找候选样本。
3.2 CMOTE 算法
在少数类中识别哪些关键样本进行过采样,与数据集的不平衡度、样本整体分布情况、少数类内部样本分布情况、样本个数、样本属性个数以及样本属性的类型都有一定的关系。这是一个复杂的优化问题,确定数学模型比较困难。从构造性覆盖算法的构建过程来看,其能够从一定程度上挖掘样本空间领域的信息,因此本文基于CCA 这样的特点,提出利用CCA 来进行关键样本的选择。
根据上述提到的CCA 与SMOTE 算法,本文提出基于以上两种算法的不平衡数据分类算法(CMOTE算法),识别不平衡数据集中容易被误分的少数类样本。
首先,该算法利用构造性覆盖算法对不平衡数据求覆盖,每一个覆盖包括覆盖类别、覆盖内样本数、覆盖半径和覆盖中心点样本。对于少数类样本形成的覆盖,如果覆盖包含较多个样本,则该覆盖中的样本易于分类,对于提高识别少数类样本模型的能力贡献不大。
其次,本文提出了两种策略来确定选择哪些少数类样本来生成新样本。(1)若覆盖内的样本数量小于特定阈值P,则覆盖内的样本视为关键样本;(2)若覆盖内的样本密度小于特定阈值D,则覆盖内的样本视为关键样本。
按照CCA的构建过程,本文定义如下的覆盖密度:

其中,m表示的是第i个少数类样本的覆盖中样本的个数,r是覆盖的半径,其值由式(3)~式(5)求得。
算法1基于构造性覆盖算法的少数类过采样技术
输入:训练集T={(x1,l1),(x2,l2),…,(xn,ln)},阈值P,阈值D,采样倍率N。
输出:合成的少数类样本集合。

最后,使用SMOTE 算法对上述关键样本合成新的少数类样本。CMOTE 算法的具体过程描述如算法1 所示。
为了直观地描述CMOTE 算法,以二维数据为例,算法的大致过程如图2 所示。图2(a)中少数类样本B是利用构造性覆盖算法筛选出容易被误分的样本点。图2(b)中的少数类样本B利用SMOTE 算法按照特定的比率N合成新的样本,新样本与原数据集组合成新的数据集,新数据集使用WEKA 平台[25]中的C4.5 决策树分类算法进行分类。
4 实验与分析
4.1 评价标准

Fig.2 CMOTE schematic chart图2 CMOTE 示意图
在不平衡数据分类中,少数类样本更容易被错误分类,少数类样本的错误分类对分类器整体分类性能[26]的影响很小。例如,当少数类样本数目所占不到1%时,即使所有的少数类样本被错误划分成多数类样本,整体的分类准确率也可以达到99%,但少数类的分类准确率为0。在实际应用中,识别少数类样本的正确率尤其重要[27]。研究表明,当存在类的不平衡问题时,最常用的性能度量“精度”已经不能准确地度量分类器的性能,因为它不能分别反映出正类和负类的真实分类性能。
一些研究者在研究不平衡数据集分类指标时没有使用整体的分类性能,ROC 曲线下面积(AUC,缩写为RA)和准确率、召回率、F-measure、G-mean 等指标更适合评价对少数类的分类性能。因此,本文以准确率、召回率、F-measure、G-mean 和AUC为主要评价指标。召回率用于评价不平衡数据集中少数样本的正确率。F-measure 用来评价不平衡数据集中少类样本的分类性能,G-mean 用来评价整体分类性能[4]。
机器学习算法的性能通常由一个混淆矩阵来评估,如表1 所示(针对一个2 类问题)。通常把少数类样本的标签视为正,多数类样本的标签视为负。表的第一列为真正的类标签,第一行为预测的类标签。TP和TN分别表示正确分类的正类和负类样本个数,FN和FP分别表示错误分类的正类和负类样本个数。

Table 1 Confusion matrix of binary classification tasks表1 二分类任务的混淆矩阵
由上述的混淆矩阵可以得到以下公式。
少数类样本的召回率为:

少数类样本的准确率为:

在上述指标的基础上,定义F-measure(简称F1):

其中,β表示Recall与Precision的相关重要性,本文中取值为1,从定义可以看出,Recall和Precision可用来评估少数类的分类性能,只有Recall和Precision都比较大时,才能获得较大的F-measure 值,因此Fmeasure常用来评估分类器对于少数类的分类准确率。
Kubat等[28]提出G-mean 作为评价指标:

其中,TPrate用来评估少数类的分类性能,TNrate用来评估多数类的分类性能。从定义可以看出,只有TPrate和TNrate都比较大时,才能获得较大的G-mean 值,因此G-mean 常用来评估数据集整体的分类准确率。
4.2 实验数据集
本文使用文献[29]中的前11 个不平衡数据集,这些数据集在http://www.keel.es/dataset.php 上公开可用,连同从UCI 数据库下载的数据集Satimage 来验证本文方法的性能。特别地,对于数据集Satimage,类4的样本被认为是少数类,其余类的样本被认为是多数类。对于每个数据集,数据集的详细信息包括名称(Dataset)及其缩写(Abb)、样本数量(#Ex.)、属性个数(#Atts.)、少数类和多数类样本所占总样本的百分比{mr,MR}以及数据集的不平衡率(imbalanced ratio,IR),都在表2 中列出。

Table 2 Basic information of datasets表2 数据集基本信息
4.3 算法参数的确定
为了筛选出容易被错误分类的样本,需要确定CMOTE 中的两个参数,即P值和D值。确定P值是因为覆盖内的样本中,样本数量较少的样本很有可能是噪声样本或重叠样本;D值则是用来衡量样本的聚集程度,对于D值较小的覆盖,这些样本更有可能是噪声或重叠样本。
表3 和表4 中显示了不同参数P和D对应的性能指标,最好的实验结果以粗体显示。表3 表明了参数P与CMOTE1 性能之间的关系。从实验结果可以看出,当P=1 时,5 种评价指标,Precision、F-measure、G-mean、Recall和AUC(缩写为P1、F1、G1、R1 和AU)在更多的数据集上可以获得最优值,分别为:P1,8 个数据集;F1,11 个数据集;G1,8 个数据集;R1,10 个数据集;AU,7 个数据集。表4 给出了参数D与CMOTE2 性能之间的关系,当D≤0.1 时,5 种指标可以在大多数数据集上得到最优值,数据集数目分别为9、11、8、9、10。D≤0.1 的情况下,Recall在Y04 数据集上没有得到最大值,但与最优性能之间只有0.4%的差距,可以忽略。因此,本文将P的值设为1,D的值设为0.1。
确定上述两个参数后,可筛选出少数类中更容易被误分的样本,对这些关键样本用SMOTE 方法进行过采样。表5 给出了每个数据集在SMOTE 算法中特定的采样比率N,其中第2 列和第4 列表示两个不同阈值P和D下对应的采样比率,即以每个关键样本为种子需要扩充的少数类样本个数。
4.4 实验结果与分析
本实验采用C4.5 决策树[30]作为分类算法,该部分主要展示了本文提出的CMOTE算法与对比算法的实验结果,并对算法的分类性能进行了分析。对于每一个算法,进行10次10折交叉验证,取平均值作为平均性能。为了简便起见,本节中列出了3 个重要指标F-measure、G-mean 以及AUC的对比结果。表6、表7给出了7 种算法在F-measure、G-mean 评价指标上的结果,最后一行给出了每种算法在12 个数据集上的平均值,最佳结果以粗体显示。为了方便,将算法SMOTE、Borderline-SMOTE、SMOTE+TomekLin、ADASYN、MWMOTE、CMOTE1 和CMOTE2 分 别缩写为SMO、B-SM、SM-T、ADAS、MWM、CSM1 和CSM2。

Table 3 Results of metrics corresponding to different P values表3 不同P 值对应的性能指标结果
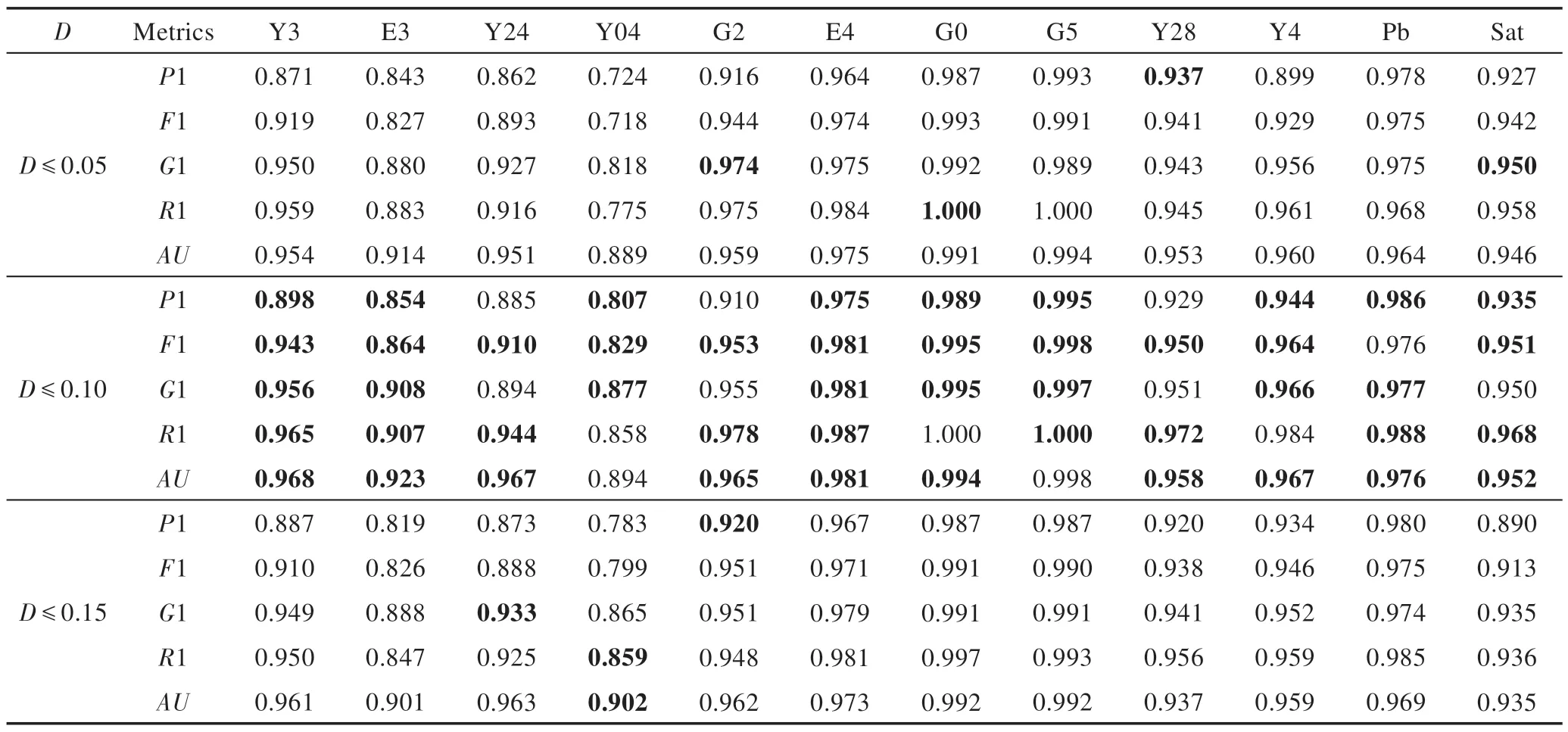
Table 4 Results of metrics corresponding to different D values表4 不同D 值对应的性能指标结果

Table 5 Sampling rate corresponding to different P and D表5 两个不同阈值P/D 对应的采样率

Table 6 Experimental results on F-measure表6 指标F-measure上的实验结果

Table 7 Experimental results on G-mean表7 指标G-mean 上的实验结果
从表6、表7 可以看出,本文所提到的过采样技术在F-measure、G-mean 指标上对大部分数据集都得到了有效的提高。例如,在F-measure 上,本文方法在12 个数据集中的9 个有最高的F-measure 值。与ADAS 算法相比,CSM1 和CSM2 在某些数据集上甚至有超过10 个百分点的提升。而对于G-mean,本文方法在12 个数据集中的7 个数据集上取得了最优值,与ADAS 算法相比,CSM1 和CSM2 的G-mean 分别提高了4.29 个百分点和4.50 个百分点。
AUC被认为能够更好地衡量对少数类样本的分类性能。图3 给出了7 种算法在AUC上的结果,最后一组为AUC在12 个数据集上的平均值。从图3 中可以看出与ADAS 算法相比,CSM1 和CSM2 的AUC上分别有明显的提高。相对于性能较好的SM-T 算法,本文算法在大部分数据集(12 个数据集中的10 个)上的AUC都取得更优值。另外从平均的角度来看,本文提出的两种过采样技术的策略在F-measure 和Gmean 这两种指标上都得到了明显的改进。

Fig.3 Experiment result on AUC图3 指标AUC 上的实验结果
本文还对算法的性能进行了统计比较。图4 和图5 给出了CSM1 和CSM2 与其余5 种算法在每个指标上Welch t 检验的p值的实验结果图,细节如图4和图5 中子图所示。总体上,对比算法的Recall、Fmeasure、G-mean 和AUC与CSM1 和CSM2 都有显著差异。至于Precision,算法性能仅在几种对比算法上与CSM1 和CSM2 有显著差异(5 种算法中有2 种)。从实验结果来看,CSM2 方法略优于CSM1 方法,CSM1有14个较好的结果,CSM2有18个较好的结果。说明了本文所提出的CMOTE 算法可以在大多数数据集上表现出最佳性能。
5 结论

Fig.4 Experiment result of Welch p between CSM1 and 5 algorithms图4 CSM1 和5 种算法的Welch p 实验结果

Fig.5 Experiment result of Welch p between CSM2 and 5 algorithms图5 CSM2 和5 种算法的Welch p 实验结果
作为一种典型的过采样技术,SMOTE 及基于SMOTE 改进的方法受到了越来越多的关注。本文针对SMOTE 方法所存在的缺陷,引入了构造性覆盖算法CCA 来选择用于SMOTE 过采样的关键少数类样本。CCA 作为一种监督学习模型,能够有效地检测出对分类边界影响较大的关键样本。在12 个数据集上的实验结果表明,在给定合适的参数下,CMOTE 算法的性能在不平衡数据分类方面于其他对比算法有了很大的提高。

