电子战飞机海上作战航路计算方法研究∗

顾小港 李仙茂 甘厚吉 高金龙

（1.海军工程大学学员二大队5队 武汉 430033）（2.海军工程大学电子工程学院 武汉 430033）

1 引言

未来战争是高度信息化的战争，“非对称、非接触、非线性”是未来战争的主要特点，空袭尤其是远距离奔袭已成为主要战术手段，在海上作战中更占据着不可替代的位置［1］。在现代战争中，电子战飞机正发挥着越来越重要的作用。电子战飞机的干扰方式有伴随干扰和远距离支援干扰两种，但以伴随干扰为主要作战方式。伴随干扰一般用于电子战飞机在伴随突击兵力进入对方火力打击圈的情况下，对对方雷达实施有源压制干扰，掩护已方作战兵力实施武器打击［2～3］。本文主要研究了随队干扰和远距离支援干扰配合运用的方法，考虑到在对舰艇攻击完毕后转弯撤回时对方舰艇会处于己方干扰盲区内导致己方有被对方攻击的危险，故分两批次飞机相互配合来完成任务。第二批飞机次会在第一批次飞机转弯时对对方舰艇实施干扰以达到掩护第一批次飞机的目的，并通过仿真得出了第二批次飞机的最优飞行路线。

2 电子战飞机作战过程和队形

电子战飞机的作战过程分为抵近进攻、机动转弯和迅速撤回三个阶段。第一阶段，第一批次飞机向对方舰艇抵近飞行并发射导弹；第二阶段，第一批次飞机发射导弹后立即在第二批次飞机电子干扰的掩护下进行转弯撤离；最后阶段，第一批次飞机以最快的速度撤离。

电子战飞机在遂行随队干扰时，通常采用一架电子战飞机和两架对海战斗机相配合的组织形式，必要时还可加入一至两架担任空中掩护的战斗机，以应对对方可能派出的拦截机［5］。队形一般可采用电子战飞机在战斗机前约两公里的位置，两架战斗机分别在其两侧。这样在一定程度上可避免对己方飞机的误扰。

3 电子战飞机路径规划

3.1 干扰和撤退的路径规划

电子战飞机进行伴随干扰时应注意将被掩护战斗机时刻置于干扰扇面内［6］，在以混合编队进行作战时，可以两批次为一行动小组进行对海攻击。第一批次由电子战飞机与战斗机组成攻击梯队，第二批次可只配备一架电子战飞机负责掩护撤退。两批次飞机之间有一定间隔。第一批次的战斗机在电子战飞机的伴随掩护下以近似半椭圆的轨迹对对方军舰发起攻击，具体如图1所示。其中第一批次战斗机在进入导弹射程后对对方军舰发起导弹攻击，并立即以最小转弯半径进行转弯撤退［7～8］。并且第一批次飞机转弯之前的轨迹方向需朝向对方舰艇，目的是使电子战飞机的干扰波束主瓣对准对方舰艇进行干扰。同样的道理，转弯后的直线飞行也应尽量保持机尾对准对方军舰，以便其尾部干扰波束继续对准对方雷达干扰。

图1 发射导弹前两批次飞机示意图

当第一批次撤退时，随着飞机的机动转弯会使对方雷达位于飞机的干扰盲区内，致使对方军舰有了发现并攻击已方第一批次飞机的可能，所谓干扰盲区是指电子战飞机的干扰吊舱在首尾各存在大约60°的干扰角度范围，而在其他方向则无法进行干扰。为避免这种情况，第二批次电子战飞机的机头仍保持对准对方军舰进行电子干扰来掩护第一批次飞机。两批次之间的距离应满足在第一批次飞机转弯全过程中第二批次飞机始终对着对方军舰进行干扰［9］。设开始时两批次之间的距离最小为L1，转弯半径为R1，如图1所示，假设转弯时轨迹近似为θ0的圆弧，则有转弯时间：

式中，v1是飞机转弯时的速度。

式中，v2是电子战飞机直线飞行时的速度。

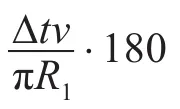
图2 第二批次飞机飞行轨迹示意图

图3 转弯时的雷达主瓣角度变化示意图

从t0起，tn时刻的

由余弦定理可得第一批次飞机与雷达的距离：

由正弦定理得：

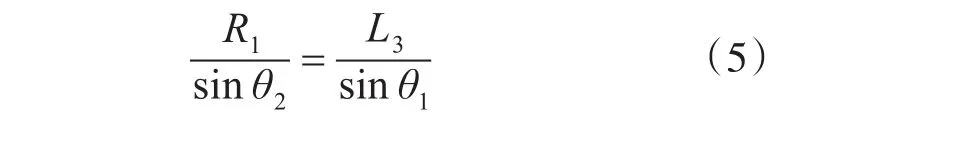
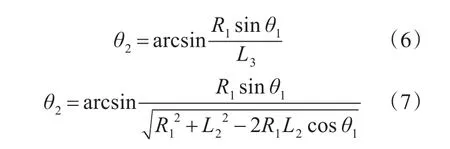
以上讨论了在弯道的前半部分θ2随时间的变化情况，后半部分以同样的原理作对称处理即可。因此，需使第二批次飞机对雷达的干扰扇面随时间的变化满足θ2随时间的变化。本文的目的是得到第二批次飞机的飞行轨迹，因此，需通过仿真求出图2所示以点画线为基准线与第二批次飞机轨迹夹角θ3的最优值。

3.2 干扰时的注意事项

1）干扰波束指向范围因素

在进行干扰时还应注意电子战飞机存在干扰角度范围，即约60°的波束指向范围。要达到干扰效果则必须使对方雷达处于己方干扰波束指向范围内。如图4所示雷达在干扰角度内，雷达会受到有效干扰；如图5所示雷达未在干扰角度内，则无法对雷达形成有效干扰。在仿真过程中，考虑到存在60°干扰张角范围，当第二批次飞机的飞行轨迹与基准线的夹角在0°～180°之间变化时会有对方雷达未能进入第二批次飞机的干扰张角范围的情况，因此仿真中得到了图2中所示第二批次飞机轨迹和第二批次飞机与雷达连线夹角θ4随第二批次飞机的飞行角度θ3变化。θ4应满足在 -30°～+30°的范围内。但是-30°～0°的部分不满足作战要求，因此仿真未考虑θ4在-30°～0°的情况。除此之外，还应注意合理高效地分配雷达干扰资源以提升作战效能［10］。

图4 雷达主瓣在干扰角度内

图5 雷达主瓣未在干扰角度内

2）干信比因素

在本文的仿真中，通过干信比来反映干扰效果。当干信比大于Kj时干扰有效。

干信比为

其中Pj为干扰机发射功率，Gj为干扰发射天线增益，γ0.5为极化失配损失系数，Pt为雷达发射功率，天线增益为Gt，σ为目标的雷达截面积，Rj（单位：m）为雷达与干扰机之间的距离，Rt（单位：m）为雷达与目标之间的距离，为雷达天线在干扰方向的增益，其取值满足如下关系：

其中θ0.5为雷达主辦宽度，θ为图6所示干扰机偏离雷达波束主轴的偏角［11～12］。

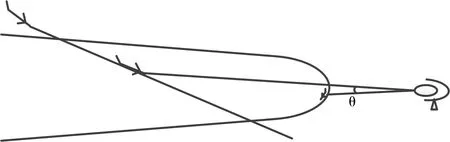
图6 干扰机偏离雷达波束主轴的偏角θ

4 仿真分析

4.1 参数设置

干扰机发射功率Pj=1kW，干扰发射天线增益Gj=20dB，极化失配损失系数γj=0.5，雷达发射功率Pt=250kW，天线增益Gt=40dB，采用式（9）的取值方法，其中θ0.5取2.5°，目标的雷达截面积σ=5m2，第一批次飞机的转弯半径取1km，对方雷达距转弯轨迹的圆心为50km。第一批次飞机飞行速度取1马赫，第二批次飞机飞行速度取1.5马赫。

在仿真中，将转弯轨迹近似为圆形轨迹，以其圆心为坐标原点建立模型，得到的仿真结果如下所示。

图7是第二批次飞机轨迹和第二批次飞机与雷达连线夹角θ4随飞行角度θ3变化的示意图。

根据上图仿真结果可得当第二批次飞机的飞行角度取30°时，对方雷达刚好处于干扰范围的边界，因此，在对干信比和相对波束张角进行仿真时要限制θ3的取值范围。为严谨起见，将θ3的取值范围作适当扩大。结果如图8、图9所示。

图7 θ4随飞行角度的变化关系

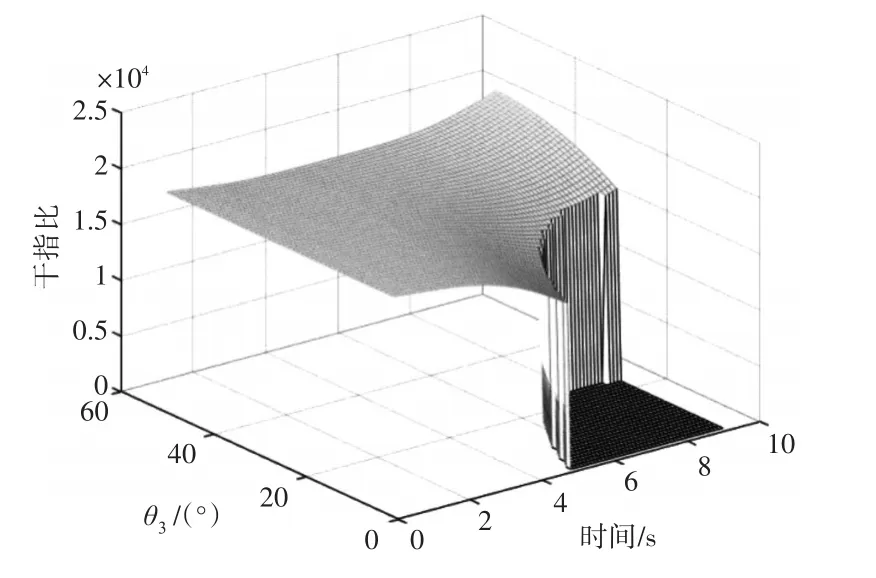
图8 干信比随时间和飞行角度的变化

图9 θ随时间和飞行角度的变化

4.2 结果分析

结合图7～图9所示仿真结果分析可知当θ3在0°～25°时，可以看到图8的干信比存在一个明显的陡降情况，干信比较其他区域明显变小，比较图9后不难发现在图8的干信比极小部分对应的区域刚好在图9中是角度差θ超过半波束宽度θ0.5的区域。表明当θ小于25°时，第二批次飞机存在大约5s的时间无法干扰到对方雷达主瓣，而只能干扰到副瓣，导致干信比急剧下降，干扰效果无法满足作战需求［13］。又由于存在干扰张角范围，根据图7可以看出，飞行角度θ3不能超过30°，否则会出现对方雷达未在干扰张角内的情况。所以最优飞行角度应在25°～30°之间取值。通过计算机分析图8中干信比的变化趋势并计算25°～30°范围内每个角度的干信比平均值可得出：在 25°～30°范围内，θ3越大，干扰效果越好。所以综上所述可以总结成以下几点：

1）干信比需不小于Kj。

3）夹角θ4不应超过 30°。

可得最优飞行角度应取27°或者说尽量接近30°为好。

5 结语

通过对作战过程的设计和仿真分析，可知分两批次的电子战飞机互相配合，可以很好地保证电子战飞机撤退过程中的电子战飞机和受掩护飞机编队的安全，避免短时间出现安全盲区造成受对方导弹攻击的危险。实际运用中要根据具体装备和飞机特性，合理计算和设计两批次飞机的飞行路径。