电气化铁路混合宽频滤波器研究

周福林，陈志远，熊进飞

（西南交通大学 电气工程学院,四川 成都 611756）

我国电气化铁路的电力机车和动车组（简称机车）,分别采用基于相控整流的交—直型传动方式和基于脉宽调制（Pulse Width Modulation,PWM）整流的交—直—交型传动方式。交—直型机车通过控制晶闸管触发角的大小调节直流侧电压,其特征谐波主要集中在3,5和7 次等低频段谐波；交—直—交型机车采用PWM 技术,虽输出的低次谐波减少,但开关频率附近的高次谐波增加,输出的主要谐波可广泛分布在20～100 次之间［1-5］。交—直型和交—直—交型机车共线混跑在未来较长一段时间内会长期存在,使得3～100 次宽频谐波将长期存在于牵引供电系统中［6］。运行实践表明,宽频谐波增加了谐波与线路发生共振的风险,易造成接触网和机车车顶的避雷器、互感器炸裂,线路补偿电容器、机车RC 电路损坏［7］,辅助供电系统直流电压抬升［8］,变电所低压电气设备损坏等故障［9］。

目前抑制电气化铁路宽频谐波主要从无源治理、有源治理、混合治理3个方面入手。在无源治理方面,应用于电气化铁路中的无源滤波器较多采用在地面安装单调谐滤波器［10］、2 阶高通滤波器［11］、阻波高通滤波器［12］,这对电气化铁路谐波谐振起到了较好的抑制效果,但只能对特定次或某一高频带的谐波进行治理,动态补偿性能较差,且易与牵引供电系统电源侧等效阻抗发生谐振；文献［13］提出了安装C型滤波器及C型与单调谐滤波器组合的2 种滤波方案,并从滤波效率、成本等方面评估这2 种方案的应用价值,但这2 种方案对系统参数很敏感,易与系统侧等效阻抗发生谐振；文献［14］提出将机车车载变流器网侧L型滤波器替换为LCL 型滤波器,通过辅以相应的控制算法抑制牵引网谐波谐振,但增加了机车的体积和重量,不利于车辆轻量化的发展要求。在有源治理方面,文献［15］提出使用有源电力滤波器（Active Power Filter,APF）完成对谐波的动态治理,APF 虽克服了无源滤波器的缺陷,但受开关器件容量和耐压的限制,难以适用于高电压、大容量场合；文献［16］提出采用降压变压器降低牵引网电压后接入APF,但变压器的引入增加了牵引供电系统的复杂性和相应的成本；文献［17-18］提出基于级联多电平技术的APF,能够适用于大容量、高电压的场合,但其拓扑结构和控制策略较为复杂。以上有源治理技术中,APF 难以跟踪高次谐波,因此难以对高次谐波进行治理。在混合治理方面,文献［19-20］提出有源与无源滤波器相结合的混合有源滤波器,其有源部分不直接承受基波电压,文献［19］中的晶闸管投切滤波器会阻碍有源部分发出的谐波电流,文献［20］中的基波谐振支路会使注入谐波分流,降低有源部分的补偿效率。以上混合治理技术主要以降低APF 承受电压为目的,其滤波范围在3～9 次谐波范围内。

本文提出在牵引供电系统地面变电所安装一种混合宽频滤波器（Hybrid Wideband-harmonics Filter,HWF）,HWF 由无源部分和有源部分构成,无源部分和有源部分分别对高次和低次谐波进行补偿。通过在有源部分前端添加基波谐振电路从而阻止基波电流通过,进而降低有源部分的基波电压；同时设置3,5 次谐波谐振电路避免有源部分发出的补偿电流被分流,确保有源部分补偿效率。最后通过仿真和试验验证HWF的可行性和有效性。

1 HWF拓扑结构

HWF 拓扑结构如图1所示。图中：US为牵引网电压；ZS为电源侧等效阻抗；iS为流过牵引供电系统系统侧的电流；iL为非线性负载（机车）产生的电流；iF为流过HWF 的电流；iB为流过阻波支路的电流；iC为APF 输出电流；红色实线框为有源部分,由APF、滤波电感L0和直流侧电容C2组成,通过电网整流的方式向C2充电以向APF 提供必需的直流电压Udc,有源部分的作用是补偿机车产生的低次谐波电流（次数＜7）；红色虚线框为HWF 的无源部分,由3 次谐波谐振电路（PRC3）、5 次谐波谐振电路（PRC5）、阻尼电阻R1组成的阻波支路及基波谐振电路（PRC1）构成,其中PRC1由电感L1和电容C1并联构成,PRC3和PRC5构成同理,无源部分的作用是补偿机车产生的高次谐波电流（次数≥7）,其中PRC3和PRC5分别调谐在3 和5 次频率处,用来阻碍机车电流中的3 和5 次谐波电流流过阻波支路,同时避免APF 发出的补偿电流被阻波支路分流,保障了有源部分对机车电流里面的3和5 次谐波电流进行有效补偿。

图1 HWF拓扑结构

此拓扑结构中,因为PRC1调谐于基波频率,PRC1在基波下呈现无穷大阻抗,所以基波电流基本不流过HWF,PRC1几乎承受全部基波电压,保证了有源部分不承受基波电压和电流,从而有效降低了有源部分的容量,在很大程度上克服有源部分的容量限制,更容易实现APF 在高压场合下的应用。

2 HWF滤波原理

HWF 谐波域等效电路如图2所示。图中：ZF和ZB分别为PRC1阻抗和阻波支路阻抗；iSh为流过牵引供电系统系统侧的谐波电流；iLh为机车产生的谐波电流；iFh为流过PRC1的谐波电流；iBh为流过阻波支路的谐波电流；UA为有源部分承受的电压。

图2 HWF谐波域等效电路

在图2中,根据基尔霍夫电流和电压定律可以得到

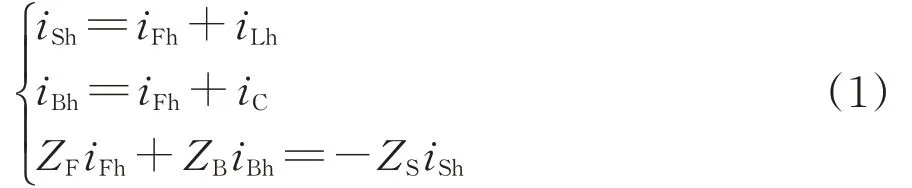
将APF输出电流控制为

式中：K为谐波补偿系数,K∈［0,1］；K=0 时,相当于只有无源部分工作；0＜K≤1时,相当于有源部分和无源部分共同工作。

由式（1）和式（2）可以解得

图2的等效电路如图3所示。从图3可以看出：HWF 的有源部分在谐波域等效为与电源侧等效阻抗ZS串联的阻抗KZB,当K值取最大时,将会有最少的谐波电流流入其系统；HWF 能够抑制无源部分阻抗与电网侧等效阻抗之间的谐振。

当K=0 时,即只考虑HWF 无源部分对高次谐波的滤波作用时,由式（3）可得

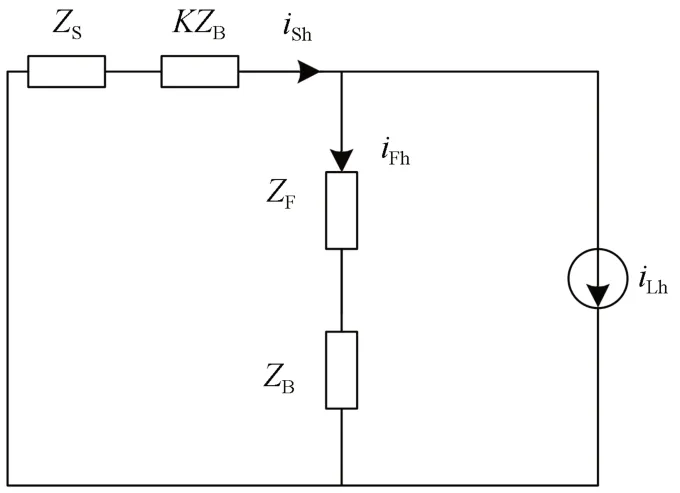
图3 图2等效电路

式（4）中,ZB+ZF为HWF 无源部分的阻抗,而从图1可以看出,因为有并联电容的存在,ZB+ZF在高次谐波下阻抗非常小,因而式（4）得到的iSh也很小,由此说明HWF 能够对机车产生的高次谐波电流进行有效滤除。

3 HWF特性分析

3.1 HWF滤波特性

为便于后文分析,先给出1 组HWF 无源部分的典型电气参数及系统侧等效电感LS参数见表1。

表1 无源部分跟系统侧等效电感的电气参数

利用Matlab/Simulink仿真软件对HWF无源部分阻抗进行仿真,结果如图4所示。从图4可以看出：HWF 的无源部分在高次谐波下阻抗非常小,能够对高次谐波电流提供滤波通路；同时,HWF无源部分有3 个并联谐振点,分别在50,150 和250 Hz 频率处,能够对基波电流和3,5 次谐波电流进行阻碍,以确保有源部分对机车产生的3,5 次谐波电流进行有效补偿。

3.2 HWF有源部分承受电压情况

HWF 无源部分由于PRC1的存在,导致基波电流无法流过HWF,根据基尔霍夫电流和电压定律,其中UA通过图2中红色箭头路径计算,可得

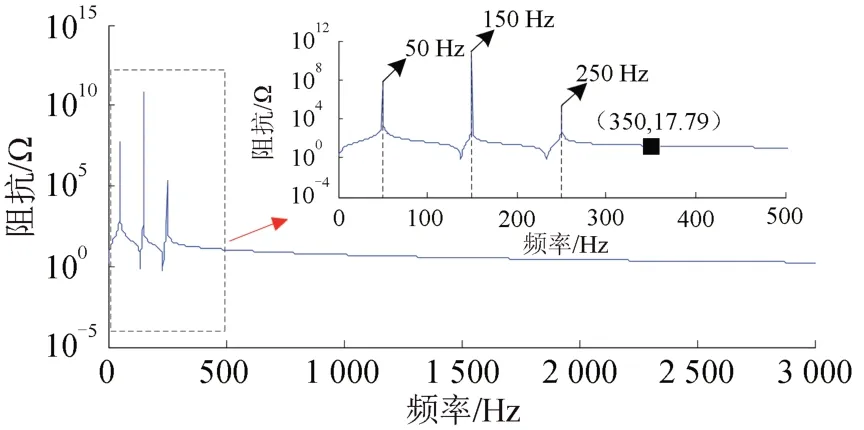
图4 HWF无源部分阻抗频率特性曲线

其中,

iSh=iFh+iLh

则APF承受的电压为

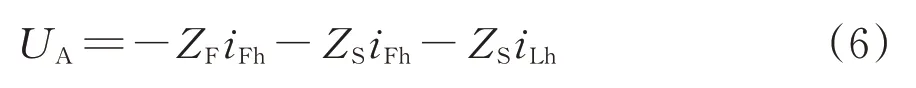
HWF工作在稳态时,流过HWF的谐波电流几乎与负载电流里面的谐波电流相等,即iFh=-iLh,则式（6）可以简化为

PRC1的阻抗频率特性曲线如图5所示。从图5可以看出：ZF在基波的时候很大,在低次谐波时相对较小；但是在高次谐波下,ZF变得非常小。因此,在高电压等级下,HWF 的有源部分主要承受低次谐波电压。

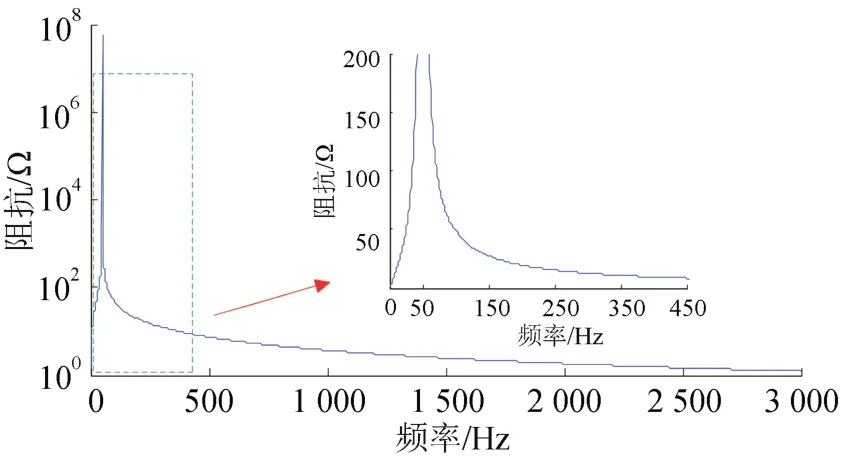
图5 PRC1阻抗频率特性曲线

3.3 谐波补偿系数K对HWF补偿特性的影响

为了验证K值对HWF 补偿性能的影响,定义流过牵引供电系统系统侧的谐波电流iSh与流过机车谐波电流iLh之比为HWF 的谐波抑制能力函数,则

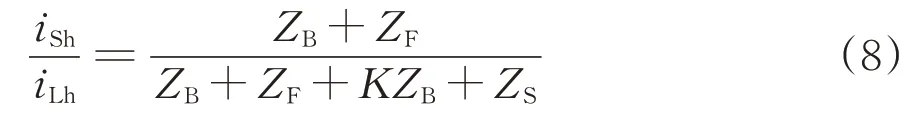
假设电源侧等效阻抗为

式中：j为虚数单位；ω为角频率。

因HWF无源部分由PRC1和阻波支路组成,则

用拉普拉斯算子s替换式（8）—式（11）中的jω可以得到复频域中HWF 的闭环控制框图如图6所示。图中：A=ZF（s）/ZB（s）,B=ZS（s）/ZB（s）。

图6 HWF闭环控制框图

由图6可知HWF的闭环传递函数Gcolse（s）为

其中,

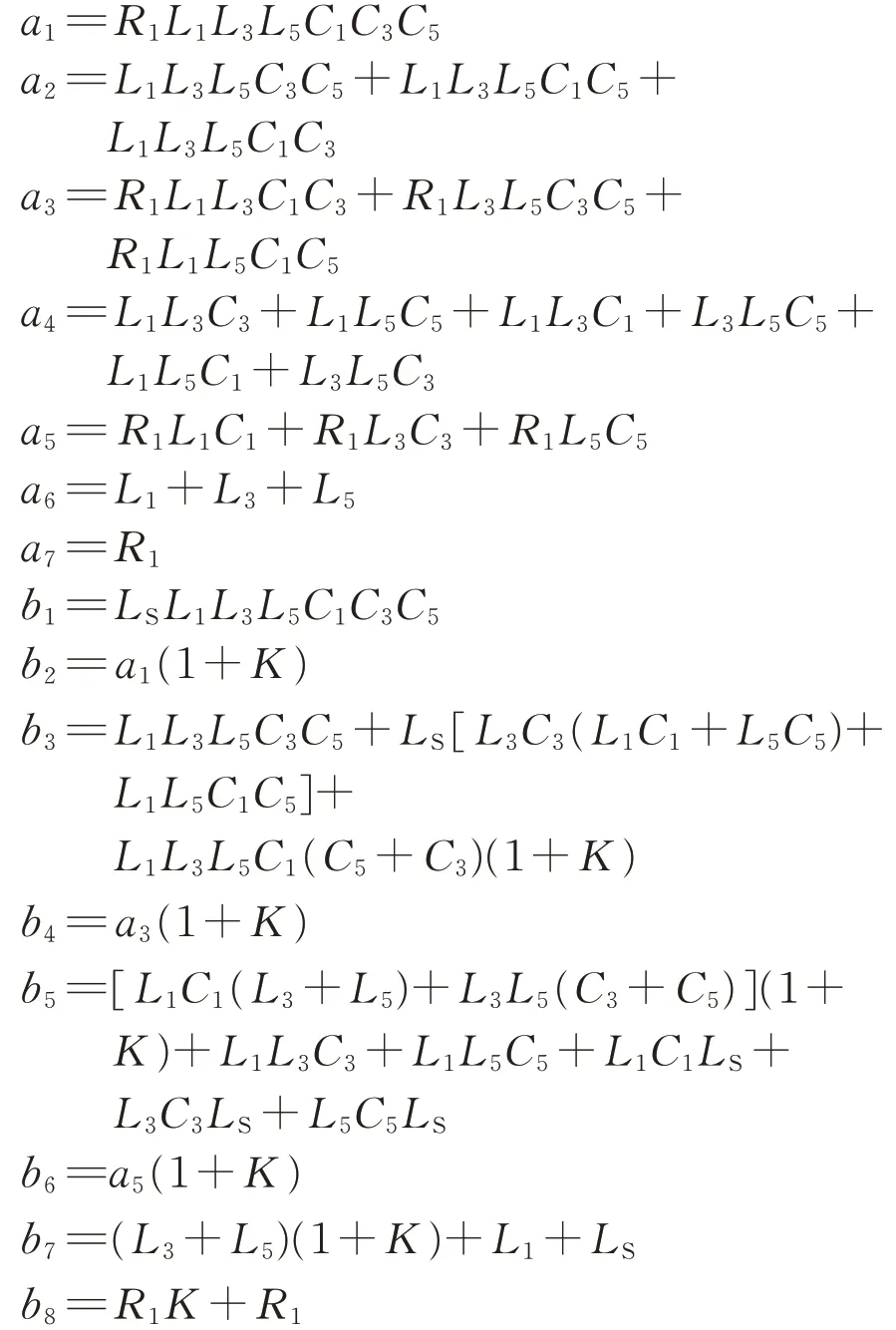
结合式（12）,当K值分别取0,0.2 及1.0 时HWF闭环传递函数的幅频特性曲线如图7所示。

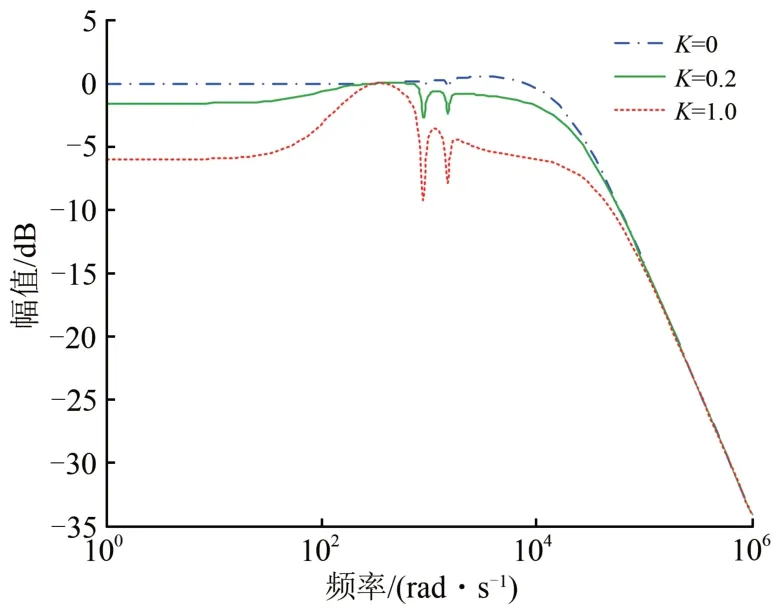
图7 不同K值时HWF闭环传递函数的幅频特性曲线

从图7可以看出：K=0 时,相当于只考虑无源部分的补偿作用,此时HWF 对高次谐波有较大的抑制作用,在ω=103～104rad·s-1之间时,HWF 的闭环传递函数增益大于0,但增益并未出现明显的谐振峰值,由此说明HWF 的无源部分与系统侧等效阻抗之间不会产生谐振；K≠0 时,相当于有源部分投入,HWF 的闭环传递函数的幅频特性在所有的频率段都往负半轴移动,此时HWF对各次频率的谐波都能起到有效的抑制效果。因此,在一定范围内,K值越大,HWF 对谐波的抑制效果越好。

3.4 HWF稳定性

由式（12）可知,HWF的特征方程为

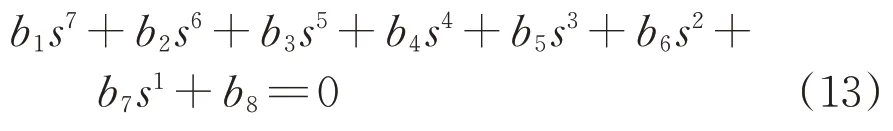
因式（13）的阶次较高,该解难以直接求出,故采用劳斯判据分析HWF的稳定性。其闭环特征方程的劳斯表见表2。表中,A1=(b2b3-b1b4)/b2,B1=(A1b4-b2A2)/A1,C1=(B1A2-A1B2)/B1,D1=(C1B2-B1C2)/C1,E1=(D1C2-C1D2)/D1,F1=D2。

表2 闭环特征方程的劳斯表

由劳斯判据可知,系统稳定的充要条件是式（13）的所有系数b1—b8均为正数,且表2左数第1列的各个值也必须为正数。而式（13）的系数b1—b8本身即为正数,所以只要A1,B1,C1,D1,E1和F1均为正数即可,由此可得

分别将表1中的参数和代入表2所示的劳斯表中,发现式（14）恒成立,说明K值会影响HWF对谐波的抑制能力,但不会影响HWF的稳定性。

4 HWF控制策略

谐波电流检测电路采用单相任意次谐波电流检测［20］,如图8所示。图中：sin（kωt）和cos（kωt）为通过锁相环（PLL）得到的频率为牵引网基波电压k倍的单位正余弦信号,k取3 和5；LPF 为低通滤波器。

图8 仿真结构图

由于三角载波控制具有固定的开关频率,动态响应好的优点［21］,因此仿真时采用三角载波控制的方法,将APF 输出的实际补偿电流iC与检测的指令电流iC*的差值送入PI 调节器,将调节结果uC作为调制波,通过对三角载波进行调制得到PWM波,驱动APF输出期望的补偿电流。

5 仿真及试验验证

5.1 仿真结果

为验证HWF 在牵引供电系统中对宽频谐波治理的有效性和正确性,在Matlab/Simulink 仿真软件中根据图8搭建仿真模型。其中包括220 kV 外部系统电源、V/x 牵引变压器、牵引网、1 个AT所、1 个分区所、电力机车、HWF 等。牵引网为AT 全并联运行方式,由上行的接触线T1、钢轨R1、正馈线F1、加强导线P1、下行的接触线T2、钢轨R2、正馈线F2、加强导线P2构成,其中Yp和Zp分别为线路π 型等值电路的等值阻抗和等值导纳［22］。机车采用四象限运行的整流器模型等效,能够产生低次和高次谐波电流,运行于距离牵引变电所15 km处。HWF的有源部分被控制为谐波电流源,其中K=1,L0=25 mH,直流侧电压为2 kV。牵引供电系统仿真参数见表3。

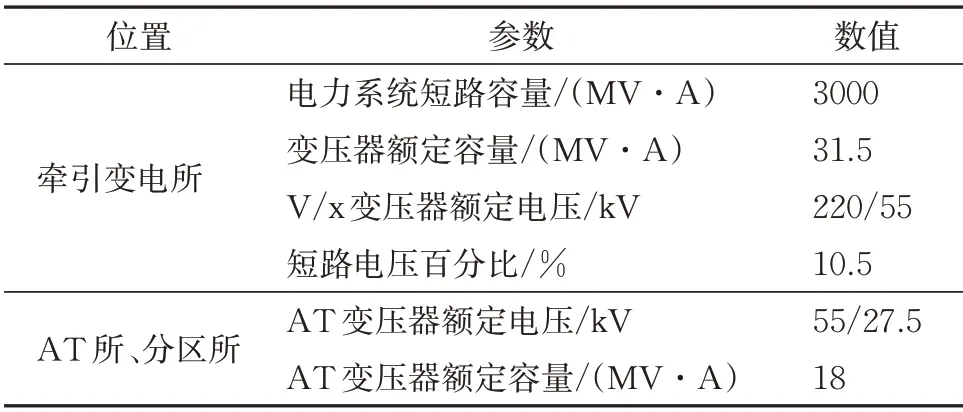
表3 牵引供电系统仿真参数

牵引供电系统系统侧电流波形如图9所示,其中HWF 的无源和有源部分分别于0.04和0.10 s时刻投入工作。图9中所示各个阶段系统侧电流的频谱图如图10所示。

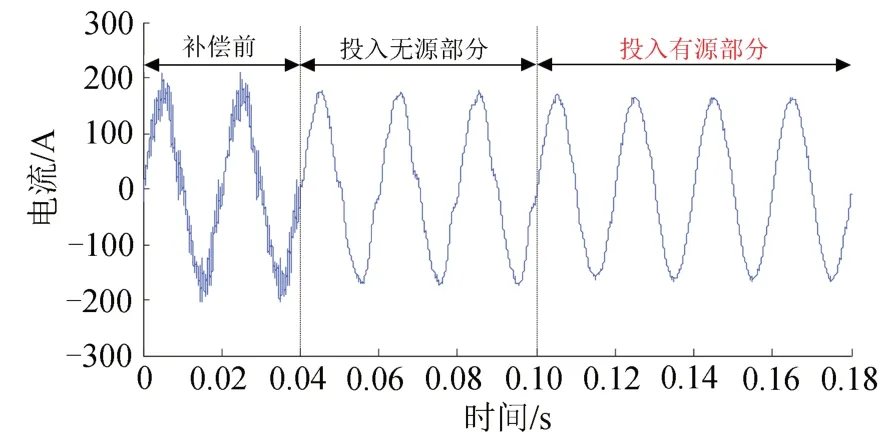
图9 牵引供电系统系统侧电流波形

图10 各个阶段系统侧电流的频谱图

由图9和图10可以看出：补偿前,牵引供电系统系统侧电流含有低次和高次谐波成分,此时的电流总谐波畸变率（Total Harmonic Distortion,THD）为18.57%,电流波形畸变严重；而当无源部分投入工作后,牵引供电系统系统侧电流的高次谐波成分经无源部分滤除后,只含有低次谐波电流成分,此时电流THD 由原来的18.57%降为10.67%；在0.10 s时刻投入有源部分后,此时系统侧电流里面的低次谐波被有源部分补偿,电流THD 降为2.41%,且系统侧电流波形有很高的正弦度。

牵引网电压波形如图11所示。由图11可以看出：补偿前,牵引网发生了谐振,牵引网电压波形畸变严重；而当HWF 投入运行后,牵引网电压波形有很高的正弦度。

图11 牵引网电压波形

有源部分承受的电压及其频谱图如图12所示。由图12可以看出：相比较于27.5 kV 的牵引网电压,有源部分承受的电压不超过1 000 V（瞬时值）,有源部分承受的电压大幅度降低；同时对比图12（a）和图12（b）,可以验证如前3.2 节所述的有源部分基本不承受基波电压、主要承受低次谐波电压的特点。因此,HWF 适用于中高压电力系统宽频谐波的治理。

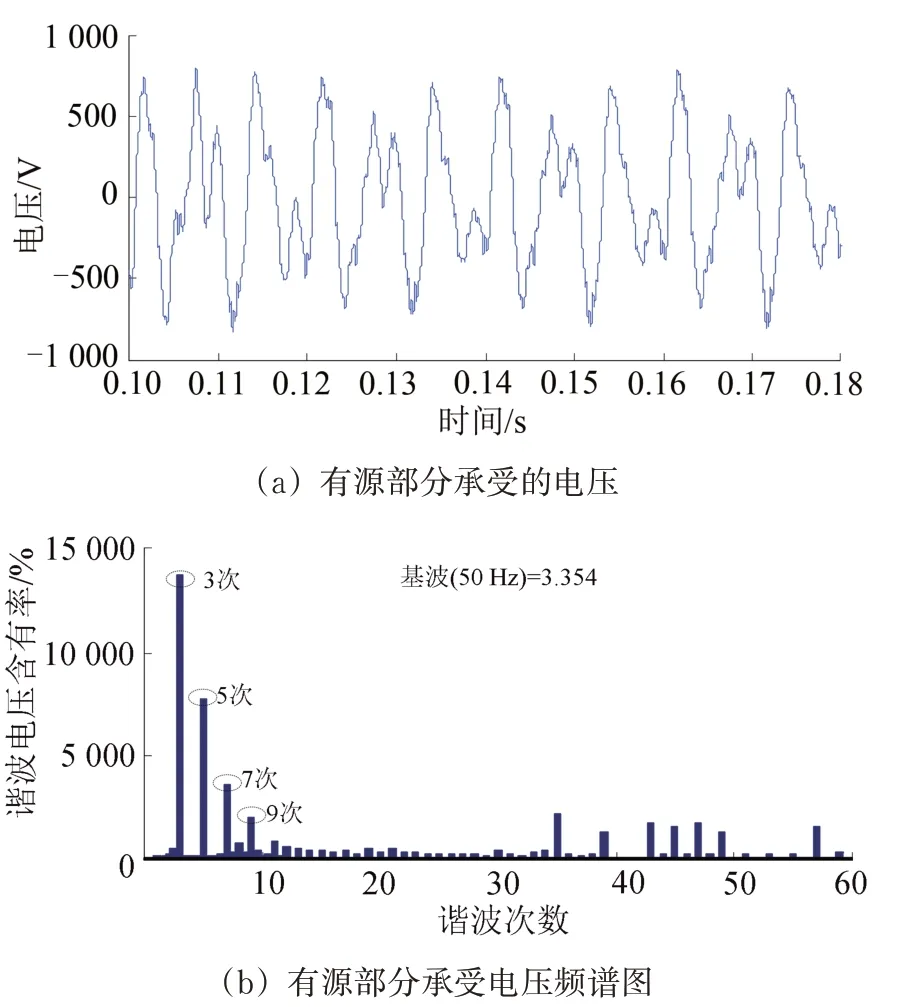
图12 有源部分承受的电压及其频谱图

5.2 试验结果

为进一步验证HWF 对宽频谐波的滤波性能,根据图1所示的单相等效电路建立试验平台。控制器硬件选用Altera 公司的第3 代FPGA 芯片EP4C10F17C8N。谐波源为二极管整流桥,其电阻负载初始为20 Ω（突变至10 Ω）,试验系统参数见表4。

将表4中的参数代入表2中,式（14）恒成立,说明试验系统稳定。电阻负载从20 Ω 突变为10 Ω时的试验波形如图13所示。从图13可以看出,负载突变前后,试验系统系统侧电流一直都为正弦波,说明HWF具有很好的动态补偿效果。

表4 试验系统参数

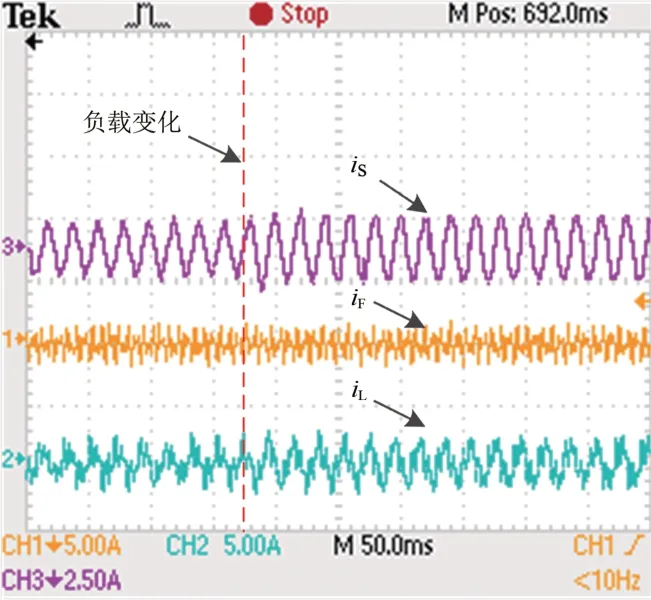
图13 电阻负载从20 Ω突变为10 Ω时的试验波形

HWF 稳态运行时的试验波形如图14所示。从图14可以看出：有源部分主要承受低次谐波电压,且相比较于系统电压US有所降低。

图14 HWF稳态运行的试验波形

HWF 补偿前后试验系统系统侧电流频谱图如图15所示。从图15可以看出：补偿前,系统侧电流THD 为20.0%,主要含有3 和5 次谐波电流分量；补偿后,系统侧电流THD 为2.5%,特征次谐波电流得到充分衰减。

图15 HWF补偿前后试验系统系统侧电流频谱图

6 结 论

（1）混合宽频滤波器HWF 能够大大改善无源部分的谐波补偿性能,能够对宽频谐波电流进行良好的补偿；同时,HWF 能够很好地抑制无源部分阻抗与电网阻抗之间的谐振。

（2）基波谐振电路PRC1设计的目的是用来承受高电压,降低HWF 的有源部分承受的基波电压；有源部分只补偿系统侧电流的低次谐波成分,这样可以有效降低有源部分容量,使得经济性更高。

（3）3次谐波谐振电路PRC3和5次谐波谐振电路PRC5能够阻止3次和5次谐波电流跟有源部分发出的3 次和5 次谐波电流流过阻波支路,保证HWF有源部分的补偿效率。