求解公共自行车再平衡问题的克隆选择算法

刘喜梅，潘立军

湖南工程学院 管理学院，湖南 湘潭411104

1 引言

公共自行车再平衡问题（Bike Sharing Rebalancing Problem，BRP）是一类NP-难问题[1]。其可描述为利用有相同载重的车辆从单车维护补给中心出发完成一定区域内各单车停放点自行车的再分配，使各停放点达到预先设置容量后回到中心，如何使所有的车辆行驶的距离或花费的时间成本最少。20 世纪60 年代，公共自行车系统最早在荷兰阿姆斯特丹出现，随着社会经济的不断发展，特别是交通拥堵、环境污染等城市问题不断突显，公共自行车作为健康、环保、便捷的出行方式逐步在世界各地普及。目前，全世界约有49个国家共计超过500个公共自行车系统，如法国巴黎（20 600 辆）、中国杭州（78 000 辆）、中国武汉（90 000 辆）、中国株洲（20 000辆）[2]。公共自行车系统的普及使各地公共自行车运营部门单车再平衡任务加剧，通常公共自行车运营公司组织自有运输车辆从维护补给中心出发，按照事先各停靠点分配单车取送量依次访问各停靠点，再回到维护补给中心，在该过程中，运输车辆既可以在各停放点间调配自行车，也可在出发前从维护补给中心载入一部分自行车调配到各停放点，或将各停放点多余的自行车运回维护补给中心。

国外有关公共自行车再平衡的研究报道目前主要关注二类BRP，一是静态BRP[3-9]，即在车辆开始服务各停放点后，各点平衡数量不发生变化，如在夜间（22点至第二天凌晨6点间）用户几乎不使用自行车的时段进行再平衡作业；二是动态BRP[10-12]，即在车辆开始平衡作业服务后，各停靠点单车平衡数量依旧发生变化，如在公共自行车使用频率较高的区域，再平衡期间仍有用户用车。从BRP的问题特点来看，求解目标有最小化车辆行驶费用[11]、最小化再平衡总费用（该费用包括车辆运输费用、装卸单车费用）[10，12]、最小化作业时间[3-8]、最大化客户满意度（满意度表示为站点初始单车保有量与用户取还车频率的函数，用户在站点取还车失败的可能性越高，满意度越低，反之则越大）[9-10，12]。从BRP求解方法来看，目前报道较多的主要有三类，一类是精确算法，如分枝定界法[3-5]；二是各类经典启发式算法，如节约算法[6]、贪婪算法[7]，可变邻域下降搜索[8]等；三是智能启发式算法，如禁忌搜索算法[9]。表1 对国外主要的研究报道进行了梳理总结。

我国虽然是公共自行车保有量最大的国家，但目前国内公共自行车再平衡的研究报道比较少，白雪等[13]研究了考虑维修车辆的公共自行车系统再平衡问题，提出了基于动态规划的精确算法。前期也对求解BRP的遗传算法[14]进行了研究，运用标准算例测试表明其具有较好的求解效率。此外，叶丽霞[15]、乔晓[16]对我国南京市江宁区、西安市雁塔区的公共自行车再平衡作业进行了案例研究。

综合分析来看，国外对BRP 的研究起步早，成果较多，对BRP问题特点及精确算法、经典启发式算法作了较深入的研究，但应用智能启发式算法求解BRP的研究比较少，尚没有求解BRP的人工免疫克隆选择算法的报道，而国内研究多为案例研究，研究成果难以推广应用，因此均不适合开发具有一定通用性的计算机调度软件来辅助公共自行车系统再平衡。在实践中，公共自行车的再平衡是一项周期性的调度工作，用户的用车行为具有惯性（即一段时间内各停靠点取车、用车数量不会出现剧烈波动），前一天的再平衡调度方案对第二天的调度方案优化具有重要的参考价值。

人工免疫算法是模仿生物免疫系统的一种智能优化方法。生物免疫系统通过构建具有动态性、自适应性和自组织性的信息防御系统，以此来抵御外部无用、有害和干扰信息的侵入，从而保证系统接受信息的有效性与无害性。代表性的人工免疫算法是巴西人工免疫学专家Castro 等人[17]借鉴生物免疫系统的克隆选择原理提出的克隆选择算法，该算法通过模拟生物免疫系统的对抗原初次免疫应答和二次免疫应答机制，能较好地处理优化求解中基于过往方案优化现有方案的场景[18]，作为一种全局性邻域搜索智能启发式算法，在处理NP-难问题时有较好效果，Kim[19]与Coello[20]分别运用该方法处理了多目标的数值优化问题，文献[21]则运用该方法求解带工作时间与时间窗的开放式车辆路径问题，均显示出较好的求解效果。

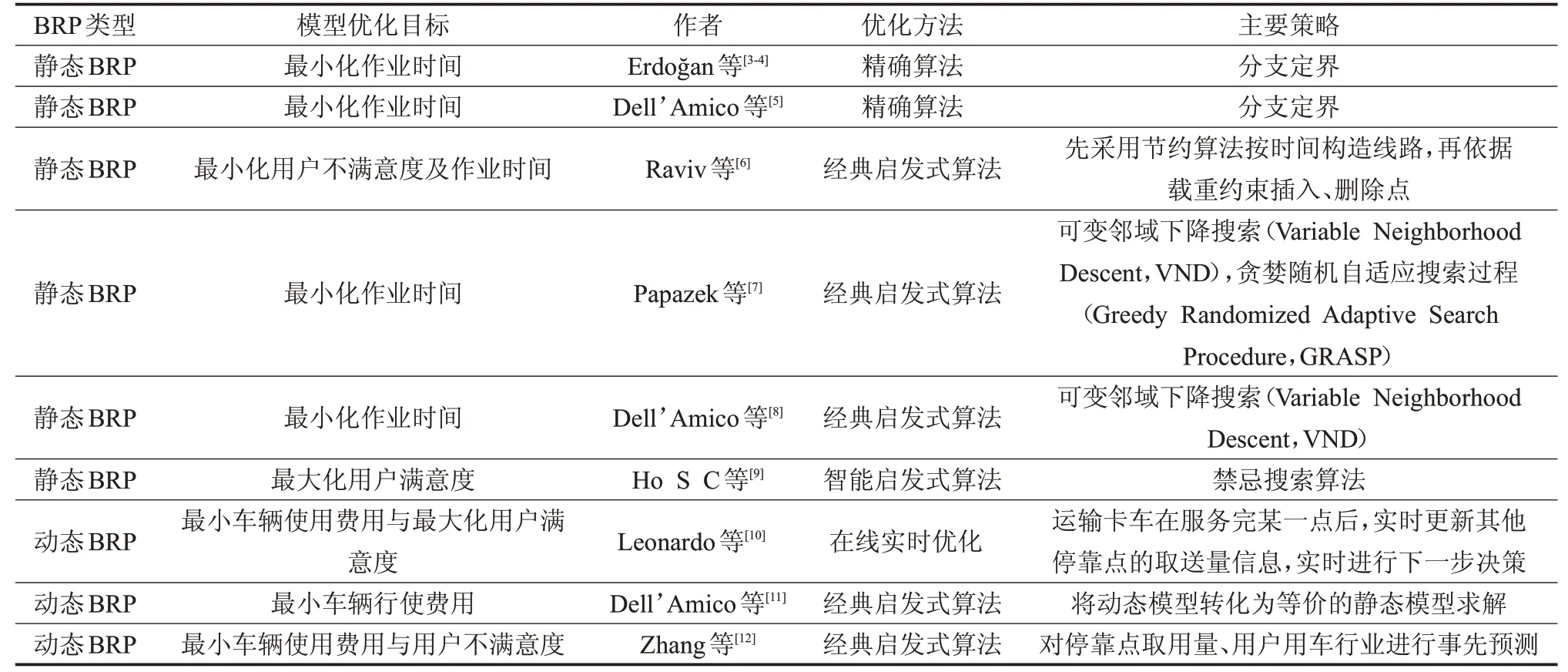
表1 国外BRP研究代表性文献

2 BRP数学模型

借鉴文献[5]，BRP 的数学模型表示如下：设有一完备图G=(V,E)，V={1,2,…,n}表示顶点集，其中1表示自行车维护与补给中心，V′ {2,3,…,n}表示单车停放点集，E={(i,j)|i,j ∈V,i ≠j}表示弧集或边集。其符号定义为：M 表示实施再平衡运输的专用车辆数；Q表示专用运输车辆的最大载重量，di表示车辆在第i 个单车停放点取送量，di的取值范围为[-Q,Q]，di小于0，表示该停放点需补充单车，di大于0，表示该停放点要回收单车；cij表示专用车辆访问弧(i,j)产生的运输成本或时间；θj表示专用车辆访问第j 个停放点后的载重量，即车辆线路载重量。决策变量xij=1，表示车辆访问了弧(i,j)，否则，xij=0。

式（1）为目标函数，为最小化运输总成本或时间，式（2）、式（3）确保除维护补给中心点外其余单车停放点均被访问且只访问一次，式（4）、式（5）确保所有的专用运输车辆在完成任务后均回到维护与补给中心，式（6）为消除子回路约束，式（7）、式（8）、式（9）为BRP车辆载重约束，确保各专用运输车辆在实施单车回收与投放过程中，车辆线路载重量不超过额定载重量，其假设在某一停靠点回收的自行车可被投放到任意其他需要的点，且车辆出发或者回到补给中心时，载重可不为零，因为可以事先装入部分单车，或者带回部分单车。

3 求解BRP的克隆选择算法

3.1 算法主要框架

求解BRP 的克隆选择算法基本步骤如图1 所示。其中抗体的编码方式采用多维整数编码方法[14]，初始解生成借鉴文献[22]的方法，采用随机选择停靠点、插入位置插入。算法的终止条件设定为迭代次数Max_iter或当前最优解连续不改进的次数Max_Not_Improve 达到事先设定的常数。

图1 克隆选择算法基本流程图

算法运行中设定了一定容量的记忆细胞群体Memory，算法每迭代100 次，将抗体群中的最优抗体存入Memory，算法终止后，从当前Memory 输出最优抗体。当有新的问题求解时，也可直接从Memory 中选取一定数量的记忆细胞，直接计算是否满足新的问题约束条件，若满足，可直接计算抗体与抗原的亲和力，进入算法后续步骤迭代，其过程如图1 中虚线部分所示，这部分反映了人工免疫系统中特有的二次免疫应答机制，即当有新的抗原侵入免疫系统时，可直接借助成熟的记忆细胞展开免疫应答，以达到快速形成免疫能力的目标。

在实践中，由于部分公共自行车用户需求以通勤出行为主，因此公共自行车各停靠点的再平衡量作业量在相邻的几天内变动较小，前一天的再平衡调度方案对形成新的再平衡调度方案有重要的参考价值。同时分析BRP模型来看，约束条件式（9）为两不等式，表明可行线路中车辆通过每点的装载量有一定的变动空间。因此，在克隆选择算法中引入二次免疫应答机制对提升算法求解效率有帮助。

3.2 亲和力定义与克隆选择算子

在本文算法中，求解目标为使目标函数式（1）最小。因此将抗原与抗体的亲和力定义为目标函数式（1）的倒数，即目标函数值越小，则该抗体与抗原的亲和力越大。

克隆选择算子设计参考文献[21]的方法，主要有以下两步：

步骤1 计算当前抗体群中每个抗体与抗原的亲和力，并按亲和力降序排列。

步骤2 按照下式对种群中亲和力高的抗体进行克隆，得到新的抗体群Nc：

式中，Scale 代表抗体群的规模，Pos 表示抗体群在降序排列后该抗体在群中的序位，Pos 为整数且满足：0 ＜Pos ＜；Nc代表克隆后新的抗体群，Nc ＞Scale；β 为克隆系数，其取值区间为：0.2 ＜β ＜0.3。

3.3 变异算子

抗体经过克隆后则经历高频变异，高频变异是克隆选择算法进行邻域搜索的主要手段。本文采用混合邻域结构，即随机选择点对操作对当前解的邻域进行搜索，设计了以下五类变异算子。为了便于说明，设S1=（1356 147928），编号1 代表维修保养中心，选取进行变换的点对为i=5,j=9，具体变换方法如下：

（1）顶点前向重新指派

将所挑选的顶点i 从线路上当前的位置中取出，并将其插入到所挑选顶点j 的位置之前。例如：S1=（1356 147928）→S2=（136 1475928）。

（2）顶点后向重新指派

将所挑选的顶点i 从线路上当前的位置中取出，并将其插入到所挑选顶点j 的位置之后。例如：S1=（1356 147928）→S2=（136 1479528）。

（3）顶点交换

将所挑选的顶点i、j 交换位置。例如：S1=（1356 147928）→S2=（1396 147528）。

（4）尾巴交换

若所挑选的两个顶点i、j 位于不同的线路上，则将所挑选的两个顶点后面的“尾巴”（从被选顶点至线路末尾）互换。例如：S1=（1356 147928）→S2=（13928 14756）。

（5）2-opt

若所挑选的两点i、j 位于同一条线路上，则将i、j两点间所有顶点的排列顺序逆转。若所挑选的两点i、j 位于不同线路上，则执行以下四种变换：变换1，S1=（1356 147928）→S2=（13829 14765）；变换2，S1=（1356 147928）→S2=（139741 6528）；变换3，S1=（1356 147928）→S2=（97416 53128）；变换4，S1=（1356 147928）→S2=（8296 147531）。

以上几种变异方法随机采用，且为兼顾算法搜索的质量与速度，算法前期（当前迭代次数＜Max_iter/2）时采取随机变异，即变异后的抗体可行，且与原抗体目标值不同即接受变异，后期（当前迭代次数≥Max_iter/2）时采取寻优变异，即每种变异取不同的点对执行5 次，若变异后的抗体可行，且亲和力优于原抗体，则接收变异。

3.4 抗体相似性定义与抗体抑制

为进行抗体抑制，定义抗体相似性Lxy的度量方法如下：

设x 与y 为同一抗体种群中两个不同抗体，p 为抗体边矩阵（n 维方阵，n 为完备图G 中顶点数量），若抗体x 中有边E(i,j)，则=1，否则为0(i,j ∈V,i ≠j)。

式（11）中，函数sum(p)的功能为计算抗体边矩阵中各元素之和，若抗体x 与y 完全相同，则其边矩阵px=py，则Lxy=0；若抗体x 与y 完全不相同，则Lxy=1。

抗体群经历克隆与高频变异后，产生了一些亲和力低或与其他抗体结构相近的抗体，通常抗体抑制过程即将这些抗体从种群中删除并补充新的抗体到原抗体群中，该过程有利于增加算法的搜索区域，避免算法陷入局部收敛。本文抗体抑制的具体步骤如下：

步骤1 定义抗体相似度系数λ ，其取值范围为[0.3，0.6]。

步骤2 计算抗体与抗原的亲和力，按亲和力降序排列，得抗体群Pop(a1,a2,…,aNc)，Nc 为抗体群规模。

步骤3 将a1加入新的抗体群Popnew。

步骤4 从a2开始，依次将Pop 中的抗体与Popnew中当前抗体比较，若相似度小于等于λ，则将其加入到Popnew中，直到Popnew的规模达到Scale，若Pop 中的抗体数量不足，则从记忆细胞库中选择记忆细胞加入，若还不足，则生成新抗体加入到Popnew中。

4 算法测试

算法采用matlab2014 编程实现，运行于CPU（core i3，3.1 GHz）、ROM（4 GB）的PC机上。

4.1 初次应答求解效率测试

首先运用BRP标准测试算例，测试人工免疫克隆选择算法初次应答求解效率，主要参数设置为：变异概率取0.9，种群规模Scale=50,β=0.3,λ=0.4 ，最大循环次数Search_Max 为4 000，Not_Improve 为800。每个算例运行10 次，取最好解与平均运行时间。将本文算法与分支定界法（B&C）[5]、遗传算法[14]进行比较（三种算法的测试硬件环境基本相同）。

表2、表3 中，Si代表各算法的求解结果，CPUi表示各算法求解CPU消耗，N/C 分别代表算例的停靠点数量与运送卡车额定载重量，g_B&C=(S2-S1)/S2、g_GA=(S3-S1)/S3，表示本文算法相较于B&C、GA 在求解质量上的差距，g_t_B&C=(CPU2-CPU1)/CPU2、g_t_GA=(CPU3-CPU1)/CPU3，为本文算法相较于B&C、GA在求解时间上的差距。（1）在规模小于50个点算例上，本文算法能找到所有算例的当前最好解，平均CPU 消耗为9.6 s，比B&C 的快96.80%，但比GA 慢，如表2所示；（2）在规模为50至100个点的算例，本文算法找到6 个算例的最优解（表3 中加粗表示），平均求解质量比B&C 低7.43%，但比GA 高1.02%，平均CPU 消耗相较于B&C快96.8%。

4.2 算法二次应答的求解效率测试

为了测试人工免疫克隆选择算法二次应答的求解效率，本文对BRP 标准测试问题Roid(N=55/C=20)的停靠点取送车量（d）进行修改，生成3组新的测试问题，用以模拟不同场景下公共自行车运营系统连续两天的再平衡需求。修改方法为：分别取p=1、2、3，随机选取Roid 中80%的停靠点，对原停靠点取送单车数量按d±p 进行修改（p 的正负号随机选取，但需确保新的停靠点取送车数量不等于0），每组算例生成4个新的问题。算法测试的参数设置除Not_Improve=400 外，其他参数设置与第一部分测试相同。二次应答测试方法为算法先运行Roid问题，并将求解过程中的记忆细胞保存，再分别运行改进后的测试问题，记录运行结果及CPU消耗。

测试算例Roid中各点再平衡车辆数的取值区间为[-7，7]，表4～6分别模拟测试连续两天内，再平衡量变化幅度为14.3%(p=1)、28.6%(p=2)、42.9%(p=3)的情况下，算法二次应答效率。测试结果表明：二次应答的求解质量分别比一次应答的高0.65% (p=1) 、0.24%(p=2) 、0.16% (p=3) ，CPU 消耗比一次应答分别快39.78%(p=1)、46.18%(p=2)、40.66%(p=3)。表4～6中：g_32=(S1-S2)/S1,t_32=(CPU1-CPU3)/CPU3。

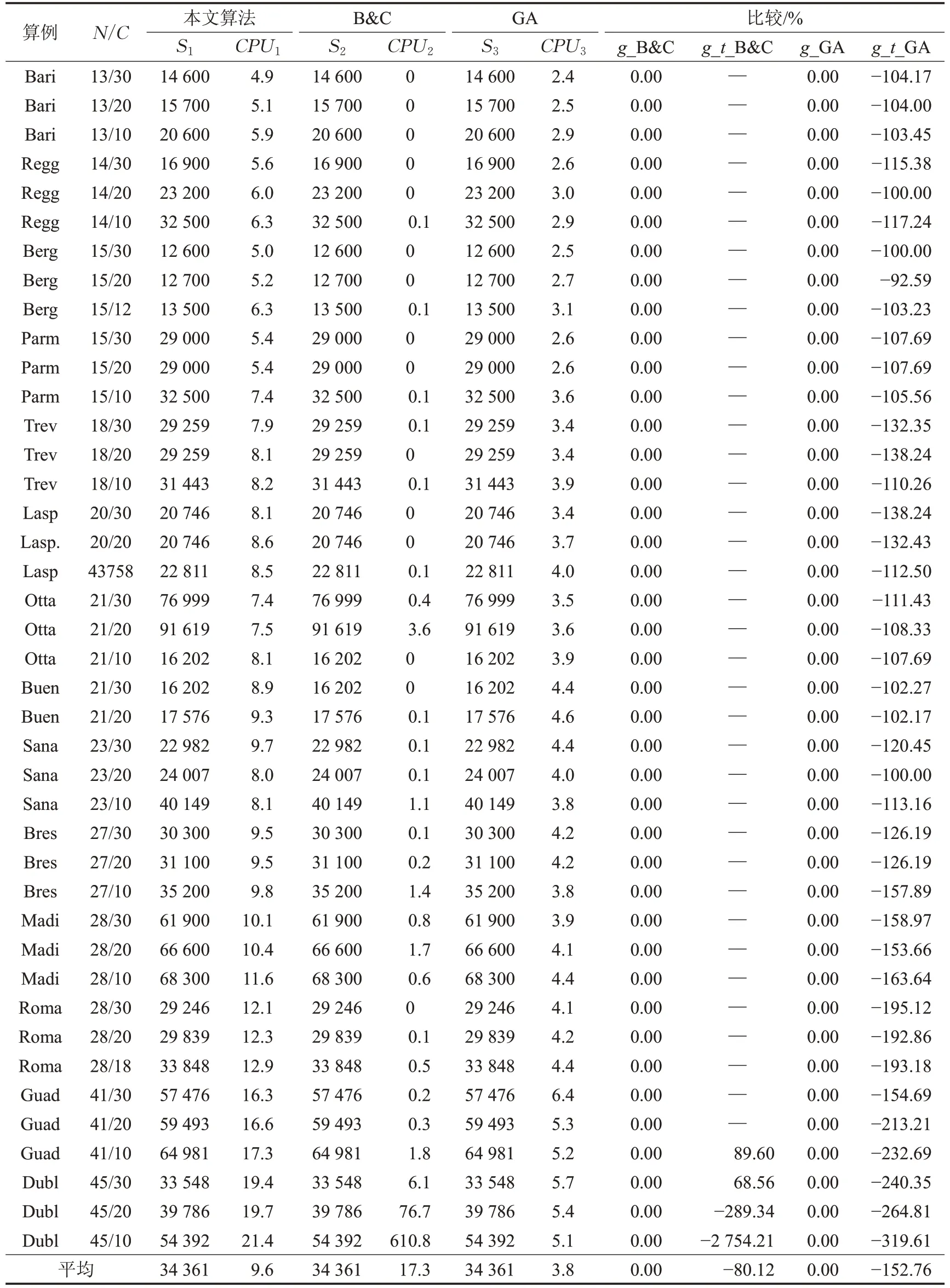
表2 小于50个点的算例测试结果

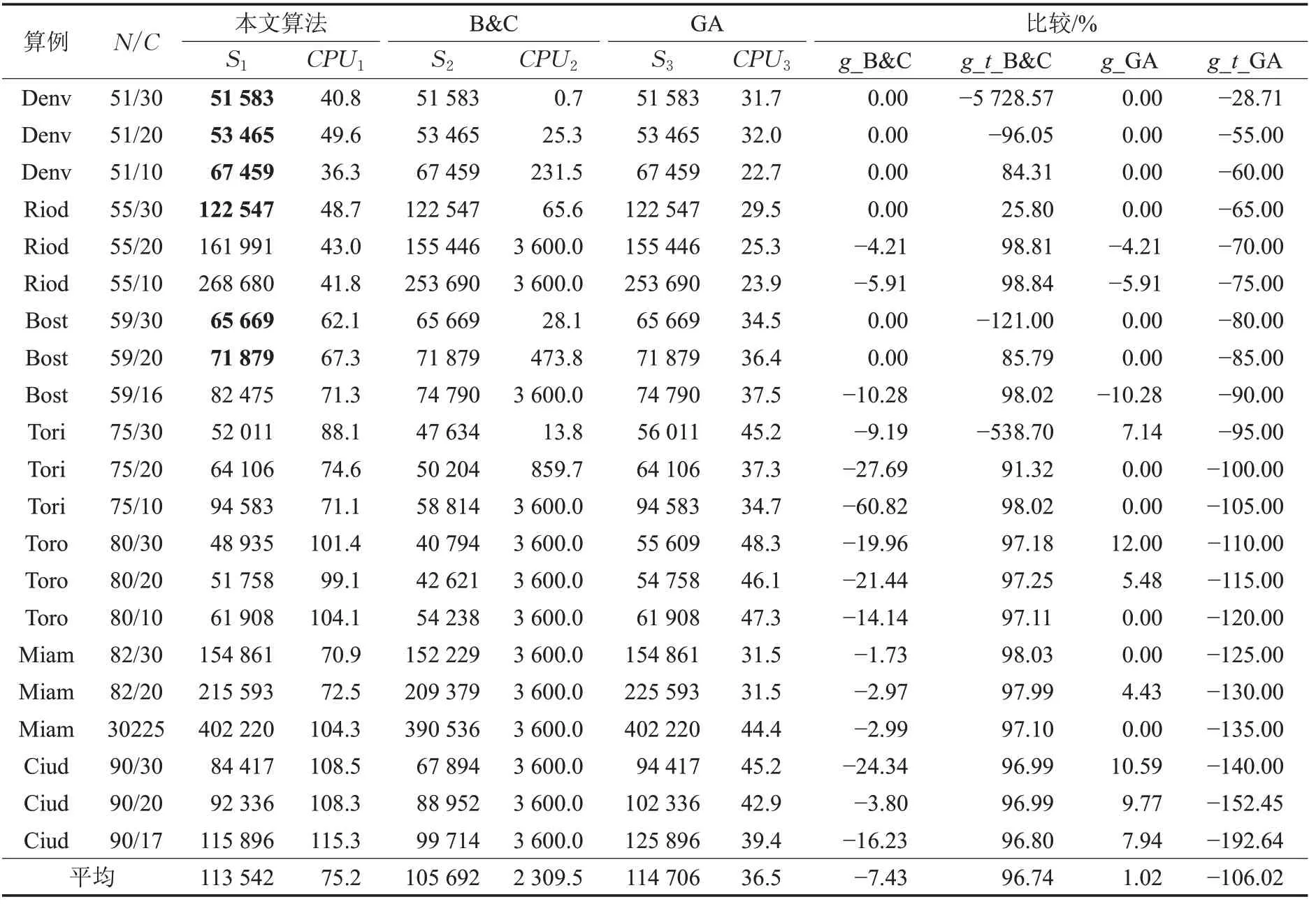
表3 大于50个点小于100个点的算例测试结果

5 结束语

公共自行车系统在我国普及度高，系统的再平衡调度方法研究有着非常广泛的应用价值。本文在已有研究基础上，设计了求解BRP的人工免疫克隆选择算法，算法采用多维整数编码方法，结合问题特点设计了新的抗体相似性定义方法及抗体抑制策略，并结合BRP周期性调度特点引入二次应答求解机制。运用标准算例测试表明：（1）一次应答测试中，本文算法在求解规模小于50个点的问题中，均能找到最优解，求解质量与分枝定界法相当，但速度更快；（2）在求解规模为50个点到100个点间的算例上，算法求解质量相较于GA提高1.02%；（3）二次应答测试中，二次应答的求解质量比一次应答的略高，但CPU消耗比一次应答快39%以上。

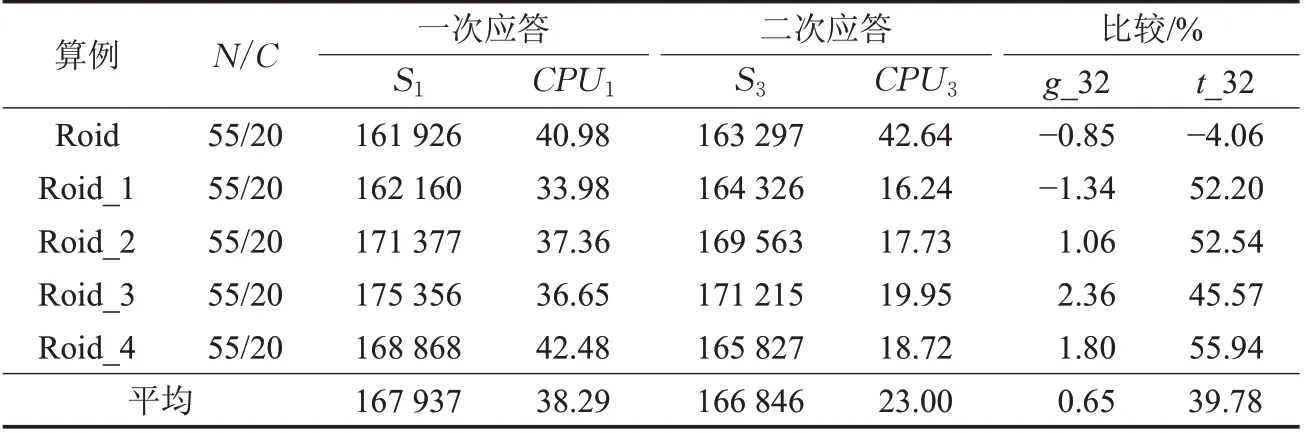
表4 二次应答测试(p=1)

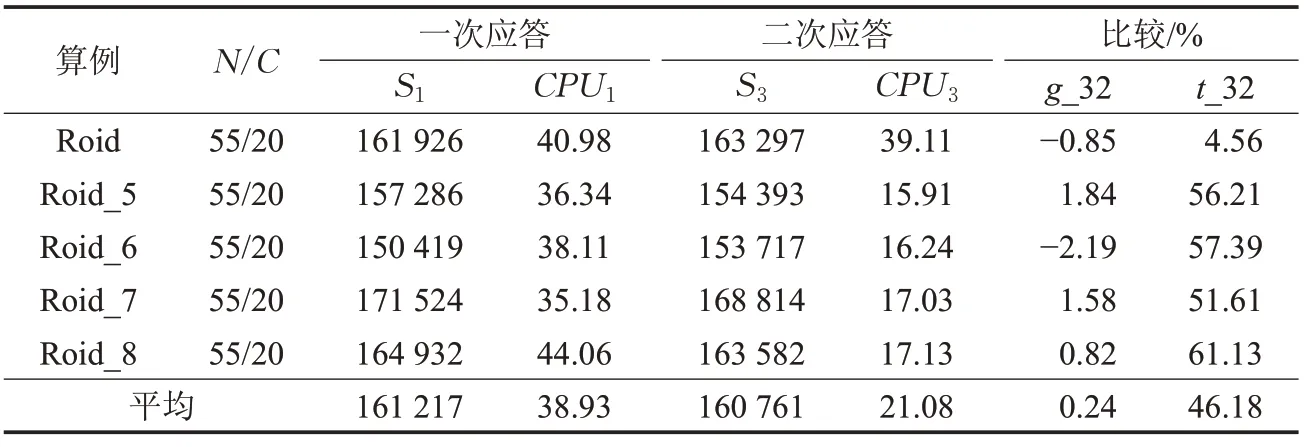
表5 二次应答测试(p=2)

表6 二次应答测试(p=3)

结合本文算法一次应答、二次应答的求解测试结果，本文认为，求解BRP的人工免疫克隆选择算法的求解速度较精确算法更有优势，求解质量与遗传算法相差不大，其二次应答机制能加快周期性问题的求解速度，在实现公共自行车再平衡实时调度方面能体现更好的实用性。公共自行车再平衡是一项系统工程，即与停靠点的规划布置有关，也与用户取用车习惯有关，还与运营平台再平衡调度管理策略有关，将这些因素融入BRP模型，设计新的问题类型与对应求解方法将是后续BRP问题的重要研究方向之一。