基于博弈论可变集模型的节水型社会建设评价

王 文 川，李 磊，徐 冬 梅

(华北水利水电大学 水利学院，河南 郑州 450046)

随着社会经济的快速发展，我国水资源问题日益突出，习近平总书记提出“节水优先、空间均衡、系统治理、两手发力”的新时期治水思路，因此建设节水型社会具有重要的意义。根据节水型社会建设情况要求，制定相应的水资源管理政策，能够为水资源合理开发利用、水资源配置等工作做出重要指示。节水型社会建设评价是节水型社会建设的基础环节，能够对区域节水建设情况进行定位，评价结果可为水资源的管理和有效利用提供支撑。

在节水型社会评价理论与方法方面，国内已有学者做出了一些研究成果。陈莹等人构建了一个关于节水型社会的层次架构，并使用层次分析法计算指标权重，通过将各个指标在一段时期内的发展变化并与国外的指标作横向比较进而确定不同指标的标准值[1]。褚俊英等人对我国节水型社会建设的问题上以及未来的发展方向进行了探讨[2]。张熠根据目前的水资源开发利用状况，对节水型社会建设评价指标体系进行了讨论，指出需要从水资源、生态建设、经济社会子系统3个方面来构建整个体系[3]。杨丽美等人在综合国内外有关文献的基础上，对节水型社会评价的研究从指标体系的建立、评价方法的选择和权重问题的确定进行了总结和概括，指出对于依然存在着大量随机和模糊信息的节水型社会评价系统，研究还应该进一步深入[4]。何俊仕等人参照已有的指标体系，根据归一化权重，采用物元分析法对辽宁省节水型社会建设做出评价[5]。黄乾等人使用熵权法确定权重，并利用模糊物元模型对山东省节水型社会建设情况进行评价[6]。栾慕等人采用层次分析法对江阴市的节水型社会建设情况进行评价[7]。杨瑞祥等人在分析长沙市的节水现状后，运用改进的逻辑框架法与层次分析法对其进行节水型社会建设情况进行评价[8]。

在赋权方法上，大多数学者只运用单一的赋权方法，而无论是主观赋权还是客观赋权，都具有局限性。本文运用的博弈论组合赋权方式，既考虑了决策者对属性的偏好，又消除了主观赋权法带来的主观随意性。在评价模型上，节水型社会的建设程度是一种模糊的概念，而节水型社会评价的各个指标通常是清晰的，根据这一特点，陈守煜教授提出的可变集的对立统一理论[7,9-12]能够很好地解决此问题。因此，本文提出利用可变集模型，采用博弈论组合主观与客观权重，以洛阳市为例，对其节水型社会建设情况进行评价，并与模糊综合评价法、模糊物元法、TOPSIS法和VIKOR法的结果进行比较分析，以期为其他城市开展此类工作提供借鉴。

1 基于可变集节水型社会评价的原理与方法

1.1 理论基础——对立统一定理

(1)

则在连续统上必存在

(2)

的渐变式质变点，如图1所示。

图1 对立统一定理示意

1.2 评价原理

对于节水型社会评价，可以看作一个可变模糊清晰混合集，即可变集。根据1.1节相关的对立统一定理，提出可变集节水型社会评价的原理。

设由n个节水型社会评价年份组成的集合U，uj为某一年的节水型社会评价年份，uj∈U,j=1,2,…,n。以指标i的特征值xij来衡量节水型社会的建设程度。按已知的m个指标c个级别标准值矩阵。

(3)

(1)设1类(h=1)为起步阶段。若指标i特征值xij相较于2类标准值区间的上界值ai2大，则特征值xij对1类的相对隶属度就为1，对其对立类2类的相对隶属度为0，则

(4)

(2)设c类(h=c)为建成阶段，若指标i特征值xij相较于(c-1)类标准值区间的下界值bi(c-1)小，则特征值xij对c类的相对隶属度为1，对其对立类(c-1)类的相对隶属度为0，则

(5)

(3)若h为2至(c-1)的中间类，标准值区间为[aihbih]，落在区间[gihgi(h+1)]的指标i特征值xij可根据以下准则对类别h，h+1的相对隶属度进行计算。

(6)

(7)

其中指标i对h，(h+1)类相对隶属度等于1的点分别用gih,gi(h+1)表示。根据其相应的物理概念，该值即为h，(h+1)级标准区间的中值，即

(8)

指标i的相对隶属度在小于h级，大于h+1级的范围内均应等于0，即

(9)

应用公式(4)～(9)可计算出对象uj指标i对级别h的相对隶属度矩阵

(10)

设指标i的权向量为

(11)

节水型社会评价是多指标的综合判断问题。通过对立统一定理，推导出综合相对隶属度模型。评价指标uj的指标特征值xij对级别h的综合相对隶属度模型可用公式(12)计算。

(12)

式中,α为优化准则参数，α=1为最小一乘方准则，α=2为最小二乘方准则，p为距离参数，p=1为海明距离，p=2为欧氏距离。当参数α=1、p=1时，公式(12)即为线性模型

(13)

根据综合相对隶属度模型公式计算得出节水型社会的评价年份uj对各个级别的综合相对隶属度向量

(14)

应用文献[12]中的类别特征值公式

(15)

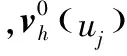
(16)

公式(16)的优点是增加了h，(h+1)间的中介类，能够使得评价分级更为细化，对节水型社会的定位有进一步的认识。

1.3 各指标组合权重的确定

本文利用博弈论组合赋权的方法对节水型社会指标进行权重计算。博弈论组合赋权的主要思想是以纳什均衡作为协调目标，在主观和客观赋权方法之间存在的冲突中找到一致和妥协[13]。这种综合主观和客观权重的方法，既能包含决策者对于指标重要性的排序，又能够体现出数据指标之间的内在规律。相较于单一形式的赋权法，更加全面、准确。

主观赋权法选用模糊层次分析法[14]，将模糊一致矩阵与层次分析法结合，相较于传统层次分析法，既保留层次分析法本身的优点，又克服了层次分析法中判断矩阵具有模糊性的缺点，保证了判断矩阵的一致性，更符合人类进行决策时的思想，计算步骤如文献[15]所示。

客观赋权法选用CRITIC赋权法，基本原理为：① 用标准差的形式表现同一指标在各个级别值间的差距大小，引入对比强度；② 若两指标间具有较强的正相关性，则两指标间冲突较低，反之较高[16]。该方法的优点为能够同时体现出指标间的变异性与关联性。计算步骤如文献[16]所示。

2 实例应用与结果分析

2.1 实例应用

本文以洛阳市节水型社会建设情况进行评价。引用《洛阳市节水型社会建设规划》[17]中洛阳市2007，2011，2015年以及2020年(近期目标)的相关数据，共9项指标，其各项值如表1所示。借鉴文献[18]中的对于节水型社会的评价标准，共分为5级：起步、初级、中级、高级、建成。标准值如表2所示。

表1 洛阳市节水型社会各年份评价指标值

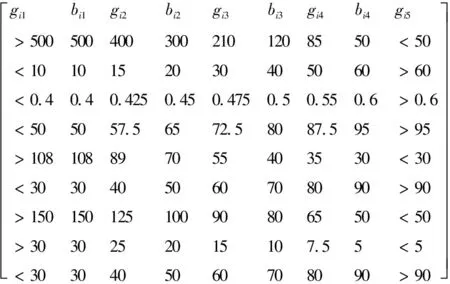
表2 节水型社会各评价指标标准值

根据可变集节水型社会评价原理，建立9个指标5个级别的标准值矩阵

根据矩阵Z与公式(8)计算得出相对隶属度为1的点映射矩阵G

将标准值矩阵Z中指标i相对隶属度为0.5的渐变式质变点插入矩阵G，得到指标i相对隶属度为1，0.5的点映射矩阵R

用2007年的指标数据为例对计算进行说明。已知2007年洛阳市单位GDP用水量为73 m3/万元，即特征值x11=73落入区间[gi4bi4]，根据公式(6)与公式(9)进行计算得到2007年洛阳市单位GDP用水量对各级的相对隶属度向量为

μ1(u1)=(0 0 0 0.829 0.171)

相应地计算2007年剩余8项指标对各级的相对隶属度向量，可以得到2007年洛阳市各级指标相对隶属度矩阵为

各个指标的权重结果如表3所示。

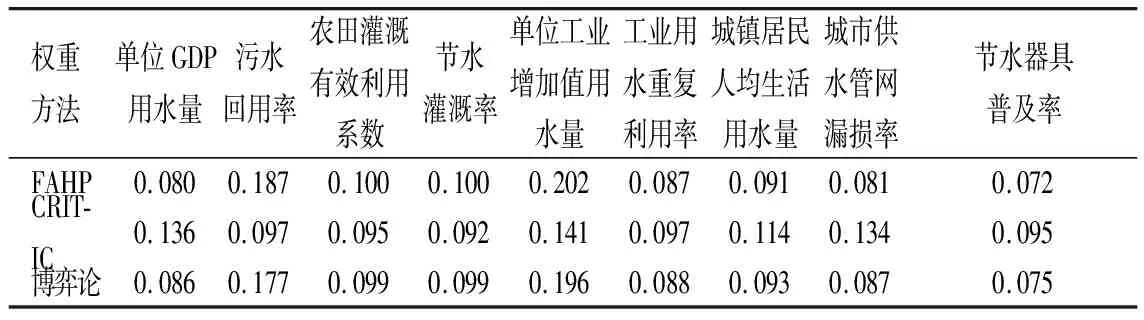
表3 节水型社会评价指标权重

令α=1，p=1，应用公式(12)得到2007年对各级的归一化相对隶属度向量为

v0(u1)=(0.164 0.337 0.292 0.191 0.016)

根据公式(14)，可以得到2007年洛阳市的级别特征值

H(u1)=2.556

同理，可分别计算2011，2015，2020年以及不同参数α=1、p=2，α=2、p=1，α=2、p=2的情况。

根据公式(16)计算评价等级:

其最终结果如表4所示。

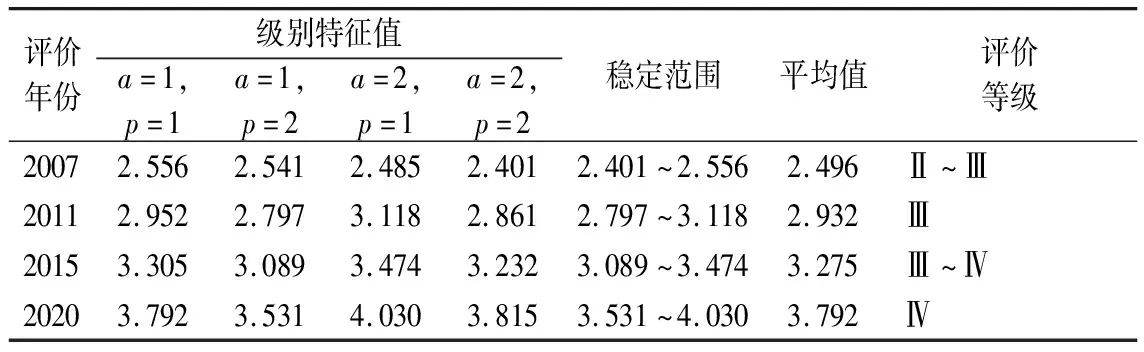
表4 各年份节水型社会评价结果

2.2 结果分析

为了更好地验证可变集模型对于节水社会建设评价的适用性，采用同样的赋权方式，运用模糊综合评价法、模糊物元评价法、TOPSIS法和VIKOR法对洛阳市节水型社会建设情况进行计算，结果如表5所示。

表5 可变集与多种模型评价结果对比

从表5中可以看出:2007年用可变集模型评价洛阳市节水型社会情况处于初级至中级之间，模糊综合评价法给出评价结果为初级，模糊物元法、TOPSIS法和VIKOR法给出的结果均为中级；2011年，所有评价结果均为中级；2015年可变集模型评价结果为中级至高级之间，模糊综合评价法的结果为中级，模糊物元法、TOPSIS法和VIKOR法给出的结果均为高级；2020年可变集与其他评价方法一致，洛阳市节水型社会建设水平达到高级。

对结果进行比较发现，2007年与2015年模糊综合评价法与模糊物元法、TOPSIS法和VIKOR法给出的结果不同，但是模糊综合法的缺点是分级不可避免地会缺失信息，而可变集模型地评价结果介于两者之间，说明其评价结果合理。本文采用基于博弈论的可变集模型对洛阳市的节水型建设情况进行评价，通过变化的模型及指标权重，分析确定稳定值的范围，其评价结果是稳定可信的。

3 结 语

本文利用博弈论组合模糊层次分析法与CRITIC赋权法的权重，利用可变集模型对洛阳市节水型社会进行评价。主要结论如下：

(1)运用主客观赋权法相结合的方法进行赋权，能更好地将数据内部的内在规律与决策者对于评价对象不同程度的重要性相结合，得出的最终权重具有一定的代表性。

(2)从计算结果可以看出，洛阳市2007年节水型社会建设程度处于初级至中级之间，2011年达到中级阶段，2015年能够达到中级至高级之间，2020年就可以达到高级阶段。洛阳市节水型社会建设情况呈现一种发展向上的趋势，节水情况会越来越好。

(3)本文利用模糊综合评价法、模糊物元法、TOPSIS法和VIKOR法与计算结果进行对比，结果表明，可变集评价结果更加准确、合理。