基于索引-存根表的云存储数据完整性审计

赵海春，姚宣霞，郑雪峰

1) 内蒙古民族大学计算机科学与技术学院，通辽 028000 2) 北京科技大学计算机与通信工程学院，北京 100083

由于云计算有诸多优势，许多个人和组织选择将其数据和业务流程转移到云存储中，以减轻本地存储的负担并降低相应的维护成本[1−2]. 然而，与传统的系统相比，用户对存储在云中的数据失去了直接的物理控制. 因此，尽管云计算基础设施比个人计算设备更加强大和可靠，但由于云计算存在着各种内部和外部的威胁，数据安全和隐私保护问题仍然是用户采用云服务的核心考虑因素[3].

由于云存储服务器（Cloud storge server, CSS）可能是不完全可信的，因此，用户需要定期检查其存储在云中的数据是否完好无损. 由于用户一般只有有限的计算、存储空间和网络带宽等资源，因此，可以将数据完整性验证的任务委托给一个专业的第三方审计者（Third party auditor，TPA）来完成[4−6]. 然而，这将导致用户数据及相关信息在审计过程中会泄漏给TPA，由此引出了隐私保护的问题. 近年来，研究人员基于同态认证码、随机掩码和数据块随机抽样等技术，提出了隐私保护的云存储公共审计方案，以实现远程检查外包数据的完整性[5, 7−8]. 其中，一些方案中，由于在数据块签名的构造中包含了与块索引i相关的信息，例如，如果该哈希值出现重复，可能会遭受数据块签名的伪造攻击[10]. 因此，使得设计和维护相关的索引表变得繁琐. 针对这个问题，本文中提出了一个结构简单且易于维护的索引-存根表（Index-stub table,IST）结构，并基于该结构提出了一个隐私保护的云存储公共审计方案. 该方案能够有效地支持远程数据的动态更新及在审计过程中数据的隐私保护性，其中的数据块签名构造中，未涉及块索引相关的信息. 文中基于CPoR证明框架[11]和相关的归约证明方法[12]，针对方案所提供的数据的完整性保证及其在审计过程中数据的隐私保护属性分别给出了形式化的安全证明.

1 相关工作

2007年，Ateniese等[13]基于同态可验证标记（Homomorphic verifiable tags，HVTs），提出了“可证明数据拥有”（PDP）模型，并在该模型下，提出了两个PDP方案，方案中通过从服务器端随机抽取数据块来生成对数据拥有的概率证明. 该方案被认为是第一个同时提供无块验证和公共验证的方案. Juels和Kaliski[14]提出了一个“可取回性证明”（PoR）模型，并提出了一个PoR方案，通过使用抽样检查和纠错码等技术，确保了对外包数据的可拥有性和可取回性. 但是，用户能够执行的验证次数是预先确定的，而且方案未能支持公共可审计性. 在此基础上，Shacham等[11]设计了一个CPoR（Compact PoR）模型，并在Juels-Kaliski模型中给出了CPoR模型能够抵御任意敌手的安全性证明. 文中基于BLS签名技术提出了一个公共可验证的CPoR方案. 2009年，Erway等[15]基于跳跃表结构，提出了支持动态数据操作的PDP（Dynamic PDP，DPDP）. 该方案利用跳跃表结构来确保数据块签名的完整性，并通过数据块签名的完整性来保证数据块的完整性. 该方案能够有效地支持外包数据的动态操作. 2011年，Wang等[16]提出了一个能够同时支持动态数据操作和公共可审计的方案，方案中的认证信息是通过Merkle哈希树（MHT）进行管理的，树中叶节点的数据项值为H(mi). 然而，Liu等在文献[6]中指出，由于该方案中的MHT没有包含块索引信息，所以，该结构不能够验证数据块的索引值，由此可能会导致替换攻击. 同时，Liu等提出了一个基于自上而下的多副本MHT的云存储大数据公共审计方案，该方案支持动态数据更新. 2013年，通过利用随机掩码技术对响应信息进行盲化处理，Wang等[5]又提出了隐私保护的公共审计方案. 然而，文中对动态数据操作部分没有给出清晰的描述. Yu等在文献[7]中提出了一个基于身份的支持完美数据隐私保护的远程云存储审计方案. Mo等在文献[8]中提出了一个云存储中不可否认的数据拥有验证方案，该方案不仅可以让用户检测到云服务器是否丢失了用户的数据，还可以保护云服务器不被恶意用户敲诈. 2015年，基于多项式剩余定理，Yuan和Yu[17]提出了一种公共可验证的云存储PoR方案，该方案中用户端的通信量和计算开销均为常量. 在此方案的基础上，Zhang等[18]提出了一个改进的安全模糊审计协议. 研究人员还提出了其他一些远程数据完整性检查的方案[19−24]，这些方案分别对远程数据完整性检查的不同方面进行了研究.

2 问题陈述

2.1 系统模型

本文中研究的云存储数据审计系统包括：云用户、CSS和TPA等三个实体，如图1所示.

图 1 包含CSS、云用户和TPA的云存储架构Fig.1 Cloud storage architecture with CSS, cloud users, and TPA

云用户是数据所有者，他们有大量数据文件需要存储在CSS中，并且可以通过与CSS交互来访问和动态更新他们的数据. 由云服务提供商（CSP）管理的CSS具有大量的存储、计算和网络带宽等资源. 存储在云中的用户数据由CSP管理和维护. TPA具有大多数用户所不具备的专业技术和能力，并且可以在用户的委托下代表用户对外包数据进行完整性审计.

为确保外包数据的完整性和正确性，用户需定期进行检查. 为了节省计算资源和网络带宽等，用户可以将此任务委托给TPA. 然而，在审计过程中他们一般不希望数据内容被泄露给TPA.

在这个模型中，本文假设云服务器没有动机向任何外部实体透漏其所托管的数据. 同时，还假设TPA没有动机在审计过程中与CSP或用户串通，然而，TPA对用户的数据内容是感兴趣的.

2.2 设计目标

在此模型下，文中提出了一个云存储公共审计方案，该方案预期达到的设计目标如下.

（1）公共可审计性：在用户的委托下，允许第三方审计者（TPA）在不下载整个文件副本的情况下，验证外包数据的完整性.

（2）存储正确性：确保不存在能够在没有完好地存储云用户数据的情况下通过TPA审计的CSP.

（3）隐私保护：确保TPA不能从审计过程中收集的信息获取用户的数据内容.

（4）高性能：TPA能以较小的通信量和计算开销完成对外包数据的完整性审计.

（5）支持数据动态操作：允许数据所有者随时对云存储中的数据进行修改、插入和删除数据块等更新操作.

3 基于索引-存根表的云存储审计方案

3.1 索引-存根表

索引-存根表（Index-stub table, IST）是一个二维表，表中只有两个数据项：数据块的序号和数据块的存根值，如表1所示. 每个数据块对应的存根值为(H(mi))α/β，该值是数据块认证符（或签名）构造中的一个组成部分，其中，mi为第i个数据块，α和β为用户的密钥. 用户端保留存根，而将数据块的认证符作为票据发送给服务器，如图2所示.

表 1 索引-存根表Table 1 Index-stub table

图 2 存根与票据Fig.2 Stub and ticket

如果没有密钥，任何人伪造出有效的存根都是困难的. 通过IST表，用户可以有效地监视服务器端的行为. 存根值可以用于检查数据块认证符是否完整，进而通过认证符的完整性来验证数据块的完整性. 同时，能够保证数据块的顺序不会被改变. 相比于MVT表[9]和IHT表[4]，IST表结构更简单、更易于维护，而且无需考虑块索引值重复而引发的伪造攻击.

将数据文件上传到服务器之后，IST表保存在用户端. 当用户对数据文件进行数据块修改、插入和删除等操作时，IST表也要进行相应地更新.当用户委托第三方审计者对数据进行完整性审计时，还要给TPA发送一个IST表的副本，此后，只有数据进行了更新操作，才会再次发送副本.

3.2 方案描述

本文遵循了文献[16, 25−27]中使用的概念，在CPoR模型[11]和文献[28]中的相关方法的基础上，基于索引-存根表结构，提出了一个隐私保护的云存储审计的方案.

该方案包括两个算法KeyGen(1k)，St(sk,F)和一个交互式审计协议Audit(CSP,TPA)[29−30].

设S=(p,G,GT,e)为一个双线性映射群系统，随机选取两个生成元g,h∈RG，其中，G,GT是两个阶为大素数p的群. 函数H(·)是一个安全的密码学哈希函数，即H:{0,1}∗→G，它将字符串均匀地映射到G中. 另一个散列函数h(·)，将GT中的群元素均匀地映射到Zp，即，h:GT→Zp.

St(sk,F)：将文件F切分成n×s个区，mij∈Zp. 云用户选择s个随机值τ1,···τs∈Zp作为文件的秘密值，并计算uj=gτj∈G,1≤j≤s和每个数据块i的认证符：

用户从Zp中均匀随机地选取fn作为文件F的标识符. 设t0为“fn||n||u1||···||us”，云用户计算SSigssk(t0)，并将t=t0||SSigssk(t0)作为F在私钥ssk下的文件标记. 然后，用户将F连同认证符集合Φ=(σ1,···,σn)上传到服务器，上传完成后，这些数据可以从本地存储器中删除. 用于检查外包数据完整性的IST表，需要保存在用户的本地存储器中，在对文件进行各种更新操作时，由用户来维护.

当用户委托一个TPA来完成数据完整性检查时，被授权的TPA首先提取文件标记t，利用spk检查t中签名的有效性，如果验证失败，则发出“错误”并退出；否则，TPA恢复出fn. 然后，可以定期启动下面的审计协议.

Audit(CSP,TPA): 它是一个在CSP和TPA之间的三步（3-move）协议，运行过程描述如下所示.

（1）承诺阶段（CSP→TPA）：CSP选择s个随机值λj∈RZp， (1≤j≤s)，然后计算Tj=ujλj，(1≤j≤s)，并将值：{Tj}1≤j≤s，作为承诺信息发送给TPA.

（2）挑战阶段（CSP←TPA）：收到承诺信息后，TPA随机选择一组挑战信息Chal={c,k1,k2}，其中，c是要验证的数据块的个数，k1,k2分别是伪随机置换πk和伪随机函数fk的随机密钥. πk和fk分别用于生成被挑战的c个数据块的索引值sx(1≤x≤c,1≤sx≤n)和对应的线性运算系数vi(i∈{sx|1≤x≤c},vi∈RZp). 现假设用I表示c个随机索引值的集合{sx}1≤x≤c， 用Q表示被挑战块的索引值与其系数构成的对集合{(i,vi)}i∈I. 接下来，TPA将挑战信息Chal发送给证明者CSP.

（3）应答阶段（CSP→TPA）：在接收到Chal后，CSP随机选择r∈Zp，并计算sx=πk1(x)，vi=fk2(x)，ψ=e(gr,h)，γ=h(ψ)，σ和µ，其中，

然后，证明者CSP将响应值θ=(σ,µ,ψ)发送给验证者TPA.

验证：TPA计算γ=h(ψ)，然后，验证下面的等式是否成立，如果成立，输出“接受”，否则，输出“拒绝”.

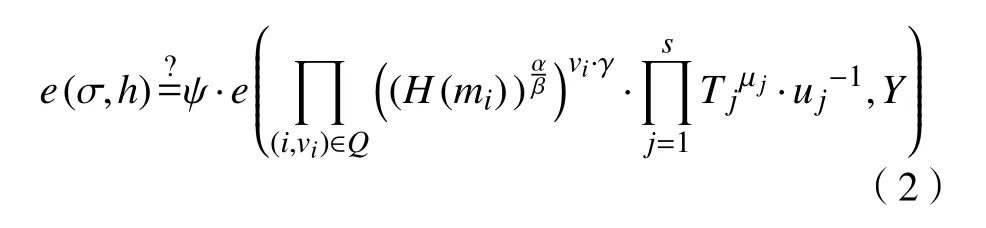
对于每一个随机挑战Q及其正确的响应值，方程的正确性可阐述如下：

等式的右边=

等式的左边

因此，这意味着方程对于正确的应答信息是有效的.

3.3 支持批量审计

当TPA同时处理D个不同用户分别对D个不同文件进行审计的委托时，为了更高效地完成审计任务，通过扩展该方案使其具有批量审计功能. 如果集合Q中的i值在被审计文件的文件块数量范围之内，则可以将该文件的审计任务添加到批审计中，以实现对多个审计任务的一次性执行.批量审计相对于分别单独审计来说，可以将计算消耗稍大的双线性对操作（Pairing operation, PO）的数量从2D减少到D+1.

假设第k个用户选择的参数为uk,j∈RG, 1≤k≤D,用户的外包文件为文件名为fnk，文件标记为文件中第i个数据块的签名是:

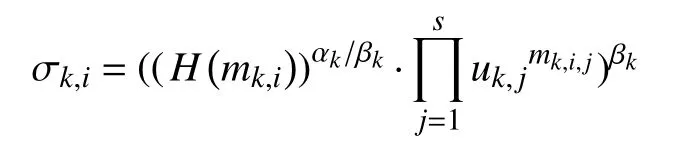
CSP选择的参数为λk,j∈RZp，然后计算Tk,j=uk,jλk,j并将其作为用户k的承诺. TPA选择挑战值为Chal={c,k1,k2}，并将其发送到CSP. 接收到Chal后，CSP计算出Q={(i,vi)}i∈I，随机选择rk∈RZp，然后，计算ψk=e(grk,h)和

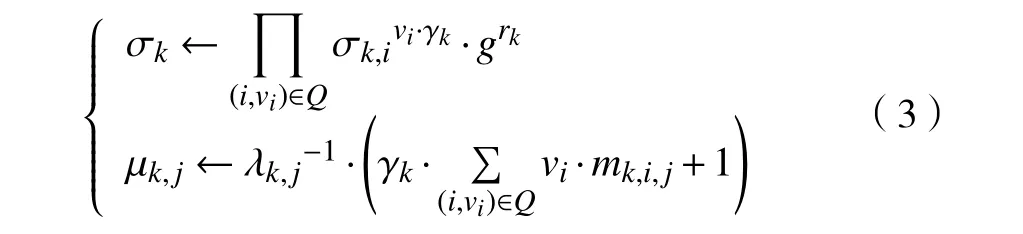
在接收到CSP的响应信息后，TPA检查下面的等式是否成立，如果成立，输出“接受”，否则，输出“拒绝”.

3.4 支持数据动态操作

该方案能够对外包数据进行各种数据块级的动态操作，包括：修改（‘M’）、插入（‘I’）和删除（‘D’）数据块等操作，这几种动态操作的过程描述如下.

3.4.1 修改操作

对于一个文件F={m1,m2,···,mn}，假设用户想要将某个数据块mi修改为数据块，用户执行PrepareUpdate(·)算法以完成以下操作.

在收到用户的修改操作请求后，CSS执行PerformUpdate(·)算法以完成以下操作.

（1）将数据块mi替换为，获得文件F的一个新版本；

（2）将集合Φ中的σi替换为.

3.4.2 插入操作

对于文件F={m1,m2,···,mn}，假设用户想要在第i个数据块后面的位置插入一个新的数据块用户执行PrepareUpdate(·)算法来完成以下操作.

在收到用户的插入操作请求后，CSS执行PerformUpdate(·)算法来完成以下操作.

（1）在文件F中第i块后面的位置插入数据块mi+1′，从而获得文件F的一个新版本；

（2）将σi+1′插入到集合Φ中第i个位置后面.

3.4.3 删除操作

如果用户想要删除文件F中第i个数据块，首先，从IST表中删除第i条记录，并向CSS发送删除操作请求“update =(fn,D,i,mi,σi)”.

在收到用户的这个请求后，CSS运行PerformUpdate(·)算法来执行以下操作.

（1）删除数据块mi，获得文件的一个新版本；

（2）从集合Φ中删除σi.

4 安全分析

4.1 可靠性（Soundness）分析

可靠性意味着证明者错误的响应值被验证者接受为正确的响应值的可能性很小. 在此上下文中，这意味着如果用户的外包数据没有被完好地保存时，那么CSS将无法对TPA的挑战生成有效的响应，如定理1中所述. 我们的安全性证明依赖于计算Diffie-Hellman问题和离散对数问题在双线性群中是困难的假设.

定理1 如果CSS能够通过Audit(·)协议的数据完整性审计验证过程，那么，它确实完好无损地存储着指定的数据.

基于CPoR中的证明方法（文献[11]中定理4.2），我们在随机预言机模型中给出了定理1的证明.

现存在一个挑战者和一个敌手A（即，恶意的CSP）. 挑战者构造了一个模拟器S，它将为敌手A模拟出该方案的整个环境. 对于之前进行过St问询的任何文件F，敌手A都可以与挑战者一起执行Audit(·)的审计协议. 在这些协议执行过程中，模拟器S扮演验证者的角色，而敌手A扮演证明者的角色：S(pk,sk,t)⇌A.

对于某个文件F，如果敌手A能够以不可忽略的概率成功地伪造聚合签名σ′，导致，且能够通过数据完整性审计验证，那么，模拟器可以利用敌手A解决计算Diffie-Hellman困难问题.假设该模拟器的输入值为h,X=hα,Y=hβ，其目标是输出hα·β.

设H:{0,1}∗→G为一个哈希函数，将被建模为一个随机预言机. 模拟器将对随机预言机H进行编程. 当回答敌手A的问询时，模拟器随机选择， 并用hr∈G作为响应值，当回答形如H(mi)的问询时，模拟器以下面描述的特殊方式对预言机进行编程.

对于每个j, 1≤j≤s，模拟器选择随机值并设置uj←(X)ηj·hθj..

对于每个i, 1≤i≤n，模拟器选择一个随机值并将i值处的随机预言机编程为

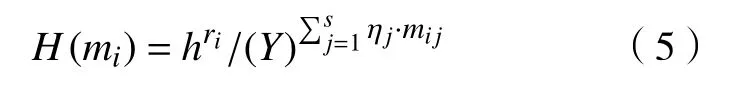
接下来，模拟器计算：

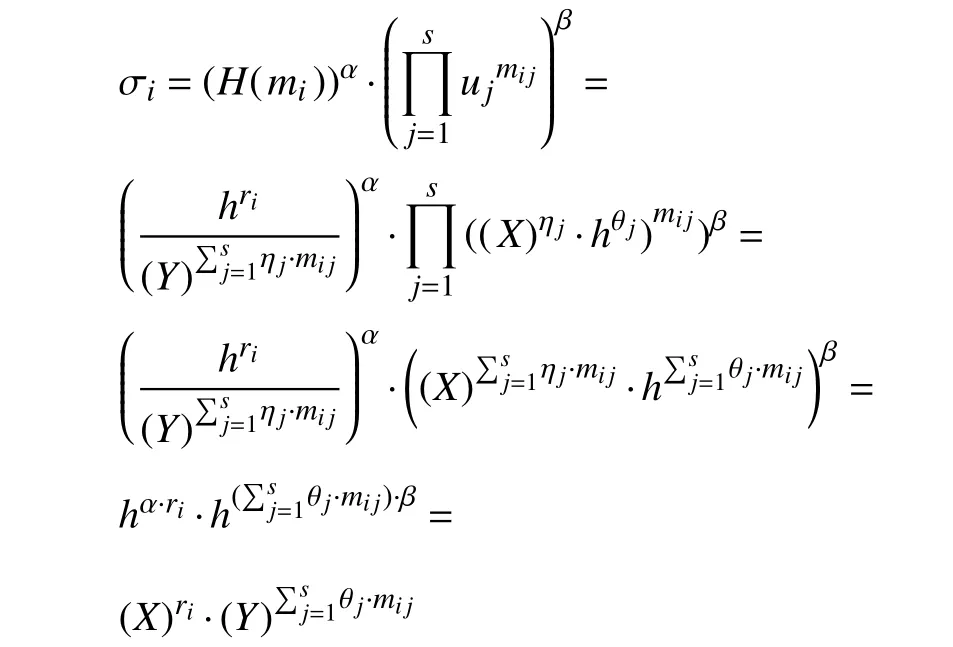
挑战者保存一份对敌手A提出的St问询的响应列表. 然后，挑战者观察与对手A执行的每一个Audit(·)审计协议的实例，如果在任何一个实例中，敌手是成功的（即，验证方程成立），但敌手的聚合签名，则挑战者宣告失败并中止.

假设挑战值Q={(i,vi)}是导致挑战者中止的问询，敌手对该问询的响应值是假设期望的响应值为µ1,µ2,···,µs和σ，通过方案的正确性，可知期望的响应值满足验证方程：

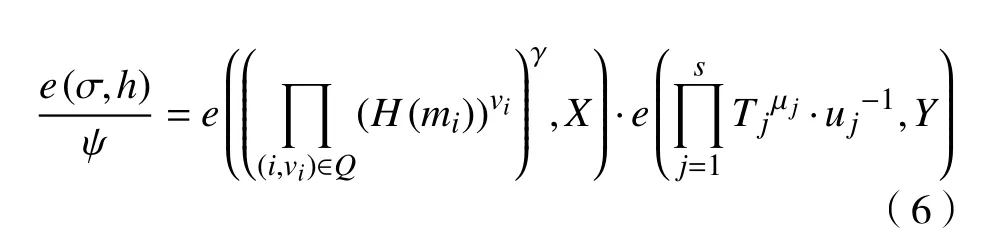
因为挑战者中止了，所以我们知道σ≠σ′并且σ′通过了验证方程：

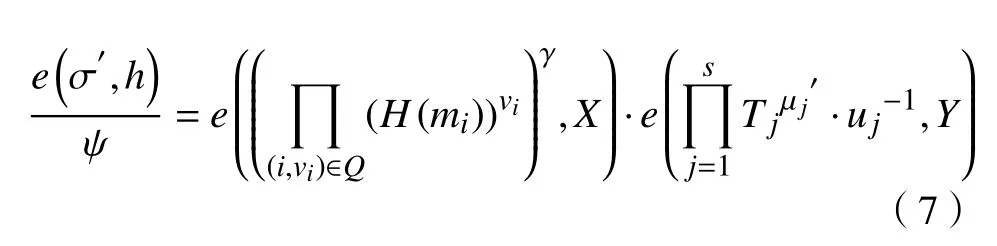
可以观察到，如果对于每个j，都有那么我们可以得到，这与我们上面的假设相矛盾. 因此，如果我们定义那么一定是集合{∆µj}中至少有一个值是非零的. 设用等式（7）除以等式（6），我们得到

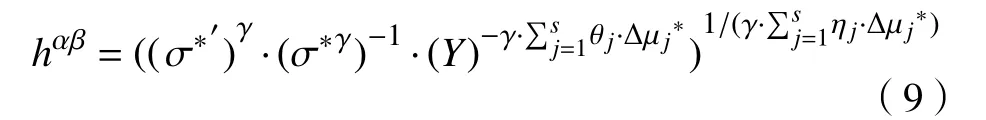
如前所述，我们知道σ′=σ. 由等式（6）和（7）可以得到：

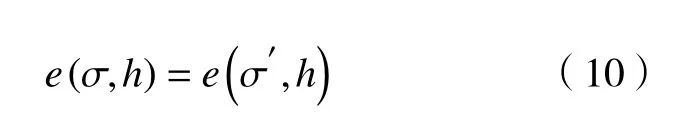
通过代入µ和µ′的值，我们得到

因此，我们发现了解决离散对数问题的方法，

4.2 隐私保护保证

隐私保护属性是确保TPA无法从审计过程中收集到的信息中提取用户数据.

定理2 TPA不能从CSP的响应信息θ和IST表中的中提取用户的数据内容.

证明：由于mi，α和β的值对TPA都是隐藏的，因此H(mi)的值不能通过确定. 虽然e(H(mi),X)等于的值也不能从中计算出来. 因为由得出的同构被认为是单向函数[31]，当给定时，计算出P是不可行的. 因此，要从中恢复mi是困难的. 同理，从σ中提取σi也是困难的.

每一个λj都是由CSP随机选择的，而是它的逆值是通过值进行了盲化处理，因此，在每次响应中的µj值都均匀地分布在Zp中. 虽然TPA可以得到足够多的数据块mi及其系数vi的线性组合，但如果想要获得µj∗的值，则必须首先得到λj−1. λj可由Tj=ujλj, (1≤j≤s)计算得到，然而，这意味着要解决离散对数问题（DLP）. 由于DLP的困难假设，TPA在多项式时间内计算出值是不可行的. 因此，从µj(1≤j≤s)中获得用户数据是困难的.元素，这两个值对TPA都是隐藏的.

5 性能评价

为了评价该方案的性能，我们分别进行了相关的理论分析和实验比较.

5.1 理论分析

理论分析的目的是从理论上将我们的方案与类似的方案在用户端、服务器端和审计者等三方的计算开销进行比较.

首先，为了便于描述，在表2中指定了一些基本的运算操作符号[32]. 接下来，对新提出的方案与文献[5]中提出的方案在计算开销方面进行了相应的比较和分析，如表3所示.

表 2 符号和相关操作说明Table 2 Notations of relevant operations

用户端的主要运算操作是计算文件中数据块的签名、文件的标记和一些公共参数. 将这些计算开销合并在一起，即可得到用户端的计算总开销. 从表3中可以得出，在用户端的计算开销上，新提出的方案比文献[5]中的方案多了，而对方相比于我们的方案多了所以，在用户端的效率上，我们的方案要略优于文献[5]中方案.

服务器端的计算开销包括生成审计阶段的承诺信息和响应信息两个方面. 从表3中可以看出，在服务器端，文献[5]中的方案比新提出的方案多出，由于有s−1次对操作（PO），这部分计算开销较大. 而相比于文献[5]中的方案，新提出的方案多出的计算开销为，然而，将其中的指数运算部分与对方多出的指数运算相互抵消后，新提出的方案多出的计算开销在总开销中占的比例很小，几乎是可以忽略不计的. 所以，新提出的方案在CSP端的计算开销要优于另一个方案. 而这两个方案在TPA端的计算开销基本相当. 因此，从理论分析可知，我们的方案是高效的.

5.2 实验比较

为了验证上述理论分析的结果，我们进行了相关的实验. 我们在0.5.14版本的Pairing-based cryptography（PBC）库上进行了实验，实验在Ubuntu Linux系统上用C语言编程实现. 硬件平台配备主频为3.60 GHz的Intel Core i7-4790 CPU、8 GB的DDR3内存和7200转/分的Seagate 1 TB驱动器.实验中使用的椭圆曲线是一条MNT曲线，基域大小为159位，嵌入度为6.p的位长度是160位. 测试数据是随机生成的100 MB的文件.c值的选择是基于文献[13]中的概率框架. 所有实验结果均为30次试验的平均值.

表 3 不同的隐私保护方案之间的计算开销比较Table 3 Comparison of the computation overhead of different privacy-preserving schemes

5.2.1c值的选择

图 3 概率框架的计算过程Fig.3 Computation process of the probabilistic framework

5.2.2 批审计的效率

为了验证批审计的效率是否真的优于分别单独审计的效率，在相同的实验环境下，对新提出的方案分别进行了批量审计和分别单独审计的相关实验测试. 在实验中，s取值为1，审计的任务数从10个增加到150个，每间隔10个做了一个实验，为了便于比较，将单独一个任务的情况也进行了实验. 最后，用每次实验中得到的总审计时间除以相应的任务数，得到了单个任务的平均审计时间，如图4中所示，批量审计的平均审计时间明显低于分别单独审计的平均审计时间，可以使TPA节省大约4%的时间.

5.2.3 方案之间的比较

图 4 批量审计与分别单独审计的平均审计时间比较Fig.4 Comparison of the average audit time between the batch audit and separate audit

为了验证新提出的方案在审计过程中的效率，针对方案中的TPA和CSP的计算开销，我们将该方案与文献[5]中提出的方案分别进行了实验比较，如图5和6所示. 从图5中可以看出，新提出的方案在TPA的计算开销方面，略优于另一个方案，但总体上两个方案之间差别微小，因为在值相同的两条曲线之间的距离很小，只有在c=460时，基于IST表的方案的曲线，随着s值的增加，斜率有减小趋势. 从图6可以看出，就CSP的计算开销而言，我们的方案在CSP端的计算开销明显优于文献[5]中提出的方案.

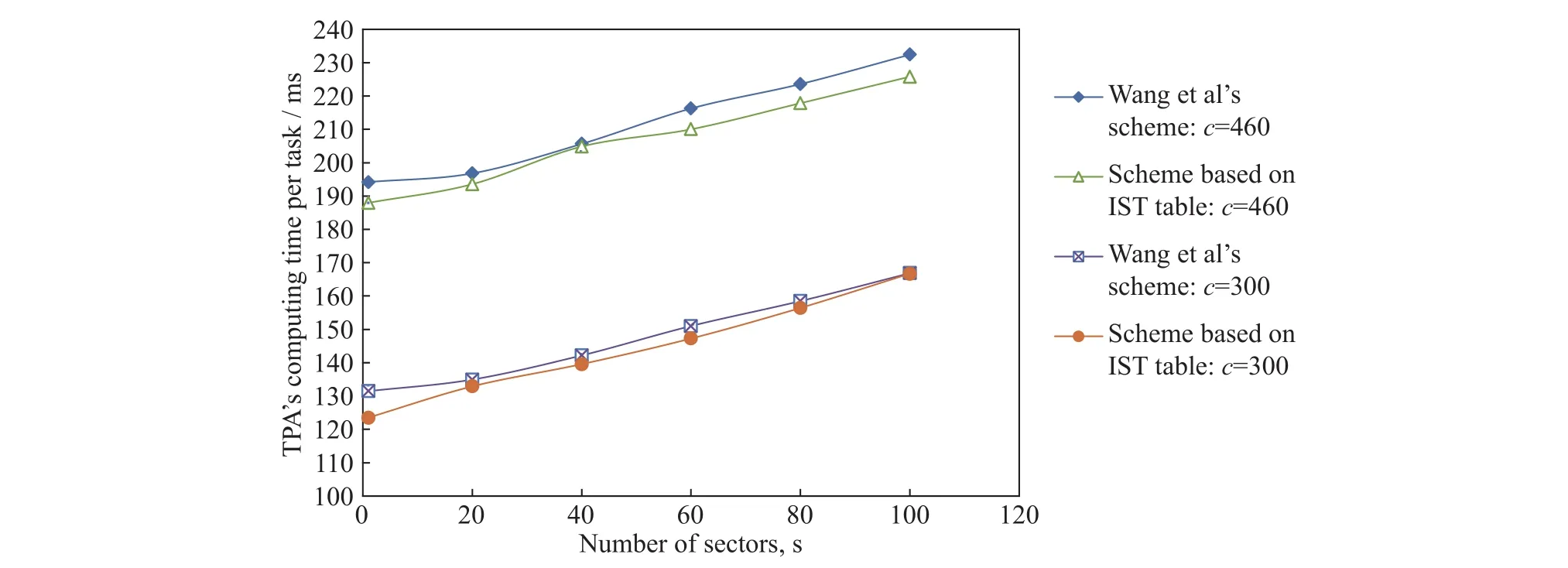
图 5 TPA的计算时间比较Fig.5 Comparisons of the TPA computing time

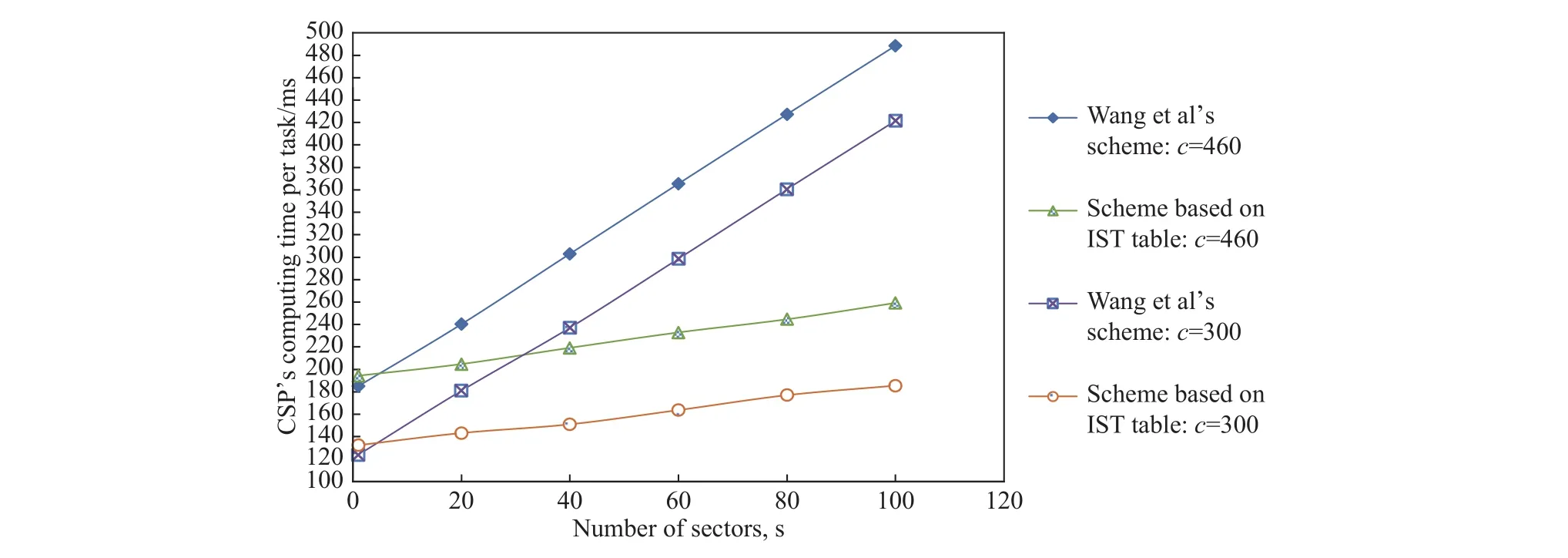
图 6 CSP的计算时间比较Fig.6 Comparisons of the CSP computing time

6 结论

本文中提出了一个索引-存根表的结构，并基于该结构提出了一个具有隐私保护属性的云存储第三方审计方案. 该方案能够支持各种数据块级的动态操作. 通过索引-存根表结构，可以有效地降低用户端的维护难度. 相关的安全分析表明，该方案是可证明安全的，并且在TPA审计阶段具有隐私保护的属性. 在性能分析部分，进行了相关的理论分析和实验比较，结果表明该方案是高效的.