灾后巷道堆积体力学特征分析

郭长恒，邢玉忠

（1.太原理工大学 安全与应急管理工程学院，山西 太原030024；2.山西省煤矿安全研究生教育创新中心，山西 太原030024）

随着开采深度的加深，地质灾害发生的频次与烈度显著增加[1-3]。如何有效开展灾后救援工作成为亟待解决的问题[4-6]。通常，为减少工程量、缩短救援时间，将沿原巷道到达待援人员驻留区作为第一救援路线。救援过程中，救援人员最怕遇到堆积体阻塞巷道中断救援路线的情况。对于灾后巷道堆积体的研究，文献[7]分析推导了垮空区高度计算公式以及巷道垮塌后造成堵塞的判定条件。文献[8]分析了复合顶板的垮塌状态,并根据不同的顶板条件，从灾后救援角度出发提出了救援工程建议。文献[9]分析了断层破碎带的地质特征和垮落堆积体特征，推导了冒空区高度、宽度与堆积范围计算公式。文献[10]针对救援通道位置和断面形状选择问题，通过数值模拟，给出了救援通道的优选位置及断面宜选形状。文献[11]阐述了灾区变坡巷道堵塞特征，构建了灾区变坡巷道物理模型和力学模型。文献[12]运用CDEM 软件，对回采巷道上覆岩层进行数值模拟，探讨了巷道垮塌堆积体内部块体之间的力学关系。由于断层破碎带具有稳定性差、继冒性强的特点，该地段最易导致巷道垮塌，该条件下打通救援通道尤为困难，且危险性高[13-15]。救援路线经过巷道垮落堆积体时，必然触及垮落堆积体边界作用力分布问题。上述专家虽然从救援通道位置、形状、堆积体内块体间的力学关系等角度进行了相关研究，但对于垮落堆积体边界作用力的问题均未涉及。据此，以断层破碎带灾后垮落堆积体堵塞救援线路为背景，针对堆积体边界作用力的分布规律开展理论研究，并进行实验验证，旨在为灾后应急救援通道开挖提供支持。

1 断层破碎带垮落堆积体特征分析

断层破碎带是由地质构造运动形成的，通常由断面之间的碎块充填区和派生裂隙区2 部分组成[16-18]。碎块充填区内块体无明显棱角，排列松散，胶结作用差。而派生裂隙区内块体棱角分明，排列次序与地层顺序一致[19-21]。

为分析断层破碎带垮落堆积体特征，现场勘查了某煤矿断层破碎带巷道段垮落堆积体堵塞巷道的情况，堆积体具有如下特征：

1）堆积体较为松散，胶结作用差，基本堵塞整个巷道，在巷道中分布不均。

2）堆积体碎块大小不一，但均无明显棱角。据此推测，断层破碎带巷道段的垮落主要以岩石碎块充填为主。

3）垮落后的岩石碎块，受自重力和岩石间冲击力作用，不断进行自身调整，不断达到新的平衡。由此可见，堆积体的形成是岩石碎块不断进行“自组织”调整的过程。

根据堆积体特征可初步推测，巷道两帮对堆积体仅起限制作用，堆积体边界作用力属于被动抗力，且源自于块体堆积过程中的滑移效应。

2 堆积体边界作用力理论分析

参照对堆积体边界作用力的推测，堆积体边界被动抗力分析如图1，选取图1（a）中最高点右侧ABCD 区域的堆积体进行力学分析。

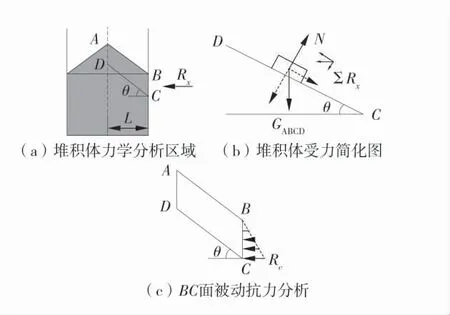
图1 堆积体边界被动抗力分析Fig.1 Analysis of passive resistance at accumulation body boundary

由受力分析可知，垂直于ABCD 平面单位长度堆积体的重力GABCD为：

式中：ρ 为堆积体的平均密度；hBC为C 点在堆积体中埋深，即BC；L 为堆积体最高点距边界的水平距离。

图2（b）为堆积体ABCD 部分受力简化图，由图可知，堆积体边界BC 面的总抗力∑Rx为堆积体沿DC 面自然堆积而被动产生，θ 角的形成也是由于堆积体自然滑落产生，因此，堆积体在DC 面上的摩擦力f 可视为0。因此，

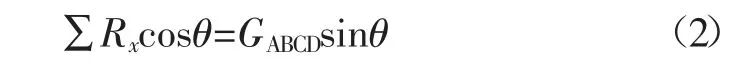
将式（1）、式（2）合并，整理可得：

由图2（c）可知，BC 面上的被动抗力呈三角形分布，因此，C 点的被动抗力可由式（4）表示：

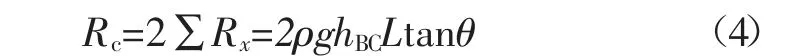
式（4）为堆积体边界被动抗力计算式，由此可知，断层破碎带垮落堆积体边界被动抗力是关于堆积体密度ρ、堆积体深度h、堆积体最高点距边界的水平距离L、自然安息角θ 的函数。

3 堆积体边界作用力测定实验

式（4）得出的前提是堆积体边界作用力源于碎块堆积过程中的滑移效应，该前提是否成立，以及作用力是否符合式（4），还需实验验证。

3.1 实验装置

根据堆积体堆积特点和研究内容需要，设计了堆积体边界被动抗力测定实验装置，实验装置图如图2。该装置分为5 部分：试验箱、传感器、数据线、数据采集仪、电脑。

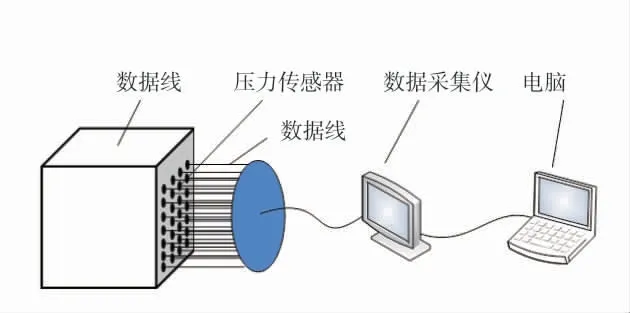
图2 实验装置图Fig.2 Diagram of experimental equipment

试验箱材料为：前侧(正面侧)为高强钢化玻璃，其余面为木板。箱体高h 为1.1 m，左右宽度w1为0.8 m，前后宽度w2为0.4 m。传感器布置在侧面，传感器布置和凹槽型装置如图3，传感器布置7 排，每排布置4 个，共计28 个传感器。传感器间排距为0.1 m。为辨识每个传感器的位置，分别对传感器以x-y 形式编号，其中x 表示第x 排，y 表示第y 列，如：3-2 传感器表示位于第3 排、第2 列的传感器。为保证碎块放入实验箱在传感器侧前后形成的堆积体高度相等，设计了宽度可调的凹槽型碎块装入装置（图3（b）)。实验过程中，凹槽型碎块装入装置放置于箱体顶部。

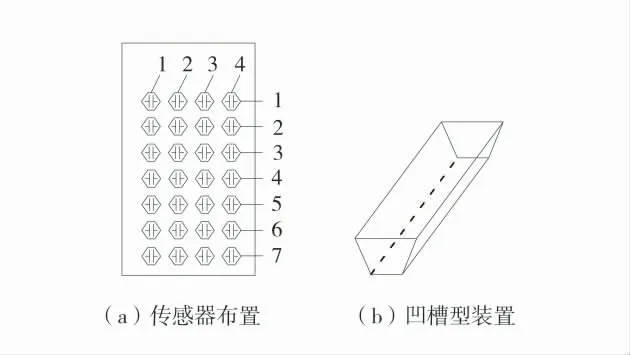
图3 传感器布置和凹槽型装置Fig.3 Sensor arrangement and groove type device

3.2 实验过程

制定的实验方案见表1。

表1 实验方案Table 1 Experimental scheme

为了测定堆积体边界作用力分布情况，试验步骤如下：

1）调试与清零处理。连接实验装置，检查每个传感器是否正常，检查数据传输是否正常，并将传感器清零。

2）将制备的碎块通过凹槽型装置自由下落至实验箱中。在碎块堆积过程中，测量堆积体的边界高度、堆积体自然安息角以及最高点距堆积体边界的水平距离，并做好记录。

3）当堆积体边界高度与最下排传感器高度一致时（此时埋深为0 cm）开始计算。此后，每当堆积体边界高度增加10 cm，就记录1 次传感器压力值。

3.3 实验结果

实验过程中，测量碎块密度、堆积体自然安息角、最高点距堆积体边界的水平距离，堆积体各参数见表2。经过对传感器数据的筛选，最终获得的3种堆积体在不同埋深处的传感器数据见表3～表5。

表2 堆积体各参数Table 2 Parameters of accumulation body

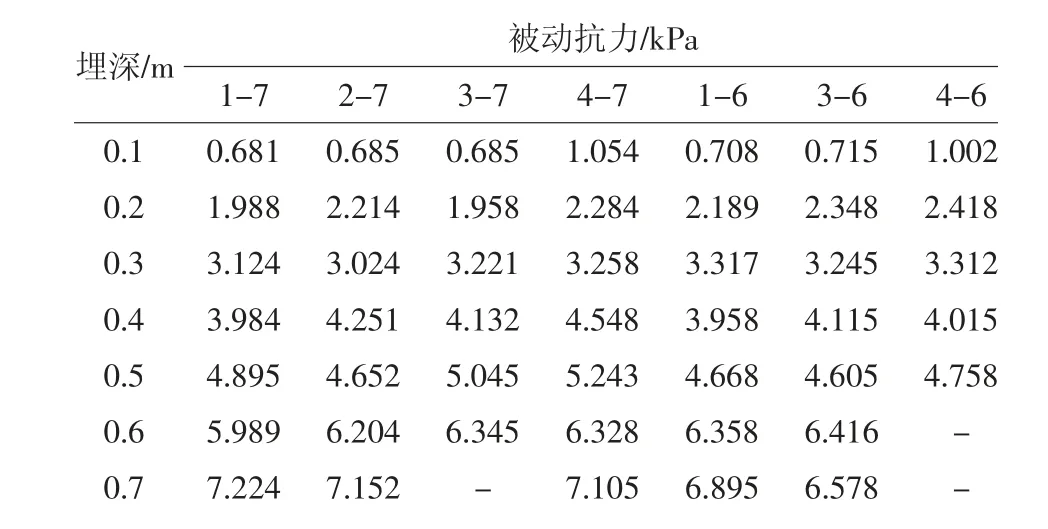
表3 沙粒堆积体边界作用力测量值Table 3 Measurement of boundary force of sand accumulation body

4 实验结果分析

表3～表5 为3 种堆积体边界作用力测定值，为描述边界作用力与埋深的关系，根据数据绘制了边界作用力与埋深关系折线图（图4）。

由表4 和图4（c）可知，20～35 mm 煤块堆积体堆积过程中，某传感器测量数据出现异常值，现剔除

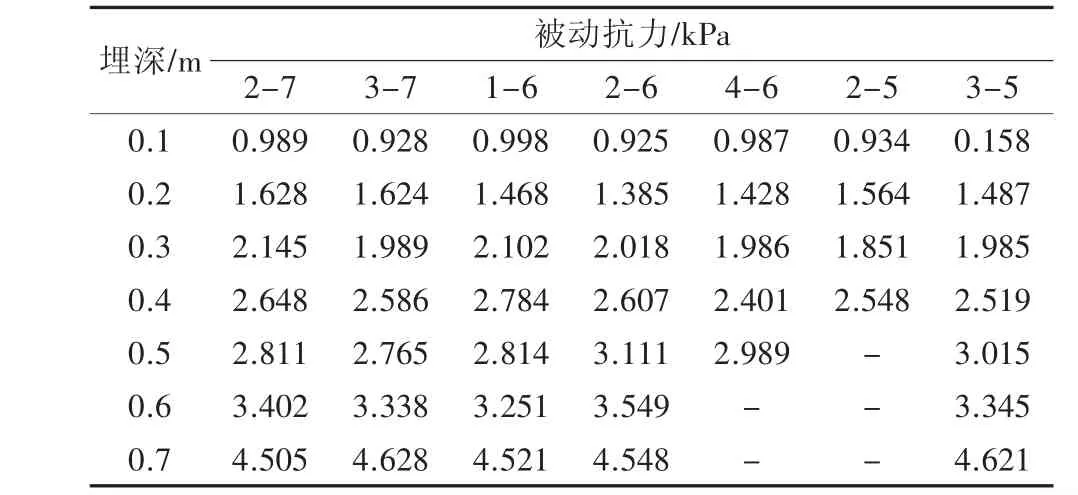
表4 煤块（ 5～20 mm）堆积体边界作用力测量值Table 4 Measurement of boundary force of coal（ 5 ～20 mm） accumulation body

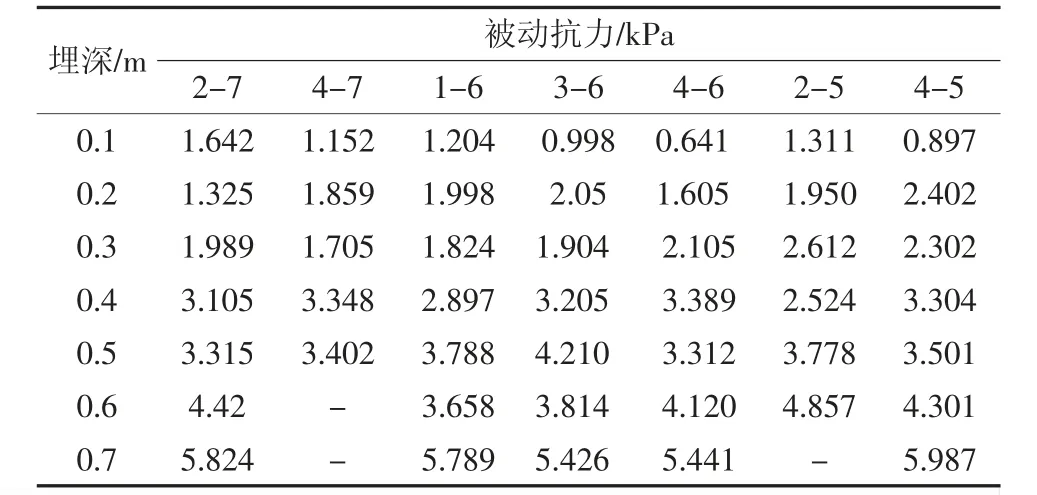
表5 煤块（ 20～35 mm）堆积体边界作用力测量值Table 5 Measurement of boundary force of coal mass（ 20 ～35 mm）

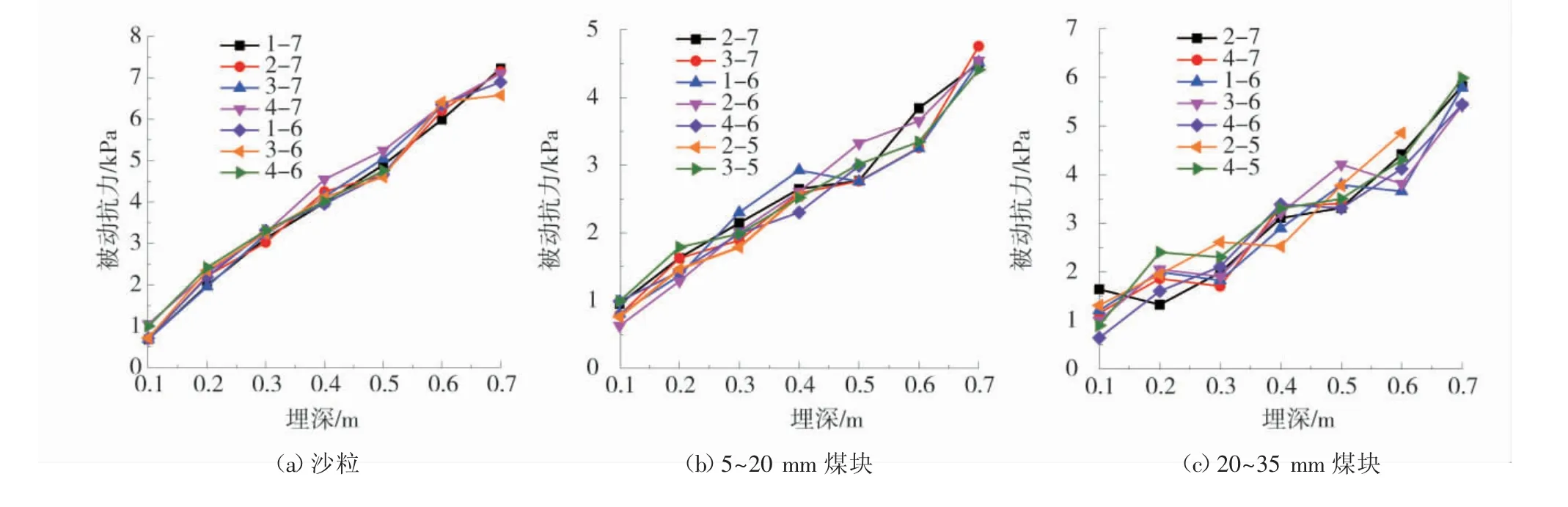
图4 堆积体边界作用力与埋深关系图Fig.4 Relationship between boundary force of accumulation body and buried depth

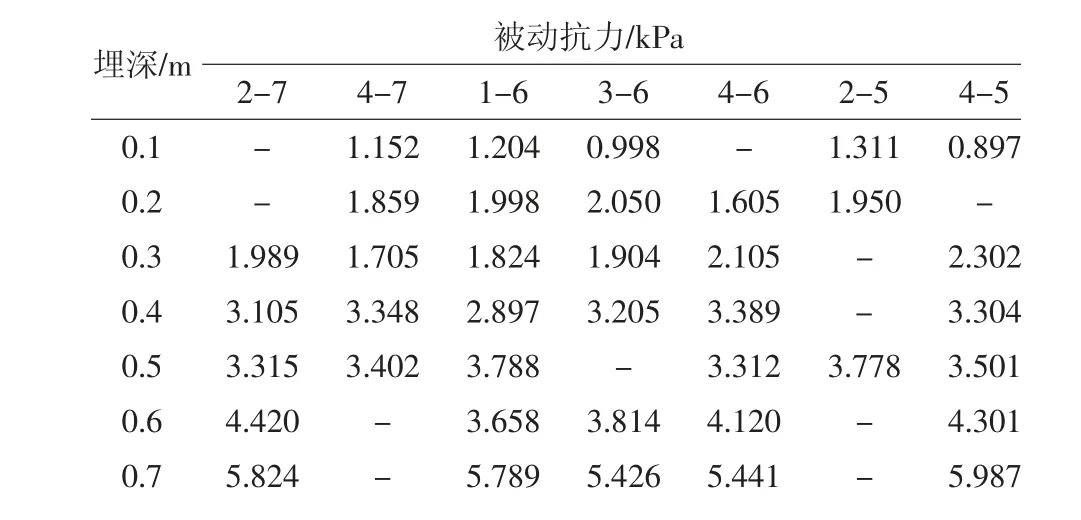
表6 筛选后的煤块（ 20～35 mm）堆积体边界作用力测值Table 6 The measured value of the boundary force of the screened coal mass（ 20 ～35 mm）

将堆积体相同埋深处的不同传感器数据取平均值，得到该埋深条件下堆积体边界作用力实测均值，对表3、表4、表6 中的数据取均值，并运用式（4）计算出不同埋深条件下的被动抗力理论值，进行对比分析，堆积体边界被动抗力测量值与理论值见表7。

根据表7 绘制的被动抗力实测均值与理论值折线图如图5。

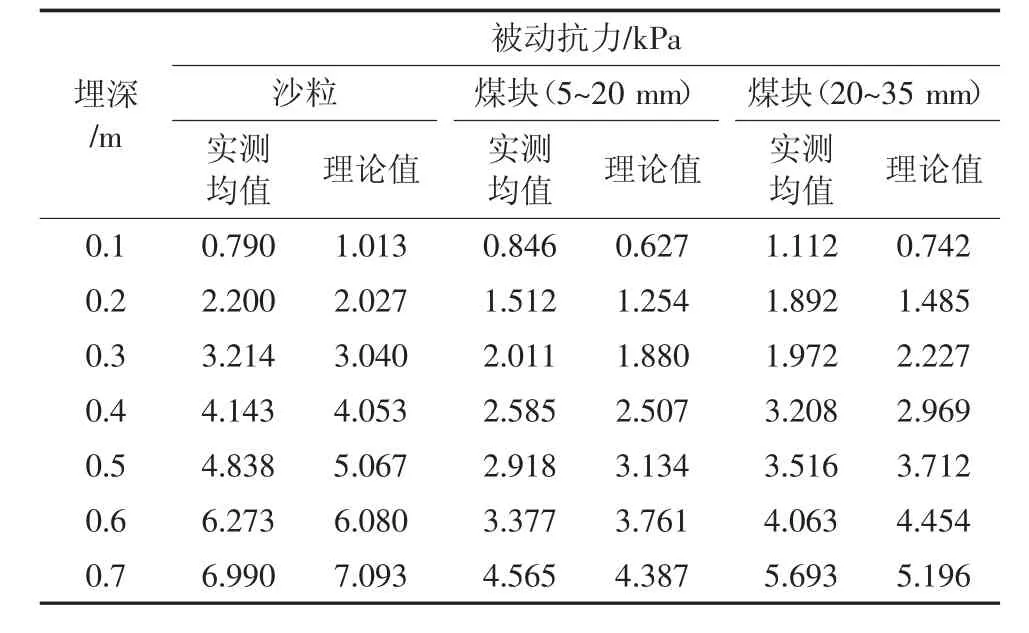
表7 堆积体边界被动抗力测量值与理论值Table 7 Measured and theoretical values of passive resistance at accumulation body boundary

1）根据图5 可知，堆积体边界作用力实测均值折线与理论值折线一致性较高，这说明堆积体边界作用力为被动抗力，源于碎块堆积过程中的滑移效应，堆积体边界被动抗力可通过式（4）计算。

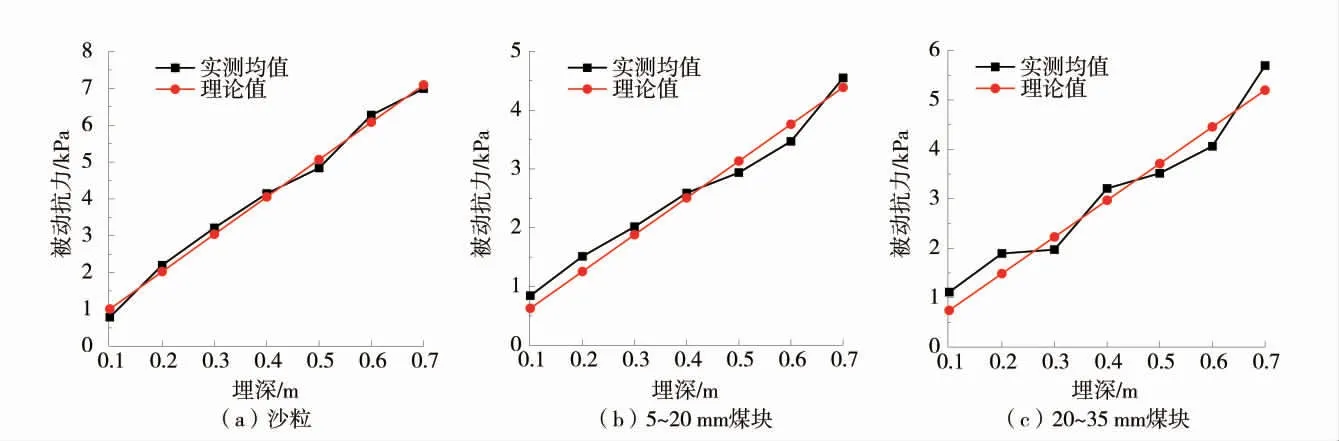
图5 堆积体边界被动抗力实测值与理论值折线图Fig.5 Broken line diagram of measured and theoretical values of passive resistance at accumulation body boundary

2）图5 中还可看出，沙粒堆积体的实测值和理论值差距最小，一致性最高，其次为5～20 mm 煤块堆积体，20～35 mm 煤块堆积体的实测值与理论值偏差较大。图5 显示：沙粒堆积体数据离散性最小，20～35 mm 煤块堆积体数据离散性最大。由表3～表5 可知，沙粒堆积体数据基本无异常值，而20～35 mm 煤块堆积体异常数据较多。以上综合说明：块体粒径越大，实测数据离散型越大。由此推论，式（4）具有一定的适用条件，适用条件取决于碎块粒径与堆积体水平尺寸比值K，K 值越小，式（4）越适合；K值越大，式（4）偏差越大。K 的阈值需要大量实验确定。

3）图4 和图5 共同说明了：随着埋深增加，被动抗力逐渐增大；块体粒径越大，实测值与理论值贴合程度越差。尤其20～35 mm 煤块堆积体异常数据较多，比如2-7、4-7、3-6、4-6、2-5、4-5 传感器数据。另外，某些传感器数据开始正常，到达一定深度后传感器无数据。

5 堆积体形成过程中块体的调整形式

堆积体形成过程中，块体粒径越大，堆积体自组织、重新调整的空间就越大，自组织调整的过程中，块体在堆积体中的位置就不断变化。块体自组织调整主要表现为3 种方式，堆积体形成过程中块体的调整形式如图6。

图6 堆积体形成过程中块体的调整形式Fig.6 Adjustment form of blocks during accumulation formation

1）块体横向移动调整。块体刚开始堆积时会出现图6（a）中情况，块体A 与块体B 之间存有一定的空隙，当块体A 受到向右的力时，块体A 通过横向移动调整，维持堆积体块体内部平衡。其边界被动抗力表现为开始较小，随着堆积体埋深增大，块体横向移动结束，边界被动抗力恢复正常。如表5 中4-6 传感器数据，埋深0.1 m 时，被动抗力很小，随着埋深增大到0.2 m 时，数据恢复正常。

2）块体纵向移动调整。块体堆积过程中，当块体粒径较大时会出现图6（b）情况。块体C 嵌入2 块体之间空隙，但随着埋深增加，块体C 承受的上部块体重力不断增加，块体C 挤入2 块体之间。此时，由于块体C 的挤压作用，边界被动抗力出现增高现象，但随着块体之间的自组织调整，挤压作用逐渐减小，被动抗力逐渐恢复正常。如表5 中3-6 传感器在埋深0.5 m 处的数据和4-5 传感器在埋深0.2 m 处的数据突然增大，这说明块体正在纵向移动调整。

3）块体自身转动调整。如图6（c），个别块体在堆积体边界出现块体D 的临界状态，随着埋深增加，块体D 来自上方块体的重力增大，这种临界状态被打破，块体靠自身转动达到新的平衡，在堆积体边界出现应力集中现象。某些块体自身转动后脱离传感器测量范围，导致传感器数据不存在。如表5中2-5 传感器在埋深0.6 m 时数据增大，埋深0.7 m时，传感器数据不存在。这说明在此期间，块体完成了自身转动调整。

6 结 论

1）断层破碎带巷道段垮落主要以岩石碎块充填为主。垮落形成的岩石碎块，受自重力和块体冲击力的作用，不断进行“自组织”调整，调整方式分为块体横向移动调整、块体纵向移动调整、块体自身转动调整3 种方式。

2）堆积体边界作用力源自于块体堆积过程中的滑移效应，该作用力实为被动抗力。同时，推导了堆积体边界被动抗力计算公式，被动抗力与堆积体密度、堆积体埋深、堆积体最高点距堆积体边界的水平距离、堆积体自然安息角有关。

3）通过自制实验装置测定了堆积体边界被动抗力，验证了公式的正确性。公式具有一定的适用条件，该适用条件取决于粒径与堆积体水平尺寸比值K，K 值越小，公式越适合。