双换能器悬浮传输装置的有限元分析

张 鹏，初红霞，董惠娟，杜 娟，吴东艳

(1.黑龙江工程学院 电气与信息工程学院，黑龙江 哈尔滨 150050；2.哈尔滨工业大学 机电工程学院，黑龙江 哈尔滨 150001)

非接触操控技术作为一种能够传输和操控固体、粉末和液滴等微小颗粒的技术，在物理现象和生化过程的研究中得到了广泛的关注。在众多的非接触传输技术中，声学非接触传输具有诸如非接触、材料独立和不需要对样本预处理等优点。许多团队对非接触超声悬浮和传输技术进行研究[1-5]，实现样本在空气中的悬浮传输。Daniele Foresti等人研制出的线聚焦悬浮器，通过改变辐射面和反射面的距离使小球悬浮并移动37 mm[6]。他们还使用郎之万超声换能器(简称LPT)阵列，实现样本在换能器间的平滑可控移动[7]。本文给出一种用于悬浮传输的悬浮器模型。通过仿真，研究悬浮器几何参数及声参数对声悬浮传输的影响，并进行实验验证。

1 超声悬浮传输装置模型

本文所研究的超声悬浮传输装置由2个超声换能器和1个反射平面组成，如图1所示。反射平面是一个长(L)×宽(W)×高(B)为60 mm×60 mm×5 mm的不锈钢板，其下底面进行镜面抛光处理。超声换能器采用自行研制的半波长单轴式郎之万超声换能器[8]，其变幅杆采用TC4钛合金材料，谐振频率为20 kHz。换能器的辐射端为正方形平面，尺寸为15 mm×15 mm。为了在两个换能器与反射平面间获得平滑的超声声场，选择使用两个参数一致的超声换能器且其辐射面位于同一平面，反射平面与换能器辐射面平行。图中，H表示两个超声换能器与反射平面之间的距离，S表示两个超声换能器辐射面的间距。

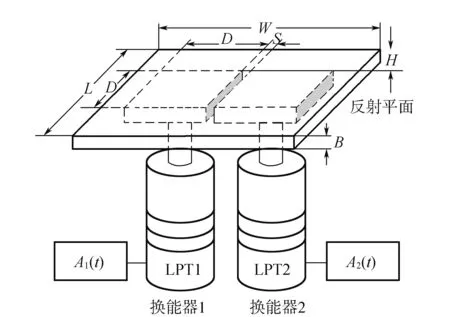
图1 超声悬浮传输装置模型

两个超声换能器分别由自行研制的双路独立输出超声电源进行驱动[9]，双路超声电源的输出信号为幅值、相位、频率独立可调的交流方波A1(t) 和A2(t)。在两路超声信号的作用下，超声换能器的辐射面与反射平面间会产生驻波悬浮声场，物体在声场内声辐射力的作用下悬浮在声场中。通过改变驱动信号的参数，可以控制物体所受声辐射力的大小和方向，进而实现物体的非接触传输。

2 超声悬浮传输装置声场的有限元模型

在超声驻波悬浮现象中，物体之所以能够悬浮在声场中，是因为物体受到了声场中声辐射力的作用。当声场中的物体受到向上的声辐射力等于物体的重力时，物体就能在垂直方向稳定地悬浮在声场中。同时，物体还受到水平方向声辐射力的作用，维持物体在水平方向的稳定。因此，探究物体在声场中的传输运动机理的前提是对驻波声场进行计算分析。

对于超声换能器与反射面之间驻波声场的计算分析，国内外很多学者做了大量研究，本文使用Gor’kov的理论[10]对声场进行分析。Gor’kov在分析超声驻波悬浮时引入了声辐射力的时间平均势能的概念，他指出当小球的半径R远小于其所处声场内声波的波长时，作用在小球上声辐射力的时间平均势U的表达式为

(1)

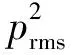
式(1)中的空气质点振动速度v与声场内的声压p存在如式(2)所示关系：

(2)

在声场内悬浮小球的半径Rs、空气密度ρ、声波在空气中的传播速度c已知的前提下，只要能得到驻波声场中的声压分布，即可通过式(1)和式(2)得到声场内声辐射力的时间平均势。进而依据式(3)计算出作用在小球上的声辐射力。

F=-▽U.

(3)

有限元分析(Finite Element Analysis，FEA)是一种利用数学近似的方法对真实物理系统进行模拟的分析计算方法，可以用来进行声场的模拟分析。本文使用美国ANSYS公司研制的有限元分析软件进行超声悬浮传输装置的声场分析与计算。

为了研究超声悬浮传输装置的非接触传输机理，基于图1所示的模型，建立悬浮传输装置中声场的有限元分析二维模型，如图2所示。图2中，取两个换能器所处的平面方向为水平x方向。

图2 超声悬浮传输装置声场有限元分析二维模型

3 声场内声辐射力时间平均势的计算与分析

使用有限元分析软件ANSYS，对图2所示的超声悬浮传输装置声场二维模型进行仿真计算，可以获得悬浮声场内的声压p。

为了简化分析，避免式(1)中小球半径对分析结果的影响，定义声辐射力时间平均势的无量纲形式为

(4)

式中：v0为超声换能器辐射面的最大振速，该值可以通过激光测振仪测量得到。

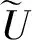
图3 超声悬浮装置声场内无量纲时间声平均势分布(fLPT1=20 kHz,H=8.5 mm,S=1 mm,vLPT1=1 m/s, vLPT2=0)

由图3可知，当声场中的时间平均势最小值点的位置发生水平连续移动时，作用在物体水平方向的力会推动物体跟随其移动，从而实现样本的悬浮传输。

(5)

式中：i表示坐标方向。

时间平均势最小值悬浮点在某一方向的回复力常数越大，该方向的悬浮稳定性越好。

4 换能器辐射面与反射平面之间最优距离的确定

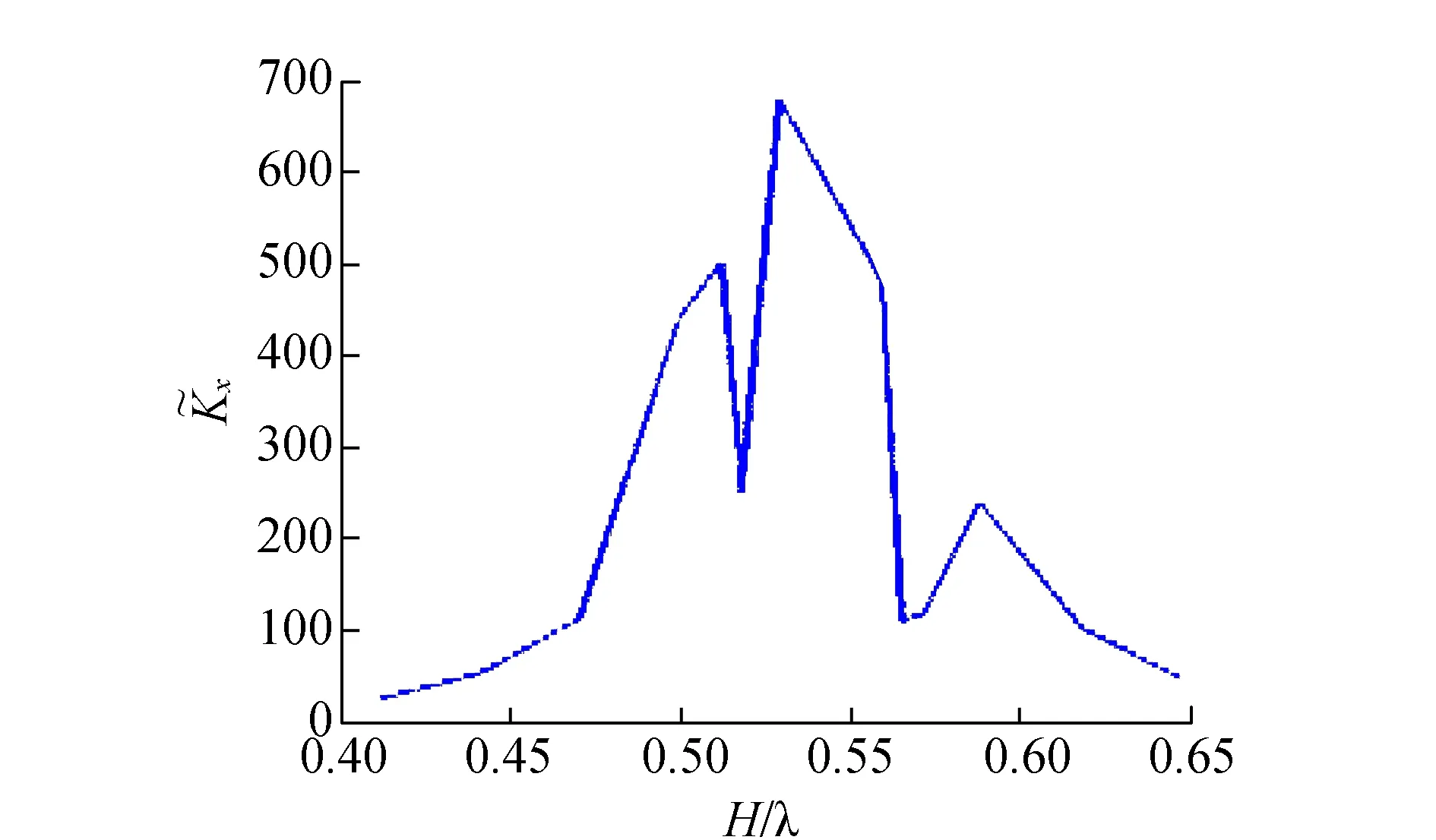
图4 悬浮点的水平方向无量纲回复力系数的变化情况(H/λ=0.412～0.647,vLPT1=1 m/s, vLPT2=0，fLPT1=20 kHz)

值得一提的是，当H=9 mm(H/λ=0.529)时，悬浮点并不处于1号换能器LPT1的上方，而是位于2号换能器LPT2的上方。图 5 给出了在vLPT1=1 m/s，vLPT2=0，S=1，H/λ从0.412变化到0.647时，物体悬浮位置沿x轴方向的变化情况。从图中可以看出，当H/λ取0.412～0.518或0.565～0.647时，物体的悬浮位置位于1号换能器LPT1上方，当H/λ取0.518～0.565时,样本的悬浮位置位于2号换能器LPT2上方。

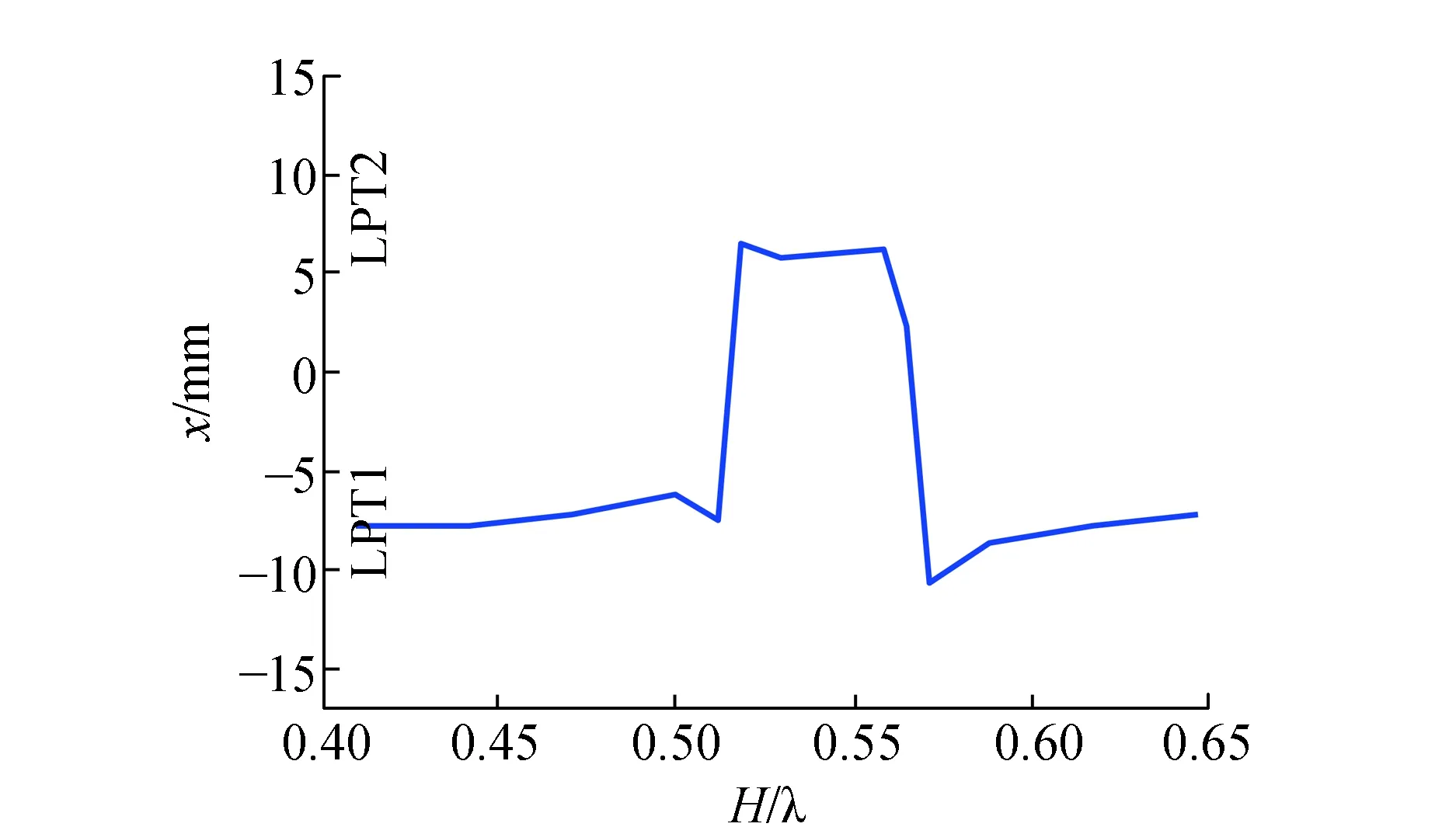
图5 样本悬浮位置沿 x轴方向的变化情况(vLPT1=1 m/s，vLPT2=0，S=1，H/λ=0.412～ 0.647)

5 超声悬浮传输方法

由上述内容可知，当H=9 mm，S=1，vLPT1=1 m/s，vLPT2=0时，样本稳定悬浮于LPT2的上方，该位置为悬浮传输的最佳初始位置。此时，保持LPT1的振速vLPT1=1 m/s不变，将LPT2的振速由0增加到1 m/s，使用ANSYS计算出振速增大过程中的悬浮点位置并绘制出悬浮位置的水平移动情况,如图6所示。图中，物体水平悬浮位置从x=6 mm处移动到了x=0处。这意味着，当声场中悬浮有物体时，物体将随着悬浮点的移动而移动。从图中还可以看出，悬浮点的水平移动距离与LPT2振速的增加近乎成线性关系。

由于换能器辐射面的振速与换能器的驱动信号幅值成正比，因此，图6中LPT2的振速由0增加到1 m/s的过程可以通过改变换能器驱动信号幅值的方法来实现。同时，依据图6的仿真结果可知，当两个换能器辐射面的振速相等时，物体悬浮在水平方向0处，此时，若将LPT1的振速由1 m/s逐渐降低至0，物体将由0处向LPT1上方移动，当LPT1的振速降为0时，物体会停留在LPT1的上方。据此，可以得到一种在H=9 mm，S=1的条件下，控制样本从LPT2移动到LPT1的方法,如图7所示。

图6 LPT1振速不变，LPT2振速由0增加到1 m/s时样本悬浮位置的水平移动情况

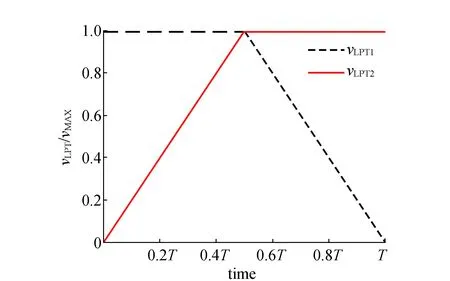
图7 控制物体从LPT2移动到LPT1过程中两个LPT的振速变化

图中，T表示一个传输周期，即物体从LPT2移动到LPT1的时间。vMAX表示换能器驱动信号幅值输出为最大时的辐射面最大振速，由于两个换能器以及驱动换能器的两个超声电源参数一致，因此，两个换能器辐射面的最大振速相等，即vMAX1=vMAX2=vMAX。图中使用最大振速vMAX对换能器的振速进行归一化处理。当time=0时，调节换能器驱动电源，使得LPT1的驱动信号幅值输出最大，对应振速为vLPT1=vMAX，LPT2的驱动信号幅值输出0，对应振速为vLPT2=0，此时，物体悬浮在LPT2的上方。随着LPT2的驱动信号幅值增大，vLPT2也增大，样本向悬浮器的中间位置移动。当time=0.5T时，两个换能器的驱动信号幅值均为最大值，即vLPT1=vLPT2=vMAX，物体移动到悬浮器的中间。之后，保持vLPT2=vMAX不变，将LPT1的驱动信号幅值从最大值减小到0，vLPT1从vMAX减小到0，物体由悬浮器的中间位置向LPT1的上方移动。当time=T时，vLPT1=0，vLPT2=vMAX，物体移动到LPT1的上方，完成一次传输过程。

依据上述方法，使用课题组研制的单轴超声换能器和超声电源构建如图1所示的超声悬浮传输装置，对聚苯乙烯小球进行悬浮传输实验。实验结果与仿真结果吻合较好，图8为实验照片。

图8 聚苯乙烯小球的悬浮传输

6 结束语

本文对用于悬浮传输的双换能器超声悬浮传输装置进行了有限元分析，研究了换能器与反射面间的距离及两个换能器辐射面的振速对悬浮传输过程的影响，提出了一种通过改变换能器驱动信号幅值来实现物体悬浮和水平移动的方法。