异方差下正则化Expectile回归的变量选择
李顺勇,卫夏利,张晓琴
(1.山西大学 数学科学学院,山西 太原 030006,2.山西财经大学 统计学院,山西 太原 030006)
0 引 言
回归是统计学中刻画数据结构常用的方法之一。在回归建模过程中,随着数据维度越来越高,变量选择发挥的作用越来越重要,一旦选入与因变量无关的自变量,估计和预测精度就会下降,模型的泛化能力将会变差。现阶段变量选择的方法已经从传统的离散最优子集回归发展到正则化框架,除已知的最小绝对收缩和选择算子(Lasso)[1]外,随着光滑削减绝对偏差(SCAD)[2]的提出,Oracle性质成为变量选择好坏的评价指标。2006年,ZOU H[3]提出自适应Lasso改进Lasso不具有Oracle性质的缺点。此外,还有常用的正则化惩罚函数,如弹性网[4]和MCP[5-6],它们在最小二乘回归中应用已有大量成果。
在实际建模中,另一个总被忽略的重要特征是异方差性[7]。传统的最小二乘回归由于对误差项的假设,使得它在处理异方差时是失效的。分位数回归[8]作为一种分析异方差的方法,在回归过程中能够探究给定自变量时因变量的整个条件分布[9]。WU Y等[10]研究了惩罚分位数回归的变量选择,并给出误差项独立同分布时估计量的渐近性质;WANG L等[11]通过超高维数据中的正则化稀疏分位数回归分析了异方差性。但分位数回归存在3个缺点,即不可微性、类高斯误差分布的无效率性和绝对值损失函数带来的计算压力。另一种检测异方差的方法是基于非对称L2范数提出的非对称最小二乘回归,也称为Expectile回归,它表现出许多优良的性质,使回归方法有了进一步的拓展和延伸[12-14]。回归误差服从高斯分布时,GU Y等[15]采用正则化的Expectile回归分析高维数据中的异方差问题;赵军[16]在研究正则化Expectile回归时指出,回归误差服从高斯分布这一条件在实际中不易满足,误差项有时具有有限阶矩甚至重尾的情况,故研究了当回归误差具有有限阶矩条件下,带SCAD正则化的Expectile回归的变量选择以及在检测异方差上的有效性;LIAO L等[17]用SCAD和自适应Lasso作为惩罚项,研究了正则化Expectile回归在回归误差存在有限阶矩时的变量选择,同时给出了误差项独立但不同分布下的Oracle性质。
MCP惩罚作为一种非凸惩罚函数,已被证明在理论和实践上对变量选择和参数估计是有效的,这一方法解决了近似无偏估计和如何找到凹度最小惩罚计算困难的问题。考虑到MCP在变量选择和参数估计上的优良性,将MCP惩罚函数引入到Expectile回归中,其诱导的估计量是否仍然具有良好的性质是一个重点。因此,本文在研究回归误差项独立同分布假设的基础上,构建了在有限阶矩假设下独立但不同分布的误差项,具有MCP惩罚的正则化Expectile回归估计量的渐近性质。
1 Expectile回归基本概念及正则化模型
分位数回归和Expectile回归分别是基于非对称L1范数和非对称L2范数而提出的。在给出相应的优化问题之前,首先给出一个随机变量Z∈R的τ均值,
Eτ(Z)=arg mina∈REΨτ(Z-a),
式中:τ∈(0,1),为Expectile水平;Ψτ(.)为非对称平方损失函数,定义为
Ψτ(u)=|τ-I(u<0)|u2,
(1)
其中,I(.)为示性函数。
考虑线性模型
Y=Xβ+ε,
式中:Y=(y1,…,yn)′为一个n维因变量;X=(X1,…,Xp)为n×p维自变量矩阵,该矩阵也可写作X=(x1,…,xn)′,其中xi=(xi1,…,xip)′,i=1,2,…,n;β为p维未知参数向量;ε为误差项。
考虑到变量选择,需对模型进行一定的稀疏性假设,即只有一小部分自变量影响因变量的分布。不失一般性,假设自变量中前q个为重要变量,其余的为噪声变量,即X=(X1,X2)′∈Rp,X1∈Rq,X2∈Rp-q分别对应重要变量和噪声变量,相应的回归系数真值为β0=(β10′,β20′)′,其中β10是非0的q维向量,β20是p-q维的0向量。此时β=(β1′,β2′)′,xi=(xi1′,xi2′)′。线性回归模型变为稀疏模式
对一些预先设定的τ∈(0,1),随机误差εi的τ均值为0。
基于上述模型,Expectile回归定义为极小化函数,即
τ∈(0,1),β∈Rp,即Expectile回归系数估计量为
其中,Ψτ(.)为非对称平方损失函数,定义见式(1),τ=0.5时,Expectile回归即为OLS回归。
分位数回归定义为极小化下式:
其中,β∈Rp,α∈(0,1),rα(.)定义为
rα(u)=|α-I(u≤0)|.|u|。
(2)
分位数回归基于非对称L1范数,对回归模型中正负残差赋予不同的权重,使其在回归过程中能够探究给定自变量时因变量的整个条件分布。当考虑不同的条件分布片段时,相关自变量集合可能发生变化。导致异方差存在的其中一个原因是线性模型中残差项受到自变量的影响。因此,通过不同分位数水平下线性模型中自变量集合的变化,识别出引起异方差的自变量,进而可以有效地检测模型的异方差性。
由于分位数回归中损失函数使用L1范数,而Expectile回归中采用L2范数,故后者比前者对离群点更敏感,这为Expectile回归在检测异方差性方面比分位数回归更显著提供了理论基础。
目前对非凸惩罚研究较为广泛的有SCAD[2]和MCP[5],其中MCP惩罚函数为
(3)
它的导数为
(4)
式中:sgn(.)为符号函数;λ和γ为正则化参数,γ>1。
考虑惩罚Expectile回归模型的目标函数
(5)
式中,pλ(|βj|)为相关惩罚函数。
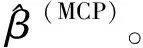
2 渐近性质
本节给出回归误差项独立但不同分布下带有MCP的Expectile回归理论性质。先给出下列条件[10,16-17]:

条件2:X的行向量{xi,i=1,2,…,n}是确定性序列,假设存在正定阵∑,使得


条件4:假设存在正定阵∑gτ,∑hτ,使得

gτ(εi)=Ψτ′(εi-t)|t=0=-2τεiI(εi≥0)-
2(1-τ)εiI(εi<0),
hτ(εi)=Ψ″τ(εi-t)|t=0=2τI(εi≥0)+
2(1-τ)I(εi<0),i=1,2,…,n。
基于随机误差项独立但不同分布的假设,带MCP的Expectile回归系数估计量有如下定理。
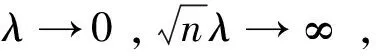
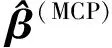

(6)
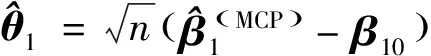
(7)

在Rq的任意紧集上一致成立而且不依赖于θ1。
因此n→∞时,
代入式(7)可知,j=1,2,…,q时,
op(1)+o(1),
则
那么


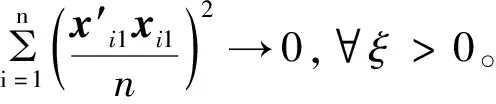
由林德伯格中心极限定理知

由Slutsky定理得
则

3 数据模拟
为了与带有MCP的正则化Expectile回归方法进行比较,同时考虑带有SCAD的Expectile回归(E-SCAD)[16-17],带有自适应Lasso的Expectile回归(E-AL)[17]和带有SCAD的分位数回归[10](Q-SCAD)。由于SCAD和MCP惩罚函数在优化问题中存在非凸性,应用CCCP算法[10-11,16-17]解决优化问题,这是一种适用于优化函数可分解为凸函数和凹函数之和的算法。先通过局部线性逼近算法(LLA)寻求目标函数的局部上紧凸函数,接着通过连续极小化局部上紧凸函数寻求一个局部极小值,下面分别给出E-SCAD,E-AL,Q-SCAD的优化问题:
(8)
(9)
(10)
其中,惩罚函数pλ(.)定义为
pλ(|βj|)=λ|βj|I(|βj|≤λ)-
为了研究模型具有异方差时提出方法在变量选择和检测异方差上的表现,模拟数据从下述线性模型中产生:
Y=1+X1+X2+X3+(1+X3),
(11)
其中X2=X1+X3+Z,X1和Z均从独立标准正态分布中产生,X3从[0,1]上的均匀分布中产生,X1,X3,Z和ε之间相互独立。残差项受到自变量X3的影响,所以该线性模型具有异方差性。


图1 各变量与残差平方的散点图
为了考查误差具有有限阶矩的表现,考虑随机误差项的2种分布,即标准正态分布和重尾分布t(10)。通过增加服从标准正态分布的独立噪声变量,考虑2种不同样本量和自变量维度,分别为p=10,n=100和p=20,n=200。对于惩罚Expectile回归,考虑不同的Expectile水平τ分别为0.1,0.25,0.5,0.75,0.9。当给定具体分布时,计算与τ值一一对应的分位数水平。

表1列出了在式(11)的数据生成下,误差项服从标准正态分布假设时,几种方法在样本量n=100自变量维度p=10的模拟结果。样本量n=200自变量维度p=20的模拟结果在表2中列出。误差项服从t(10)分布时的模拟结果分别列于表3和表4。

表1 标准正态分布假设时p=10,n=100模型(11)模拟结果

续表1
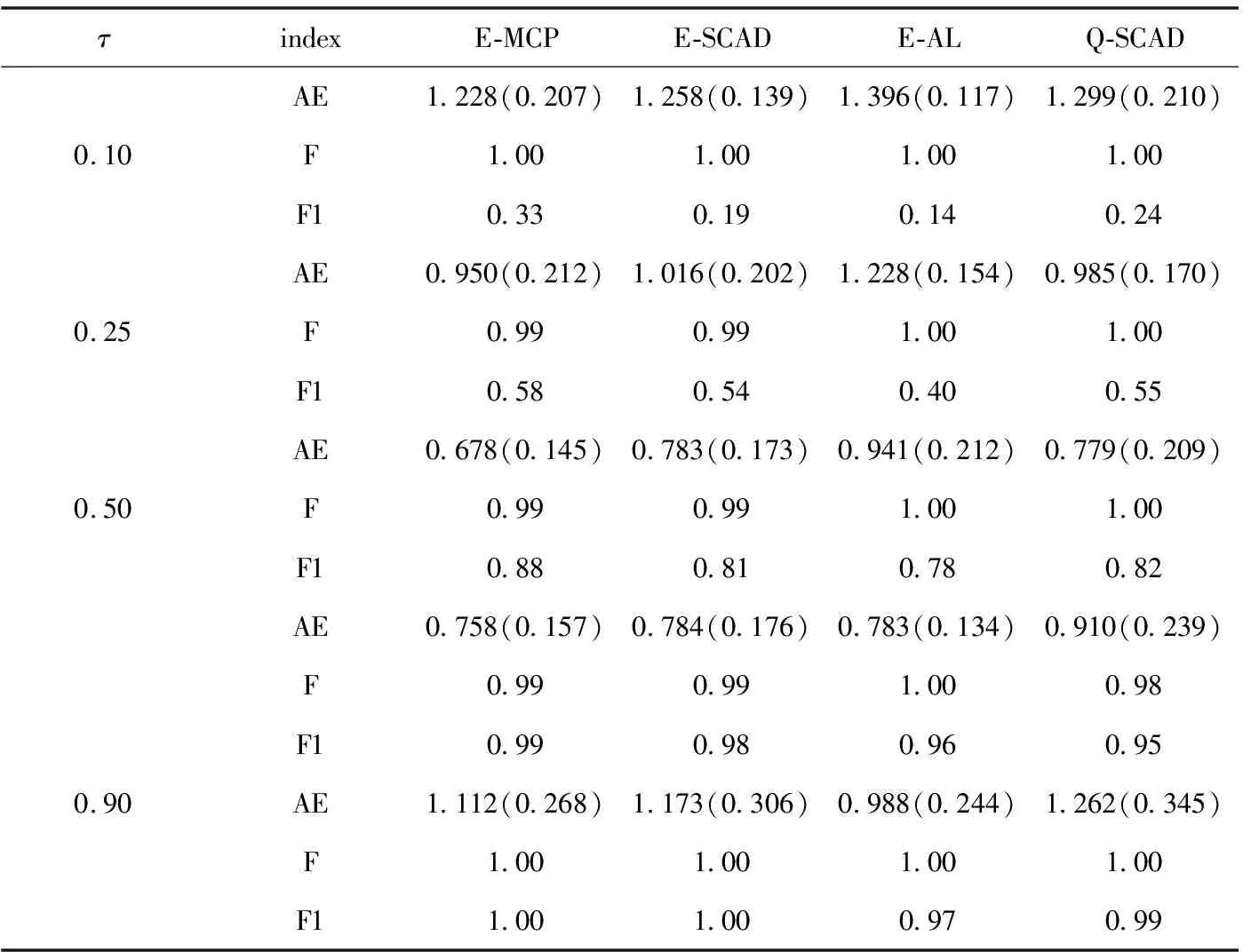
表2 标准正态分布假设时p=20,n=200模型(11)模拟结果

表3 t(10)分布假设时p=10,n=100模型(11)模拟结果

表4 t(10)分布假设时p=20,n=200模型(11)模拟结果
表1~4显示本文提出的方法在模拟中产生更小的绝对误差,其中括号内为基于100次模拟结果所产生的方差。考虑到X3在式(11)中是一个既对均值又对方差有影响的自变量,所以先得到在100次模拟中X1,X2(仅对均值产生影响的自变量)的变量选择结果。对比之下,4种方法均可以趋于1的概率选取到重要变量。就X3而言,从表1~4中的F1结果发现,随着Expectile水平τ增加,对X3的选取频率呈明显增长趋势,τ=0.9时选取到这一自变量的频率较高,此时X3可能是引起异方差现象的自变量。
基于上述结果,按照下述模型生成数据,执行新的模拟
Y=1+X1+X2+(1+X3)ε,
(12)
自变量X1,X2,X3的生成同式(11),在设定X3只是对方差有影响的自变量,表5给出在式(12)下误差项为标准正态分布假设时X3的变量选择的结果。
从表5可以看出,随着τ变化,对X3的变量选择结果并没有直接增长。τ=0.5时,选择X3的频率很低,而随着τ∈(0,1)向0和1的方向变化,选中X3的频率逐渐增加。而X3正是只对方差项有影响而对均值项无影响的自变量,本文提出的方法在选择X3上比其他方法均有较好表现。

表5 标准正态分布假设时p=10,n=100模型(12)模拟中X3的选择结果
通过对比证明,在自变量只影响均值时,本方法可以趋于1的概率选取到重要变量,当随着Expectile水平τ的变化,自变量的选取频率呈增长趋势时,该自变量既对均值有影响,又对方差产生影响。τ=0.5时选取概率极低,而在其他水平下增高,因此,该自变量只对方差有影响。综上所述,模拟试验结果表明,本文提出的方法在变量选择中能产生更小的误差,且比其他方法以更优的概率选取到引起异方差的自变量,从而可有效地检测出异方差。
4 结 语
本文基于Expectile回归对回归模型中正负残差赋予不同的权重,通过不同的Expectile水平,在回归过程中能够探究给定自变量时因变量的整个条件分布,已有异方差文献多基于误差项服从独立同分布假设或者随机误差项服从正态分布,本文将该假设弱化为随机误差项独立但不同分布,且具有有限阶矩,并建立了相应的带有MCP惩罚项的Expectile回归估计量的渐近性质,得到在一定的条件下相应估计量的Oracle性质。数据模拟结果表明,本文提出的方法在变量选择上表现优良,并且能够通过自变量集合的变化有效地检测出异方差。

