改进模板匹配的快速识别算法

李长有，付惠琪，陈国玺

(1.河南理工大学 机械与动力工程学院，河南 焦作454000；2.焦作市技师学院 电气工程系，河南 焦作 454000)

0 引 言

模板匹配是计算机视觉领域中对目标图像进行识别和理解的重要方法[1]，它是对模板图像和目标图像进行相似度的检测[2]。传统模板匹配算法在匹配过程中对噪声比较敏感，因此，消除噪声的干扰至关重要[3]。由于传统模板匹配在运算效率和鲁棒性方面存在一定的缺陷，近年来，许多学者对其进行了大量的研究。N.D.Salih等[4]提出利用快速FFT变换结合区域生长分割进行图像的目标识别；YE Y等[5]利用像素的局部特征，结合三维快速傅里叶变换在频域上进行相似性度量；LI C等[6]提出一种图像相关与卡尔曼预测结合的方法，加快目标的识别速度；B.G.Shin等[7]利用基于灰度索引表的快速稳健模板匹配算法，可以在噪声环境中找到图像的特定区域；LIU B等[8]提出一种八角形星型查询模板算法，该算法大大减少了图像搜索空间，从而加快了算法的运行速度；S.K.Sahani等[9]利用两阶段搜索法对图像进行快速识别，有效地确定相关点的精确性和鲁棒性；A.Emlek等[10]利用可变窗口对图像边缘可变区域进行匹配，从而加快了算法的匹配速度；J.Y.Kim等[11]利用改进的hausdorff距离作为相似性度量函数，降低了算法的复杂程度。上述方法在较强噪声环境下，匹配速度和准确率往往不太理想，并且其相似度函数具有一定的复杂性，因而降低了算法的运行速度。为了更好地降低较强噪声的影响，改善算法的运行速度，本文提出一种改进模板匹配的快速识别算法。该算法采用改进的低通滤波器滤除图像中的噪声，使用同伦骨架算法对二值图像进行细化，减少冗余的边缘点，采用加权的Hamming Distance作为相似度检测函数，减少算法的复杂程度，并且采用设置的阈值，改善算法的运行速度。

1 算法原理

1.1 改进滤波器原理

针对传统模板匹配在较强噪声匹配过程中出现的误匹配现象，提出一种改进的线性平滑滤波器对图像进行噪声滤除，其原理是利用n×n的相同元素模板A和模板覆盖下的原图像f(x，y)运算得到子图像f1(i,j)，中心像素为E(i，j)，然后子图像与单位矩阵I的列向量运算，可以得到新的图像f2(i,j)，f2(i,j)与单位矩阵I的列向量再运算得到图像f3(i,j)，用此时图像f3(i,j)的平均值与中心像素E(i，j)比较，数学模型为

(1)

β1=f1(i,j)*i1=

[a11x11a21x21…an1xn1]T，

(2)

(3)

由公式(2)可以写出剩余项，即f2(i,j)，则

(4)

则去掉最大最小像素的f3(i,j)为

f3(i,j)={sort[f2(i,j)]}*I(i3,…,in×n-3)=

[f2max(i,j),f2(i,j+1),…,f2min(i,j+(n×n)-1)]*

[i3,…,in×n-3]=[f2(i,j+2),…,f2min(i,j+

(n×n)-3)]，

(5)

(6)

(7)

式中：(i1,i2,…,in)为单位矩阵I的列向量；sort为排序函数；E(i,j)为图像的中心点像素。

文中相同元素矩阵A使用的是3×3矩阵。

1.2 同伦骨架算法细化边缘

骨架思想由H.Blum[12]引入，并称之为中轴变换或骨架。基于“草地火焰”模型和最大球骨架[13]得到的骨架是不同伦的，即不保持原来集合的连通性，并且在离散平面内骨架线条要宽于一个像素。

图像细化和粗化是击中击不中变换的一个应用，对于图像f(x,y)用复合结构元素M进行顺序细化时可以得到一个同伦的目标骨架。

顺序细化的结构元素L(n)和D(n)如图1所示，利用图1中的8个结构元素对图像多次细化，图像能够保持拓扑同伦且收敛于断面为单个像素宽度及8邻域是连通的目标骨架。

图1结构元素L={L1,L2,L3,L4}分别消除目标上方、右方、下方和左方的外层图像，D={D1,D2,D3,D4}分别消除目标右上、右下、左下和左上的外层图像。其中“*”为该元素在匹配过程中没有被用到，取值可以任意。

同伦骨架[14]算法能够保持图像骨架集合的连通性和拓扑性，其定义为

E{f(c,y),L,D,k}=f(x,y)Θ{M(n)}k=

{(((…((f(x,y)ΘL1)ΘD1)…)ΘL4)ΘD4)}k，

(8)

式中：Θ为结构元素与图像之间的腐蚀运算；k为细化次数，图像复杂程度不同，k值不同。

1.3 改进的Hamming Distance

为了解决特征向量相似度函数过于复杂，并加快算法的运行速度，本文提出用改进的Hamming Distance(海明距离)作为模板图像和目标图像的相似度函数，以此减少算法的复杂程度，从而提高运行速度。

Hamming Distance[15]是用来计算两个等长二进制序列中对应位数不同的数字位置个数，假设g={g1,…,gm}和v={v1,…,vn}是两个不同点集，当m=n时，海明距离Hd公式为

Hd=∑(g⊕v)，

(9)

式中，符号“⊕”为两个序列异或运算。

为了更好地降低图像噪声带来的影响，本文采用加权海明距离作为相似度函数，当模板图像大小为m×n时，则其数学模型为

(10)

式中：round为取整函数；Gtemplate、Vsub-image分别为模板图像和目标图像子图像。

1.4 阈值的确定原则

模板匹配是模板图像在整幅目标图像上逐行逐列进行移动并进行相关性计算的过程，在模板图像移动过程中有很多非目标区域的像素也参与运算，因此,降低了算法的运行速度。为了更好地减少算法的运行时间，在进行模板匹配时把大小为m×m的模板分成两块并与设置的阈值Tk进行比较，以此提高算法的运行效率。将模板图像分成两块，并取出R=round[(m×m)/2]个像素构成的图像，用相似度检测函数计算出的向量距离值与阈值进行比较，从而减少算法的运行时间，提高运行效率。通过实验选取阈值Tk的基本原则为

(11)

本文算法的流程图如图2所示。

图2 算法流程图

2 结果与分析

为了验证本文算法的有效性，选择52幅不同背景下的图像作为实验对象，并在图像中加入了σ1=0.08的椒盐噪声和均值m=0.02、方差v=0.001的高斯噪声。使用MATLAB R2016a软件平台，并用Intel Core i5-2450M CPU@2.5 GHz处理器对不同背景的噪声图像进行目标识别。其中在传统模板匹配过程中，使用传统的中值滤波器对图像进行降噪，文献[11]中Canny算子的高低阈值人工设置，其高低阈值分别为0.4和0.16，高斯滤波器中的σ=0.9。本文算法使用N.Otsu[16]确定Canny算子的高低阈值，与其他模板匹配算法在运行效率和算法鲁棒性方面进行比较，实验效果对比如图3所示。通过实验对比图能够很容易看出，本文算法在目标识别过程鲁棒性较好，为了更好地说明本文算法的有效性和鲁棒性，表1列出了算法的平均运行时间和识别准确率。

图3第一列表示目标图像和模板图像，红色标识的为模板图像;第二列是噪声环境下传统NCC算法的效果图，该算法对不同噪声图像目标识别有较好的鲁棒性，但从表1可以看出，该算法在识别准确率方面存在一定缺陷，并且平均运行时间比其他算法运行时间长，从而导致该算法运行速度比较慢；第三列是文献[6]中FNNPROD算法的效果图，该算法对噪声的鲁棒性相对较差，存在一定误匹配现象。但从表1可以看出，该算法的平均运行时间相对较少，运算速度比较快；第四列是文献[11]可改进的hausdorff算法效果图，对噪声的鲁棒性比较差，出现了误匹配现象，但从表1可以看出，该算法的平均运行时间较少，运行速度较快；第五列是本文算法的效果图，从图3可以看出，本文算法对噪声有较好的鲁棒性，表1更进一步说明了本文算法的优越性，算法的识别准确率与平均运行时间较少，运行速度较快。

表1 算法的有效性对比

图3 实验效果对比

Fig.3 Comparisons of experimental results

为了更进一步说明本文算法的鲁棒性，对不同背景下的噪声图像进行实验，本文滤波器与传统滤波器滤除噪声后的效果图如图4所示。从图4可以看出，本文滤波器能够滤除图像中较强的噪声，并根据文献[17]对图像质量的评价方法评价本文滤波器滤除噪声的能力，以及滤除噪声后的图像与目标图像的相似程度。图5所示分别计算了图像峰值信噪比(PSNR)和结构相似性指数测量(SSIM)，从而佐证本文算法对噪声的鲁棒性。其中PSNR表示滤波器对噪声的去除能力，其值越大，表示对噪声的滤除能力越强，图像的失真也越小。从图5可以看出，本文设计的滤波器比高斯滤波器和均值滤波器的PSNR值都大，与中值滤波器相差不大，表明本文算法的去噪声能力较强，图像在滤除噪声后比较清晰。

图4 本文滤波器与传统滤波器对比

SSIM是度量两幅图像的相似性，它是通过检测图像3个因素(相关性、亮度和对比度)的损失，比较两幅图像的相似性，其值介于-1到1内，计算数值越接近1，表示图像的相似度越高，图像噪声的滤除越好。从图5可以看出，本文算法的SSIM值相对较大，表明本文算法对噪声消除后的图像失真相对较小，从而佐证了本文算法的鲁棒性。

3 结 语

本文提出的快速识别算法对较强噪声干扰图像能够很好地识别出目标位置，并且算法运行速度较快。通过改进的低通滤波器滤除噪声，降低噪声对图像的干扰，提高了算法的识别率，使用改进海明距离作为图像的特征向量检测函数，降低了算法的复杂程度，并且提出了阈值的选取原则以及使用同伦骨架算法，大大提高了算法的运行速度。因此，本文算法可以弥补传统NCC算法、文献[6]和[11]算法的不足，并且能够提高算法的运行速度和识别准确率，可为目标识别、安防监控和其他工业应用提供一定参考。

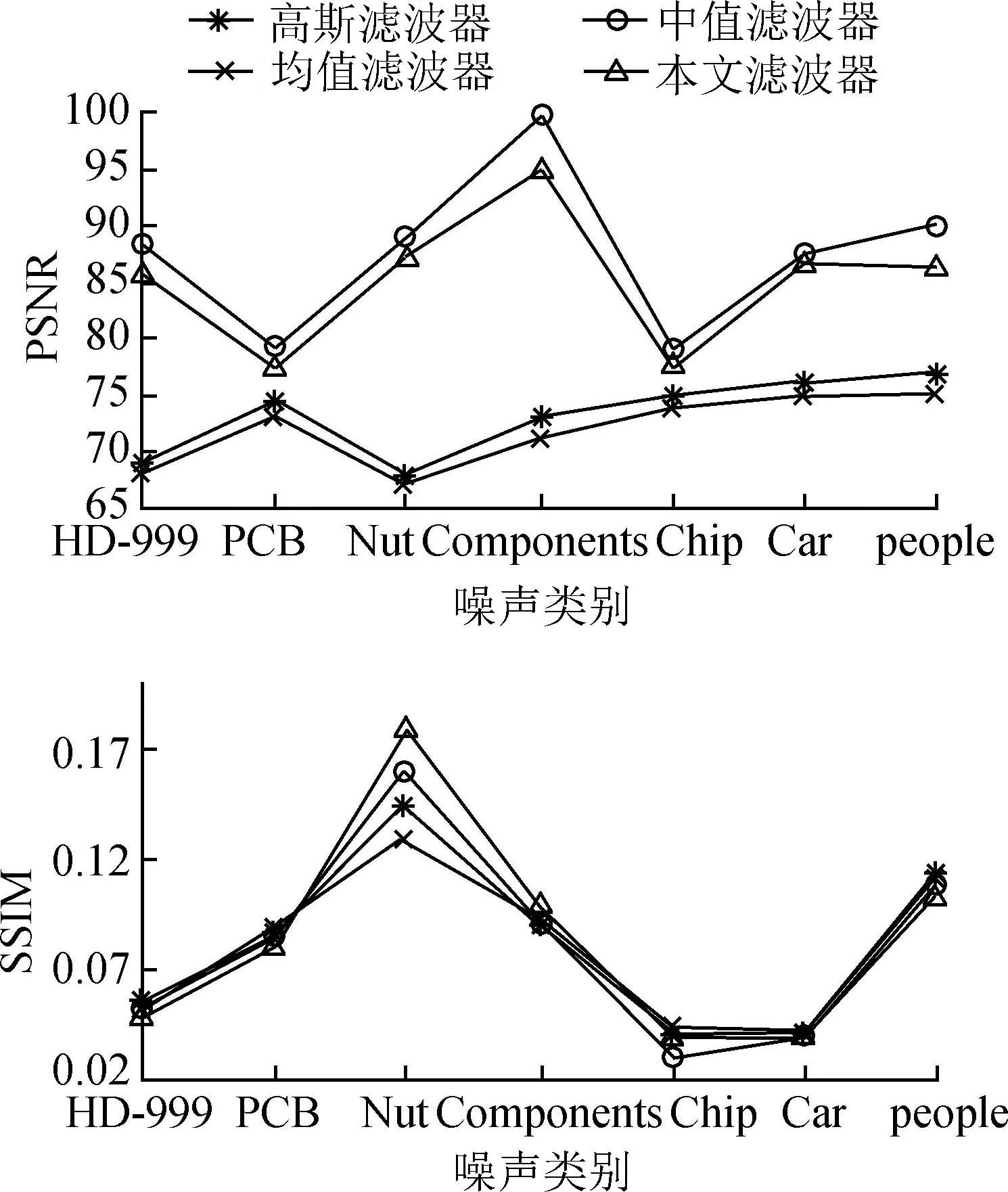
图5 不同滤波器噪声滤除能力对比