基于遗传-拟牛顿混合算法的地下震源定位

宋运忠,王仁辉

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

0 引 言

随着现代无线网络、通信技术和计算机技术等的快速发展，人们对无线通信技术的要求也越来越高。传统的单一应用功能已经远远不能满足现代社会的需求，比如在深海勘探、森林勘探、高山平原勘探、智能医疗和智能家居等方面。在这些环境中，无线传感器网络的应用得到了迅速的发展，多功能的传感器网络也随之而生，比如运用传感器网络进行动植物生活习性的监测、对未知声源和震源的定位、深海勘探等。

在运用无线传感器网络进行定位时，第一个重要的环节是各个节点需要进行时钟同步，需要用精准的时间戳(消息数据部分的传送时间与当前时间差值)进行准确定位。目前已有参考广播同步[1]、梯度时间同步协议[2]等传感器网络的时钟同步算法被用来进行时钟同步，且效果非常好。D.Pazo等[3]主要研究了脉冲耦合在生物振子方面的应用；O.Simeone等[4]对一类无线传感器网络的时钟同步进行了讨论，并分析了同步的鲁棒性；R.Gentz等[5]讨论了脉冲耦合无线传感器网络时钟同步的可扩展性；WANG Y Q等[6]提出了优化的相响应函数，该响应函数能快速实现脉冲耦合。

第二个重要的环节是定位。通常，最简单的无线传感器网络定位方法就是为各个节点装载全球定位系统(global positioning system，GPS)接收器，用以确定节点位置。但是，由于成本、各个节点能量及GPS对环境有一定要求等诸多条件的限制，实际中每个节点不可能都装备GPS接收器，即使都装备，也不能精确定位到毫米级别。所以本文使用到达时间差(time difference of arrival，TDOA)的定位方法对地下未知震源进行定位。传统的TDOA定位方法是：两种不同传播速度的无线信号在发射节点和接收节点之间进行传播，测得到达时间差，随之计算信号点到接收点的距离。常见的无线传感器网络测距方法包括：到达时间[7-9](time of arrival，TOA)测距，该法要求硬件之间有较高的时间同步；到达角度[10](angle of arrival，AOA)测距，该法要求传感器节点拥有测量角度的功能。

随着传感器网络和定位技术的快速发展，人们对定位方法的研究越来越多，定位精度的要求也越来越高。迄今为止，陆地上相关技术发展已比较成熟[11-12]，但是对瓦斯定位及对未知震源的定位技术还不够成熟，为此，本文提出一种基于遗传-拟牛顿混合算法的远场地下震源TDOA定位方法。即利用震源发出的脉冲信号到不同传感器网络节点的到达时间差实现对地下震源的定位。在使用无线传感器网络对地下震源进行定位时，巧妙地将地下震波在接收节点的计时延迟影响定位精度的误差，用差分误差抑制的方法消除。首先使用脉冲耦合时钟同步算法，同步所有节点时钟，随之测得震源到各个传感器网络节点的TDOA，建立相应目标函数，并采用遗传算法与拟牛顿算法各自的优势对目标函数进行快速求解。

本文仅采用4个传感器组成的网络即可对目标进行精确定位，而已有结果如WANG R H等[13]需要8个传感器才能解决定位问题。另外，遗传-拟牛顿混合算法实现了遗传算法的全局寻优和拟牛顿算法的快速局部寻优能力的有机结合，从而使得TDOA定位算法精度高、收敛速度快、稳定性高。

1 同步和定位算法

1.1 无线传感器网络脉冲耦合时钟同步算法

无线传感器网络脉冲耦合时钟同步算法的最初思想在WANG Y等[14-15]的研究中得以呈现。本文在其基础上进行调整，把传感器网络节点看作一个可以周期性地触发脉冲的振荡器。将相位变量xi与每个传感器节点(振荡器)i∈V相联系。脉冲耦合时钟同步算法如下：每个振荡器i∈V的脉冲相位以均匀频率ωi增加，当脉冲相位达到最大值2π时，振荡器发出一个脉冲并重置其相位为0。当振荡器接收脉冲时，利用耦合强度l∈(0，1)和相位值Q(xi)函数更新相位xi，称为相响应函数，即

(1)

由相响应函数可知，耦合强度l为相响应函数的斜率，在这个算法中，最佳的时钟同步是使用以下相响应函数，

(2)

由式(2)可知，给出不同时刻计时器的值即相位值xi，便可确定唯一的相位值Q(xi)。相位最大值xth=CL，CL是一个具有适当单位的任意值，一旦节点达到计时最大值，计时器溢出中断即相当于Mirollo模型[16]中的振荡器触发，同时向其他邻居节点广播触发信号，从而产生节点间的耦合效应。对所有接收到广播信号产生耦合效应的节点，本身计时器将进行清零处理(xi=0)，并重新开始计数，根据系统需求，可以步入下一个时钟同步周期。

1.2 TDOA定位方法

为便于阐述该定位方法的可行性与精确性，本文主要对二维平面内未知目标进行模拟定位，由二维的定位结论，可以扩展到三维及高维空间定位问题。设震源位置为(x，y)，(xi，yi)为第i个传感器节点的坐标，则震源与第i个节点的欧氏距离为

d(x，y)=‖x-y‖2。

(3)

本文先测得震源到各个节点的到达时间(TOA)，所发出的震源位于S∈R2中。如图1所示，震源发出一个球状的脉冲波。测得震波的TOA，起源于S，起始时刻为t0，在传感器pi处，位于径向距离r处的震源，有

(4)

式中：v为波速；ηi为误差。

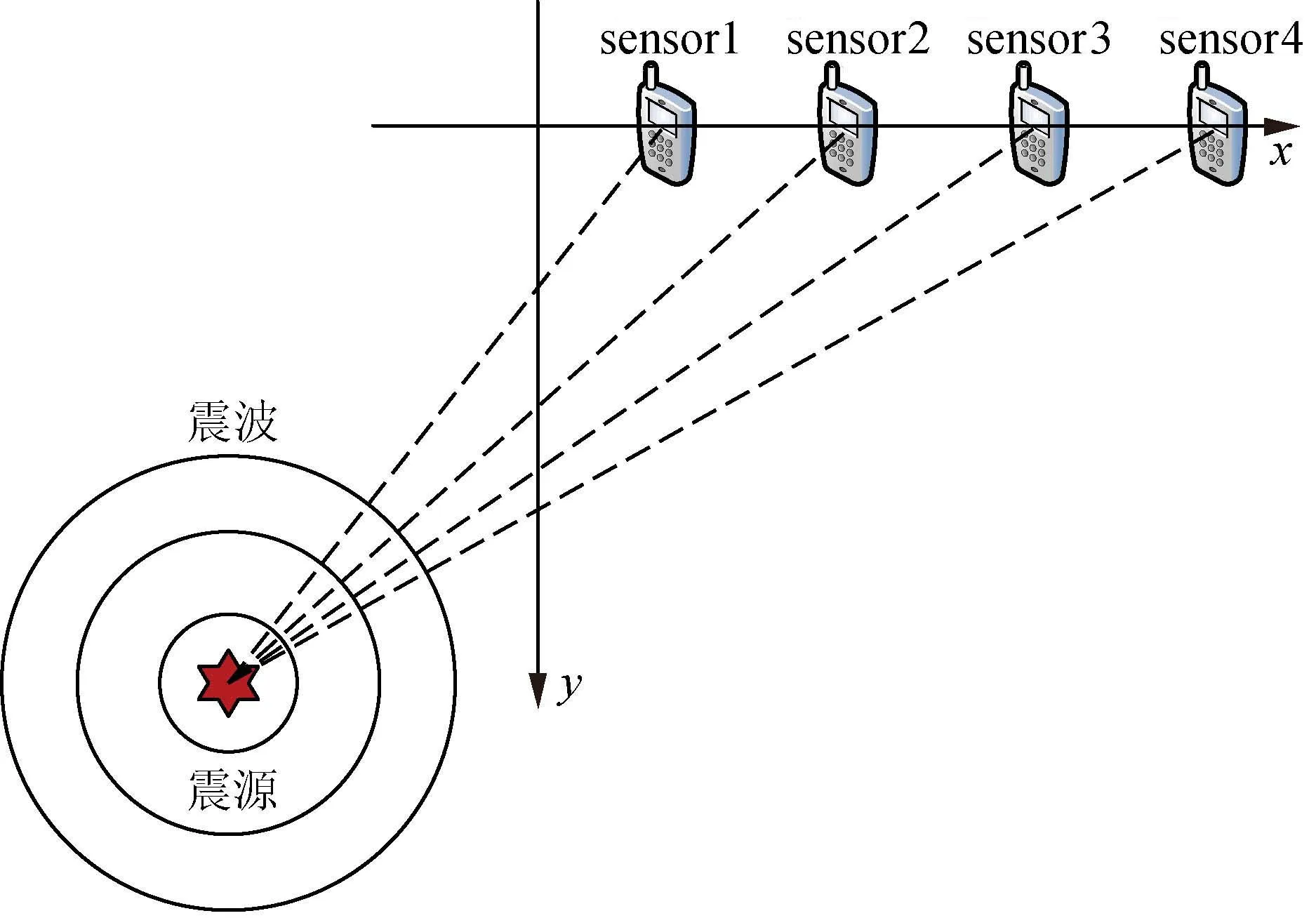
图1 震源定位模型

假设震波在均匀介质中传播。为了准确确定震源S的位置，一个传感器测量是不够的，因此，需要结合整个传感器网络进行综合定位。由于震源在某个未知时刻发出一段脉冲波，所以时间的起始量t0为未知，而且是一个额外的未知数，定位可以通过考虑传感器i和参考传感器rf∈V的TDOA进行计算，如式(5)所示。

TDOAi=TOAi-TOArf=

[d(S，pi)-d(S，prf)]/v+ηirf，

(5)

式中，ηirf为第i个节点与参考节点之间的误差。

把传感器p1作为参考节点，最大似然估计[17]震源的位置为

(6)

然而实际中由于测量和定位系统存在不可避免的误差，所以pi的位置不能精确确定。因此，式(6)得出的具体位置只能估计为

(7)

由式(7)可以设立所需目标函数，为

(8)

在传感器网络中，一个给定的传感器节点只需计数邻居节点Ni和收集TOA值，因此，各个节点之间的信息交换在传感器网络中起着至关重要的作用。基于式(7)，每一个传感器解决了本节点对震源的定位问题，然后与所有节点的定位结果相结合，最后平均化，获得一个精确位置。为了定位出未知震源的坐标，需要求解式(8)的解，即找到使式(8)最小的向量值(x，y)。本文选用遗传算法搜索出离精确解最近的坐标，将其作为拟牛顿算法的初始值，进行快速迭代，收敛至精确坐标，定位流程如图2所示。

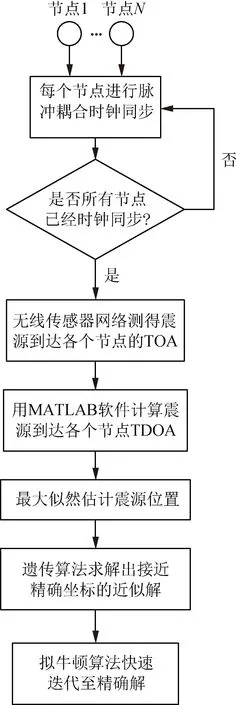
图2 定位流程图

2 混合算法

2.1 遗传算法

遗传算法(genetic algorithm，GA)是一种有效解决最优化问题的方法，通过快速搜索得到接近精确解的近似解。GA是模拟达尔文的自然选择和自然淘汰的生物进化过程的计算模型，也是近年来优化领域的研究热点。遗传算法具有全局搜索的功能，前期寻优搜索速度很快，因此，在解决很多复杂和状态多变的优化问题方面具有很大优势。本文将震源定位中的目标函数作为适应度函数，具体参数为：选用杂交概率Pc=0.7，变异概率Pm=0.15，学习率eta=0.8，最大迭代次数kmax=500。首先，需要给定搜索的空间范围和随机产生由400个个体组成的一个群体，GA以此400个个体为初始点开始迭代；其次，选择能够达到符合预期期望的适应度函数，即为本文的目标函数；最后。模拟种群随机交配原理，种群间进行选择、交叉和变异，产生子代，变异出新个体，进行自然选择，逐步选择适应新环境较强的个体，淘汰劣势个体，周而复始，直到满足所设迭代条件后，方可终止，具体算法流程见图3。

图3 遗传算法流程图

2.2 拟牛顿算法

拟牛顿法为牛顿法的改进，是属于局部收敛的算法[18]。遗传算法具有前期快速收敛寻优的功能，能够快速搜索到离精确值较近的近似解，而拟牛顿法正好利用了局部寻优的功能，将GA寻优的结果作为拟牛顿算法寻优的初始点，在局部区间(-200 m，200 m)内快速搜索。对于N维函数法f(x)在k处的泰勒级数展开，可以写为

f(x)=f(xk)+f(xk)(x-xk)+

(x-xk)T/22f(xk+1)(x-xk+1)+δ，

(9)

从此函数中可以发现，经过数次迭代，有可能会陷入局部极小值点，所以拟牛顿算法要求初始点离极值点不能太远，而遗传算法刚好弥补了此缺点。选择精度ε=1.0×10-25及最大迭代次数为1 000次，拟牛顿算法具体过程如表1所示。

2.3 遗传-拟牛顿混合算法

根据上面的讨论可知，拟牛顿算法容易陷入局部最优。因此，为了使拟牛顿算法获得全局最优解，必须求解问题的全局最优先验信息，这种要求过于苛刻，有时是不可能的。因此，将遗传算法的全局搜索能力嵌入到拟牛顿算法中，使拟牛顿算法不受初始搜索初值假定的约束，具体的流程如图4所示。

2.4 仿真与分析

对一个地下震源所产生的脉冲波进行定位，完全取决于震源瞬间产生的脉冲波。震源发出的脉冲波的起始时间显然未知，所以，基于TDOA的定位方法是合理的。如果采用较多的传感器节点,可以提高定位的精度，但是过多的传感器节点往往会增加成本和带来更多的干扰信号，所以为了在通信质量和定位精度之间达到良好的折衷，本文选用4个传感器组成传感器网络。新建传感器网络节点的坐标分别是(0 m，0 m)，(2 m，0 m)，(4 m，0 m)，(6 m，0 m)，波速v=230 m/s。在假定均匀介质中，波速传播速度一定，分别使用拟牛顿算法和遗传-拟牛顿混合算法对同一震源进行模拟定位，仿真模拟定位结果见图5～7。

表1 拟牛顿算法过程

图4 遗传-拟牛顿混合算法流程图

由图5拟牛顿算法x和y坐标的定位可知，经过30次左右迭代后，横坐标趋于稳定值为19.55 m，纵坐标为24.47 m，可得目标位置为(19.55 m，24.47 m)，其与标准值(20 m，25 m)误差约为3%。但是拟牛顿算法对初始值的要求比较高，如果初始值离精确值较近，则能快速收敛到精确值；如果初始值离精确值较远，则拟牛顿算法迭代求解的值很可能发散，无法得到精确解。

图5 拟牛顿算法横纵坐标迭代仿真

如图6～7所示，通过使用遗传-拟牛顿混合算法对未知震源坐标进行定位，充分融合了遗传算法和拟牛顿算法各自的优点，即利用遗传算法前期快速全局寻优的优点和拟牛顿算法后期局部迅速寻优的优点。由仿真图6可知，遗传-拟牛顿混合算法经过2次迭代就已经趋于稳定值：最后稳定值的横坐标为19.75 m，纵坐标为24.51 m，目标坐标(19.75 m，24.51 m)，与标准值(20 m，25 m)误差约为1.5%，精度得到大幅提升。产生此误差的原因是：计时器存在计时频率偏移、时钟时延和系统外部干扰信号。如图7所示，在寻优速度方面，遗传-拟牛顿混合算法远远优于拟牛顿算法。因此，对于地下震源的定位，综合比较拟牛顿算法和遗传-拟牛顿混合算法的收敛速度及精确度的优点，应选用遗传-拟牛顿混合算法对地下震源进行定位。

图6 遗传-拟牛顿混合算法横纵坐标迭代仿真图

3 结 语

为了提高无线传感器网络的定位精度及效率，提出一种基于遗传-拟牛顿混合算法的到达时间差定位方法，因为地下震源的起始时间未知且无法实际测量，所以提出到达时间差的定位方法更具优势。假定波速在均匀介质的条件下传播，建立目标函数，通过遗传-拟牛顿混合算法进行求解。前期用遗传算法进行全局快速寻优，搜索出离精确值较近的坐标，然后将其作为拟牛顿算法的初始点，再进行局部寻优，最终能够搜寻出比较逼近真实值的坐标，并分析了理论上的误差。由仿真结果可知，本文所选基于遗传-拟牛顿混合算法的TDOA定位方法精度较高，且遗传-拟牛顿混合算法比拟牛顿算法定位算法收敛速度快、定位稳定性好。