关于机械能守恒定律是否满足相对性原理的探讨

杨习志 赵 坚

(1. 昆明市第一中学，云南 昆明 650031； 2. 昆明市五华区基础教育科学研究中心，云南 昆明 650031)

笔者发现关于机械能守恒定律是否满足相对性原理的争论，[1～7]其核心问题主要来自于3个方面.其一，讨论问题中系统的机械能作为物理量所涉及的守恒是否满足相对性原理，是否是协变的？其二，机械能守恒定律作为一条物理定律是否满足相对性原理，是否是协变的？其三，系统的机械能不具有独立协变性是否与相对性原理矛盾？为此，笔者分别从这3个角度出发进行探讨.

1 系统的机械能是守恒量吗？

在分析力学里，对于力学量

w=w(qα,pα,t).

判断其守恒的充要条件是

其中qα、pα、t为力学量w的广义坐标、广义动量和时间，

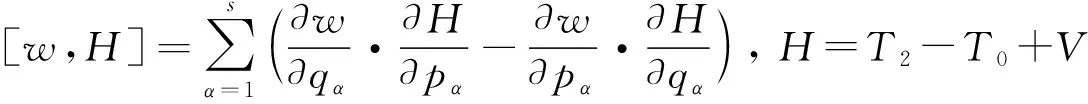
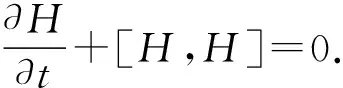
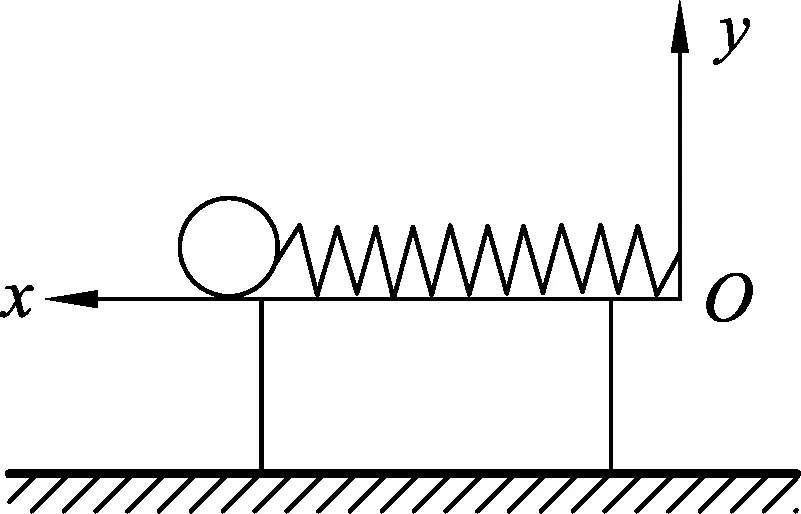
图1

如图1所示，在光滑的水平桌面上有一个质量为m的小球与一根轻质弹簧连接，弹簧的右端固定在O点，劲度系数为k,原长为x0,则小球与弹簧整个系统广义能量的哈密顿量：

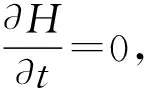
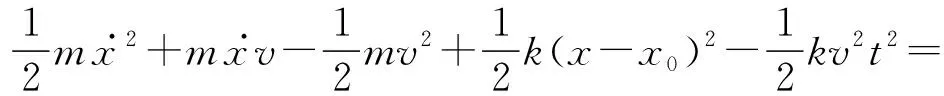
从式中可以看出经过坐标变换后的哈密顿量H′是显含时间的,即

故变换后系统的机械能不守恒．同理,若在y方向上运动的惯性参考系来进行观测,经过坐标变换后,会发现变换后系统的机械能仍然守恒,可见系统的机械能不是一个普遍的守恒量,它会随参考系的改变而改变．究其原因,通过前面的讨论会发现主要是因为机械能的哈密顿量中势能V是位置的函数,而位置坐标在进行该方向上的坐标变换时会携带时间,导致机械能的哈密顿量H对时间的偏导数不为0．同理可得系统动量的哈密顿量与位置坐标无关,在经过坐标变换后的哈密顿量仍然不显含时间,故系统的动量是一个守恒量．

我们也可从机械能守恒的条件出发来进一步分析.根据功能原理,机械能守恒的条件是外力与内非保守力做功为0,其中内力做功

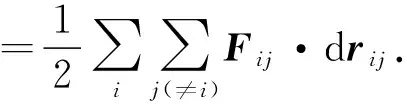
根据坐标变换有

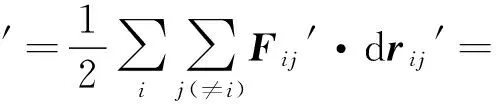
故内力做功与参考系无关,其中内力又分为保守内力和非保守内力,保守内力做功等于系统相互作用的势能的减少量,非保守内力则会改变系统的机械能,如摩擦生热或爆炸．

对于外力做功

dw外=∑Fi·dri.

根据坐标变换有

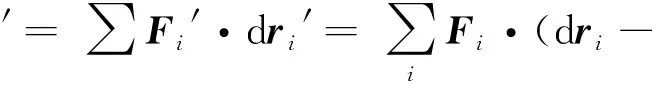
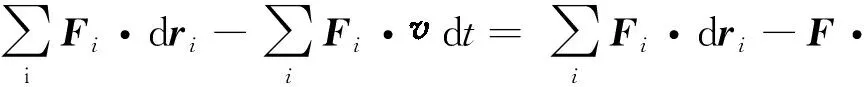
可见,由于外力做功与参考系有关,不满足协变性,从而导致机械能守恒的条件在经过坐标变换后得不到满足．故系统的机械能作为物理量而言是不满足协变性的,它不是一个守恒量．反观动量守恒问题,由于系统动量守恒的条件是合外力为零,而合外力是不会随惯性参考系的选取而变的,即在一个惯性参考系中系统所受的合外力为零,那么在另一个惯性参考系中系统所受到的合外力仍然为0,故系统动量守恒的条件满足协变性,系统的动量是一个守恒量．

2 系统的机械能不具有独立协变性是否与相对性原理矛盾?

2.1 相对性原理表述之联立协变

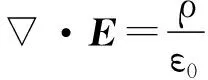
2.2 机械能守恒定律与协变集

如果自然界若干定律联立在一起,进行参考系变换,然后再在新参考系中对变换结果进行等价变形,可化为具有原来形式的全部新定律,则这些定律称为是联立协变的.这些定律作为元素所构成的集合称为协变集,其中,只含有一个元素的协变集称为单元素协变集,元素不能再减少的协变集称为最小协变集．如麦克斯韦方程组中的高斯定理与修正的安培定律,法拉第电磁感应定律与高斯磁定律分别构成两个四元素最小协变集,电荷守恒定律构成单元素最小协变集,机械能守恒定律则属于功能原理的最小协变集．

3 机械能守恒与功能原理联立协变

功能原理即

dw=dw内+dw外=dw内保+dw内非保+dw外保+dw外非保=-(dEp内+dEp外)+dw内非保+dw外非保=-dEp+dw非保=dEk.

dw非保=dEp+dEk，

当dw非保=0时,dEp+dEk=0，

即Ep+Ek=C.

故机械能守恒是功能原理的特殊情况,但由于条件dw非保=dw内非保+dw外非保中的dw外非保与参考系有关,故机械能守恒的条件是与参考系的选取有关的．值得注意的是,根据坐标变换有

dw外′=dw外-F·udt，

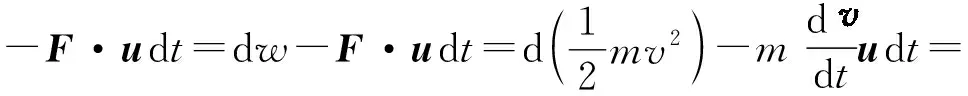
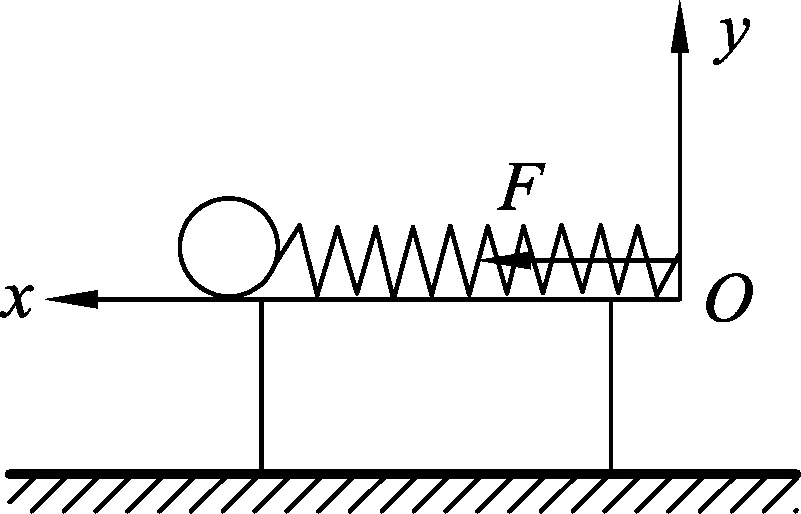
图2

可见功能原理满足相对性原理,是协变的．其次,由于机械能守恒是功能原理的特殊情况,故机械能守恒是功能原理的最小协变集,与功能原理联立协变．下面从功能原理出发,重新探讨在x方向上以u向右运动的惯性参考系中来观测图1中系统的机械能,假设弹簧此时处于压缩状态,且小球正在向右运动,则小球和弹簧整个系统将受到墙壁对它向左的推力F的作用,故有

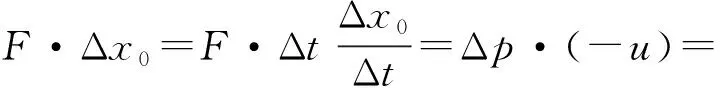
-mu(v2-v1).

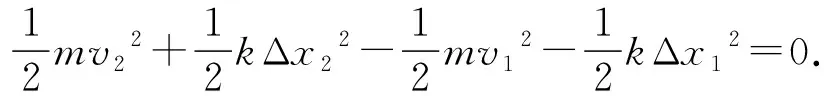
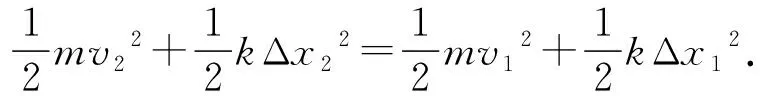
可见,从功能原理出发,可以得出与地面为参考系下相同的机械能的表达形式,因此,机械能守恒与功能原理是联立协变的．

4 守恒量与守恒定律

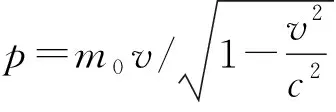
鉴于此,我们可以这样认为,机械能守恒定律是能的守恒和转化定律(功能原理)在力学中的一种特例．作为自然界最普遍的物理规律之一的能的守恒和转化定律,一定是满足相对性原理,是协变性的,但是加上一些不协变的条件(初始条件、边界条件、规范条件等),就不协变了,因为,能量守恒定律的普遍表述是“一个系统能量的变化等于非保守外力做功”.这句话不能理解为“能量不变(守恒)”,能量不变(守恒)涉及3个问题: (1) 系统的选择,(2) 什么是保守力?(3) 做功的条件,而我们只有对选定的系统才能区分内力和外力．我们通常说保守力做功与路径无关,是指沿路径的积分是“等时”的,没有移动时间的概念,同时,保守力一定是个势力场,而只有不含时间的力场才能保证能量不变,否则能量必然变化．所以,一切普遍规律(微分方程)都是协变的,此点无容置疑,可是,系统的机械能守恒在满足相对性原理,是否具备单独协变性的问题上,是有条件的,它只能与功能原理联立协变．

综上所述可以看出,机械能守恒定律作为物理定律在守恒条件满足的情况下在任意惯性系下均具有相同的表达形式,满足相对性原理,是协变性的．但系统的机械能作为物理量来说本身并不是一个守恒量,其根本原因在于机械能的哈密顿量中势能是位置坐标的函数,在进行该位置坐标上的坐标变换时总会携带时间,导致其哈密顿量对时间的偏导数不为0,也可理解为外力做功与参考系有关导致机械能守恒的条件随参考系的选取而变,使得系统的机械能不满足相关坐标变换,此时,系统的机械能只能与功能原理联立协变．

(致谢:本文曾得到北京大学赵凯华先生的悉心指导,借此深表感谢!)