探究卫星沿椭圆轨道运动的两个有趣问题

郑 金

(凌源市职教中心，辽宁 朝阳 122500)

在贵刊2014年第7期发表的《为什么发射速度越大线速度越小》一文中，应用机械能守恒定律和引力势能公式定量推导了卫星做匀速圆周运动的线速度与发射速度的数量关系；利用离心现象理论说明了卫星沿椭圆轨道运动到某一位置时改变卫星运动方向可做圆周运动，此时万有引力恰好等于所需的向心力.不仅解答了疑难问题，而且提供了解题的两条途径，即从能量观点和动力学观点分别进行解析，但没有明确得出卫星沿椭圆轨道运动到何处变轨才能恰好做圆周运动.再者，只论证了卫星做圆周运动的线速度随高度变化的关系，而没有论证卫星沿椭圆轨道运动到远地点时的速度如何随高度变化的关系.下面应用机械能守恒定律和天体椭圆运动的机械能公式对这两方面问题进行举例分析.

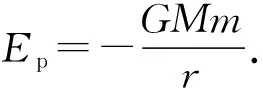
对于在半长轴为a的椭圆轨道上运行的卫星，在从近地点运动到远地点的过程中机械能守恒，即

由角动量守恒定律有mv1r1=mv2r2，联立方程可得卫星在远地点时的动能为

可知卫星的机械能为

可见，沿椭圆轨道运动卫星的机械能公式跟沿圆周轨道运动卫星的机械能公式很相似，而且都为负值.

1 卫星在椭圆轨道何处变轨才能做圆周运动

当卫星沿椭圆轨道运行到顶点时，只有当发动机提供动力突然加速时才能沿切线方向做圆周运动.另一种情况是，当卫星沿椭圆轨道运行到某高度处时保持速率不变而改变运行方向，使卫星受到的万有引力恰好等于所需的向心力而做匀速圆周运动.那么当卫星运动到离地面的高度为多大时，或者说卫星在椭圆轨道何处变轨时，才能恰好做圆周运动呢？为了回答这个问题，可通过一道例题来分析说明.

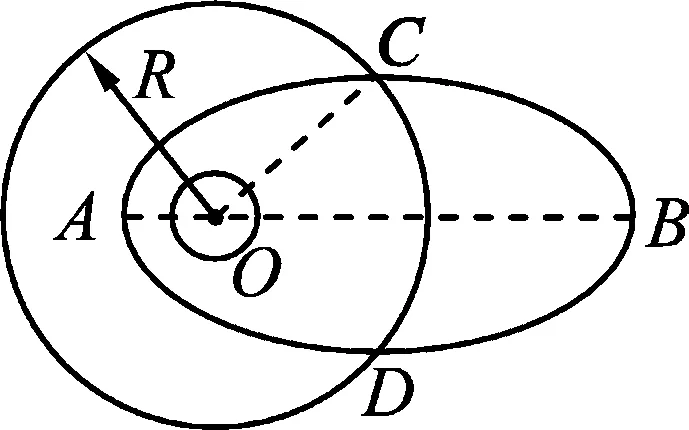
图1

例1.如图1所示，两颗质量相等的人造卫星分别在圆轨道和椭圆轨道上绕地球运动，两轨道和地心O在同一平面内，轨道的交点为C、D.已知椭圆轨道的半长轴为a，如果两颗卫星先后运动到轨道交点C时的速率相等，那么轨道交点到地心的距离为多少？

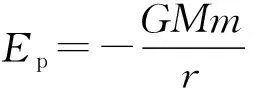
由椭圆的定义可知短轴端点到焦点的距离等于半长轴，而图1中的圆周半径OC恰好等于椭圆的半长轴，因此交点C是椭圆短轴的端点，所以两个交点平分椭圆轨道.有趣的是，只要圆周半径恰好等于椭圆的半长轴，两颗卫星运动的周期就相等，这与开普勒第三定律是一致的.

综上可知，对于沿椭圆轨道运行的卫星，只要变轨位置在椭圆短轴的端点，或者说到地心的距离等于椭圆的半长轴，且在此处保持卫星的速率不变，仅改变速度方向，使速度垂直于此处与地心的连线，那么卫星即可绕地心做匀速圆周运动.若卫星在同一近地点的速度越大，则椭圆的半长轴就越长，那么使卫星恰好能做圆周运动而变轨的位置就越高，对应的圆周半径就越大，在此处的速度就越小.

2 卫星在远地点的速度如何随椭圆长轴而变化

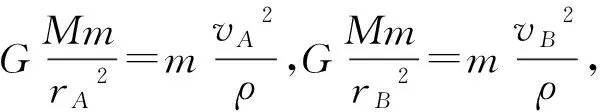
如果卫星在近地点时被发动机加速，变轨到更高的椭圆轨道，那么到达远地点时的速度也增大吗？或者说，如果卫星分别沿两个相切于近地点的椭圆轨道运动，那么到达远地点时的速度哪个较大？下面进行举例说明.

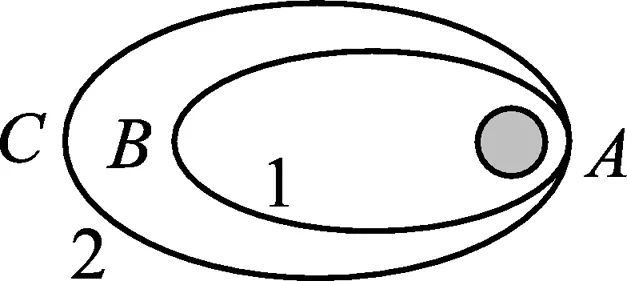
图2

例2.如图2所示，两颗质量相同的卫星运行的椭圆轨道在同一平面内相切于同一近地点A，这相当于同一卫星在近地点的发射速率不同，沿不同的椭圆轨道运动.设地球的质量为M，半径为R，卫星在近地点时到地面的距离为h，试求： (1) 卫星在不同远地点时的机械能总量哪个较大？(2) 卫星在不同远地点时的速度哪个较大？

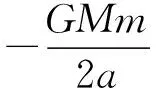
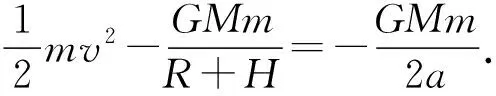
椭圆的长轴为2a=H+2R+h，所以

由于椭圆轨道1的长轴较小，因此卫星在远地点时的速度较大.

式中只含有一个未知量a，由此可见，若椭圆轨道半长轴的长度越大，则卫星在远地点时的速度就越小.对于沿椭圆轨道运行的卫星，若在同一近地点时的速度越大，则在远地点时的高度就越大，那么在远地点时的速度就越小.

从解题过程可见，在应用机械能守恒定律解答有关以地心为焦点的椭圆运动问题时，可直接利用地球卫星做圆周运动的机械能公式和天体沿椭圆运动的机械能公式列方程.这种方法在解答物理竞赛题时应用比较广泛，而且能化繁为简.