基于同化竞争QPSO算法的结构模态参数识别

孟 浩，卢俊龙

（1.江苏合谷建筑设计有限公司，江苏 苏州215000；2.西安理工大学 土木建筑工程学院，陕西 西安710048）

当前我国城市化进程不断加快，建成了规模较大的高层建筑及大跨度桥梁。而随着时间的推移，工程结构在材料的老化、环境侵蚀、超载工作和灾害等因素的作用下，出现强度及刚度退化，严重影响结构使用功能。因此，利用现代信息及计算机分析方法等，对服役结构进行健康检测和损伤识别，实时监控结构安全情况，预防各类灾害的发生。

当前，许多研究人员将自动计算技术与结构参数识别相结合，提出了效率更高的优化识别方法。Perry和Koh[1]等人对遗传算法进行改进，并进行结构参数识别；Koh[2]等人利用遗传算法对剪切变形结构进行整体参数识别，效果较好；Tang[3]将微分演化算法引入系统识别中，群体智能优化算法是目前应用较为流行的一种算法，在计算机、经济及结构工程等领域得到大量的应用。PSO算法凭借概念简单、容易且收敛速度快，已在很多领域得到应用。Coelho和Krohling等人[4]在结构整体识别当中，引入PSO算法，取得了较好的分析结果。榎本裕里[5]将PSO算法进行优化，将其中系统识别问题转化成高维多模优化问题，并进行了相关分析。张伟[6]将标准的PSO算法引入结构参数识别当中。虽然，PSO算法得到了大量应用，但依然存在容易陷入局部最优的问题。针对这一情况，孙俊等人对其进行改进，提出了量子粒子群算法（QPSO）[7]，同样，在模态参数识别领域，王兰彬[8]将QPSO算法运用到结构模态参数识别当中，取得了较好结果。常军[9-10]采用频响函数作为目标函数，运用QPSO算法，对环境激励下的结构模态参数进行了有效识别，效果较好。闫天红等[11]根据结构振动特征方程，分析了结构模态参数对结构参数改变的灵敏度表达式，建立了结构模态参数损伤识别关系式。方圣恩等[12]对于结构不确定性损伤识别问题进行了研究，发现经典区间算法容易发生扩张。虽然，QPSO为一种优化后的算法，但是，也存在全局寻优速率不足的问题，特别当应用在结构参数识别中时，由于优化问题比较复杂，所以识别精度仍不是很高，且常常不容易收敛，或陷入局部最优。针对QPSO算法全局寻优效率较低的，易陷入局部最优的问题，本文对QPSO算法进行优化，并通过测试函数来验证其有效性。通过简支梁与振动台试验分析，表明该方法具有较好的模态识别能力，可靠性较高。

1 基于同化竞争QPSO算法

1.1 同化竞争方法

本文将同化竞争方法引入量子粒子群优化算法（ACQPSO）当中，根据QPSO算法，每次迭代产生一个全局最优粒子，并不断影响其余粒子，使其与自己越来越接近。以数学方法对同化过程进行表示，采用随机数y表示粒子与全局最优粒子之间的移动的距离，具体公式为

式中，ξ为同化系数，d为粒子与全局最优粒子之间的距离。得到粒子移动公式为

式中，Xnew为同化后粒子新位置，Xold为同化前位置，V为方向向量。

同化可以看成是粒子向最优值的进一步发展，在最优粒子同化的同时，粒子与粒子之间也产生斗争，在这也可理解成是一种竞争关系，粒子之间互相竞争，若存在更优的粒子，这个粒子将取代原来的最优粒子，其粒子运动示意图如图1所示。总的来说，在QPSO算法的粒子进化方式中引入同化与竞争思想，能有效提高全局寻优效率，并改善算法容易陷入局部最优的缺陷。

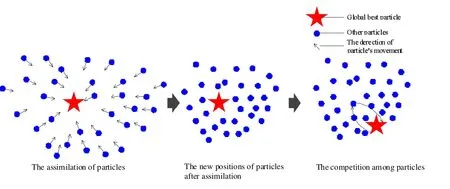
图1 粒子同化与竞争示意图

1.2 改进算法有效性分析

针对ACQPSO算法的有效性进行验证，对6个常用标准测试函数进行分析，函数相关信息如表1所示，采用ACQPSO算法进行识别，并与QPSO计算结果进行比较。在这次分析当中，种群规模、维数、最大迭代次数分别为：20、10和1 000，收缩-扩张因子α的值随迭代次数从1.0到0.5线性减小，同化系数ξ=2。具体结果见表2。

表1 测试函数相关信息

表2 测试函数的测试结果

对计算结果和寻优曲线分析发现：ACQPSO的计算效果远远好于QPSO算法，说明同化和竞争的引入，可大大提高粒子进化过程，明显增大算法的寻优效率、收敛速度，降低陷入局部最优的概率，取得了令人满意的结果，见图2。

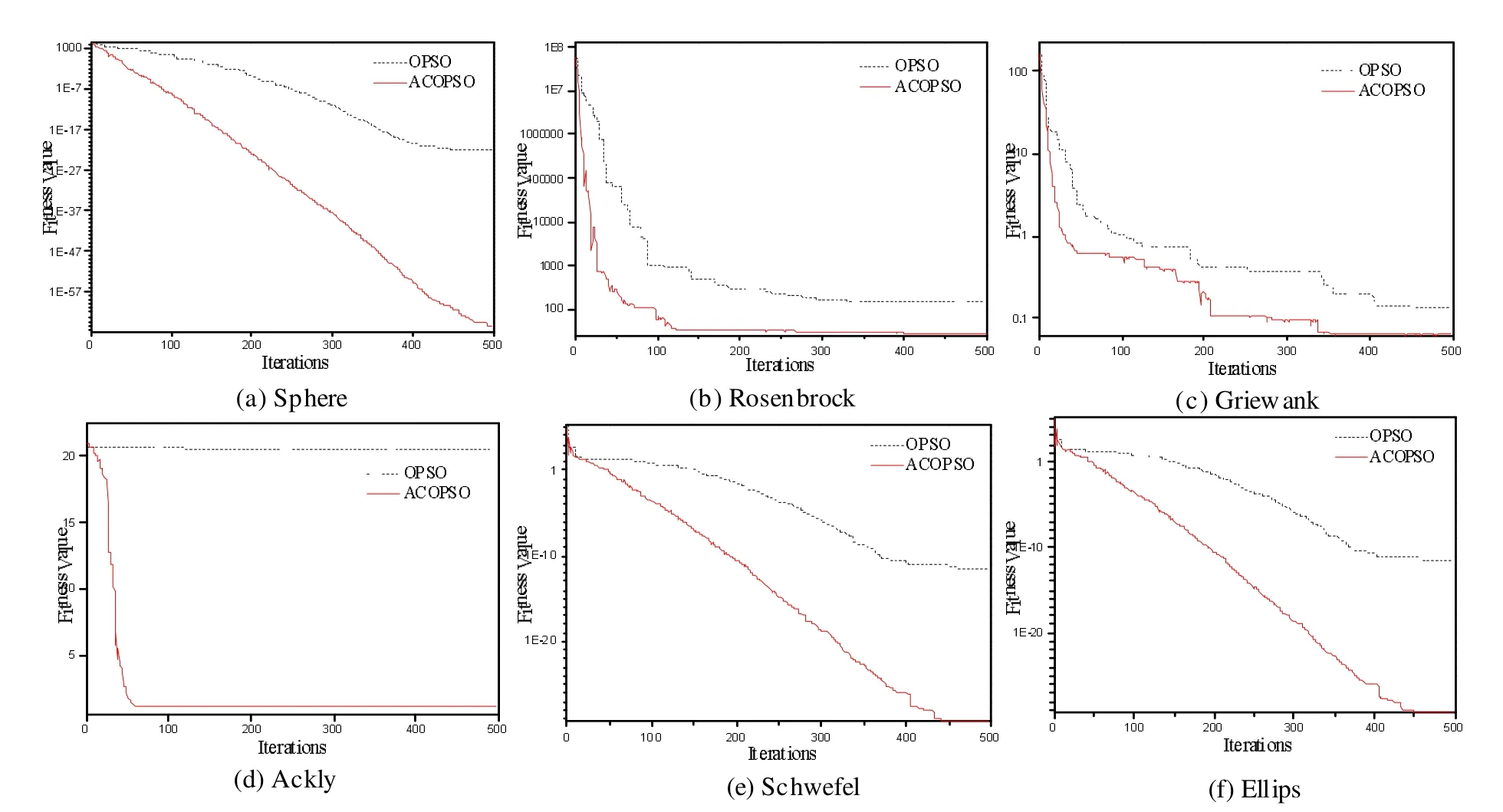
图2 寻优曲线变化规律

2 模态参数识别方法

2.1 问题描述

模态参数识别的关键在于缩小结构实际响应与预测响应之间的误差。设y（t）为k个自由度粘性阻尼结构的振动响应，具体公式为

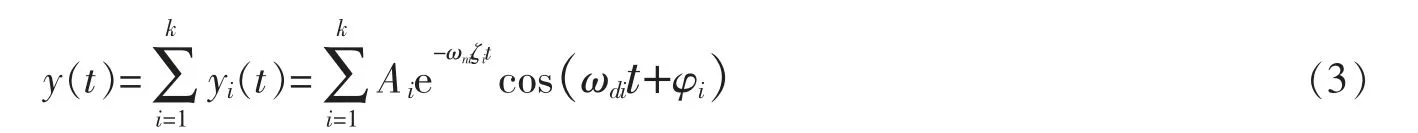
式中，yi（t）为振动响应输出，Ai为振动幅值，ωni为无阻尼圆频率、ωdi为有阻尼圆频率，ζi为阻尼比，φi为相位角，t为时间。有阻尼圆频率ωdi计算公式为

区内地势较为平缓，海拔在2800～3700m，最高山峰位于滩北雪峰东北的黑山，海拔3983m，相对高差较小，多在50～200m之间。区内的地貌主要由山体、剥蚀残山和河谷型小断陷盆地构成。在地貌分类学上属于剥蚀平原、丘陵、低山地貌类型，平缓地区多为可移动的沙丘。区内的山体多为长条带状NWW向展布，山体宽数百米至数千米。

均方误差函数计算公式为

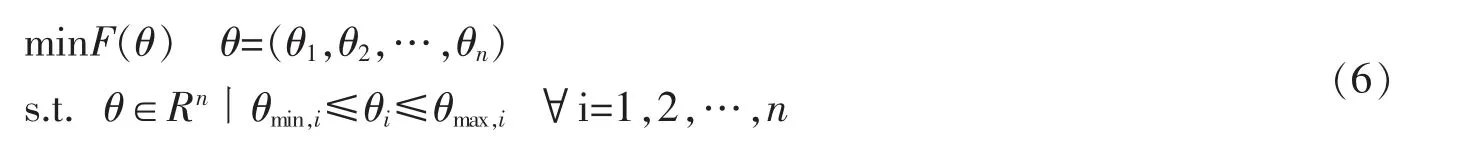
式中，θmax、θmin分别表示识别参数区间上、下界。

2.2 识别步骤

本文将运用ACQPSO算法作为优化算法，对结构模态进行分析识别，具体流程：

（1）根据结构模态参数，确定需要识别的维数；再按照待识别的参数，进行可行解空间大小的判断；

（2）根据结构激励的输出信号，基于待测模型的均方误差建立目标函数；

（3）根据ACQPSO方法，对上面的目标函数进行优化；

（4）给出终止条件，以此对全局最优位置进行判断。

其计算流程见图3。

3 结构模态参数识别应用与分析

3.1 简支梁数值模拟

简支梁模型及加速度传感器布置情况如图4所示，为两端简支矩形梁，具体尺寸为26 mm×10 mm，梁长为3 m，采用Q235钢制作。在加速度传感器位置进行白噪声扫描。采样频率为1 000 Hz，响应信号时间50 s，按要求设置Rayleigh阻尼，加噪0%，5%，10%，20%，30%。模型分析分别采用QPSO和ACQPSO算法，进行结构模态参数识别，粒子数为60，迭代数选用2 000，α随迭代次数从1.0到0.5线性减小，同化系数ξ=1.5，分析结果如表3至表5所列。

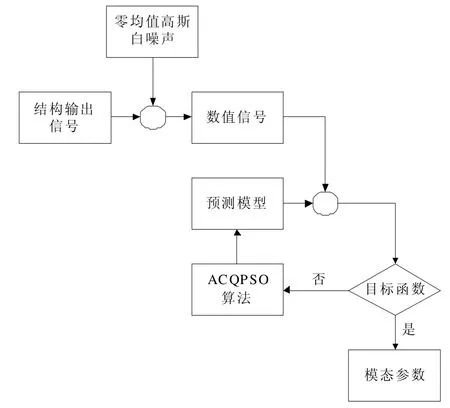
图3 基于ACQPSO算法的模态参数识别

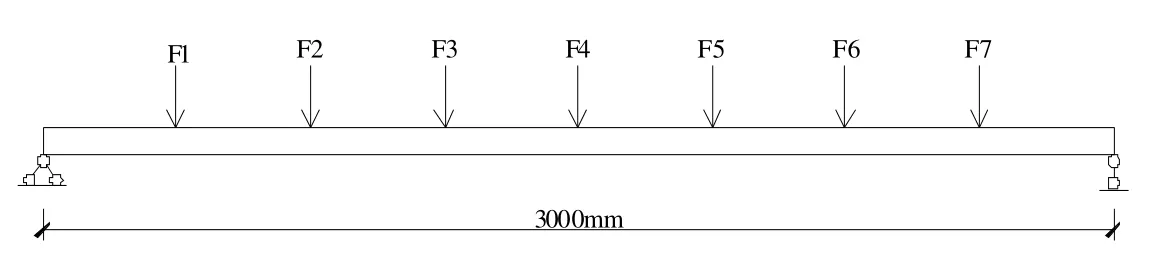
图4 简支梁模型

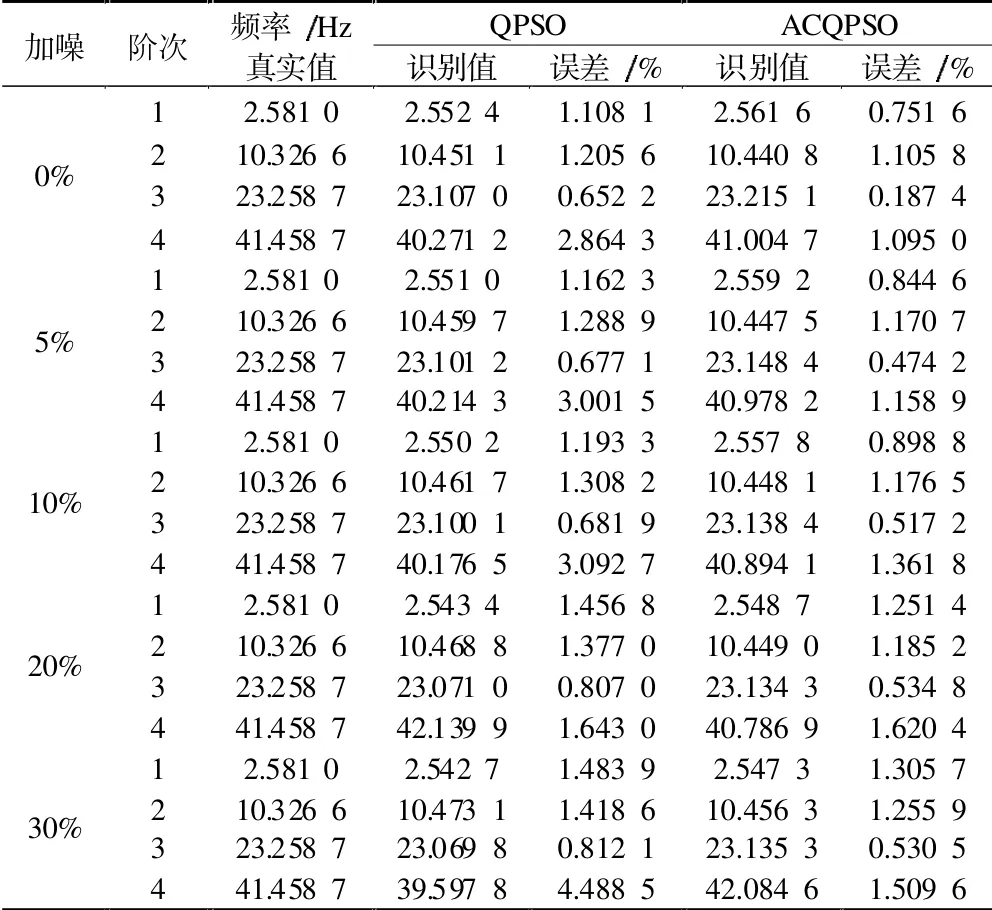
表3 结构固有频率分析

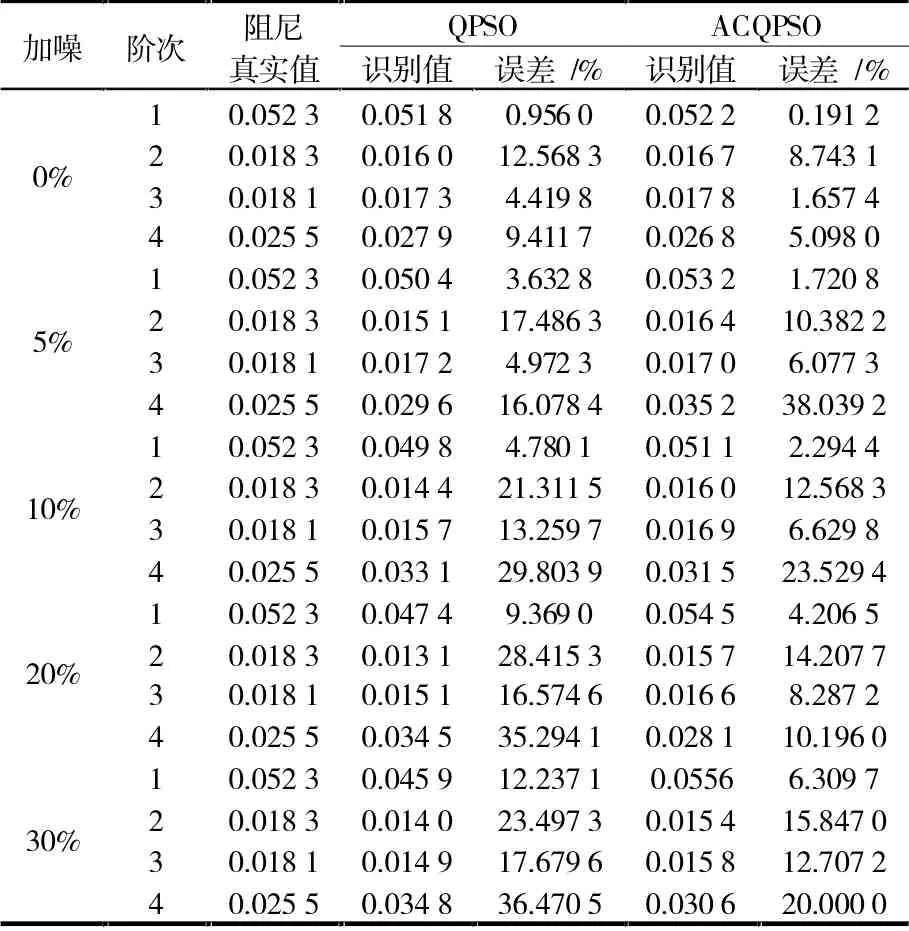
表4 结构阻尼比识别结果

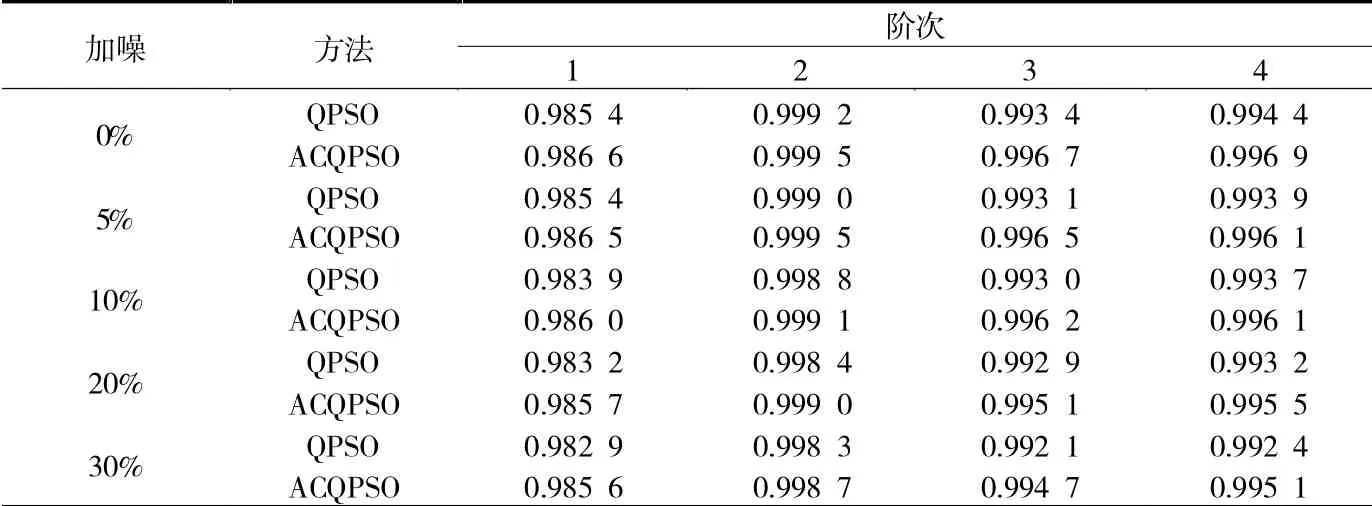
表5 结构振型MAC值识别结果

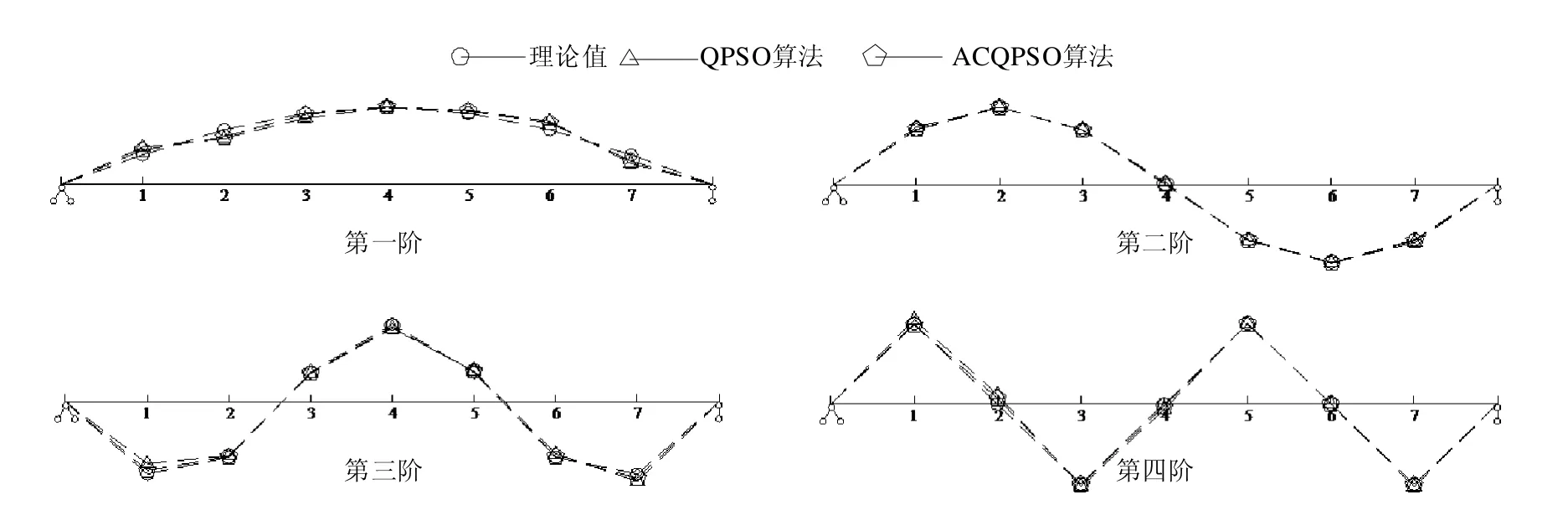
图5 0%噪声下的简支梁结构振型识别

通过对简支梁模态识别结果进行分析，可以发现：均方误差作为目标函数，可有效识别结构模态参数，频率、阻尼、振型等识别结果均较为精确。对比分析QPSO和ACQPSO可发现，后者明显占优，特别在频率和振型的识别方面。随着噪声不断提高，ACQPSO算法的抗干扰能力也更好。

3.2 三层框架结构参数识别

针对如图6所示3层钢框架进行振动测试，每层布置有加速度传感器，用来分析各层加速度响应，传感器采样频率为512 Hz，以试验开始作为0 s时刻，第5.85秒时开始激励，第20秒试验结束。收集提取全部试验数据进行分析处理。分别采用峰值法、QPSO和ACQPSO算法，对信号响应进行处理分析。试验识别粒子数为60，迭代次数是3 000，α的值随迭代次数从1.0到0.5线性减小，同化系数ξ=1.5，识别结果见表6和表7。

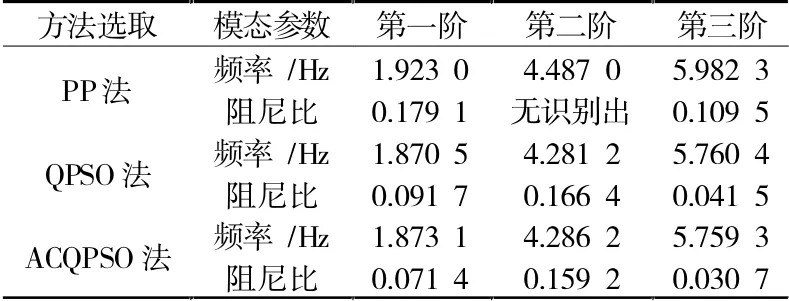
表6 结构频率及阻尼识别

图6 三层框架结构试验

由于PP法在识别方法中较为成熟，本文采用PP法的识别结果作为对比标准，来检验ACQPSO算法的有效性，见图7。从试验识别结果来看，频率方面，ACQPSO与QPSO算法的识别结果与PP法都较为接近；阻尼方面，PP法对于结构第2阶阻尼数值识别较差，而QPSO与ACQPSO识别结果较为准确；振型方面，通过MAC值对比，ACQPSO算法与PP法识别结果较为接近。由此可见，ACQPSO算法具有较高精度与可靠性。

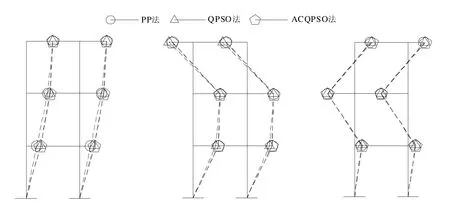
图7 三层框架试验振型识别

4 结语

由于QPSO算法全局寻优效率较低，易陷入局部最优问题，本文采用同化竞争方式进行优化，提出ACQPSO算法。针对几种典型测试函数进行分析发现，该算法的全局寻优效率得到明显提高，同时，避免了陷入局部最优的问题。采用ACQPSO算法对简支梁进行识别分析，计算结果显著优于QPSO算法，表明优化后的识别精度与抗干扰能力都得到加强。对三层框架结构进行振动测试，分析动态信号，并采用PP法作为标准，结果发现：ACQPSO无论从识别精度，还是抗干扰性上，都具有显著的优势。