集群无人机队形重构及虚拟仿真验证

卢燕梅，宗群，张秀云，鲁瀚辰，张睿隆

天津大学 电气自动化与信息工程学院，天津 300072

四旋翼无人机具有成本较低、设备简单、飞行灵活等特点，近些年来广泛应用于军事和民用领域，如目标侦察、应急救援、农业植保、无人机灯光表演等。随着任务复杂度的增加，单架无人机往往难以满足任务需求，因此无人机集群控制及其应用由此成为当下的一个研究热点，多无人机集群能够提高执行任务的效率、灵活性和容错能力。无人机编队队形控制方法是实现多无人机编队安全飞行的前提和必要手段[1]，其中集群无人机队形重构是集群无人机所要考虑的一个重要问题，主要是一定数量的无人机根据特定要求变换队形，需要研究无人机路径规划算法和轨迹姿态控制算法等。

对于集群无人机队形重构的路径规划，主要目标是让每架无人机都能从初始位置无碰撞地到达最终位置，保证队形重构过程中代价最小或能耗最优[2]。这其中既包含目标分配问题，即每架无人机被分配到的目标队形的某一特定位置；又包含轨迹生成问题，保证无碰撞地到达目标位置。许多算法对上述两个问题进行了解耦，即先进行目标分配，分配好目标位置之后再进行起始点到分配好的目标位置之间的轨迹生成，其中目标分配问题多利用匈牙利算法[3]进行解决。分配好目标位置之后，在轨迹生成部分，常见算法包括图搜索算法A*[4]及其变体[5]、自适应随机搜索算法[6]、模型预测控制[7]、混合整数规划[8-9]等。以上算法在单一无人机规划时效果较好，但是在多无人机轨迹规划时普遍存在计算难度加大、规划时间增长、规划效率难以满足实际应用时的实时性要求等缺点，因此，需要探索计算简便、效率高的多无人机路径规划算法。

在无人机集群由同构无人机构成的情况下，每个目标可以任意分配给各架无人机，则称之为无标号问题。若集群中包含异构无人机或某些特定情境下针对某一目标位置只能被分配给特定无人机(如快递运输)，则称之为带标号问题。Kumar等针对无标号问题提出了许多算法，其中CAPT(Concurrent Assignment and Planning of Trajectories)算法[10]对多架无人机进行并行的目标分配和轨迹规划。考虑到将目标分配和轨迹生成问题解耦计算的问题复杂度，该算法将上述2个问题耦合，提出了包括集中式CAPT(C-CAPT)和分布式CAPT(D-CAPT)2种实现思路，实现了无障碍物情况下的多机无碰撞全局路径规划，极大降低了计算的复杂程度，提高了实时性和实用性。随后Kumar团队的Tang等基于带标号问题，在CAPT算法的基础上相继提出了OMP+CHOP(Optimal Motion Plans+ Circular HOlding Patterns)算法[11]、HOOP(HOld or take Optimal Plan)算法[12]，针对无障碍的拥挤环境，提出在无碰撞时采取CAPT算法、将要碰撞时采取圆形保持轨道进行轨迹设计的思路，扩展了CAPT算法的研究情景和研究领域。

对于无人机队形重构的控制问题，主要目标是控制无人机追踪预设轨迹，保证在一定外界干扰的情况下仍不发生偏移。若干扰有界，滑模控制算法在四旋翼无人机控制中应用广泛[13]，在文献[14]中研究了一种终端滑模控制算法，可以很容易地消除飞行中扰动影响，但是主要缺点是控制律不连续引起的抖振。高阶滑模控制算法如螺旋和超螺旋滑模控制可以产生连续控制信号，抵消连续扰动，文献[15]利用内-外环结构设计了一种超螺旋滑模控制器。文献[16]则提出了利用连续律来控制无人机姿态的新策略，但前提条件必须是扰动边界已知。文献[17]提出了一种新的连续多变量积分滑模控制器。结合连续标称控制器和改进的超螺旋控制器来实现对干扰的有效抑制。基于扰动上界未知问题，引入自适应控制算法，文献[18]设计了一种自适应终端滑模控制策略，实现了有限时间收敛。文献[19]提出的自适应终端滑模有限时间控制算法能有效满足姿态跟踪控制的快速性需求。无人机控制算法大多针对单输入单输出系统进行设计，文献[20]设计多变量有限时间积分滑模控制器，保证了对期望参考输入的高精度快速跟踪控制。采用多变量控制算法可以避免对多输入多输出系统设计时进行解耦[21]，从而一定程度上提高控制效果如减少滑模控制算法的抖振现象。

本文考虑集群无人机队形重构问题，首先基于四旋翼无人机轨迹姿态数学模型，利用CAPT算法进行集群无人机路径规划，实现对多无人机的并行位置分配和最优轨迹生成；其次，分别考虑干扰影响下的无人机轨迹及姿态控制系统，提出姿态解算及新型连续多变量积分滑模控制器设计算法，实现对无人机轨迹的有限时间精确跟踪；最后，搭建Gazebo-ROS无人机仿真平台，在该平台下实现了12架四旋翼无人机队形重构过程的整体效果仿真，验证所提算法的有效性和实用性。

1 四旋翼无人机轨迹姿态模型

本文所采用的四旋翼无人机模型示意图如图1所示。xB、yB、zB为无人机机体坐标系，xW、yW、zW为无人机惯性坐标系。Fi(i=1,2,3,4)及Mi(i=1,2,3,4)分别代表4个电机产生的升力及力矩。充分考虑四旋翼无人机的固有特性，无人机在飞行过程中的动力学因素及受力平衡关系，其轨迹姿态数学模型为[22]

(1)

(2)

(3)

(4)

式中：p=[x,y,z]T∈R3，v=[vx,vy,vz]T∈R3，Θ=[φ,θ,ψ]T∈R3分别为无人机惯性坐标系下的位置、速度和欧拉角；Ω=[ωx,ωy,ωz]T∈R3表示机体坐标系下的姿态角速率；g=9.8 m/s2为地球重力加速度，ez=[0,0,1]T为常值向量；m为四旋翼无人机质量；τf为无人机的总升力；τ为无人机x,y,z这3个方向的控制力矩；I=diag(Ix,Iy,Iz)为无人机惯性常值矩阵；Δ1(t)、Δ2(t)为综合干扰。包括模型参数不确定及外界干扰，旋转矩阵R和变换矩阵W定义为

R=

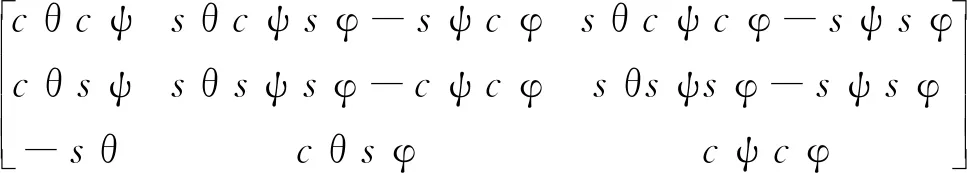
(5)

(6)

式中：cθ=cosθ,sθ=sinθ，下同。控制量[τf，τ1,τ2,τ3]T与电机转速ω=[ω1,ω2,ω3,ω4]T之间的关系为

(7)

图1 无人机模型示意图

本文控制目标为：针对无人机轨迹姿态模型式(1)～式(4)，设计集群无人机路径规划算法和轨迹姿态跟踪控制器，实现集群无人机安全、迅速的队形重构。

2 集群无人机路径规划

本节将针对集群无人机路径规划问题，利用CAPT算法及无人机轨迹平滑方法，实现多无人机队形重构过程中的并行目标分配和轨迹生成。

2.1 CAPT算法

CAPT算法[10]是Kumar团队提出的基于无标号问题的解决方案，可以解决集群由同构个体组成且目标位置可以任意分配的运动规划问题。本文研究的集群无人机队形重构问题，只要求形成特定的队形形状，而不关心每架无人机的具体位置，可以转化成无标号问题，因此可以采用CAPT算法求解。

考虑集群无人机队形重构问题，假设集群无人机规模与无人机目标位置数量相同为N，第i架无人机的初始位置为xi∈Rn，第j个目标位置gj∈Rn。解决无人机队形重构问题需要对无人机目标位置进行分配同时产生到达各个目标的安全轨迹。

(8)

定义增广分配矩阵Φ≡φ⊗In，⊗代表求取克罗克内积。

CAPT算法的目的在于规划轨迹p(t)→X(t)(t∈[0，T])，T为所有无人机到达最终位置的终止时间，将在后文进行说明。运动轨迹p(t)满足始端约束条件p(0)=X(0)和终端约束条件ΦTp(T)=G。

假设初始位置与目标位置、各无人机之间的距离满足

(9)

CAPT算法将无标号问题看做最优化问题进行求解，确定最优的分配方案和轨迹，最优化目标函数为

(10)

问题的解由直线轨迹组成，且各无人机走过的距离的平方之和最小。即最优分配方案为

(11)

其中分配问题φ*可以用匈牙利算法进行求解。

所有的机器人都是在一定时间之内到达目标位置，所有无人机到达最终位置的终止时间T为

(12)

p*(t)=(1-δ(t))X(0)+δ(t)ΦG

(13)

2.2 无人机轨迹平滑方法

为了满足四旋翼无人机的动力学方程，需要对轨迹进行平滑，Mellinger和Kumar[22]证明了最小化位置状态的四阶导可以实现对于轨迹的平滑追踪。代价函数为

(14)

问题(14)的最优轨迹与式(10)所求直线轨迹相同，δ(t)为高阶时间多项式。

本文中为了实现对轨迹的精确平滑追踪，同时对位置、速度和加速度进行控制，由文献[23]中的最小化三次可微运动的方法，将δ(t)表示为5阶 时间多项式函数。利用文献[23]中给出的不同终端约束条件下的最优状态轨迹参数表达式，在固定位置、固定速度和固定加速度的情况下，将位置状态求取p(t)→X(t)(t∈[0,T])进一步扩展成求取包括位置、速度、加速度在内的状态轨迹s(k)=[pk,vk,ak]，其中：pk、vk、αk分别为X、Y、Z坐标系中单架无人机在某一时刻某一坐标维度的位置、速度和加速度。注意此时只针对X-Y-Z坐标系中的单架无人机轨迹进行求取，即求得的是单架无人机在某一时刻某一坐标维度的位置、速度和加速度状态信息。

状态轨迹参数为

(15)

定初始状态向量s(0)=[p0,v0,a0]。终端状态向量s(T)=[pf,vf,af]，则

(16)

最优状态轨迹为

(17)

在本文研究的集群无人机队形重构问题中，采用“悬停-运动-悬停”的运动模式，给定s(0)=[p0,0,0]和s(T)=[pf,0,0]，代入式(15)～式(17)中，得到最优状态轨迹：

(18)

(19)

3 四旋翼无人机轨迹姿态控制

基于第2节路径规划所设计的无人机轨迹，本节将分别针对无人机位置环及姿态环，设计有限时间多变量滑模控制及姿态解算算法，实现干扰影响下的无人机位置-姿态跟踪控制。

图2 无人机位置-姿态控制原理图

3.1 位置环控制器设计

定义位置误差e1=p-pref，基于式(1)和式(2)， 可得

(20)

本文所设计的控制器包括2部分：标称控制器un及补偿控制器ud，即

u=un+ud

(21)

其中，标称控制器un用于保证无综合干扰(外加干扰及模型参数不确定综合)影响下系统的稳定跟踪控制；而补偿控制器ud则用于保证对综合干扰的抑制。故位置环实际控制输入为

τf=mu(Rez)

(22)

下面将分别介绍标称控制器un和补偿控制器ud的设计过程。

步骤1标称控制器设计

针对标称系统：

(23)

引理1[16]针对积分链系统：

(24)

定义k1,k2,…,kn>0使sn+knsn-1+…+k2s+k1是Hurwitz的，且存在ε∈(0,1)使得对于每个r∈(1-ε,1)，如果采用如下反馈控制器：

(25)

式中:r1,r2,…,rn满足

(26)

且rn=r,rn+1=1，那么系统式(24)是有限时间收敛到平衡点的。

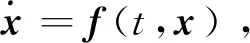
(27)

式中:V(x0)为V(x)的初值；Treach为收敛时间。

考虑标称系统式(23)，设计标称控制器为

(28)

式中：k1,k2>0。

将式(28)代入标称系统(23)可得

(29)

故由引理1及式(29)可知，标称控制器式(28) 能够保证系统式(23)的有限时间收敛。然而系统式(23)未考虑外界干扰和系统内部不确定等综合干扰的影响，因此，下面将给出连续补偿控制器设计过程，用于对系统的综合干扰进行处理。

步骤2补偿控制器设计

设计积分滑模面：

(30)

式中：e2(0)为e2(t)的初值。由式(30)可以看出，当t=0时，滑模面s=0，即系统初始状态就位于滑模面上，避免了趋近滑模的过程，能够保证整个过程的鲁棒性。

对积分滑模面(30)求导，可得

(31)

ueq=un-d(t)

(32)

代入系统(20)可得

(33)

通过比较式(33)及式(23)可得，当系统状态到达滑模面s后，综合干扰影响下的系统即转化为标称控制系统，基于所设计的标称控制器(28)即可实现系统的有限时间稳定。因此，此时的控制目标转变为：设计补偿控制器ud，保证系统状态有限时间内到达滑模面s。

对式(31)再次求导，可得

(34)

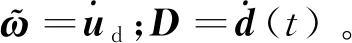
根据式(31)和式(34)，设计虚拟控制ϖ为

(35)

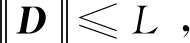
式中：α>2L为正常数。

而真实控制器为

(36)

由式(35)和式(36)可以看出，不连续量出现在虚拟控制输入ϖ中，而真正的补偿控制输入ud是连续的，因此能够有效减少抖振，提高控制精度。

定理1考虑综合干扰影响下的跟踪控制系统式(20)，在假设1成立的条件下，如果控制器设计为式(21)，其中标称控制器un设计如式(28)所示，补偿控制器ud设计如式(36)所示，那么存在一系列常数00,k2>0，α>2L，使得系统状态跟踪误差是有限时间收敛到零的。

(37)

定义以下Lyapunov函数：

(38)

式中：γ为待设计正常数。式(38)可重新书写为

(39)

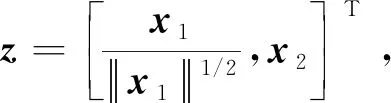
(40)

(41)

(42)

由式(42)可知，如果矩阵A>0那么矩阵P1>0。由于

(43)

因此，式(41)可以写为

(44)

由此可见，Lyapunov函数V是正定的。对V求导，可得

(45)

(46)

(47)

如果参数α,γ满足下列条件：

(48)

(49)

基于式(44)和式(49)，式(46)可以写为

(50)

3.2 姿态解算算法

四旋翼无人机无法通过控制力矩直接对飞行轨迹进行控制，需要对式(21)中位置控制器得到的控制指令进行姿态解算，转化为期望的飞行姿态。本文中采用悬停控制思想，追踪期望位置pref和期望偏航角ψref=ψ0，姿态解算算法[25]为

(51)

式中：φref、θref、ψref分别为期望的滚转角、俯仰角和偏航角。且期望加速度accref=-gez+u+Δ1(t)，accrefj(j=1,2,3)表示向量accref的第j个元素。

3.3 姿态控制器设计

(52)

等同于位置环控制器设计，可进行姿态跟踪控制器ua的设计。姿态控制器包括2部分：

ua=una+uda

式中:标称控制器una用于保证无综合干扰(外加干扰及模型参数不确定综合)影响下系统的稳定跟踪控制；而补偿控制器uda则用于保证对综合干扰的抑制。标称控制器及补偿控制器分别设计为

(53)

最终得到姿态环控制力矩为

τ=IW-1ua

(54)

3.4 仿真校验

为验证设计的轨迹姿态控制算法的有效性，在MATLAB环境下对单架无人机进行仿真，仿真采样频率设置为0.001，仿真过程中各参数选取如下：

1) 四旋翼无人机物理参数：质量m=0.5 kg，惯性参数Ix=2.3×10-3kg·m2，Iy=2.4×10-3kg·m2，Iz=2.6×10-3kg·m2，旋翼转动中心到无人机中心的距离d=0.225 m，旋翼的升力系数kF=5.55×10-8N·m· s2/rad2，旋翼的扭矩系数kM=2.5×10-9N·s2/rad2。

2) 期望轨迹pref=[sint,cost,sint]，期望偏航角ψref=0 °，所受干扰为Δ1=Δ2=[0.1sint，0.1cost，0.1(sint+cost)]，初始值p0=[2,-3,2]T,v0=[0,0,0]T，Θ0=[0.2,-0.3,0.2]T，Ω0=[0,0,0]T。

3) 控制器参数：位置控制器k1=5,k2=4,r1=1/2,r2=5/7,α=5。姿态控制器k3=12,k4=5,r3=1/2,r4=5/7,β=4。

仿真结果如图3～图5所示。由图3和图4可知，在综合干扰影响的情况下，位置跟踪误差及姿态跟踪误差均可以在有限时间内收敛到零。

图3 位置跟踪误差

图4 姿态跟踪误差

总控制量[τf，τ1，τ2，τ3]T的仿真结果如图5所示，可以看到控制输入连续且稳定，系统在一定外界干扰的情况下仍能保持稳定，且取得良好的轨迹姿态跟踪效果。由图3～图5的仿真结果可以有效验证所提控制算法的有效性。

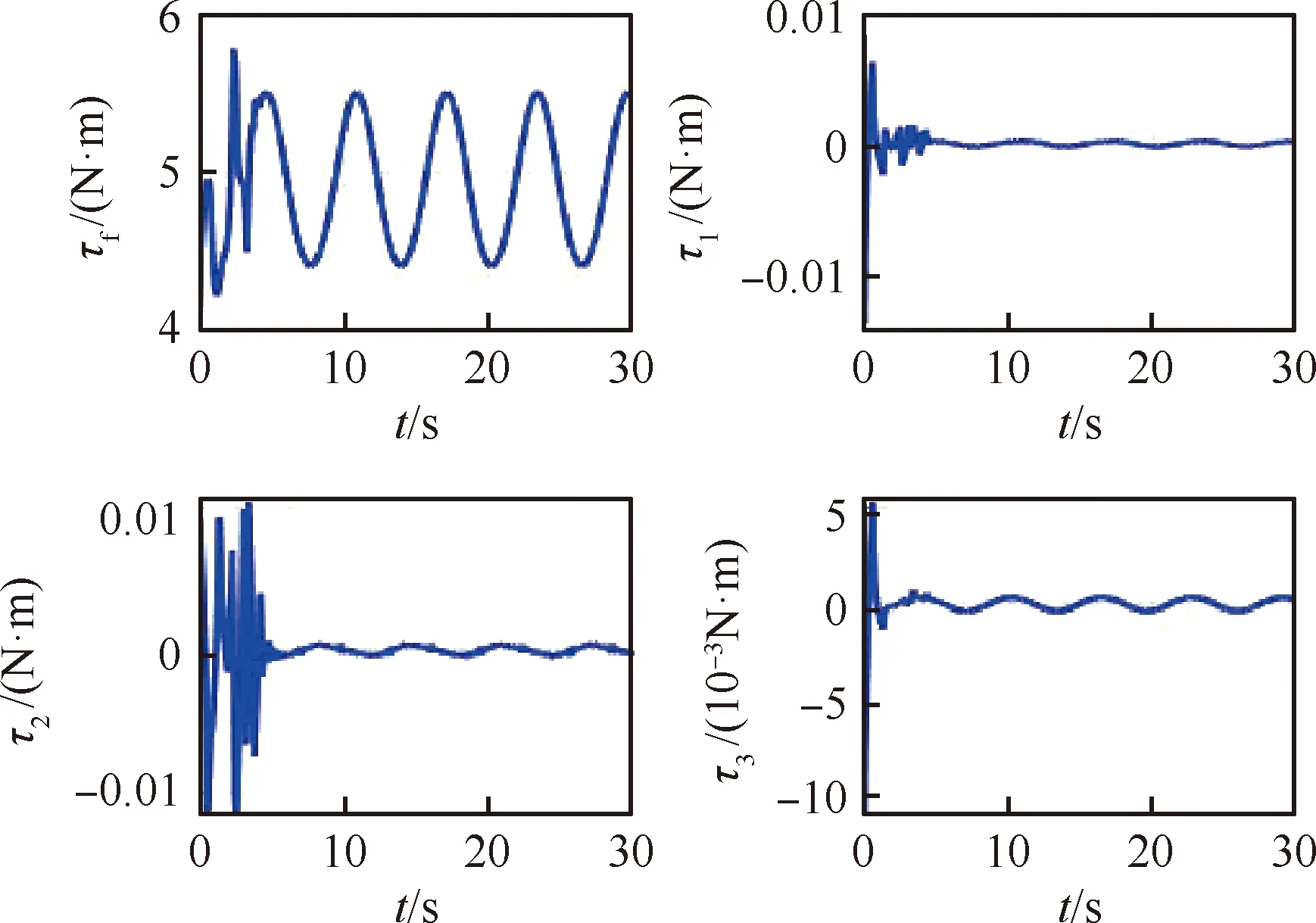
图5 控制输入

4 仿真平台搭建与效果验证

4.1 仿真平台基本结构

集群无人机队形重构即一定数量的无人机根据特定任务需求，从一个队形变换形成另一个新的队形形状。需要考虑的问题涉及目标位置分配、路径规划、避撞要求、姿态轨迹跟踪控制等多个方面。要对上述问题分别考虑控制策略，并以一种直观可靠的方式对控制算法进行验证和效果对比，就需要进行综合虚拟仿真实验。

本文采用的Gazebo仿真软件，是基于ROS操作系统的一款三维物理仿真软件，与ROS操作系统配套使用，可实现完整的“建模-仿真-可视化”的仿真流程，与MATLAB仿真相比，Gazebo仿真更贴近真实物理情景，仿真的实时性和真实性更强，同时能够克服MATLAB仿真曲线表示缺乏直观性的缺点，实现仿真结果的三维立体视景演示。Gazebo软件中可以搭建近似于现实世界的仿真场景，构建多种传感器仿真模型，搭建包括无人机在内的各种机器人模型，包含多个物理仿真引擎，由此可以为机器人模型添加现实世界的物理性质，使仿真对象满足贴近真实的运动学和动力学物理要求。

仿真平台的基本框架如图6所示。其中ROS作为机器人开源的元操作系统，主要承担对于控制器算法的实现，通过编写路径规划算法、无人机控制算法等C++代码，实现对无人机的位置、姿态等状态的控制；Gazebo仿真软件作为一个可视化的图形用户界面，需要在其中搭建仿真场景、传感器模型、仿真无人机等，通过Gazebo-ROS bridge与ROS系统建立连接，实现无人机模型状态的获取与发送，可视化地演示集群无人机队形重构的整体流程效果。平台各个部分描述见4.2节和4.3节。

图6 Gazebo-ROS仿真平台架构

4.2 搭建仿真场景

Gazebo仿真软件是一个功能完善的3D机器人仿真软件，通过Gazebo搭建无人机仿真的整体场景，包括搭建仿真环境和无人机模型，添加传感器、执行器等各种插件，实现ROS与Gazebo的连接等环节，主要操作流程如图7所示。其中URDF文件是Gazebo-ROS中的一种用于描述机器人组件的XML文件，该文件的主要功能就是描述机器人各个部分(link)与关节(joint)的属性，创建机器人模型。.world文件是对仿真环境的描述，通过.launch文件启动并加载仿真场景，由此实现Gazebo中仿真模型的整体搭建。详细操作步骤参考Gazebo软件官方说明[26]，此处不再赘述。

图7 Gazebo仿真流程

4.3 集群无人机飞行控制的实现

本文中基于无人机灯光秀场景，设计实现对集群无人机进行队形重构的整体流程演示，每架无人机都由相同的控制系统框架进行控制，总体仿真演示方案如图8所示，其核心包括轨迹规划模块和轨迹跟踪模块，其中轨迹规划模块包括队形设计和路径规划2个子模块，队形设计子模块针对无人机表演的队形形状进行队形设计，路径规划子模块为每架无人机从起始点到目标队形最终点的轨迹进行规划设计；轨迹跟踪模块，主要利用本文第3节中的轨迹姿态控制器，通过内环的姿态控制和外环的位置控制，确保每架无人机都能够安全地、无碰撞地追踪给定轨迹朝着各自目标位置飞行。

图8 集群无人机队形重构仿真方案

4.4 仿真验证

以12架四旋翼无人机为例，对上述提出的路径规划算法及轨迹姿态控制器的有效性进行数值仿真验证。12架四旋翼无人机集群飞行的飞行示意图如图9所示，两队形之间的详细队形重构过程如图10所示。图中标注实时追踪2架无人机(无人机6和无人机7)的实时位置变化。由图9可以看出仿真实现了连续的队形重构过程，显示了各队形重构后无人机的位置变化情况，其中由队形1到队形2的变换过程中无人机6的位置几乎不变，体现了队形位置最优分配保证效率最高的思想。由图10可以看出在两队形重构过程中，无人机间均保持一定的飞行距离，确保相互之间不会发生碰撞。总结可得基于本文的控制算法，利用CAPT算法进行集群无人机路径规划，可以实现多无人机的连续、安全、无碰撞的队形重构过程。

图9 12架无人机队形重构

5 结 论

1) 研究了路径规划CAPT算法和无人机轨迹平滑方法，针对无人机集群队形重构的具体场景需求，实现多无人机安全迅速的并行目标分配和轨迹生成。

2) 针对无人机轨迹姿态跟踪问题，提出了一种有限时间多变量积分滑模控制算法，实现了对无人机期望轨迹的有限时间精确跟踪。

3) 基于Gazebo-ROS搭建了无人机仿真平台，基于实际物理引擎及多种动力学插件实现了集群无人机队形重构“建模-仿真-可视化”的一体化虚拟仿真演示，对上述控制算法及路径规划算法进行了有效性验证。