BP神经网络在连续梁桥线型控制中的应用

郭 挺， 严万双

(武汉理工大学，湖北 武汉 430061)

0 引 言

连续梁桥常采用悬臂浇筑法施工,施工过程比较复杂,受到诸多因素的影响,因此桥梁实际结构与设计状态之间必然存在误差。随着施工的推进,桥梁悬臂不断加长,刚度不断变小,误差会不断累积,如果不及时控制和进行调整,误差会累积到很大的程度,对桥梁的顺利合拢和结构安全造成严重威胁。因此需要在施工的过程中进行施工监控,保证桥梁的线型和内力满足设计要求。所以施工监控中标高控制成了桥梁施工过程中一个很重要的部分,准确预测桥梁的挠度是标高控制的重点。本文利用神经网络对湖南怀化市下垄舞水大桥监控数据进行网络训练和预测,探讨神经网络在桥梁线型控制中的应用。

1 BP神经网络

1.1 BP神经网络基本概念

BP神经网络是一种多层前馈神经网络,它的特点是在传播过程中信息前向传播,误差后向传播。常采用的方法是梯度下降法。过程如下:

(1)信息正向传播。收集样本,输入到输入层,经过各层隐层单元的处理,传到输出层,输出结果,并与期望值相比较,如果与期望值的误差不满足要求,则反向传播误差,否则训练结束。在此过程中每一层神经元的状态只会对下一层神经元产生影响。

(2)误差反向传播。如果正向传播输出值与期望值的误差不满足要求,则需进行反向传播,此时误差信号按照信息正向传播的道路反着传递回去,在这个过程中修改隐层的权值,使误差减小。即在反向传播中,误差决定了各隐层权值的改变量。

1.2 BP神经网络模型

BP神经网络模型如图1所示。在运用其进行预测前,需要对其先进行训练,通过训练使得模型预测结果与预期趋于拟合,然后将此模型存储,用于之后的预测使用。

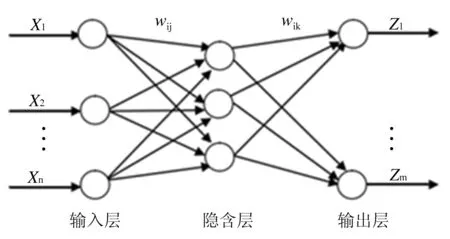
图1 三层BP神经网络模型

对BP神经网络的训练步骤如下:

(1)初始化神经网络。根据输入输出序列确定输入层节点数(n)、隐层节点数(l)、输出层节点数(m)，确定参数后初始化权值ωij与ωjk、隐含层阈值α和输出层阈值b、学习速率η和网络激励函数f(x)。

(2)输入隐含层并计算输出。根据输入的变量x、权值ωij及隐含层阈值α计算各隐含层输出值。

式中:l表示隐含层的节点数；f(x)表示激励函数。

(3)输出层计算输出。BP神经网络预测结果为：

式中:H为隐含层输出值;ωjk为隐含层与输出层的连接权值;b为阈值。

(4)计算网络误差值。根据网络输出层输出结果O值和期望值(真值)Y,计算模型预测误差e,表达式为:

ek=Yk-Ok,k=1,2,3,…,m

(5)更新连接权值和阈值。BP神经网络的训练原理,就是对模型网络中各层权值和阈值的调整,调整各层权值就可改变误差,常采用梯度下降法使误差减小。根据网络计算预测值的误差,进行误差反向传播,更新权值和阈值如下:

bk=bk+ek,k=1,2,…,m

(6)检查网络总误差是否达到要求的精度,如果达到次数达到上限为止。

1.3 BP神经网络特点

BP神经网络是一种非线性系统,主要具有以下几个特点:

(1)强大的非线性映射能力。BP神经网络无须事先了解输入输出的映射关系,BP算法的前馈网络能够很好地学习和储存这种映射关系。只要学习样本足够多,便能够完成从输入层到输出层的非线性映射。大量学者通过研究证明了BP神经网络适用于大量复杂的非线性问题。

(2)自学习和适应能力强。BP神经网络自动学习,生成输入层与输出层之间的合理激励函数规则,并将学习到的内容存储下来。

(3)泛化能力强。泛化指的是在某种刺激下形成一定的反应后,在其他类似的刺激下也能形成相似的反应。BP神经网络在见到不是样本的数据的进行训练时,也能够完成从输入层到输出层的正确映射。

2 应用实例

在连续梁桥悬臂施工的过程中,在刚开始的几个节段,立模误差往往较小,但是随着悬臂长度的增加和误差的不断累积,后续节段的误差可能会变得较大,对桥梁的线型产生不利影响,甚至使桥梁不能顺利合龙。因此对悬臂过程的后续节段立模误差进行有效的把握是十分重要的。本文考虑将BP神经网络模型应用于悬臂施工后续节段的立模误差预测中,并讨论其优劣势,验证其合理性。

本文以下垄舞水大桥的施工监控为例,采用BP神经网络对施工过程下一节段实际挠度进行预测,进而得出合理的预拱度和立模标高。BP神经网络模型包含输入层、隐含层、输出层。输入层神经元的数量取决于对桥梁线型影响较大的因素数量。输出层输出的结果表示为该模型预测的挠度。隐含层神经元数量根据输出层输出层个数及隐含层层数确定。

2.1 工程简介

下垄舞水大桥桥址位于湖南省怀化市,桥梁依次跨越沪昆客专隧道、规划高堰路、G65包茂高速、规划舞阳大道、舞水、G209国道。本桥为无砟轨道预应力混凝土双线连续梁高速铁路桥,桥跨布置为(48+80+48)m,混凝土梁体为单箱单室、变高度、变截面箱梁,桥面宽12.6 m。梁桥上构造型简洁,规格与外形标准化,具有足够的刚度与强度,能满足列车平稳运行的需求。

成桥后理论挠度值如图2所示。

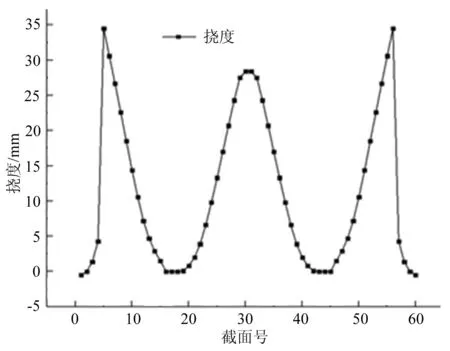
图2 合拢后主梁挠度

2.2 网络模型参数选取

2.2.1 输入输出参数确定

在桥梁施工控制中,影响桥梁实际标高的因素众多,如果将所有的因素都进行考虑并作为BP神经网络的输入层,是不合理且不经济的。因为非关键性因素会干扰网络的相应,降低网络性能,而且还会加大网络计算量。本文根据大量工程经验,选取三层BP神经网络层,输入向量为挂篮弹性变形、测量温度、距T构中心距离、距0#块浇筑时间、理论挠度、前一节段挠度、待施工节段理论挠度,以待施工节段挠度为输出向量。

2.2.2 数据归一化

不同类型的数据具有不同的量纲和量纲单位,这会导致大数据淹没小数据的情况出现,为了消除不同量纲的影响,需要将数据归一化,以增强不同类型数据间的可比性。原始数据进过标准化处理后,处于同一数量级,适合进行综合对比。

本文采用的归一化函数如下:

考虑到训练函数Sigmoid函数在(0,0.05)和(0.95,1)的区间内曲线较为平坦,网络训练易陷入平坦区,因此令归一化后的数值处于[0.05,0.95]区间内,取a=0.05,b=0.95。当完成预测后,对预测数据需要进行反归一化处理,将其还原为原有量纲,处理公式为:

2.3 网络训练

训练数据来自于张吉怀铁路下垄舞水特大桥施工监控项目,将1-6节段数据作为训练数据。训练效果如图3所示,可以看出训练效果较好,模型对训练样本数据拟合程度较高。

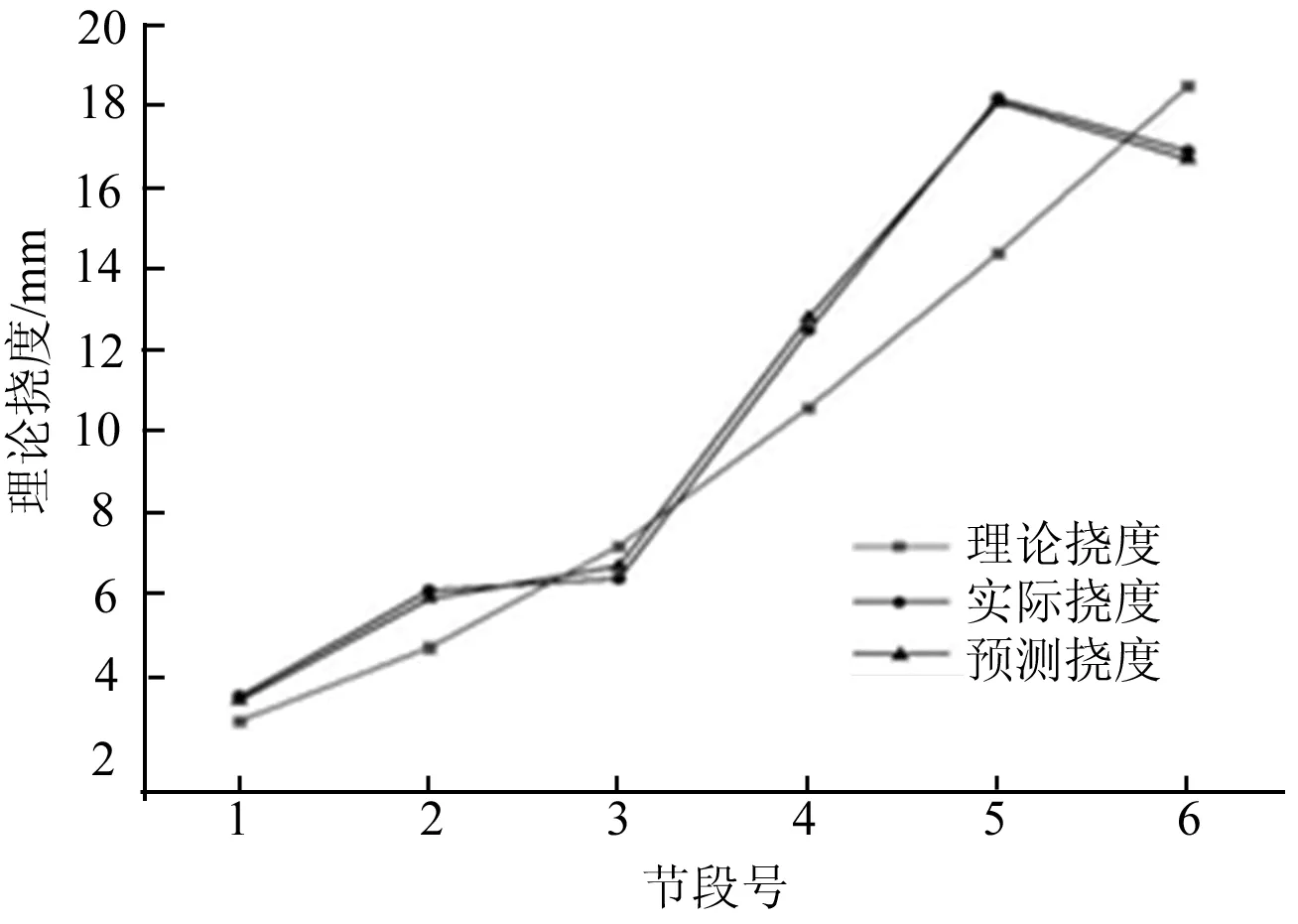
图3 训练样本拟合结果

2.4 实际应用

在采用悬臂浇筑法施工的连续梁施工过程中,根据大量工程实际经验,前几个节段的变形误差相对后几个节段的变形误差较小,并且后续节段对桥梁能否顺利合拢起到十分重要的作用。在通常的桥梁施工控制中,以理论挠度与实际挠度间会产生一定的误差,但在设置预拱度时通常忽略此误差,这样可能会导致实际标高与设计标高产生较大误差,影响桥梁受力和桥面行车舒适,线型误差过大时甚至会对桥梁安全产生威胁。本文利用BP神经网络构建模型,对未施工节段的变形误差进行预测,并将此模型计算结果应用于桥梁预拱度设置中。

利用训练过的BP神经网络模型,将上述输入向量输入该模型,得到各施工节段的预测挠度数据及误差如图4所示,可以看出,预测结果较好,使用BP神经网络建模预测的挠度相比于计算的理论挠度更接近于实际挠度。

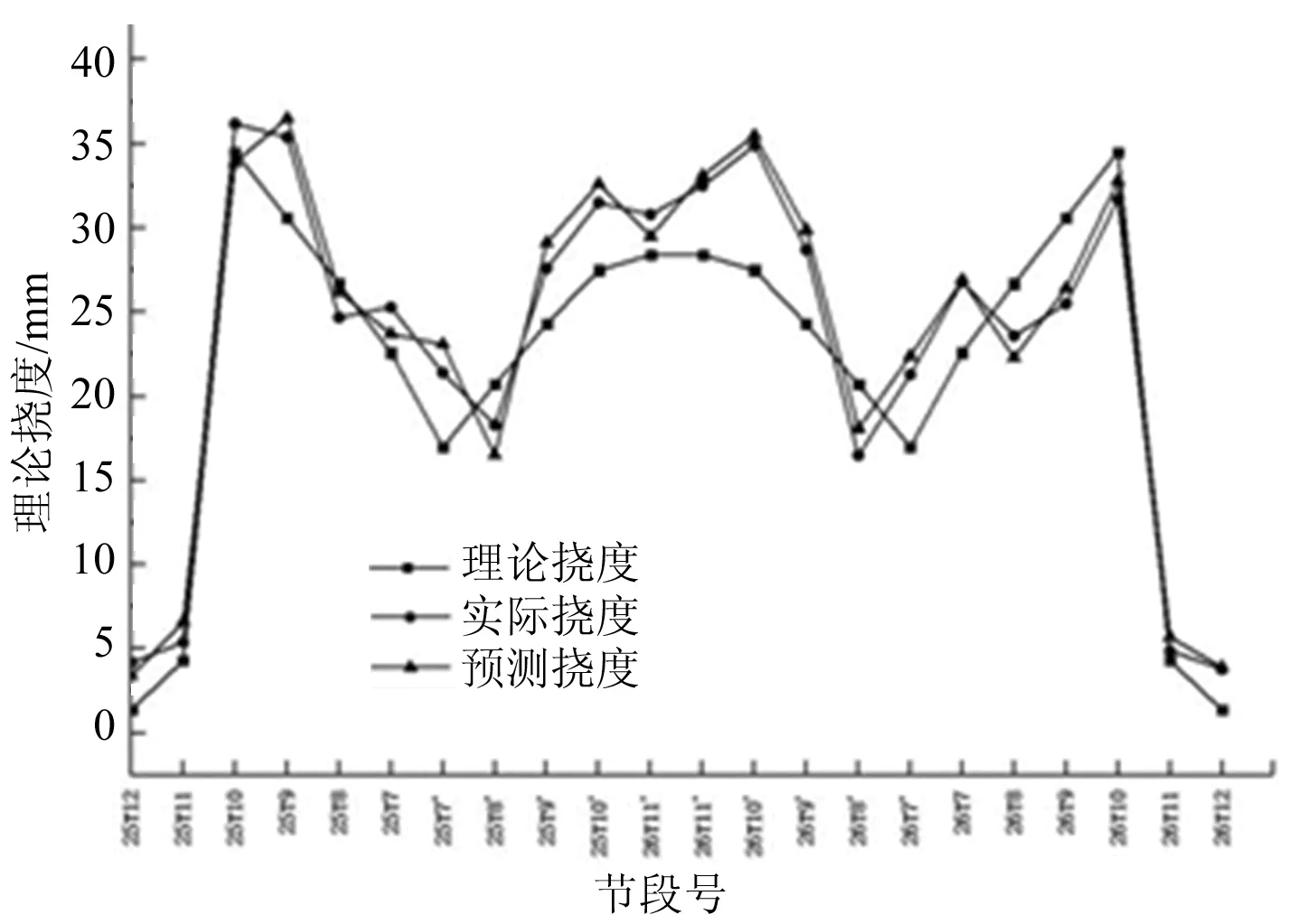
图4 BP网络模型预测结果

本文将BP神经网络模型用于连续梁悬臂浇筑法施工中桥面挠度的预测,其预测结果与施工完成后实际挠度较为接近,说明此方法适用于预测采用悬臂浇筑法的连续梁桥挠度。并以此模型的预测挠度结果用于调整预拱度指令,从成桥成后的梁顶高程可以看出,梁顶实际高程与设计高程相差值大部分在[-10 mm,20 mm]内,如图5所示，符合高速铁路桥规范,达到了施工监控预期目标。构建BP神经网络模型预测挠度后的节段标高误差绝对平均值相比之前未使用BP神经网络模型预测挠度的1-6节段显著降低。中跨合拢段两侧的高程误差为5.9 mm,符合高铁桥梁合龙误差规范要求,且控制在了一个较好的范围。表明BP神经网络模型在调整桥梁施工预拱度上起到显著作用,在实际工程中具有较高的应用价值。

图5 成桥后标高误差

3 结 论

本文以湖南怀化下垄舞水大桥线型监控为例,将BP神经网络训练用于桥面实际变形值的预测中,其预测结果与事后的实际值差距较有限元软件计算值小,表明该方法应用于桥梁施工监控中是可行的,应该认为是一种值得参考的方法,可与常用方法互相补充。但是桥梁的变形下挠是一个复杂的过程,BP神经网络并未探究其本质的变化规律,这需要我们更加深入地探索学习,同时,应该研究更高效的算法,以提高神经网络的效率和精度。