基于stacking组合模型的轨道交通换乘站短期客流预测

池贤昭， 陈 鹏， 祝佳莉， 耿小情

(武汉理工大学 交通学院，湖北 武汉 430063)

0 引 言

面对迅猛增长的地铁建设现状,以及智慧城市和智能交通的发展需要,实时精确的客流预测作为智能交通的重要支撑就显得尤为重要。轨道交通短期客流预测通过对地铁站历史刷卡数据的分析,预测站点未来的客流量变化,帮助实现更合理的出行路线选择,规避交通堵塞,提前部署站点安保措施等,可以最终实现用大数据和人工智能等技术助力未来城市安全出行。

现有研究大都从地铁客流的周期性或者随机性出发,针对性的提出预测方法。比较经典的方法有时间序列法[1,2]、非线性回归法[3,4]、参数回归法[5-7]等。近年来,很多学者考虑到实际客流的复杂性和单一预测模型的片面性,针对不同的客流状况,尝试利用组合模型来预测短期客流。通过选取两种或两种以上的客流预测方法进行组合,提高预测精度,实现优势互补。郝晓涛[8](2016)根据交通流特性,在交通流时间序列数据聚类分析(CA)的基础上,通过WNN神经网络模型和ARIMA时间序列统计模型的组合模型来预测交通流,相较于传统的短时交通流预测模型,组合模型在预测精度、预测速度和稳定性上都有了明显的提高。高杨等[9](2016)以小时客流量为预测时间粒度,构造一种基于组合误差优化模型的城市轨道交通短期客流预测模型。模型预测效果良好,但考虑因素单一,忽略了时空、客流属性、票价以及车站运输能力等多维度因素的影响。Guo等[10](2019)考虑轨道交通客流预测中异常客流的随机性和波动性,在提取异常客流特征的基础上,构建了一种基于支持向量机回归和长短时记忆神经网络的混合预测方法。但混合方法仅适用于预测15min内的客流量。

本文基于短时客流的随机波动性,考虑客流序列的时间特性和组合模型和泛化性,提出了一种基于stacking算法的轨道交通短期客流组合预测方法。该方法能够较为精确的预测随机性和波动性较大的客流,一定程度上克服了组合模型泛化性能不强的缺陷。

1 GGRK-MLP组合模型介绍

1.1 组合预测算法简介

组合预测也可称为集成学习预测,组合预测的一般结构如图1所示，先产生一组“个体预测器”,再用某种策略将他们结合起来[11]。

图1 组合预测一般结构

stacking算法的基本思想是学习几个不同的弱学习器,并通过训练一个元模型来组合它们,然后基于这些弱模型返回的多个预测结果输出最终的预测结果。因此,为了构建 stacking 模型,需要定义想要拟合的L个学习器和组合它们的元模型。

1.2 GGRK-MLR组合模型

本文提出的GGRK-MLR组合模型基于stacking算法,将梯度提升回归(GBR)、随机森林回归(RFR)以及K近邻回归(KNN)作为初级学习器,多层感知器回归(MLR)作为次级学习器,并采用10次10折交叉训练避免初级训练模型与次级训练模型过拟合。

1.2.1 梯度提升回归和随机森林回归

梯度提升回归是一种通过构建多个分类回归决策树并将之组合形成强学习器的集成模型。梯度提升属于提升算法体系的一种,其基本思想是利用损失函数的负梯度在当前模型下的值作为模型本次训练结果残差的近似,并以该值作为下一次训练的目标[12]。对于样本N={(x1,y1),…,(xn,yn)},若使用最小二乘回归为损失函数,则损失函数的负梯度就是预测值与真实值的残差,其表现为:

=yi-Fm-1(xi)

(1)

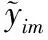
梯度提升回归建立在多个弱学习器的基础上,采用连续的方式构造树。第m个学习器在前m-1个弱学习器的误差上重新进行训练,更新样本权重,这就导致模型不会过度学习异常值特征,即预测值较为平稳。在数据量相对较小的情况下,梯度提升回归也可以达到很好的预测精度,同时用到了强预剪枝,从而使得梯度提升树往往深度很小,这样模型占用的内存少,预测的速度也快。

随机森林回归与梯度提升回归一样,都是建立在分类回归树基础上的集成模型。与梯度提升最大的不同在于,随机森林在构造过程中运用的随机化方法,即随机选择构造每棵树的样本集,随机选择每个节点用于划分的特征,这导致随机森林中每棵树之间都没有关联不会造成过度拟合的现象。值得注意的是,由于随机森林对于数据集合特征划分的随机性,模型过度学习异常值(数据样本量小)特征,导致预测结果更多的偏向异常值。

1.2.2 K近邻回归

K近邻回归原理与K近邻分类算法类似,主要通过对于与预测特征(值)某种距离内的k个训练值,划分目标特征(值)的类别(值)从而得到预测的类比或者具体值。KNN有三大要素,分别为近邻值k、度量距离d以及决策方式F(x)[13]。

KNN回归对于特征向量不太多的数据有较好的应用,理论成熟、思想简单。对于客流复杂的轨道交通换乘站点,在5min时间粒度内客流的关联性较大,因此可以通过KNN回归来拟合短时间内的客流变化特征。

1.2.3 多层感知机回归

多层感知机(MLP)是多个单层感知机的组合。感知机也称为感知器,是一种双层神经网络,即只有输入层和输出层而没有隐层的神经网络。多层感知机的本质就是通过在输入层和输出层之间加入一层或多层隐层,建立起来的神经网络模型,并且每一层和前一层通过一个系数矩阵连接。

MLP基于BP算法,因此在训练的过程中,模型会持续的更新参数的权值,所以MLP模型也能够有效的学习数据的不同特征,分配合理的权重,达到整合不同特征优势的作用。

1.2.4 GGRK-MLR组合模型

GGRK-MLR组合模型基于stacking算法,其基本步骤为:首先,对客流的原始数据进行汇总,然后提取数据的时间特征,并对数据进行归一化处理。其次,将输入数据导入到设定好参数的初级训练模型(GBR、GBR、RFR、KNN)中进行训练,整理训练得到的数据形成次级矩阵的输入矩阵。最后,将输入矩阵导入次级训练模型(MLR)中进行训练,得到训练好的GGRK-MLR模型。具体遵循以下步骤:

(1)数据预处理。

①客流数据汇总。将原始客流数据进行汇总,汇总后的历史客流数据为Q。

②提取汇总数据的时间特征。简单的数据统计和相似日特征并不能保证预测的准确性。本文在汇总客流数据的基础上,提取客流数据的时间特性,提取每条数据的时间格式(%Y-%m-%d %H:%M:%S)所隐藏的星期、天、小时、分钟特性,分别形成“dayofweek”“day”“hour”以及“min”列,并添加到历史客流数据序列中。

③汇总数据归一化处理。考虑客流量数据之间的相互影响,将客流量数据进行归一化处理集体处理如下:

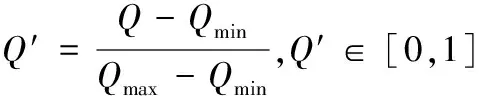
(2)

式中:Q为归一化预处理的历史客流数据;Qmin为Q中的最小值;Qmax为Q中的最大值;Q'为汇总后的历史客流数据。

(2) 训练初级模型和次级模型。经过数据预处理后,需要利用历史客流数据训练初级模型,得到训练好的初级模型。

次级训练器使用初级训练器训练得到的数据集,在一定程度上会造成次级训练器输出结果过拟合。为了克服这种限制,可以使用k-折交叉训练方法。

初级学习器会在k-1 折数据上进行训练,从而对剩下的一折数据进行预测。迭代地重复这个过程,就可以得到对任何一折观测数据的预测结果。这样一来,我们就可以为数据集中的每个观测数据生成相关的预测,然后使用所有这些预测结果训练元模型。

① GBR模型的p次k折交叉训练。对GBR进行p次k折交叉训练,则GBR模型p次k折交叉训练的结果平均值Qtra,gbr(p,k)为:

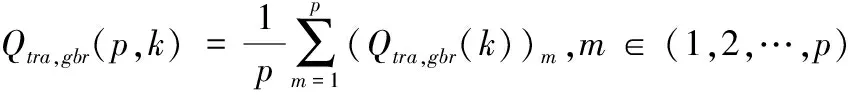
(3)

式中:Qtra,gbr(k)为GBR模型对Qtra进行k折交叉训练得到的的训练结果。

则训练好的GBR模型对验证集进行p·m次预测的平均值Qval,gbr(p,k)为:

(4)

式中：Gval,gbr,ij为GBR模型在测试集第i次第j折上的预测结果。

②RFR、KNN的p次k折交叉训练。同上,可以得到RFR、KNN进行p次k折交叉训练的结果Qtra,rfr(p,k),Qtra,knn(p,k),Qv al,rfr(p,k),Qv al,knn(p,k):

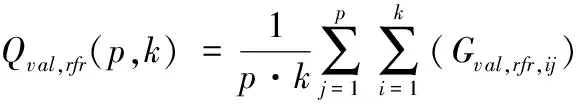
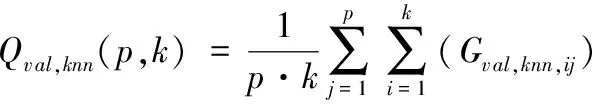
③ MLR模型训练。整理初级训练模型得到的数据以形成次级模型的输入矩阵。则次级训练器输入训练集Qtrac为:

Qtrac={Qtra,gbr(p,k),Qtra,rfr(p,k),Qtra,knn(p,k)}

(5)

次级训练器的输入测试集Qvalc为:

Qv alc={Qv al,gbr(p,k),

Qv al,rfr(p,k),Qv al,knn(p,k)}

(6)

将Qtrac和Qvalc输入到次级训练器MLR,得到最后测试集的预测结果A为:

A=MLR(Qv alc)

(7)

式中：MLR(Qvalc)为经过Qtrac训练好的MLR模型。

(3) 预测目标客流。

利用训练好的组合模型对目标值进行预测,得到预测值A,因为A为归一化后的预测值,所以还需要将A进行逆归一化处理得到实际的预测值,具体方式如下:

A′=Qmin+A·(Qmax-Qmin)

(8)

式中：A′为逆归一化之后的数据;A归一化预测值。

(4) 客流预测结果评价。平均绝对误差(MAE)能够更加真实的反映预测的误差情况,所以本文使用平均绝对误差对预测结果进行评价,MAE计算那公式如下。

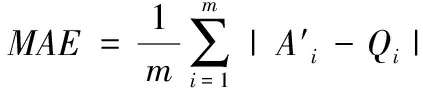
(9)

式中：m为预测客流的个数;Ai′为模型预测值;Qi为客流实际值。

2 实例分析

2.1 数据选取

本文选取杭州地铁4号线客流情况比较复杂的火车东站地铁站(stationID:15),分别对其工作日(1月24、25日)5 min出站客流,周末(1月26日)5 min的出站客流量进行预测。另外为验证模型在其他时间粒度上也具有较好的预测精度,对1月26日15 min、30 min为统计区间的出站客流量进行预测。本文数据基于杭州市2019年1月2-26日轨道交通售检票系统(AFC)进出站刷卡数据,原始数据包括刷卡时间、线路、站点、设备ID、支付类型、进出站状态以及用户ID等7种特征向量。具体表示见表1。

表1 杭州市轨道交通AFC原始客流数据特征表

考虑地铁站实际运行状态,将训练和预测全天时间段缩为05∶30至23∶30(序号1-216)并以5 min为时间粒度统计站点客流数量。本文针对工作日与周末分别使用历史相似客流数据作为训练集和验证集数据,并使用目标日的历史客流数据作为测试集数据。即:使用1月5、12、19日客流数据作为训练集和验证集,使用26日客流数据作为测试集数据;使用1月4、11、18日客流数据作为训练集和验证集,使用25日客流数据作为测试集数据;使用1月2、3、7、8、9、10、14、15、16、17、21、22、23日作为训练集和验证集,使用24日客流数据作为测试集数据。以上训练集数据和验证集数据均以7∶3分配。

2.2 参数设置

本文GGRK-MLP组合模型选取的具体参数如下:

Stacking算法:初级回归模型GBR、GBR、RFR、KNN,次级回归模型MLR,交叉验证的次数为10,折数为10,并行线数为6,得分函数neg-mean-squared-error;

GBR:损失函数为deviance,子模型数量为100,最大深度为3,节点分裂参与判断的最大特征数为none;

RFR:决策树个数为10,树的最大深度为none;

KNN:近邻半径k值为5,限定半径最近邻法使用的算法为auto,每个样本的近邻样本的权重选择函数为uniform;

MLR:权重优化器为adam,正则化参数为1e-5,输入和隐层数量为(150,4),随机种子数为72,最大迭代次数为2 000,随机优化大小为auto,学习速率为constant。

2.3 组合模型结果与分析

2.3.1 周末预测结果分析

对于1月26日杭州东站出站客流量的预测结果见表2，其组合模型预测值与实际客流量对比如图2所示。

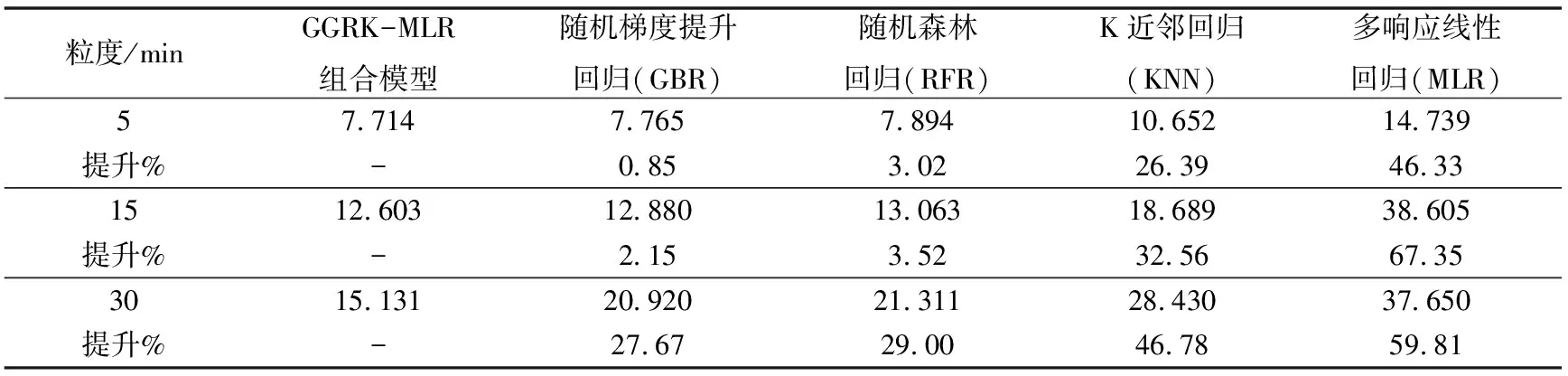
表2 1月26日杭州地铁火车东站出站客流量预测平均绝对误差(MAE)对比表

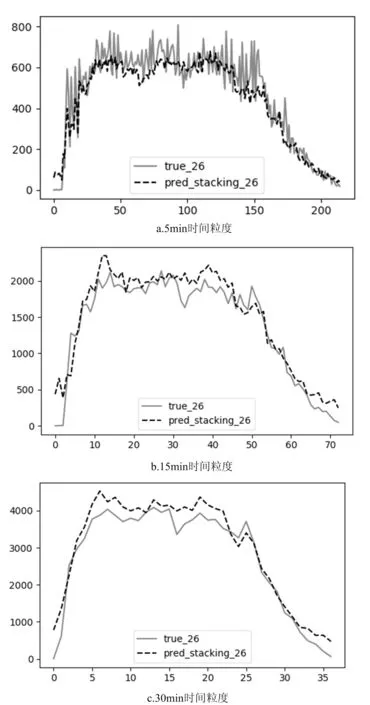
图2 1月26日组合模型预测值与实际客流量对比图

由表2可以看出,基于stacking的组合模型对杭州东站地铁站1月26日(周六)5min时间粒度进行的预测,stacking组合模型相对于随机梯度提升回归、随机森林回归、K近邻回归、多响应线性回归的平均绝对误差值MAE最小,因此组合模型具有更高的预测精度。组合模型的平均预测精度相对于GBR提升0.85%,相对于RFR提升3.02%,相对于KNN提升26.39%,相对于MLP提升46.33%。证明了组合模型在5 min时间粒度预测上具有更高的精度。从图2a可以看出(带*虚线为预测曲线),组合模型能够较好的拟合客流曲线。

表2中,组合模型对15 min和30 min时间粒度的客流量预测相对其他单个模型平均绝对误差最小,预测精度更高。证明了组合模型在更大时间粒度上也具有很好的预测精度,组合模型的鲁棒性和泛化性能更高。

从图2b、图2c上可以看出,在5 min时间粒度上,模型预测没有出现过拟合现象,但在15 min、30 min时间维度上预测出现了明显高于预测值的过拟合。三种维度的训练数据在输入特征向量的维度上是一样的,所以不考虑数据本身的影响。同时考虑到2月4、5日的除夕春节影响,城市轨道交通的客流量整体上会出现减少的情况,所以模型过拟合并不是数据的时间聚合维度原因,而在于组合模型没有学习春节临近客流量整体减少的趋势。

2.3.2 工作日结果分析

利用GGRK-MLR组合模型对24、25日的5 min客流量进行预测,预测结果见表3，预测值与实际客流量对比如图3所示。

表3 1月24、25日杭州地铁火车东站5 min出站客流量预测平均绝对误差(MAE)对比表

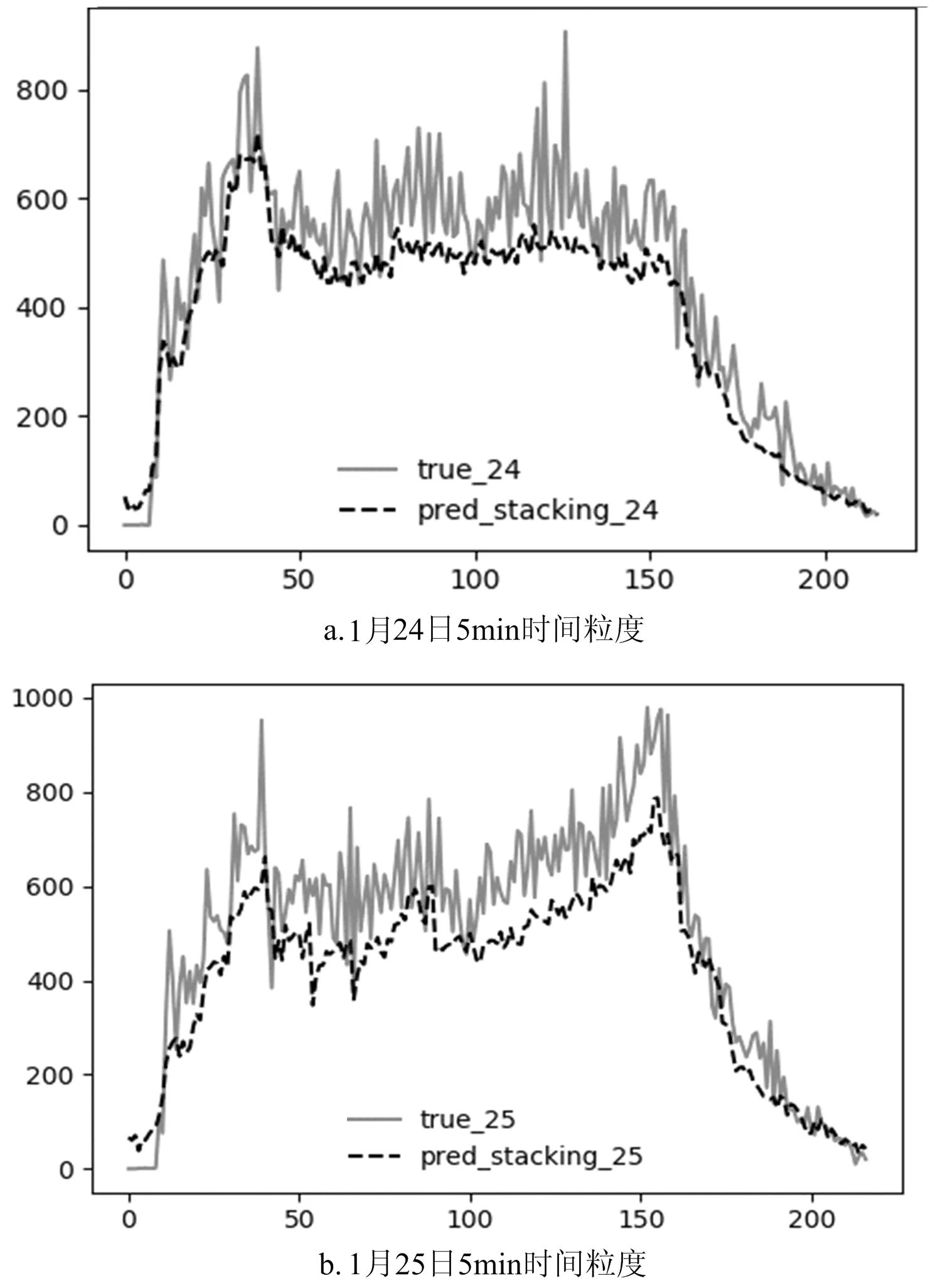
图3 1月24、25日组合模型预测值与实际客流量对比图

由表3可以看出组合模型在工作日上的预测MAE值均小于其他几种模型的预测误差，可以证明stacking组合模型在工作日的预测上也具有有效性和一定的精确性。从图3a、图3b可以看出,虽然组合模型预测的MAE值最小,但在拟合曲线上还有一定的误差,一些峰值和波动特征没有预测出来。火车东站不同于一般的工作区、生活区或者娱乐区的地铁站点,火车东站地铁站客流受到火车站的影响较大,进出站客流在有一定程度上表现得更加随机,所以模型在预测上没有长周期的数据支持,很难做到精确的预测。

3 结束语

本文从轨道交通换乘站客流的波动和随机性出发,考虑邻近数据和异常值对于组合模型的影响,提出了一种基于stacking算法的GGRK-MLR组合预测模型。组合预测模型利用MLP神经网络对于输入数据权重的更新迭代,结合梯度提升回归和随机森林回归对于客流数据特征的强大学习能力以及对于异常值的敏感性,在此基础上加入K近邻回归模型,进一步提高组合模型对于邻近数据的拟合能力。实验结果表明,在时间粒度为5 min时,GGRK-MLR组合预测模型能够较好的预测大型综合车站的短期进出站客流,且相对于GBR、RFR、KNN、MLR具有更好的预测精度。但是,模型仅仅考虑提取客流数据的时间特性,没有进一步挖掘天气因素、站点土地利用性质以及站点客流之间的相互影响。这也是本文的下一步研究方向,即增加空间特性的影响因素,建立泛化性能鲁棒性以及预测精度更高的组合预测模型。