一种基于广域角速度信号的暂态励磁控制方法

杨冬锋，孙 智，刘迎迎

(1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学)，吉林 吉林 132012；2.国网潍坊市寒亭区供电公司，山东 潍坊 261100)

随着大量发电机组的并网运行，各区域电网互联，特别是交直流混联电网的初步形成，使得我国电网结构愈加复杂，导致电力系统受到干扰的情况也愈加复杂[1-3].当电网发生大干扰时，其稳定性受到严重威胁，通过对发电机的励磁系统进行控制可以从“源头”处消除电网的不稳定因素，并且控制的效益/投资之比很高，因此励磁控制凭借其经济性和有效性成为提高系统暂态稳定性的首要手段[4].

文献[5]提出了暂态励磁强增控制技术，其为开环控制并且基于远端的直流闭锁信号来控制，自适应能力差，可靠性不够.文献[6]首先提出了暂态稳定全过程励磁控制策略，此方法主要基于本地信号进行控制，无法通过全局监测准确识别需进行控制的发电机，导致系统稳定性恶化.随着广域测量系统的发展对系统进行全局监测成为了可能，文献[7]提出了一种基于广域测量系统的发电机强励控制技术，此技术将广域信号与本地信号相结合的方式对发电机进行控制，其控制器主要基于系统等值功角曲线摆动进行控制，但实际系统中等值功角信号很难获取，因此实际控制难度较大.

本文提出了一种将广域信号作为控制器输入的励磁控制方法.首先当系统受到大扰动后，识别系统内的临界机群，然后通过设计好的控制器对临界机群内所有发电机进行励磁控制，最后通过Matlab/Simulink仿真平台搭建10机39节点经典模型验证本文提出的励磁控制方法可以改善电力系统暂态稳定性.

1 临界机群识别

多机系统中，故障后各发电机受扰程度不同，系统内同调性不同的机群间发生相对运动，其相对运动情况随着时间变化而变化[8].根据EEAC理论，在受到扰动后，多机系统中的所有发电机组可以分为两群：临界机群和其余机群.临界机群识别是电力系统暂态稳定控制的重要步骤[9-10]，准确识别出临界机群与暂态稳定控制方法直接相关[11-12].

1.1 发电机组转子运动过程

正常运行的电力系统中，施加于发电机转子上的机械力矩和电磁力矩处于动态平衡状态，从而使发电机转子匀速旋转[1].当系统发生大扰动时，发电机的电磁力矩降低，但机械转矩不变，导致发电机转子加速运转.发电机功角δ和角速度ω能充分显示转子运动过程，发电机运动方程为

(1)

公式中：Δω=ω-ω0，Δδ=δ-δ0，Δf=f-f0，Δω为角速度变化量；Δδ为功角变化量；Δf为频率变化量；TSΔδ为阻尼转矩；TSΔω为同步转矩；ω0为工频下系统同步角速度；δ0为稳态下发电机初始功角；f0为工频50 Hz；ω为发电机瞬时角速度；δ为发电机瞬时功角；f为系统瞬时频率.

1.2 临界机群识别判据

在不同情况下临界机群识别方法不同，本文采用以下判据：

(1)当电力系统发生故障后，系统内几台发电机相对参考发电机失去稳定即系统失稳情况下：首先设系统内惯量时间常数最大的一台发电机为平衡机并将其作为参考机组，然后通过观察所有发电机相对参考机组的功角曲线进行临界机群识别，即相对功角曲线发散的发电机可构成临界机群，其余发电机构成其余机群.

(2)当电力系统发生故障后，系统内所有发电机组均能通过自动调节趋于新的稳定情况下：首先根据相对功角曲线识别出受扰最严重的一台发电机，然后识别出与受扰最严重的发电机具有同调性的发电机组，受扰最严重的发电机和与其具有同调性的发电机构成临界机群.同调机群通过功角和角速度进行识别，具体方法如下：

具体设受扰最严重机组为Gj，若发电机Gi满足公式(2)，则认为Gi属于临界机群：

(2)

公式中：Δδi(t)=δi(t)-δi0，Δδj(t)=δj(t)-δj0，Δωij(t)=Δωi(t)-Δωj(t)，Δωi(t)=ωi(t)-ω0，Δωj(t)=ωj(t)-ω0，σ1和σ2分别为两台发电机功角差阈值和角速度差阈值；设|Δδij(t)|的最大值为Δδijmax即为两机在整个研究时段内的最大相对功角变化量.设|Δωij(t)|的最大值为Δωijmax即为两机在研究时段内的最大相对转速变化量.

2 基于广域信号的暂态励磁控制

对于暂态稳定，励磁控制可以从“源头”抑制不稳定状况的扩散；并且电力系统对各发电机配置励磁控制器，使其互相作为后备，进而提高系统紧急情况下的稳定性.因此，发电机励磁控制由于其很高的效益/投资之比成为提高电力系统暂态稳定性的首选控制方法.暂态励磁控制可以在一定时间内强行将励磁电压提高到顶值充分发挥励磁控制改善电力系统暂态功角稳定性的作用.在励磁控制过程中，合理地设计励磁控制器是改善暂态稳定的保障.本文通过李雅普诺夫理论推导出利用广域测量信号作为控制器输入信号全局性地进行励磁控制，以更加准确地改善系统暂态稳定性.

2.1 暂态励磁控制原理

各发电机在系统惯量中心(Center of Inertia，COI)坐标下的等值转子角δCOI和等值角速度ωCOI为[2]

(3)

公式中：δi和ωi分别为第i台发电机转子角和第i台发电机角速度与同步角速度偏差值，Mi为第i台发电机惯性时间常数.

EEAC法分析假定系统失稳为双机模式，其中受扰严重的发电机组构成临界机群(简称S机群)，剩余的发电机组构成其余机群(简称A机群).双机等值时，惯量中心S机群和A机群运动方程为

(4)

公式中：δS和δA分别为临界机群和其余机群的等值转子角；MS和MA分别为临界机群和其余机群内各发电机惯性时间常数总和；PmiS和PeiS分别为临界机群内第i台发电机的机械功率和电磁功率；PmjA和PejA分别为其余集群内第j台发电机的机械功率和电磁功率.

上述双机等值系统可进一步简化为单机无穷大系统，表示为

(5)

其中：

(6)

公式中：M、δ、Pm和Pe分别为单机无穷大系统的等值惯性时间常数、转子角、机械功率和电磁功率.

发电机的电磁功率与其机端电压成正比，因此可通过提高发电机机端电压增大其电磁功率，而励磁控制是性价比最高的提高机端电压的方法.一般情况，机械功率需要通过原动机进行调节，因此其控制过程复杂.所以只能通过调节电磁功率进行控制，若提高其余机群内发电机的电磁功率Pej则系统总电磁功率降低，系统的制动转矩减小，使系统暂态稳定性恶化；若提高临界机群内发电机的电磁功率Pei则系统总电磁功率升高，系统的制动转矩增大，可以改善系统暂态稳定性.由上述可知，仅对临界机群内发电机进行励磁控制才能改善系统稳定性.

2.2 基于广域信号的励磁控制器设计

李雅普诺夫理论可用来推导励磁控制策略改善系统暂态稳定性[13].给定非线性动态系统有dx/dt=f(x)，对于未施加控制的系统在平衡点x0处于稳定状态，可定义李雅普诺夫函数变量V(x)，李雅普诺夫稳定判据为[14]

(7)

未施加控制的系统能量函数为

(8)

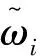
公式(8)中能量函数导数为0，即

(9)

dV/dt=dVunctrl/dt+dVctrl/dt，

(10)

当受控部分即dVctrl/dt≤0时，可改善系统的暂态稳定性.

当含有励磁控制的系统发生故障后，励磁电压由系统不受控部分产生的励磁电压(上标为0)和强励电压组成，表示为

(11)

故障后机端电压E′i与励磁电压成正比关系，即

E′i=K·EfdiE′i=E′0i+ΔE′i，

(12)

公式中：E′0i为故障后未受控制部分产生的机端电压；ΔE′i为故障后励磁控制产生的机端电压.

系统发生故障后能量函数的导数可表示为

(13)

Sentinel Haus，德国一家对室内空气质量进行测试的组织，报道了一项研究项目，该项目涉及在实验室内建造的两个小型儿童教室。第一次使用常规材料，第二次使用的只是Sentinel Haus认可的产品。在常规教室中，在第1周测量的是5 000 μg/m3的TVOC水平，在第4周减少到2 800 μg/m3，并在8周时降至2 700 μg/m3。德国环境保护署建议，长期暴露下的TVOC水平不超过1 000μg/m3。 使用获得批准产品建成的教室，TVOC水平不得超过500 μg/m3。

将ΔPi和ΔCij带入公式(13)可得

(14)

(15)

广域励磁控制器控制框图，如图1所示.

从图1可知：Eref为机端参考电压；Et为机端电压；Ep为电力系统稳定器输出信号；ω为角速度；ωCOI为系统惯量中心的等值角速度；ΔEB为广域励磁控制施加的附加励磁电压；Ef为励磁电压.

控制器逻辑为

3 算例仿真分析

本文通过在Matlab/simulink仿真平台搭建经典10机39节点系统模型验证所提励磁控制方法的可

行性.

经典10机39节点系统中包括10台发电机组如图2所示，39个母线节点，12条含变压器线路，34条普通线路.节点1至节点29为PQ节点，节点30至节点38为PV节点，节点39为平衡节点，发电机G1为参考发电机.因此在线路L21-22靠近节点22处的变压器高压侧设置三相短路，当t=1 s时故障发生并在t=1.24 s故障切除.系统中各发电机相对参考发电机G1的相对功角曲线，如图3所示.

由图3可知，发电机G6、G7相对参考发电机的功角曲线发散因此失去稳定，所以通过临界机群识别判据可判定G6、G7构成临界机群，其余发电机构成其余机群.

本文通过李雅普诺夫理论推导出由本地角速度信号和广域角速度信号结合作为控制器的输入信号进行励磁控制，且系统中的角速度信号比功角信号更易获取，控制方便.当系统发生上述故障后，通过对识别出的临界机群内的所有发电机组G6和G7安装的励磁控制器对其进行控制.控制过程中，控制器的输入角速度信号，如图4所示.

图3 不施加控制时各发电机相对功角曲线图4 G6、G7和惯量中心角速度

图4所示为控制器的输入信号，并且控制策略为

(1)在首摆过程中，当ωG6-ωCOI>λ和ωG7-ωCOI>λ时,分别启动安装在发电机G6和G7的励磁控制器；

(2)在首摆过程中，当ωG6-ωCOI<λ和ωG7-ωCOI<λ时，分别将发电机G6和G7的励磁控制器退出运行.

通过上述控制策略进行控制后，根据图5可知，当对临界机群内所有发电机进行本文所提出的基于广域角速度的励磁控制方法进行控制时，失去稳定的系统可在励磁控制下趋于稳定，明显提升了系统的暂态稳定裕度，改善了系统稳定性，验证了本文所提出励磁控制方法的有效性.

4 结 论

针对电网故障后的暂态稳定问题，本文研究了基

于广域角速度信号的励磁控制方法.可得如下结论：

(1)文中通过李雅普诺夫理论推导出将本地角速度信号和广域角速度信号相结合作为励磁控制信号的暂态励磁方法.由于系统中的角速度信号比功角信号更容易获取，因此该方法在工程中更简单易行；并且广域信号为全局信号，使得该控制方法对系统的整体动态变化更敏感，控制效果更好.

(2)通过仿真算例对失去稳定的10机39节点系统应用本文提出的励磁方法进行控制后可使失去稳定系统趋于稳定，明显提升了系统的暂态稳定裕度，验证了该方法的可行性.