一种雷达主瓣复合干扰盲源分离对抗方法

李 军, 高 乾, 王 欢

(1.空军工程大学， 陕西西安 710051； 2.空军通信士官学校， 辽宁大连 116600)

0 引言

针对雷达的跟踪环节，自卫式干扰通常释放拖引干扰与压制干扰的复合干扰，以达到“隐真示假”的干扰目的[1]。这种情况下，早期的前沿跟踪、距离保护波门、宽波门跟踪、记忆波门跟踪等波门跟踪策略将失效。现有的大多数基于目标和干扰幅度特征差异的干扰检测方法[2-3]、利用空时自适应和极化处理进行干扰抑制方法[4]以及其他一些信号或数据处理的干扰抑制方法[5]，都没有充分地考虑复合干扰情况。并且，由于干扰与目标回波来自同一角度，雷达接收到的是单通道信号，传统正定或者超定盲源分离算法将失效。针对上述问题，本文提出了一种极化通道扩展与盲源分离相结合的干扰抑制新方法。先通过极化通道扩展将单通道信号扩展为双通道信号，再利用盲源分离算法分离目标与干扰，可以对真、假目标同时跟踪处理，而不会丢失真目标。

1 复合拖引干扰建模

假设拖引干扰为jd(t)，具有压制效果的干扰信号为jb(t)，则自卫式复合拖引干扰可以表示为

j(t)=jd(t)+ηjb(t)

(1)

式中：jb(t)可以为噪声调频干扰、噪声卷积/乘积干扰等；η表示jd(t)和jb(t)能量分配关系，η越大压制效果越明显；拖引干扰jd(t)信号形式与雷达发射信号有关。

雷达工作于PD体制时，jd(t)通常为距离-速度同步拖引干扰。因为现代PD雷达兼具距离和速度测量能力，可以同时获得目标的距离-速度二维信息，因此单独的距离或者速度波门拖引干扰对其干扰效果有限。不失一般性，假设PD雷达发射单载频相干脉冲串信号，其信号模型可以表示如下：

(2)

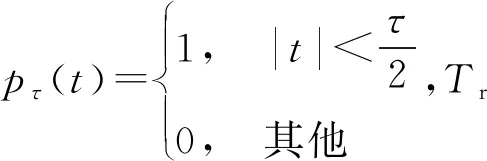
DRFM干扰机距离-速度同步拖引干扰的过程为：首先，对接收到的雷达发射信号进行下变频得到基带信号；然后，对基带信号进行相位量化、模数转换并存储；最后，对存储在DRFM中的信号进行延时调制c(t)和多普勒频率调制b(t)后进行上变频并转发，形成对雷达的距离-速度同步拖引干扰，干扰模型可以表示为

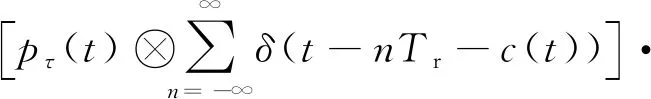
ej2π(f0+fd+b(t))(t-c(t))

(3)

式中，fd为目标多普勒频率，c(t)为距离拖引时延函数，b(t)为同步施加的多普勒频率调制。实际应用中，距离拖引通常在几秒时间内拖动几个距离波门(μs量级)，因此，在一个PD雷达相关处理间隔(CPI)内，c(t)通常远小于Tr，可以用δ(t-nTr)代替式(3)中δ(t-nTr-c(t))，则干扰模型简化为

ej2π(f0+fd+b(t))(t-c(t))

(4)

2 极化通道扩展建模

自卫式复合拖引干扰条件下，雷达只能接收到一路信号。雷达辅助天线主要用于相干旁瓣对消，为了消除主辅通道交叉极化响应不匹配的影响，通常采用垂直和水平两种辅助天线对消掉干扰信号的垂直和水平分量。可以利用与主天线极化方式正交的辅助天线接收信号，构建第2路混叠信号，得到进入主、辅天线接收信号vm(t),va(t)：

(5)

(6)

式中：hm为雷达主天线的极化矢量；ha为交叉极化辅助天线的极化矢量；er(t)，ej(t)分别为在雷达接收天线端口处的目标回波信号和干扰信号，可分别表示为

er(t)=SphmArs(t)

(7)

ej(t)=hjAjj(t)

(8)

式中，Sp为目标的极化散射矩阵，hj为干扰机发射天线的极化矢量，Ar和Aj分别为雷达接收到的目标回波以及干扰信号的幅度。根据雷达方程和干扰方程，有

(9)

(10)

式中，Pt为雷达发射信号的峰值功率，gm为雷达主天线增益，λ为雷达工作波长，σ为目标RCS，R为目标与雷达的距离。

考虑通道噪声N，根据式(5)～(8)，可以得到雷达主、辅接收通道信号的向量-矩阵表达式：

Y=AS+N

(11)

式中，

(12)

(13)

(14)

3 极化通道扩展盲分离算法

3.1 算法的数学模型

设目标回波为sr(t)，干扰j(t)，则在雷达接收天线端口处，主天线和交叉极化辅助天线的接收信号可分别表示为

(15)

(16)

进入雷达主、辅接收通道的信号可以表示为

(17)

表示成矩阵形式，即为V=AS+n。

下面根据盲源分离的3个基本假设讨论回波信号和干扰信号的可分离性：

1) 源信号间相互统计独立。目标回波和干扰是由两个相互独立的物理过程所产生，可以认为两者是统计独立的。

2) 混合矩阵列满秩。干扰机为了避免极化失配通常将天线设计为斜极化或者圆极化，而目标通常具有较为复杂的外形，其极化散射矩阵随着视角的变化而变化，即在接收天线端口处，回波信号和干扰信号具有不同的极化状态，又由于辅助通道采用正交极化，因而混合矩阵A为列满秩矩阵。

3) 至多含有一个高斯分布的源信号。目标回波和复合拖引干扰中，至少目标回波信号为非高斯分布信号。

假设一个P×P阶矩阵M，则以M为特征矩阵，可构造y的四阶累积量矩阵：

(18)

式中，y为白化后的观测向量，yi,yj,yk,yl分别为y的第i,j,k,l个元素，vij表示矩阵Vy(M)的第i行第j列元素，mlk表示矩阵M的第l行第k列元素。

结合独立分量分析(ICA)及高斯噪声高阶累积量为零的性质，将式(18)变换为

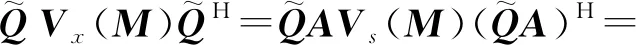
UVs(M)UH

(19)

由白化矩阵的特点可知，U为酉矩阵。同时，由于源信号是相互独立的，上式中四阶累积量矩阵Vs(M)为对角矩阵，有

Vy(M)=UΛUH

(20)

构造c-FastICA盲分离算法的代价函数模型为

J(w)=E{G(|wHY|2)}

(21)

式中，Y为白化后观测信号，w∈CN为分离矩阵某一列，满足约束条件w=1。

因此，c-FastICA的最优化问题可以表示成如下形式：

(22)

基于牛顿法，可以推导出c-FastICA算法的不动点迭代公式为[6-8]

w(m+1)=-E{g(|z|2)(z)*Y}+

E{g′(|z|2)|z|2+g(|z|2)}w(m)

(23)

式中，z=w(m)HY，m为迭代次数，g为G的一阶导数，g′为G的二阶导数。

3.2 计算机仿真结果

仿真实验参数如表1所示，选择噪声调频和噪声乘积干扰作为压制式干扰，噪声乘积干扰的调制噪声为零均值、方差为1的高斯白噪声。

表1 仿真实验设定参数

根据表中参数可以计算得到拖引率为α=β/Tc≈10-6，为了达到同步拖引效果，施加多普勒频率应为fdj=2αf0=19.31 kHz。假设目标回波幅度为1，JSR=20 dB，SNR=10 dB，图1～图2仿真了雷达接收到目标+复合拖引干扰的时域及频域波形。

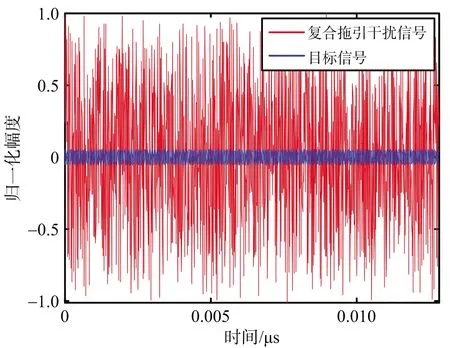
(a) 时域波形

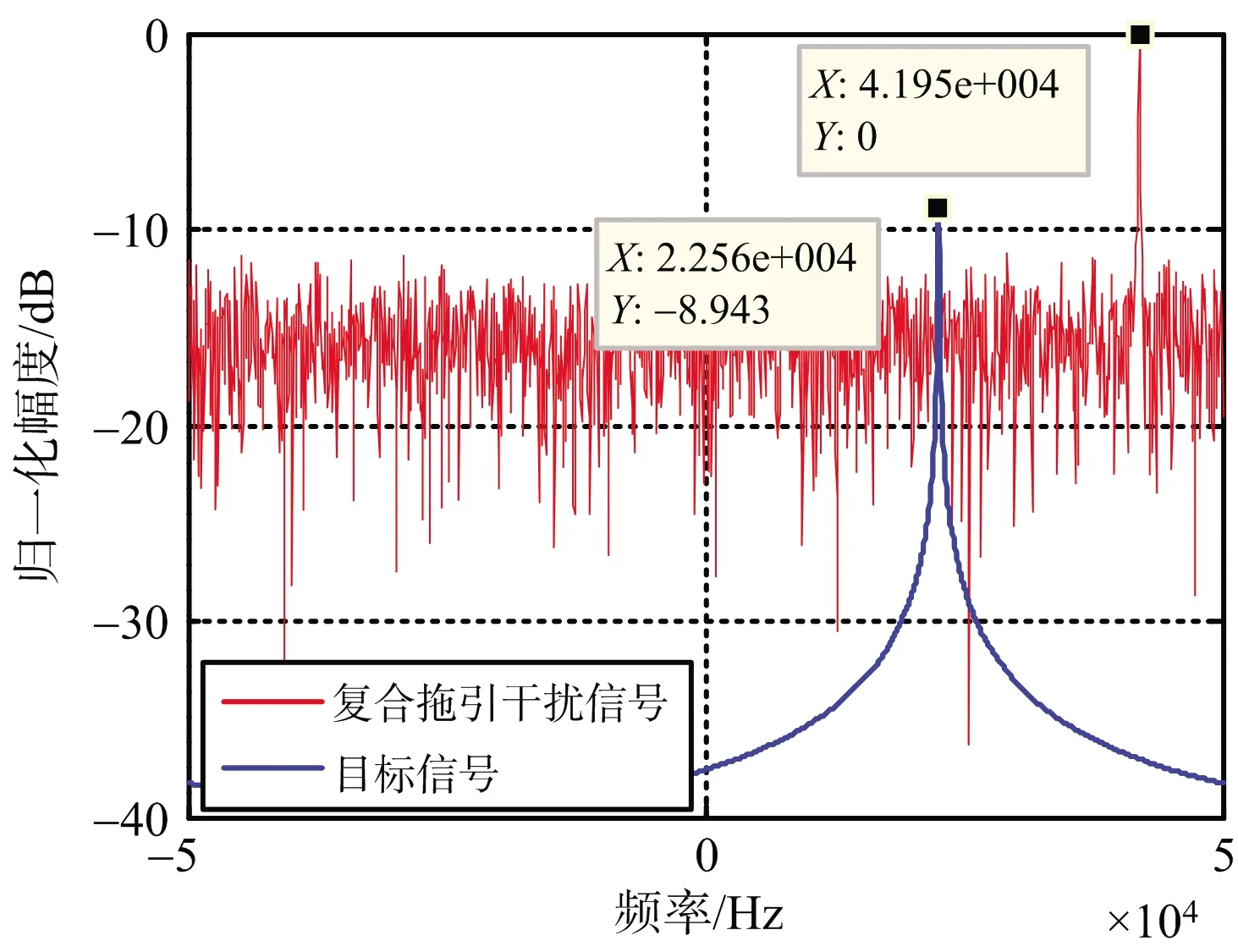
(b) 频域波形

(a) 时域波形

(b) 频域波形

由图1(b)和图2(b)可以看出，真、假目标的多普勒频率相差约19.39 kHz，与理论值基本一致，误差是计算机量化造成的。利用极化通道扩展和盲源分离算法，可以得到两路分离的信号， 图3～图4分别仿真了两路分离信号的幅频分布。

由图3～图4可以看出，在两种针对PD雷达的拖引复合干扰条件下，利用提出的极化通道扩展和盲源分离算法可以很好地将干扰与目标回波分离开，进而能够利用分离出来的两路信号完成对目标和干扰的同时跟踪处理。

(a) 第1路分离信号

(b) 第2路分离信号

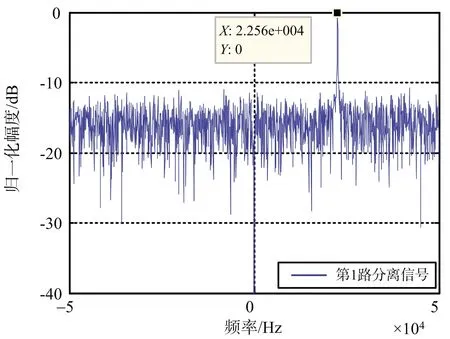
(a) 第1路分离信号

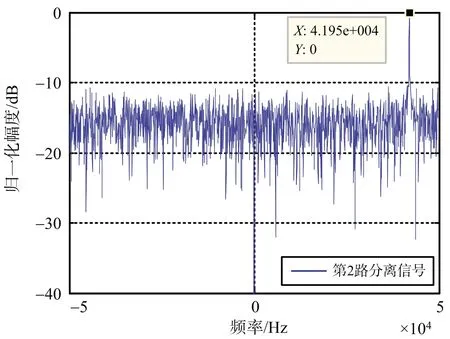
(b) 第2路分离信号

4 结束语

为了对抗现代干扰机释放的复合拖引干扰，本文首先建立了复合拖引干扰的模型，并采用极化通道扩展的方法弥补了单通道处理时需做欠定盲源分离的缺陷，在此基础上提出了一种基于极化通道扩展和BSS的干扰抑制方法，并针对“噪声调频+距离-速度拖引复合干扰”和“噪声乘积+距离-速度拖引复合干扰”两种情况进行了分析，理论推导和仿真结果表明，所提出的算法在两种典型的复合拖引干扰情况下可以较好地分离目标和干扰。