基于金属橡胶和介电泳效应的微粒循环过滤实验研究

宋春磊, 任玉坤,2,*, 何文俊, 姜天一, 姜洪源,*

(1. 哈尔滨工业大学 机电工程学院, 哈尔滨 150001; 2. 哈尔滨工业大学 机器人技术与系统国家重点实验室, 哈尔滨 150001)

0 引 言

金属橡胶是一种弹性多孔材料(将螺旋形态的金属丝堆叠后以冷冲压工艺成形)，既具有所选金属的固有特性，又拥有橡胶一样的弹性，故而得名[1-2]，现已广泛应用于各种环境下的减振[3]、节流[4]和过滤[5]等。与其他多孔过滤材料相比，金属橡胶具有特殊优势[2, 5-6]：金属橡胶孔隙度高，过滤寿命长；由于具有弹性，可以根据应力改变其孔隙度，从而实现过滤精度的调节，即过滤性能可调。但是，仅依靠金属橡胶的多孔特性实现微米级颗粒的过滤非常困难，颗粒尺寸限制了金属橡胶的应用范围。

微尺度范围的颗粒操纵有着广泛的应用，如工厂机器废油中金属微屑的过滤、污水中细小颗粒的分离等。目前，已经有多种操纵微粒的方法，如诱导电荷电渗[7-9]、介电泳(Dielectrophoresis, DEP)[10-12]、离心处理[13]、声波分离[14]以及磁场[15]等。与其他方法相比，介电泳易于实现且已得到广泛应用，只需施加非均匀的交流电信号即可轻松操作，不需额外设备或组件，也不要求颗粒的介电性与生物标记性[16]。

近年的研究表明，利用介电泳操纵粒子，可以实现多种功能。Hunt等[17]提出了一种基于介电泳效应的电泳钳，可用于捕获单个细胞。Song等[18]介绍了一种连续流动调控的微流控装置，通过横向位移偏转和交流电场的开/闭来控制粒子运动轨迹。Han等[19]提出了一种浓缩技术，利用负介电泳将颗粒捕获于连续移动的液滴一侧，之后分裂液滴，从而提高母液滴中的粒子浓度。目前，介电泳主要用于粒子的分离与收集，而在粒子过滤方面则缺乏相关研究。

本文通过液态金属驱动的电毛细流动实现自循环泵送，研究金属橡胶材料过滤微粒的特性。首先，使用Galinstan液态金属产生连续的电毛细流动以稳定地泵送电解液，在有限空间内实现流体自循环运动[20-22]；然后，对多孔金属橡胶板施加交流电信号，产生介电泳力，整体上看，介电泳力与流体对粒子的Stokes力相反，从而使粒子停留于金属橡胶板周围，达到过滤目的；最后，通过对比实验和数值模拟结果，讨论交流电信号幅值UAC、流速uL等参数对过滤效率的影响。

1 芯片结构

在过滤实验中，微粒的运动与电解液的自循环流动一致。电毛细应力作用在位于石墨电极对中心的Galinstan金属液滴表面，产生单向自循环流动。当石墨电极对上施加直流电信号后，在一定尺寸的圆柱形腔体限制下，液滴运动会始终保持在腔体内。此外，为消除泵送与过滤时施加的两个外部电场之间的相互干扰，将过滤区域与液态金属座腔设置于对侧，使二者距离最远，如图1(a)中的1和4。采用经典的模塑法将PDMS浇铸在图1(b)所示的PMMA模板上，固化脱模后得到高为3 mm的芯片通道，将其与玻璃基板键合，得到微流控芯片(图1(c))。实验使用的金属橡胶材料为0Cr18Ni9Ti，线径为80 μm，尺寸为14 mm×8 mm×2 mm，如图1(d)所示。

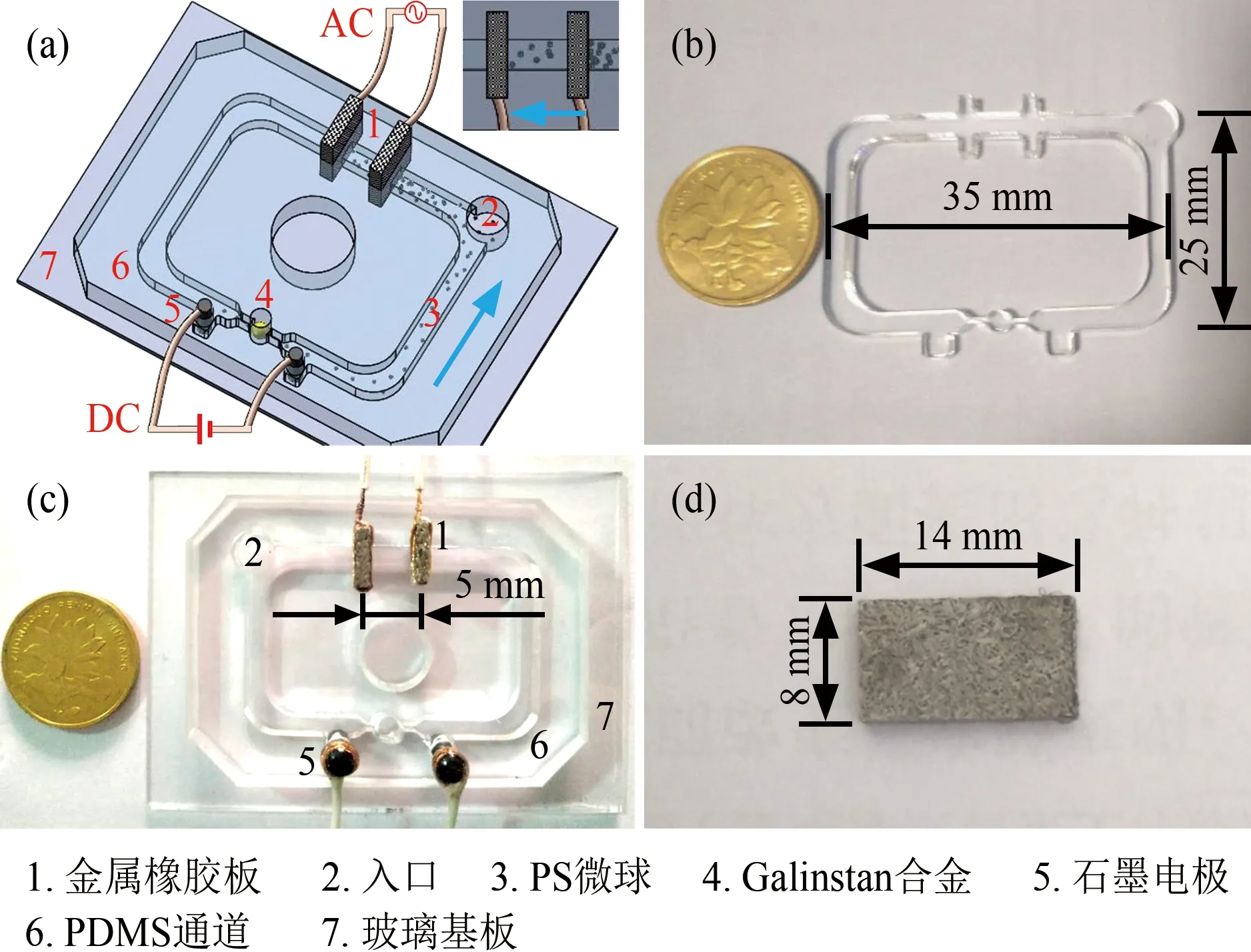
图1 过滤芯片通道结构

金属橡胶板具有高度连通的活性孔隙，可根据使用要求设计加工为不同的孔隙度，孔隙度P通常定义为[5]：

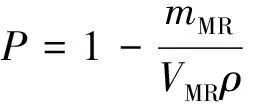
(1)

式中，mMR为构成金属橡胶的金属丝的质量，VMR为金属橡胶的体积，ρ为金属丝的密度。

进一步推导出金属橡胶的平均孔隙φ为：

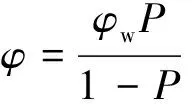
(2)

式中，φw为金属丝的线径。经计算，实验采用的金属橡胶板的孔隙度P=0.3571，平均孔隙约为40 μm。

2 数值计算方法

2.1 介电泳效应

采用数值计算方法分析了介电泳对过滤性能的影响。介电泳是指当粒子与电解液的极化率存在差异时，粒子发生极化，在表面诱导出束缚电荷，从而在非均匀电场中沿着电场梯度方向运动的现象。当粒子极化率大于电解液极化率时，将沿着梯度升高的方向运动，介电泳力为正(positive DEP, pDEP)，反之则为负(negative DEP, nDEP)。通过CM因子fCM来衡量其极化特性[10-12]：

(3)

在本文计算模型中，电解液为σf=0.5 S/m、εf=73ε0的NaOH溶液(ε0为真空介电常数)；粒子为σp=4×10-4S/m、εp=2.5ε0、r=5 μm的聚苯乙烯微球。施加的交流电信号频率恒为1 MHz，此时CM因子的实部Re[fCM]=-0.5，因此在金属橡胶板周围，粒子受到负介电泳力的作用。

在交流电场中，通常考虑时均介电泳力〈FDEP〉：

〈FDEP〉=πεfr3Re[fCM]|E2|

(4)

式中，“〈 〉”表示时均，E为电场强度。

为更加直观地分析介电泳效应的影响，将时均介电泳力转化为粒子的速度。根据Stokes定律，聚苯乙烯微球的介电泳速度uDEP为：

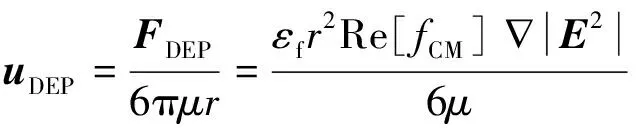
(5)

式中，水溶液的动力黏度μ=1×10-3Pa·s。

2.2 物理模型的简化

采用有限元分析软件Comsol Multiphysics 5.3进行数值模拟。金属橡胶内部结构十分复杂，在建模时需要根据其平均孔隙进行简化，将其截面视为40 μm×40 μm阵列分布的均匀多孔介质[2]，如图2所示。微通道整体结构的网格数量过于庞大，且计算意义不大，因此仅对粒子过滤区域及其附近通道进行计算，取过滤区域尺寸为20 mm×3 mm×3 mm，其中，单个金属橡胶板的轴向长度为2 mm。

图2 数值仿真的几何模型

对金属橡胶板施加频率为1 MHz、幅值不同的交流电信号，在过滤区域产生电场梯度。为便于分析，通过在过滤模型中施加流入流量，等效地处理了对侧通道中液态金属诱导极化引起的电毛细流动泵送现象(图2中右侧为入口)。

3 结果分析

3.1 数值模拟结果

对不同的金属橡胶板间距D、交流电信号幅值UAC和流速uL条件下的过滤效率以及电热效应进行了数值模拟。

图3对比了金属橡胶板间距D对过滤效率的影响。在交流电信号幅值UAC=200 V、流速uL=25 μm/s(方向从右至左)条件下，对比分析了不同时刻粒子在过滤区域的分布情况。可以看出，随着间距增加，流经第一层过滤区域的粒子数量增多，过滤效率降低。这是因为间距D与电场强度E成反比，而FDEP∝|E|2，因此间距增加使介电泳力减小，通过过滤区域的粒子数量增加，降低了过滤效率。

图3 不同金属橡胶板间距时粒子过滤的数值模拟结果

Fig.3 Numerical simulation results of particle filtration at different spacings

但是，在高电导率(σ≥0.1 S/m)电解液中，施加大的交流电信号，会产生焦耳热，通道内的流体会产生较强的交流电热效应，电极附近区域的流体发生快速流动(如图4所示，uET为交流电热效应在金属橡胶附近引起的流动速度)，形成涡流，从而影响粒子过滤。在选择合适间距的多次实验中发现，当间距为3 和4 mm时，在金属橡胶板两侧会产生比较显著的电热效应，影响粒子过滤；当间距为5 mm时，电热效应影响减弱，能够实现粒子过滤。

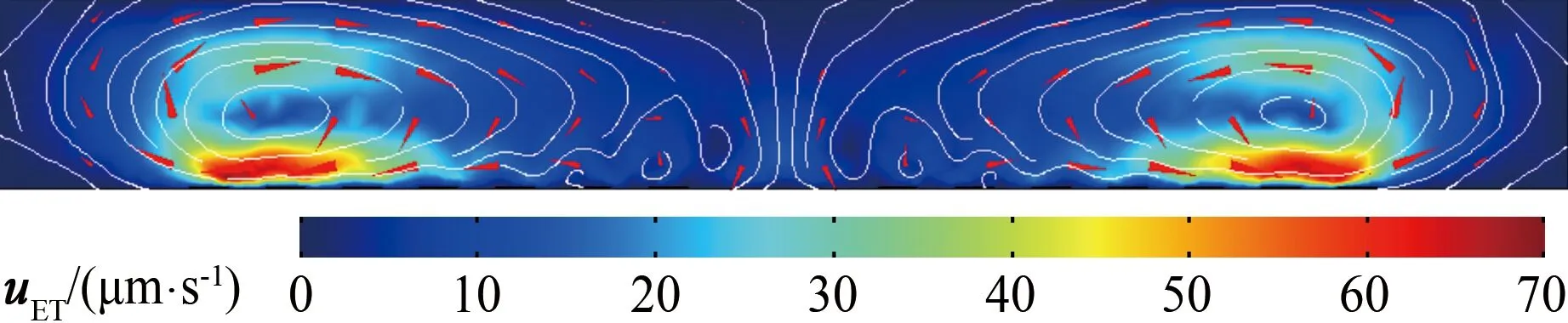
图4 通道内流体的交流电热现象

图5对比了交流电信号幅值UAC对过滤效率的影响(金属橡胶板间距D=5mm、流速uL=25 μm/s)。不难发现，结合介电泳效应可以提高过滤效率，且施加的交流电信号幅值越大，粒子受到的介电泳力越大，即〈FDEP〉∝|E|2，过滤效率越高。因此，在条件允许的前提下，应当尽量使用较高的交流电信号幅值。

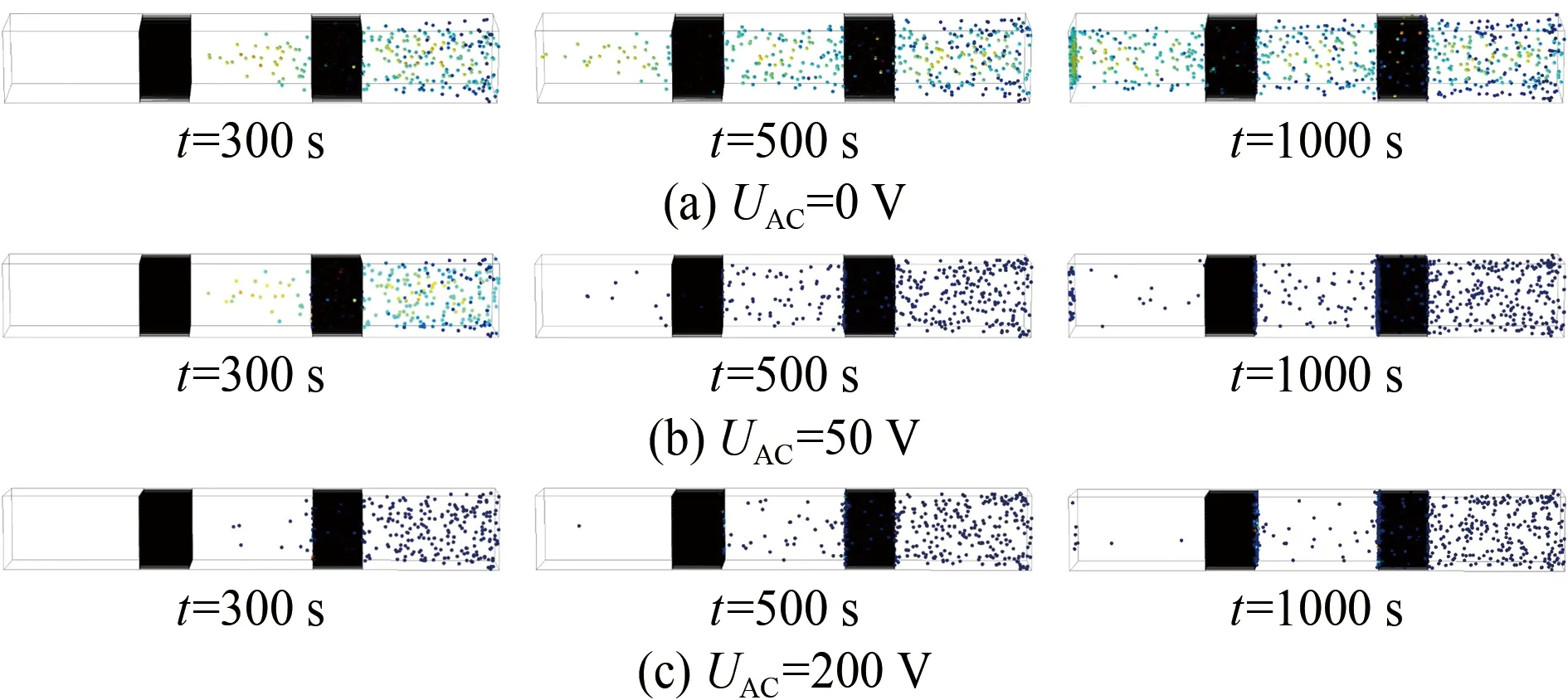
图5 不同交流电信号幅值时粒子过滤的数值模拟结果

图6对比了流速uL对过滤效率的影响。当交流电信号幅值为200 V时，计算得到|E2|≈6.5×1014V2/m3，粒子的介电泳速度uDEP=126 μm/s。随着流速增加，介电泳力的主导作用逐渐减弱，流经过滤区域的粒子数量增加，过滤效率降低。

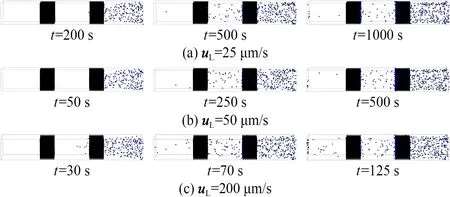
图6 不同流速时粒子过滤的数值模拟结果

Fig.6 Numerical simulation results of particle filtration at different flow rates

3.2 未施加交流电信号时的过滤特性

结合以上数值模拟结果，使用图1(c)所示的芯片进行了实验研究(金属橡胶板间距D=5 mm)。实验中，采用微观粒子图像测速技术(Micro-PIV)从连续图像帧中获取示踪粒子的运动速度以表征流速uL。测量系统包括倒置荧光显微镜(CKX41，Olympus，物镜放大倍率10×，NA=0.25)、CCD相机(Prime BSI，Teledyne)等。已知图像尺寸为2 mm×2 mm，CCD分辨率为2046 pixel×2046 pixel，考虑各种误差，取图像空间分辨率为1 μm。采用图像处理软件ImageJ 4.0进行互相关分析计算流速，经多次计算取平均值。

图7展示了未施加交流电信号、流速uL=48和238 μm/s时过滤前后的实验结果，左、中、右图分别为过滤前、第一层过滤和第二层过滤状态，黑点为聚苯乙烯微球。对实验现象进行分析，统计多块相同矩形面积(366 μm×366 μm)内的粒子数，绘制出过滤前后粒子数和过滤效率随时间变化的曲线，如图8所示。粒子过滤效率ηp通过下式计算：

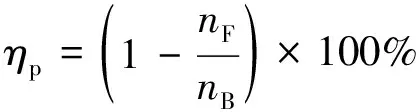
(6)

式中，nB、nF分别为过滤前后的粒子数。

在图8(a)中，时间达到15 min后，过滤前后的粒子数变化很小。这是因为通道较长，短时间内携带大量粒子的流体无法到达过滤区域，在15 min后粒子过滤效率才达到稳定值。显然，仅依靠金属橡胶板的间隙无法实现对5 μm粒子的有效过滤，这一点在图8(b)中更为明显，可以看出，粒子的稳定过滤效率最大不超过15%，这可能是由于架桥效应或静电吸附造成粒子堵塞从而实现了过滤。

3.3 施加交流电信号后的过滤特性

在金属橡胶板上施加幅值为200 V、频率为1 MHz的交流电信号，在不同流速条件下进行粒子过滤实验,图9展示了流速uL=100和51 μm/s时过滤前后的实验结果。随着流速降低，介电泳力对粒子的驱动逐渐占据主导作用，过滤效率提高。

图7 未施加交流电信号时过滤前后通道中粒子数的变化

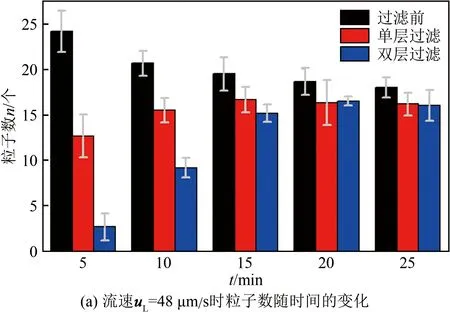
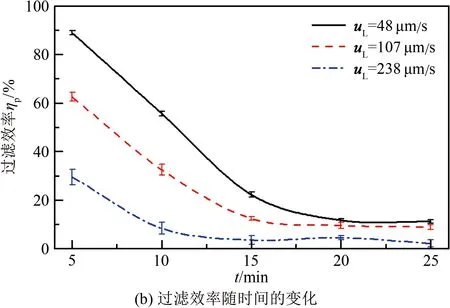
图8 未施加交流电信号时粒子数与过滤效率随时间的变化趋势

Fig.8 Variance of particles number and filtration efficiency with time when no AC signal is applied

图9 施加交流电信号时过滤前后通道中粒子数的变化

图10给出了加电后粒子数与过滤效率随时间的变化趋势，进一步对比了单层与双层结构的过滤效率。从图10(a)不难发现，在较短时间内，粒子运动距离过短，因此在过滤区域后出现的粒子数较少，过滤前后的粒子数变化比较明显。当时间达到15 min后，过滤区域前后的粒子数变化不明显，说明粒子过滤效率达到了稳定值。

图10(b)中流速uL=51 μm/s时粒子过滤效率随时间的变化曲线，对应于图10(a)单层过滤的粒子数变化。可以看出，当流速增加后，过滤效率明显降低，当流速达到245 μm/s时，稳定过滤效率已不足10%，这一结果与图8(b)中uL=238 μm/s时的结果偏差不大，这是因为此时的流速uL远超过介电泳速度uDEP，起主导作用的为流速。

对比图10(b)与(c)可以发现：当流速相同时，单层结构的稳定过滤效率低于双层结构，其最大稳定过滤效率低于60%；当流速高于200 μm/s，单层结构和双层结构的稳定过滤效率相差不大(差值小于10%)。因此，在能够有效实现过滤时(过滤效率不低于50%)，流速uL不应超过介电泳速度uDEP的80%(流速低于100 μm/s)，此时通过提高过滤结构的层数，可以大大提高过滤能力。

由式(5)可知，uDEP∝r2，粒子的介电泳速度与粒径r关系很大，通常要求r>1 μm[10-11, 16]。当r<1 μm时，粒子受到的介电泳力较弱，此时不能实现粒子的有效过滤；随着粒径增大，由于较强的介电泳力和有限的平均孔隙，能够实现更高的过滤效率。

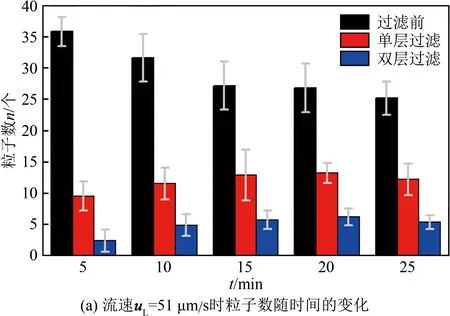
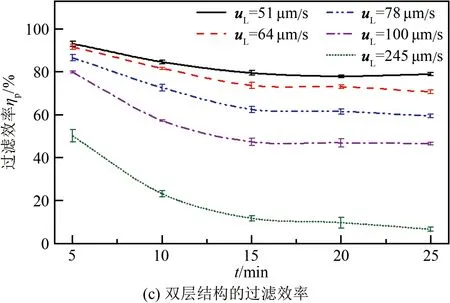
图10 施加交流电信号时粒子数与过滤效率随时间的变化趋势

Fig.10 Variance of particles number and filtration efficiency with time when AC signal is applied

4 结 论

本文开发了一种微流控装置，将直流电场感应的液态金属液滴的电毛细单向循环泵送流动和交流电场驱动的多孔金属橡胶板附近的负介电泳力结合，提高了金属橡胶板对微粒的过滤能力。

(1) 无介电泳力作用时，仅依靠金属橡胶板自身孔隙无法实现对5 μm聚苯乙烯微球的有效过滤。

(2) 在实验条件下，当流速低于60 μm/s时，双层结构的稳定过滤效率可达80%以上，而单层过滤结构的稳定过滤效率接近60%。无论是单层结构还是双层结构，流速对金属橡胶板的过滤效率都有较大影响，应控制其不超过介电泳速度的80%。