基于Excel的遗传算法在大学生数学建模中的应用

颜清，苗壮，徐调斌，蒋昌猛，赖鑫生

(上饶师范学院 数学与计算机科学学院，江西 上饶 334001)

遗传算法在工程优化和工业控制等领域得到广泛应用。吴立华等针对某机械的悬臂结构采用遗传算法进行优化设计,有较快的收敛速度和很高的计算精度,建立了单目标非线性优化设计数学模型,为多目标非线性结构优化设计提供了强有力的方法和工具[1]。李月引入免疫算法来改进遗传算法,在TSP应用中解决种群迭代次数过多的复杂问题中,经过疫苗检验和退火选择降低算法的退化概率,避免了种群的退化现象[2]。播种机的播种质量、播种效率和能耗由于受播种地形和地域的影响不能发挥到最佳状态，秦华等提出了一种基于BTO模式的多目标速度控制遗传算法优化模型，确定了BTO模式下播种机性能优化的初始参数，明显的改善了播种机的播种质量、播种效率和播种能耗，提高了播种机的作业性能[3]。针对基本遗传算法存在收敛速度慢、早熟等不足,王雷等提出了一种改进自适应遗传算法，根据进化过程中个体适应度值的大小自动调节交叉概率和变异概率,使算法能够跳出局部最优解,移动机器人路径规划的仿真实验表明，改进的遗传算法有效可行，明显提高了机器人路径规划的质量[4]。每年的大学生数学建模竞赛中遗传算法也用于解决数学建模中的优化问题。刘兆仁等利用遗传算法对公共自行车如何在各大中型城市高效调度建立了VRP模型,采用标准算例针对算法进行检验,结果表明遗传算法能够有效求解自行车的调度模型[5]。根据“立竿见影”和竿影日照图的原理，于鹏等提出了一种太阳影子定位方法。他们首先结合太阳高度角、太阳赤纬角，以理论影长和实际影长的相关系数最大和其误差平方和最小为目标函数建立了求太阳影子定位的多目标优化模型，采用遗传算法进行求解，求解结果无论在精度还是在收敛速度上都优于传统的枚举算法[6]。在每年一届的大学生数学建模教学及指导中，如何让大学生在一段较短时间内较快地掌握遗传算法是一较为棘手的问题。笔者将遗传算法嵌入在Excel中，利用Excel表格功能、函数功能及VBA混合编程对遗传算法的优化过程进行仿真，模拟遗传算法的选择、交叉和变异三个基本操作，充分展现了遗传算法解决大学生数学建模中优化命题的魅力，获得了较为满意的应用效果，解决了大学生数学建模中的优化问题。

1 遗传算法的VBA优化仿真概述

遗传算法即模拟自然界生物群体一代一代的繁衍进化，通过迭代操作，产生新一代较优的个体作为问题的解，如同生物群体一代一代不断繁衍、进化，最后收敛到最适合生存环境的一代生物个体，即为问题的最优解。问题解的优劣通常用适宜度表达，适宜度即表示为生物群体不断繁衍中个体对生存环境适宜性的强弱程度，适宜度大的个体被选择为繁衍下一代父代的概率就大，其染色体就会在一个甚至多个下一代的基因中出现，这种有选择性的将最优染色体进入下一代的繁衍行为，表现出达尔文物择竞天、适者生存、优胜劣汰的自然界生存法则，这种最优选择策略在遗传算法中起到决定性作用。

所谓的遗传算法VBA优化仿真，即在Excel表格中用一组单元格中的{0，1}二进制串表示遗传算法中的一个“染色体”个体，再由Excel表格功能自动仿真计算“染色体”个体的环境“适宜度”，由此再通过竞争在表格中产生更适应环境的新一代仿真“染色体”个体群，一个新一代“染色体”个体即为问题的一个可行解。通过Excel表格功能与VBA混合编程，在Excel表格中生动地模拟出“染色体”的竞争过程：“染色体”个体基因如何被选择、复制进入下一代，如何通过交叉、变异过程产生更适应环境的新一代“染色体”个体群等，如此通过一代一代进化，最终收敛到最适应环境的最新一代的“染色体”个体群，从而获得问题的最优解等过程。

2 算法过程仿真

以下通过函数f(x)=11sin(6x)+7cos(5x)为例，在数据处理的常用软件Excel中，通过Excel的表格功能、函数功能及与自带的VBA混合编程，即利用Excel遗传算法求函数在x∈[0,2π]区间中最大值，阐述Excel遗传算法的优化仿真过程。

2.1 Excel遗传算法VBA优化仿真过程

2.1.1 遗传算法的初始群体

求解的精度决定“染色体”个体的{0，1}二进制串长度。设定求解精度x为四位小数，须将0到2π区间分为6.283 2×104等分，编码的二进制串至少需要16位，即32 768=215<6.283 2×104<216=65 536，即Excel遗传算法通过16个连续单元格中的“0”或“1”的二进制串作为“染色体”个体的遗传编码。20个“染色体”的群即由20行、每行16个“0”或“1”的连续单元格即可表示。利用Excel的自动计算功能，在“染色体”个体的{0，1}二进制串之后的单元格，可以分别对“染色体”个体的“十进制值”“实际x值”“函数f(x)值”进行仿真计算[7]。

2.1.2 初始群体适宜值的计算与遗传选择

由于f(x)在x∈[0,2π]区间上有正有负，以20个“染色体”群中最大的正数与最小的负数之间的区间为1，“染色体”群中最大的正数其“区间值”为1，最小的负数其“区间值”为0。根据适者生存的生物遗传法则，以函数值f(x)的“区间值”作为适宜值，将“染色体”群中“染色体”个体的“区间值”累加，个体的“区间值”占“区间值”总和的百分比值就是“染色体”遗传进入下一代的概率。根据个体的“区间值”的百分比值设计成轮盘赌(图1)，每个个体的这个百分比值即为“轮盘比例”，在轮盘赌上根据“染色体”顺序划定确定的区域，适宜值高的“染色体”个体在轮盘赌上占有的区域就大，被选择的机会就高，充分体现了适者生存的生物遗传法则。

图1即为初始群的Excel遗传算法仿真计算表。图中轮盘赌的仿真数值区域在0-1之间，刻度值与时钟的0点至12点分度对应，通过随机函数每次选择一个0-1之间的随机数，确定选择轮盘赌对应区间的“染色体”，可以看出适宜度高的“染色体”由于其“轮盘比例”大而被多次选择，一些适宜值低的“染色体”在轮盘赌中对应区间小而难以选择而被淘汰。适宜度最低的11号“染色体”的“轮盘比例”值为0，直接淘汰。图1所示，由于函数f(x)的值为“适宜值”，16号“染色体”的“适宜度”最大，“轮盘比例”达9.63%，选择次数也最多，20次的选择中，被选择了3次，即16号“染色体”的基因复制了3次进入下一代“染色体”中，占比达15%；17号“染色体”的“适宜度”较大，仅次于16号“染色体”，“轮盘比例”为9.27%，也被选择了3次。第1、3、4、5、7、9、11、18、20号“染色体”，平均“适宜度”占比小于2.61%，20次的选择中，选择次数均为零。注意到，图1中最后两列的“选择值”数据列仅对应于前列的选择序号n列，其它各列对应行数据为各“染色体”个体对应数据。

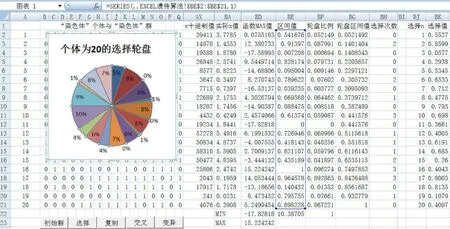
图1 遗传算法的选择与轮盘赌

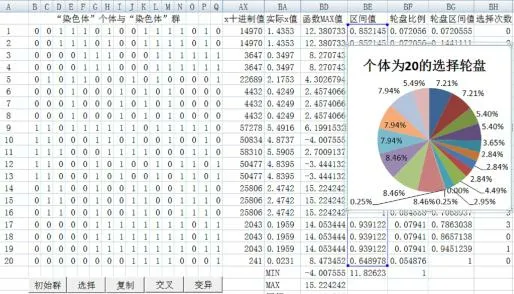
图2 遗传算法的复制与仿真计算

2.2 遗传算法VBA优化仿真混合编程

2.2.1 选择、复制确定下一代“染色体”基因

图1、图2是依次执行“初始群”“选择”和“复制”三按钮中的VBA代码的仿真计算结果。经轮盘赌选择后，通过Excel混合编程进行复制。遗传复制遵循“优胜劣汰”的自然遗传法则，可以看出,许多“染色体”在遗传复制时未被选择，淘汰率达45%。图1与图2的仿真计算显示，个体的“适宜值”大入选概率就大，“适宜值”小的如第3、5、7、9、11、18号“染色体”，“适宜值”占比小于1.35%均被淘汰。如下为VBA混合编程完成复制操作的程序代码。

L=0'将选择的“染色体”{0，1}二进制串由“Excel遗传算法”表复制到“Excel遗传算法1”表

For i=1 To 20

m=Sheets(“Excel遗传算法”).Cells(i + 1, 60)

If m=0 Then GoTo 10

For n=1 To m

For j=1 To 16

Sheets(“Excel遗传算法1”).Cells(L + 2, j + 1) = Sheets(“Excel遗传算法”).Cells(i+1, j+1)

Next j

L=L+1

Next n

10 Next i

被选择的“染色体”由“Excel遗传算法1”表转移回“Excel遗传算法”表后完成选择、复制

For i=1 To 20

For j=1 To 16

Sheets(“Excel遗传算法”).Cells(i+1, j+1)=Sheets(“Excel遗传算法1”).Cells(i+1, j+1)

Next j

Next i

从VBA程序代码中看出，轮盘赌选择确定了新一代“染色体”的基因，根据“初始染色体群”表(图1)中的BH列列出对应序号的仿真“染色体”个体的选择次数进行复制，得到第二代“染色体”群的基因(图2)，其平均“适宜值”比“初始染色体群”要高出许多，整个算法的选择、复制仿真过程跃然纸上。

2.2.2 交叉、变异产生新一代“染色体”个体

图3为第七代“染色体”群经选择、复制后的仿真图，图4为经配对完成交叉操作后的“染色体”群的仿真图。对照图3图4可以看出，交叉配对产生了更为优秀的个体，交叉配对前“染色体”个体“适宜值”最高为17.582 882，交叉配对后“染色体”个体“适宜值”最高为17.595 591，未选取交叉配对的3对即1、11，7、17，8、18等三对个体经变异后竞争进入下一代“染色体”群。更为可喜的是交叉配对前最优秀的五个“染色体”个体，其中4个“染色体”经交叉操作“适宜值”得到进一步提高，未变的一个“染色体”原因是未交叉直接进入，由此可见，交叉配对产生的新个体使优秀“染色体”进一步优化。

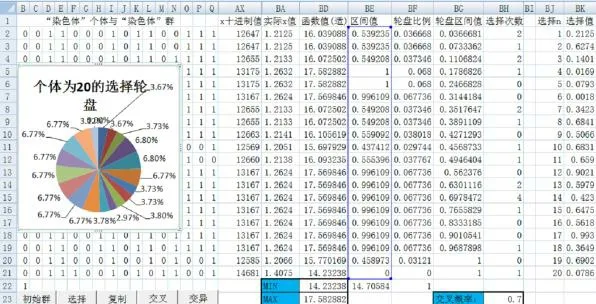
图3 新一代个体的选择与复制

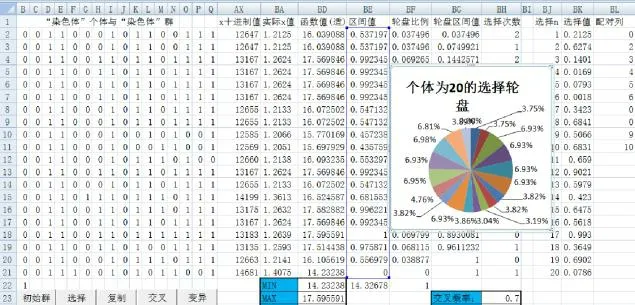
图4 交叉、变异产生新一代个体仿真图

变异概率确定为0.01，即100个长度的{0，1}二进制串中，随机抽取一个进行变异，群体的{0，1}二进制串累计为320位，共有3.2个二进制位变异，即3个或4个二进制位变异。变异是一个较小的扰动，只对“染色体”群带来较小的改变。

历经选择、交叉、变异等三个算子作用后，下一代仿真“染色体”群宣告诞生。结合表格计算功能的VBA混合编程可以形象地让学生了解遗传算法的基本思想。

2.3 遗传算法VBA优化仿真的终止条件

遗传算法的终止条件通常设为两类：(1)最大遗传代数的设定；(2)种群中基因多样性测度。两个终止条件通常会结合起来运用，若将最大遗传代数的设定为100代，在不到100代时，计算种群中基因多样性测度，若所有基因位相似程度急骤上升，此时收敛于概率为1的优良个体，遗传算法即可终止。

3 遗传算法VBA优化仿真的应用

3.1 遗传算法VBA优化仿真辅助数学建模教学

大学生数学建模与优化问题联系非常密切，遗传算法解决大学生数学建模优化问题是较重要途径。大学生学习遗传算法VBA优化仿真，很容易掌握遗传算法的基本思想，熟悉选择、交叉、变异等基本算子的作用，在辅助大学生数学建模及相关教学中得到应用。

3.1.1 算法过程的仿真及其可视化

在遗传算法VBA优化仿真过程中，以Excel表格数据及图形的形式揭示“染色体”在遗传过程中的演变规律，利用Excel混合编程完成遗传算法基本算子的操作，实现遗传算法演化过程的可视化。

3.1.2 “染色体”个体的仿真

在Excel表格中，利用一组16个连续单元格表示的{0，1}二进制串，作为仿真“染色体”个体的遗传算法编码。如{0，1}二进制串“1001000101011001”，十进制数为37 209，若用以表示x为0至6.283 2中的数，即x=0+37 209×6.283 2/(216-1)=3.567 4，f(x)的绝对值为9.798 081 7，都可以通过Excel表格直接计算得到这些结果，使算法过程直觉化、可视化，“染色体”个体仿真加深了大学生算法学习的感性认识。

3.1.3 选择算子中轮盘赌的仿真

根据各“染色体”适宜值设计轮盘赌，配上插图就很直观。图1中看出整个轮盘赌的数值区域在0-1之间，通过随机函数每次选择一个0-1之间的随机数，就可以确定每次是哪个“染色体”被选择，也可以看出适宜值高的“染色体”往往被多次选择并遗传至下一代，有些适宜值低的“染色体”很难被选择而淘汰。

3.1.4 交叉操作的可视化

选择操作只是完成了产生新一代“染色体”群的第一步，接着就是交叉、变异操作。大学生可以直接从仿真表格中(图1)看出，前面最优秀的5个“染色体”个体，其中4个“染色体”经交叉“适宜值”得到进一步提高。大学生通过对照交叉前后的“染色体”，变化一目了然。由于交叉概率选择0.7，即只有70%的“染色体”进行交叉配对，20个“染色体”个体中有14个“染色体”个体要进行交叉配对，最优秀的5个“染色体”个体有一个“染色体”未交叉配对直接进入新一代“染色体”群。由此可见，交叉配对产生的新个体使优秀“染色体”进一步得到优化。图5、图6是1至60代中“染色体”群中最优“染色体”与“染色体”平均适宜度的仿真计算结果，60代时，最优解为17.833 39，与答案17.833 99相差极小。

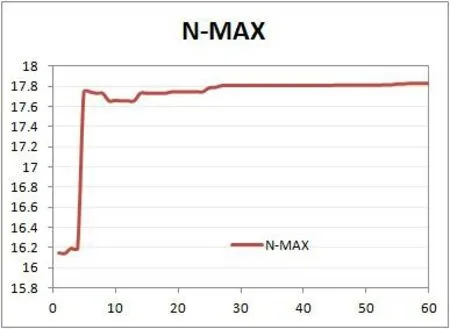
图5 1至60代中的最优“染色体” 图6 1至60代“染色体”平均适宜度

3.1.5 变异操作方法的多样性

变异操作是一个较小的扰动，对“染色体”群带来较小的改变。通过变异操作，打开了新的搜索空间，容易找出“染色体”个体{0，1}二进制串中已经变化的几个位置。历经选择、交叉、变异等三个算子作用后，下一代“染色体”群宣告诞生，很明显，大学生对这一过程心领神会，遗传算法的VBA优化仿真在课堂上以过程仿真的形式讲授提升了教学效果。

3.2 遗传算法VBA优化仿真与数学建模

课堂上遗传算法的VBA优化仿真形象、生动，学生容易理解，但要掌握遗传算法的VBA优化仿真在大学生数学建模中解决优化命题还需要学生实践操作，最为实用例子是选择以往大学生数学建模中的优化选题。

3.2.1 应用于适应度的变化

对于函数f(x)= 11sin(6x)+ 7cos(5x)，可以在x∈[0,2π]区间上对函数求最大值，也可以对函数求最小值，这就只要在适应度列中作适当改变就行。如求最小值，即在适应度列的每行加负号即可。若函数f(x)改变了，且变量只有一个，也只要改变“适应度”列(对应“轮盘比例”列)的各行。

3.2.2 应用于求解精度与变量个数的变化

遗传算法的VBA优化仿真程序在“染色体”个体与“染色体”群所对应的列(图1)中预留了32列。如要改变求解精度，可以对“染色体”个体与“染色体”群所对应的列进行增减。f(x) 函数关系改变，“染色体”个体与“染色体”群所对应的列有48列，适应有3个以内变量且求解精度为10-4的f(x)函数。

3.2.3 应用时克服轮盘赌的缺点

轮盘赌还与“赌”字有关，如图1中所示，1、4、20号个体的“适宜度”达到5.00%以上未被选择，而“适宜度”占比仅4.19%的15号个体被选择2次，这也是它的缺点所在。因此，为避免最优基因的流失，通常加入最优基因保留技术。

3.2.4 避免早熟与局部寻优问题的思考

遗传算法VBA优化仿真也可一代一代操作，也可连续操作直接得到结果。辅助教学时，往往采用一代一代操作，学生能清楚地了解算法的过程细节。初始群局限了最优解的搜索空间[8]，一代一代操作容易发现遗传算法的早熟与陷入局部寻优等问题，通过对操作的调整，如选择较好的初始群就可避免早熟与局部寻优。变异操作确保了新一代基因的多样性，打开了新的搜索空间，可以看出扩大搜索空间影响收敛速度，故变异概率常取1%或以下。

4 结束语

在Excel表格中形象地完成遗传算法的选择、交叉、变异的过程仿真，将Excel表格自动计算功能与VBA编程相结合，算法过程形象地呈现在学生面前。在Excel表格中操作遗传算法，Excel算法过程的可视化与实时动态仿真效果，使大学生对算法的原理、过程、算子、适宜度等基本要点了解得非常透彻，使大学生在数学建模中应用遗传算法的VBA优化仿真得心应手，挥洒自如，为遗传算法在运用时进行适当改进打开了思路[9]，为解决数学建模中优化命题提供了崭新的解决方案。