基于悬链线的斜拉索垂度效应等效弹性模量计算方法

赵海霞，张文明，蒋晓放，刘钊

(1.南京航空航天大学 金城学院，江苏 南京 211156；2.东南大学 土木工程学院)

1 前言

斜拉桥是一种受力合理、造型美观的桥型，近60年来得到了迅猛发展。中国2008年建成的苏通大桥(主跨1 088 m)将斜拉桥跨径首次突破千米大关，同年中国香港建成了主跨1 018 m的昂船洲大桥，2012年俄罗斯建成了主跨1 104 m的俄罗斯岛大桥。中国目前正在施工的沪通长江大桥(主跨1 092 m)是目前世界最大跨度的公铁两用斜拉桥，也是世界首座跨度超过千米的公铁两用桥梁。

随着斜拉桥跨度的增大，斜拉索的长度及水平投影长度也随之增大。上述4座斜拉桥的最长斜拉索长度分别为581、540、580和576 m，最长斜拉索的水平投影长度分别为533、450、483和544 m。现代斜拉桥多采用密索体系，斜拉索的安全系数不小于2.5，因此成桥状态斜拉索应力水平不高，一般小于700 MPa。在施工期内，新安装的斜拉索应力水平往往更低。斜拉索超长的水平投影及低应力水平导致其垂度效应明显。斜拉索垂度的大小与索力有关，垂度与索力呈非线性关系。斜拉索张拉时，索的伸长量包括弹性伸长以及克服垂度所带来的伸长，为了方便计算，可以用等效弹性模量的方法，在弹性伸长公式中计入垂度的影响。1965年，Ernst基于斜拉索抛物线线形推导出等效割线模量公式，考虑了拉索初始应力和拉索应力刚化现象，得到了广泛应用；洪显诚和Hajdin分别于1992年和1998年推导出了既计入垂直于拉索的自重分量又考虑平行于拉索自重分量作用的等效弹性模量公式，对Ernst公式进行了修正。为了解决使用Ernst公式时可能出现的索拉力与拉伸量之间关系的不闭合问题，2000年李国平提出了斜拉索非线性分析的状态修正法；之后，国内外学者开始了基于拉索的悬链线线形研究垂度引起的几何非线性问题。2001年夏桂云等推导了斜拉索的等效刚度表达式，该公式把拉索水平分力作为输入变量之一，这一点与Ernst公式不一致；2009年Vairo提出了一个改进的精细割线等效弹性模量公式，2012年又计入了温度效应的影响。为了简化推导过程，他们均使用了小垂度假定，认为拉索水平分力与轴力之比为拉索两端点连线倾角的余弦值。2015年王立彬等引入损伤程度、范围和位置3个参数，以弧坐标作为基本变量推导出损伤拉索静力分析的基本模型，但没有给出等效弹性模量的具体表达式。

该文基于悬链线线形，首先建立斜拉索等效弹性模量的数值算法；然后摒弃小垂度假定推导出等效弹性模量的简化公式，利用斜拉索上端点的轴向拉力作为输入变量之一，与Ernst公式一致，方便使用。

2 Ernst公式

常用的Ernst公式可表达为：

(1)

式中：Eeq为斜拉索的等效弹性模量；Ee为钢丝的弹性模量；γ为钢丝重度；l0为水平投影长度；σ为应力，σ=T/A；T为上端点的轴向拉力；A为横截面面积。

3 斜拉索悬链线线形和基本参数

图1所示斜拉索，其悬链线线形的微分方程为：

(2)

式中：q为斜拉索单位长度自重；H0为水平拉力。

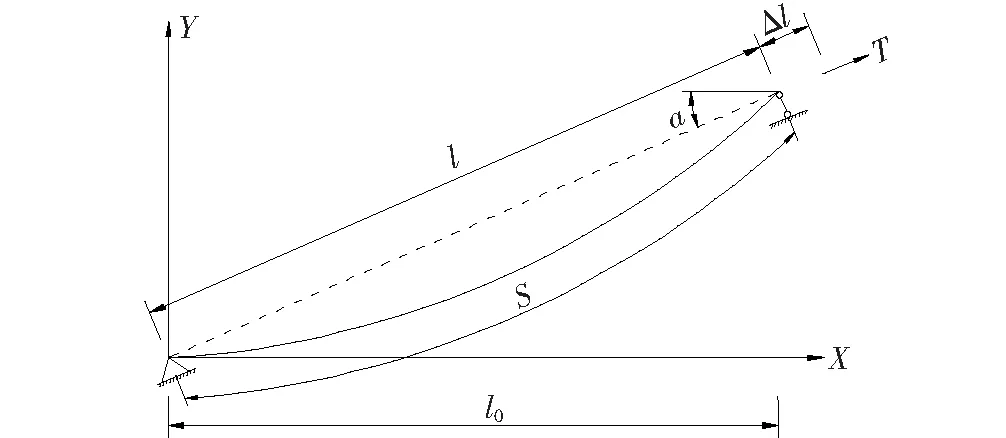
图1 斜拉索的线形和基本参数

求解微分方程(2)，并引入适当的边界条件，可获得悬链线方程为：

(3)

利用悬链线方程进行积分，可获得斜拉索的长度S为：

(4)

斜拉索上端点的轴向拉力T可表示为：

(5)

跨中垂度f可表示为：

(6)

4 斜拉索等效弹性模量计算方法

基于悬链线线形，首先建立斜拉索轴向拉力与克服垂度的伸长量之间的关系，获得垂度效应的当量弹性模量；然后与斜拉索钢丝的弹性模量进行合并，可获得斜拉索的等效弹性模量,即：

(7)

式中：εe为斜拉索弹性应变；εf为斜拉索克服垂度引起的伸长对应的当量应变；Ef为垂度效应的当量弹性模量。

用弹性模量的概念表示斜拉索垂度的影响，则Ef可表示为：

(8)

其中：

Δl=S-l

(9)

式中：Δl为斜拉索垂度引起的索长；l为斜拉索上下两端点之间的距离。

关于垂度效应的当量弹性模量Ef的计算，该文提出两种计算方法：数值算法和简化公式算法。

4.1 数值算法

(10)

将式(10)代入式(8)即可求出当量弹性模量Ef，然后代入式(7)即可求出斜拉索等效弹性模量Eeq，具体计算流程如图2所示。该方法用到的公式没有经过简化，只要计算时H0的增幅足够小，其结果就趋近于精确解。

然而，对于已知拉索上端轴向拉力T或拉索应力σ的情形，即类似于Ernst公式的已知条件，该方法应用起来不太方便，因此有必要提出简化公式算法。

4.2 简化公式算法

基本思路：将λ表示成T的函数，代入Δl的表达式，从而将Δl表示成T的函数，最后对T求导。

将coshλ表达为麦克劳林级数展开式，取前5项近似得：

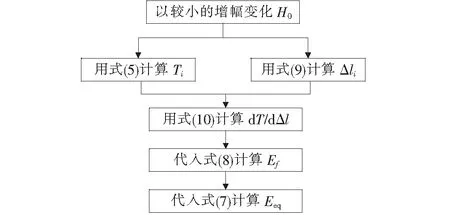
图2 基于非弹性悬链线理论的数值算法计算流程

(11)

代入式(4)，可得：

(12)

代入式(9)，可得：

(13)

在式(5)中，可令：

(14)

其中：

(15)

代入式(14)，可得：

(16)

又有：

(17)

将式(16)、(17)代入式(5)，可得：

(18)

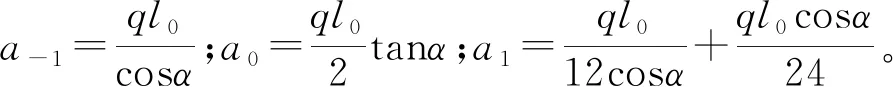
由式(18)可得：

a1λ2+(a0-T)λ+a-1=0

(19)

解之，得：

(20)

代入式(13)，得：

(21)

对T求导，可得：

(22)

(23)

5 线密度变化的影响

上述计算是基于“无弹性悬链线理论”，即索变形前后的单位长度重量不变。然而，当索力很大时，索变形前后的单位长度重量变化较明显。为了研究线密度变化对等效弹性模量的影响，该节基于“弹性悬链线理论”建立等效弹性模量的求解算法。

索受力伸长之后单位长度重量变化为：

(24)

(25)

重新计算与q1有关的下列参数：

(26)

(27)

(28)

(29)

基于弹性悬链线理论的斜拉索长度和上端点的轴向拉力可分别表示为：

(30)

(31)

6 工程算例

沪通长江大桥斜拉索单位长度重度q=7 644 N/m，横截面面积A=0.078 m2，水平投影长度l0=544 m，钢丝弹性模量Ee=205 GPa，两个端点连线的倾角α=19.29°。 利用该文提出的数值算法和简化公式算法计算等效弹性模量，如表1所示。在数值算法中，水平力H0的增幅为50 kN，不足H0的0.5%。从表1可以看出：两种理论算出的结果很接近，说明索线密度变化对等效弹性模量的影响非常小。

将该文算法的结果(无弹性悬链线理论)与Ernst公式计算结果在表2中进行比较。

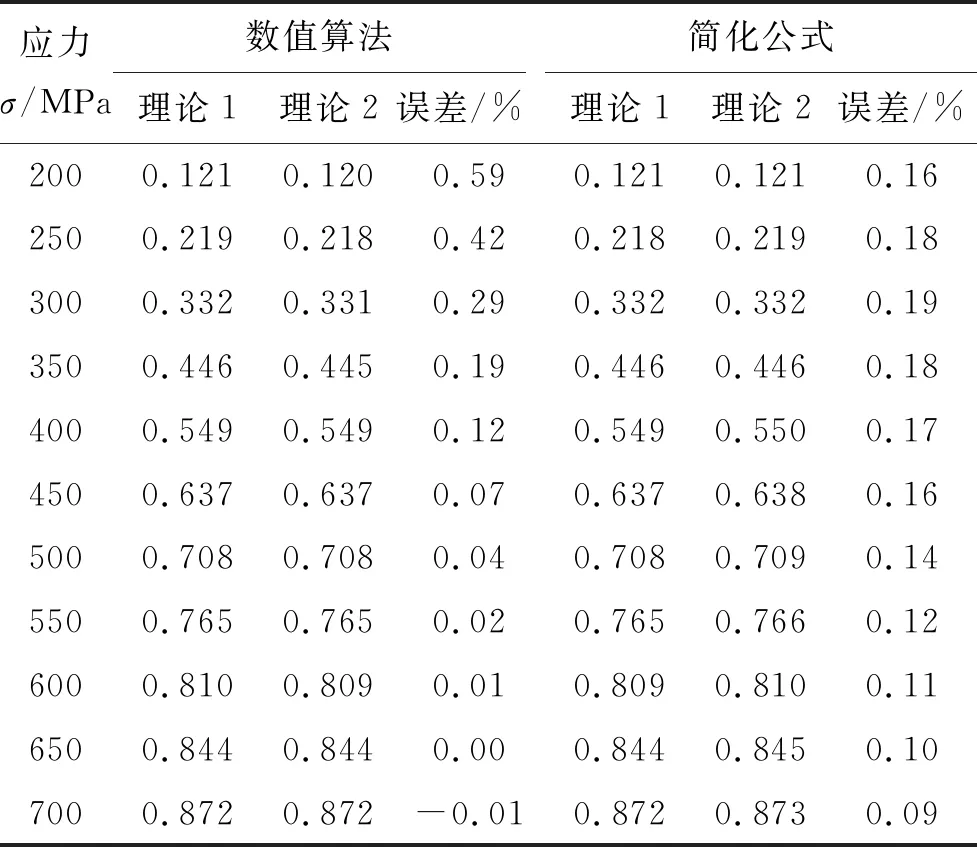
表1 该文方法、简化公式计算的等效弹性模量(Eeq/Ee)

注：理论1、2分别为无弹性悬链线理论、弹性悬链线理论。

表2 斜拉索等效弹性模量计算结果

如果把斜拉索水平投影长度l0也作为变量，可计算获得等效弹性模量Eeq随l0的变化曲线，如图3所示。

图3 Eeq与l0的关系

从图3可以看出：① 在变化趋势方面，该文公式与Ernst公式基本一致，再次证明了该文方法的正确性；② 等效弹性模量Eeq随l0的增大而减小，因此对于大跨度斜拉桥的超长索，垂度效应导致刚度显著折减。

7 结论

该文基于斜拉索的真实线形建立了考虑垂度效应的等效弹性模量的数值算法和简化公式，并采用沪通长江大桥最长斜拉索作为算例，对比分析了该文方法与传统Ernst公式的计算精度，得到以下结论：

(1) 在高应力水平下，该文方法与Ernst公式计算结果非常接近；在等效弹性模量Eeq随水平投影长度l0变化的趋势上，该文方法与Ernst公式基本一致。证明了该文方法的正确性。

(2) Ernst公式对于低应力水平的斜拉索精度不高，如应力为200 MPa时，误差高达17.29%；随着应力的增大，误差逐渐减小到1%以内。

(3) 该文的简化公式算法误差不超过0.3%，精度高于Ernst公式，适合推广应用。

(4) Ernst公式计算结果高于数值解，而该文的简化公式计算结果略低于数值解。

(5) 由于垂度效应的影响，等效弹性模量Eeq小于钢丝弹性模量Ee，Eeq/Ee的值随斜拉索应力水平的增大而增大。

(6) 等效弹性模量Eeq随水平投影长度l0的增大而减小，因此对于大跨度斜拉桥的超长索，垂度效应导致刚度显著折减。

(7) 索受力前后线密度的变化对等效弹性模量的影响很小，可忽略不计。