基于能量原理的曲线连续刚构桥抗震性能分析

刘建威，罗文博，李德建

(1.中南大学 土木工程学院，湖南 长沙 410075；2.长沙市规划设计院有限责任公司；3.湖南省交通规划勘察设计院有限公司)

曲线连续刚构桥近些年正朝着更大跨径、更小曲率半径和更高墩高的方向发展，跨径、墩高、曲率半径等对抗震性能的影响也是连续刚构桥抗震性能分析的研究方向。既有文献对大跨连续刚构桥的抗震研究多集中在强度破坏和变形破坏，较少从能量角度出发进行抗震性能分析。该文从损伤与能量两方面对连续刚构桥进行抗震性能参数分析。

1 工程概况

平舟河大桥跨径布置为(81+150+81) m，曲率半径为1 500 m。上部构造尺寸如图1、2所示，柱墩为双肢薄壁墩，承台为矩形承台。

图1 墩顶梁截面构造图(单位：cm)

图2 跨中梁截面构造图(单位：cm)

2 理论介绍

2.1 钢筋混凝土损伤理论

地震作用下结构损伤一方面是由结构的变形产生的；另一方面是由于结构在变形过程中对地震能量的消耗。结构相对能量方程为：

(1)

动能、阻尼耗能、结构变形能构成了结构的总能量，其中变形能最终也会以阻尼或滞回耗能的形式耗散，滞回耗能是结构地震损伤的重要原因。基于上述原理，Ang、Park量化了综合考虑能量和位移参数的地震损伤模型：

(2)

β=(-0.447+0.073λ+0.24n0+0.314ρt)×0.7100ρω

(3)

式中：λ为剪跨比，小于1.7时取1.7；n0为轴压比，小于0.2时取0.2；ρt为全部纵筋配筋率，小于0.75%时取0.75%；ρw为体积配箍率。

震害等级与损伤指数表量化了结构破坏程度，如表1所示。

表1 震害等级与损伤指数

2.2 结构抗震耗能能力安全系数

结构的滞回耗能能力可由式(2)得到：

(4)

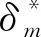
D0确定后，EH可由式(4)得到。而滞回耗能在结构总耗能的占比仅与结构本身的动力特性有关。

EH=ηHEI

(5)

式中：ηH为滞回耗能所占总耗能的比例;EI为总耗能。

滞回耗能作为结构主要的耗能，一般占总耗能的25%～70%。将结构总耗能EI定义为结构在控制条件下的有效抗震耗能能力CA,有：

(6)

地震总输入能用DM表示：

(7)

地震动总输入能的计算可以由非线性时程分析直接积分得到，也可以由结构弹性反应的总输入能计算得出。采用弹性的方法计算地震动总输入能DM时，应引入修正系数进行修正：

DM=(1+η)DM0

(8)

式中：η为修正系数，建议取值0.05；DM0为弹性方法算得的地震动总输入能。

定义结构抗震耗能能力安全系数ρ为结构的有效抗震耗能能力与抗震耗能需求的比值，可以表示为：

(9)

若ρ>1，表示结构的抗震性能满足要求；反之若ρ<1，则表示结构的抗震性能不足。评估流程见图3。

图3 评估方法基本流程图

3 不同参数模型的抗震性能分析

该文将对曲率半径及墩高两大参数对连续刚构桥抗震性能的影响进行分析，文中选取H=58 m，R=500、1 000、2 500、∞ 4个模型及R=1 500 m，H=38、78、98、118 m 4个模型。模型1为原模型，其他模型的编号具体如表2所示。

表2 不同参数模型编号

3.1 有限元分析模型的建立

结构采用Abaqus建模，混凝土采用C3D8单元，钢筋采用T3D2单元模拟，两者进行嵌入绑定。考虑结构刚度较小，对墩底直接进行固结处理，不考虑桩土效应。模型如图4所示。

图4 桥梁结构有限元模型

通过选波工具选取经调幅后的ORG-wv2波、HYUGANADA波，分析不同模型在最不利激励方向下不同地震波激励的地震响应。

3.2 有效抗震耗能能力计算

通过对结构在各地震波不同峰值加速度及不同激励方向下的弹性时程及弹塑性时程分析，得到各模型墩顶最大位移，如表4所示。

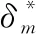
表4 各模型在不同地震波下的墩顶最大位移

续表4

模型编号峰值HYUGANADA波纵桥向/cm横桥向/cmORG-wv2波纵桥向/cm横桥向/cm80.10g17.2815.039.0211.580.15g25.9223.1013.5216.7990.10g31.5718.907.5211.410.15g47.3427.5411.1816.29

与各模型的屈服位移值比较可知：模型2、3、4在0.15gHY波纵、横桥向激励下进入屈服，模型6在0.10gHY波横桥向激励下、在0.15gHY波纵、横桥向激励下、在ORG波横桥向激励下进入屈服状态。这些状态下的结构抗震耗能能力按实际位移进行计算。

不同峰值地震波对不同墩高及不同曲率半径模型的能量输入历程对比曲线如图5、6所示(仅列出HY波0.15g峰值加速度下的对比曲线)。

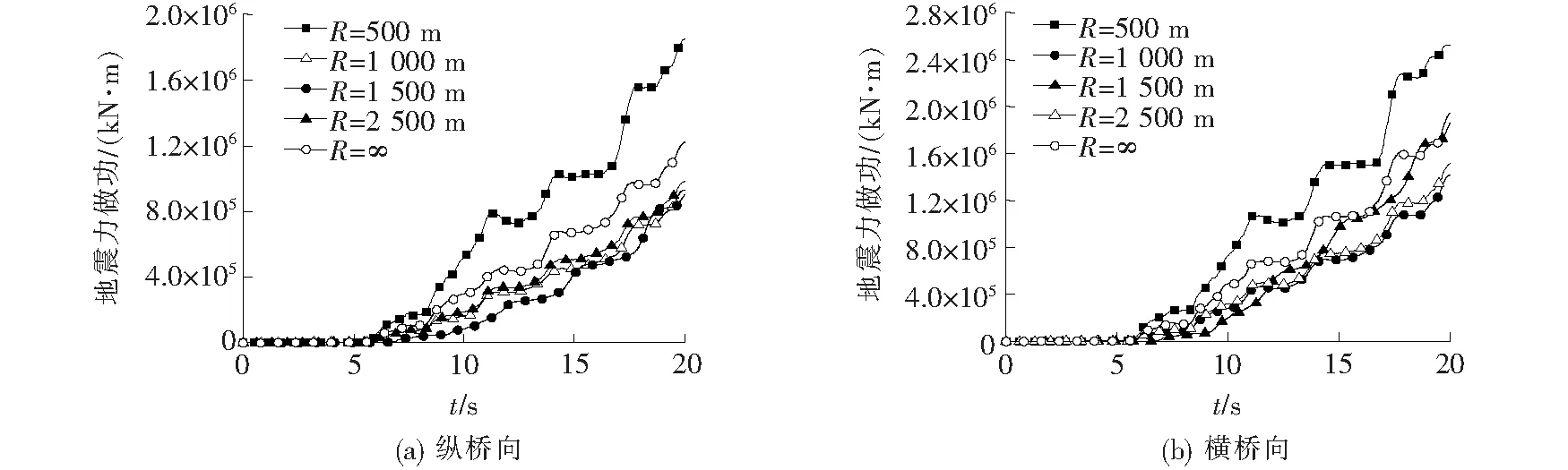
图5 0.15g峰值加速度下不同曲率半径模型外功历程对比曲线(HYUGANADA波)

图6 0.15g峰值加速度下不同墩高模型外功历程对比曲线(HYUGANADA波)

由图5、6可知：同等峰值加速度地震波对不同曲率半径与不同墩高模型的能量输入历程曲线有明显的差异。横桥向地震动总输入能大于纵桥向，曲率半径为500 m时的地震动总输入能明显大于其他半径，曲率半径为1 500 m时的地震动总输入能最小，HY波下38 m墩高模型的地震动总输入能最大，ORG波下78 m墩高模型的地震动总输入能最大。地震波特性和结构本身特性都影响着结构总输入能的大小。

该文对9个模型在0.15g下纵、横桥向的抗震耗能能力安全系数进行计算，结果如表5所示。在计算中，地震总输入能考虑1.05的修正系数。

表5 各模型抗震耗能安全系数计算结果

续表4

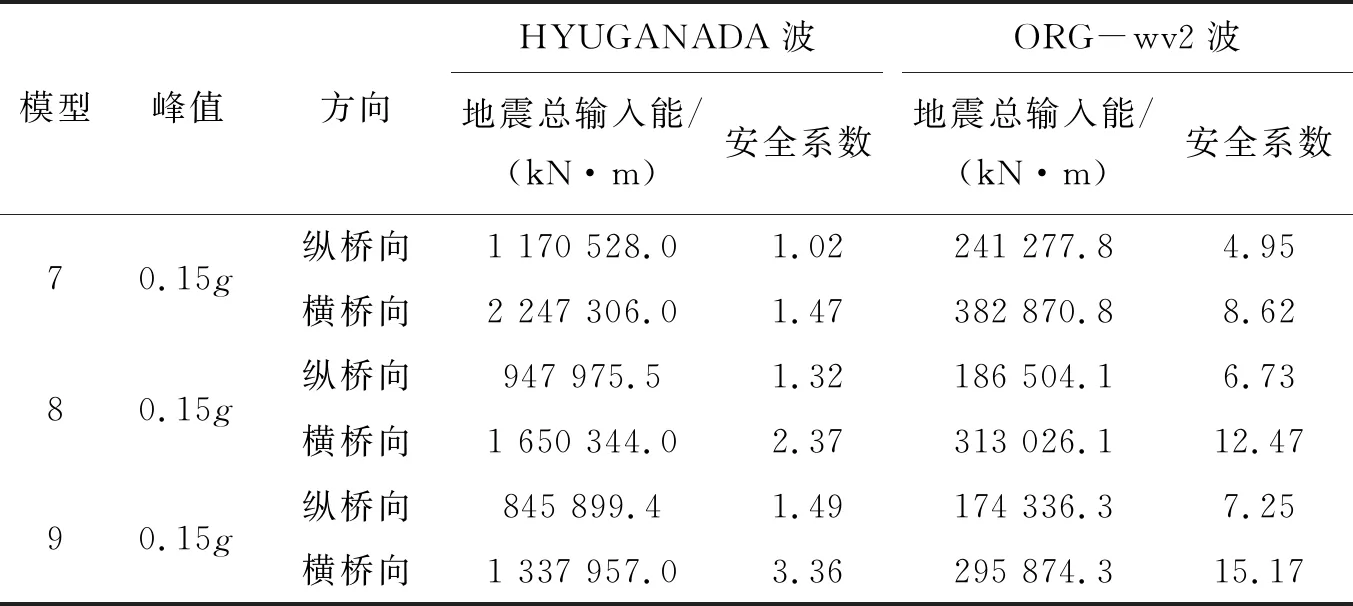
模型峰值方向HYUGANADA波地震总输入能/(kN·m)安全系数ORG-wv2波地震总输入能/(kN·m)安全系数70.15g纵桥向1 170 528.01.02241 277.84.95横桥向2 247 306.01.47382 870.88.6280.15g纵桥向947 975.51.32186 504.16.73横桥向1 650 344.02.37313 026.112.4790.15g纵桥向845 899.41.49174 336.37.25横桥向1 337 957.03.36295 874.315.17

由表5可知：抗震耗能安全系数最小出现在0.15gHY波作用下的模型6纵桥向，为0.28；0.15gHY波下模型6的纵、横桥向，0.15gHY波下模型2的纵桥向，0.15gHY波下模型5的纵桥向抗震耗能安全系数均小于1，存在较大倒塌的风险；在各峰值加速度ORG波下各模型的抗震耗能安全系数均大于1，表明结构还有较大的抗震耗能能力储备。对比不同曲率半径的模型，地震动总输入能最大出现在模型2(R=500 m)，对比不同墩高的模型，地震动总输入能最大出现在模型6(H=38 m)。

4 结论

基于能量原理与双重破坏准则，研究了曲率半径、墩高等参数对某大跨曲线连续刚构桥抗震性能的影响，得到如下结论：

(1) 总输入能的大小既与地震动特性有关，也与结构本身的特性相关，地震动特性对结构总输入能的影响较结构本身特性对其的影响大。

(2) 计算得到的结构抗震耗能能力安全系数，不仅可以判断结构是否超出了抗震耗能能力，还可定量反映出耗能能力的贮备大小，同时也规避了位移验算安全但损伤超限造成的结构倒塌风险。

(3) 高墩大跨曲线连续刚构桥抗震耗能能力随墩高的增加而增大，随曲率半径的增大而减小，横桥向的抗震耗能能力大于纵桥向；总而言之，高墩的抗震性能大于矮墩，曲线桥的抗震性能大于直线桥。