劈尖干涉的仿真与分析

周薇薇，平兆艳，刘芳芳，赵 旺

( 淮南师范学院 化学与材料工程学院, 安徽 淮南 232038)

两块平板玻璃，一端重叠，另一端相隔很小距离，这两块玻璃之间的空气薄膜就构成了空气劈尖。光线垂直入射时，在劈尖上、下表面反射的两束光满足相干条件，产生明暗相间的干涉条纹。在实际工程应用中，劈尖经常用于检查工件表面平整度、测量金属丝直径等，除此之外，还可以测量劈尖夹角[1]、激光波长[2]、液体和透明固体的折射率[3]，甚至进一步测量金属丝杨氏模量[4]、磁致伸缩系数[5]、混凝土热膨胀系数[6]等。系统研究劈尖干涉规律，对掌握光的干涉原理及其应用具有重要意义。

影响劈尖干涉的因素包括劈尖夹角、劈尖折射率、入射光波长等。除此之外，在实验过程中，玻璃表面存在的缺陷或污染物可能导致劈尖的重叠端不能保持紧密接触，也会影响到干涉条纹。利用计算机辅助的仿真技术对光的干涉现象建模，可以便捷高效的重现干涉图像并分析各种因素对干涉图像的影响[7,8]。Origin是一个在学术和工程中应用较广的软件[9,10]，科学绘图与数据分析功能强大，图形化用户界面友好，不依赖编程。本文使用Orgin软件对劈尖干涉进行实验仿真，分析了干涉条纹特征，并深入探讨了不同参数对干涉条纹的影响。

1 实验原理

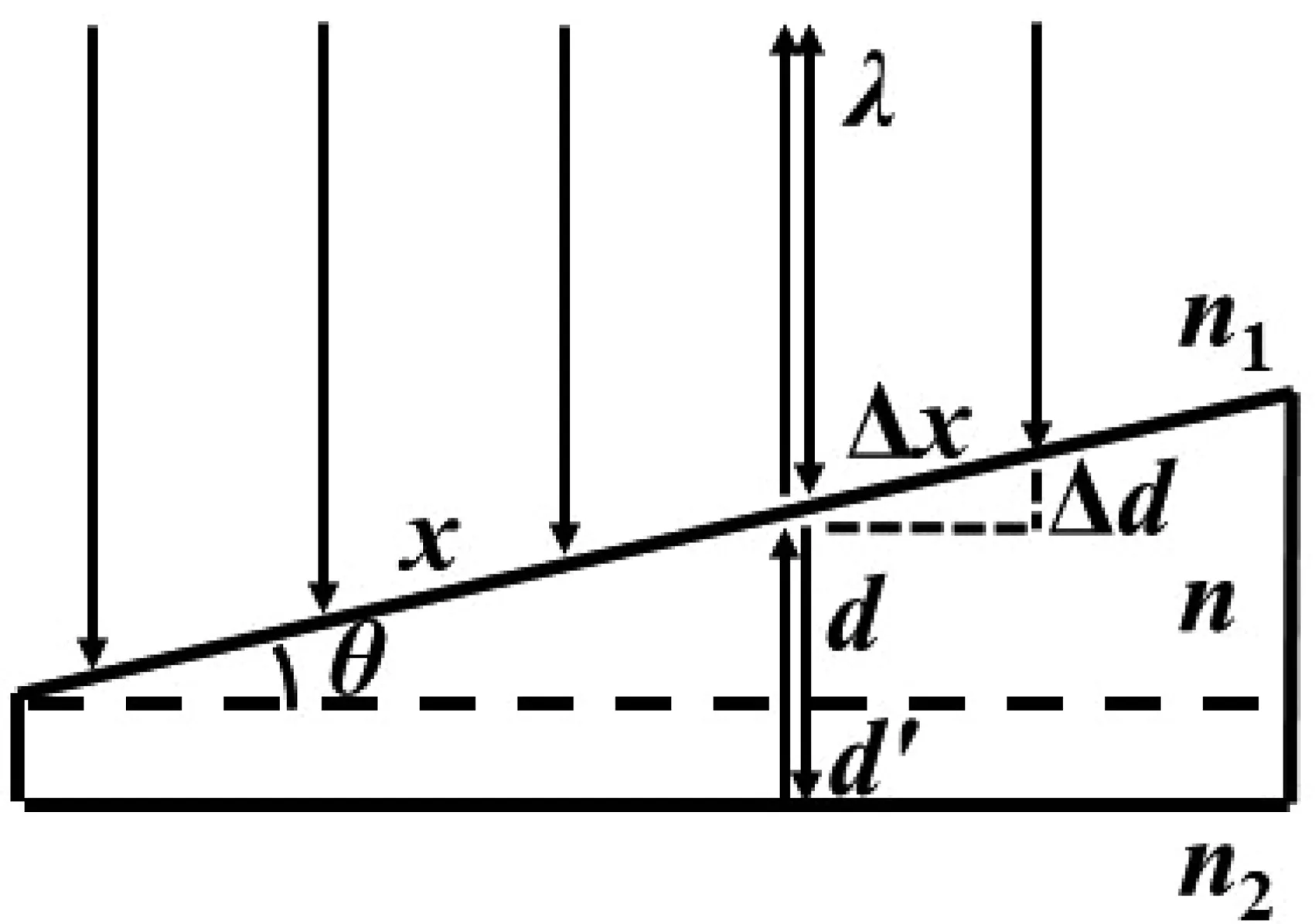
图1 劈尖干涉实验装置示意图

劈尖干涉实验装置如图1所示，设入射光波长为λ，劈尖夹角和折射率为θ和n，由于缺陷或污染物造成的劈尖上表面竖直平移位移用d′表示。考虑入射光在劈尖上、下表面反射所导致的附加光程差，劈尖厚度为d+d′处总光程差δ为：

(1)

根据光的干涉理论，产生亮纹的条件是：

δ=kλ

(2)

产生暗纹的条件是：

(3)

其中k=0，1，2，3，...代表干涉条纹的级数。

综合(1)、(2)和(3)式，可得第k级亮纹的高度为：

(4)

第k级暗纹的高度为：

(5)

由于θ值极小，接近于零，满足：

sinθ≈tgθ≈θ

(6)

根据图1中几何关系，可以得出：

d=xsinθ=xθ

(7)

假定两列相干光的光强I相等，而光强I与振幅A的平方成正比，因此A也似相等，即I1=I2=I0，A1=A2=A0，则

(8)

(9)

因此，劈尖干涉条纹的光强分布如下式：

(10)

2 实验仿真

采用Origin软件进行劈尖干涉的实验仿真，所用版本为2019学习版。启动软件后，第一步，点击File-New-Matrix新建一个矩阵，x轴表示劈尖条纹的位置，为了显示精细，设定行数为1000，取值区间为[0, 2] mm；y轴表示每条劈尖条纹的宽度，可设定行数为10，取值区间为[0, 1] mm；第二步，在点击矩阵左上角单元格完成全选矩阵的操作后，按照公式(10)，点击右键对矩阵元进行赋值：(cos((2*pi*n*(θ*x+d′))/λ+pi/2)))2；第三步，点击Plot-Image Plot，即获得仿真图像，以不同数值的n，θ，λ，d′参数带入赋值公式，即可获得一系列仿真图，可非常方便的探讨上述参数对干涉条纹的影响。

3 结果与讨论

3.1 典型劈尖干涉条纹

将θ=0.001 rad，n=1，λ=500 nm和d′ = 0带入公式对矩阵元进行赋值，得到典型劈尖干涉仿真结果。如图2所示，结合光强分布的剖面图，可以看出是一系列明暗相间的条纹，其特征为顶点是暗纹且条纹间距相等。

顶点位置d=0，根据公式(1)得出光程差δ=λ/2，满足光相干减弱条件，因此顶点是暗纹。值得注意的是，亮纹或暗纹的条纹间距Δx可表示为

(11)

因而，条纹间距Δx是常数。

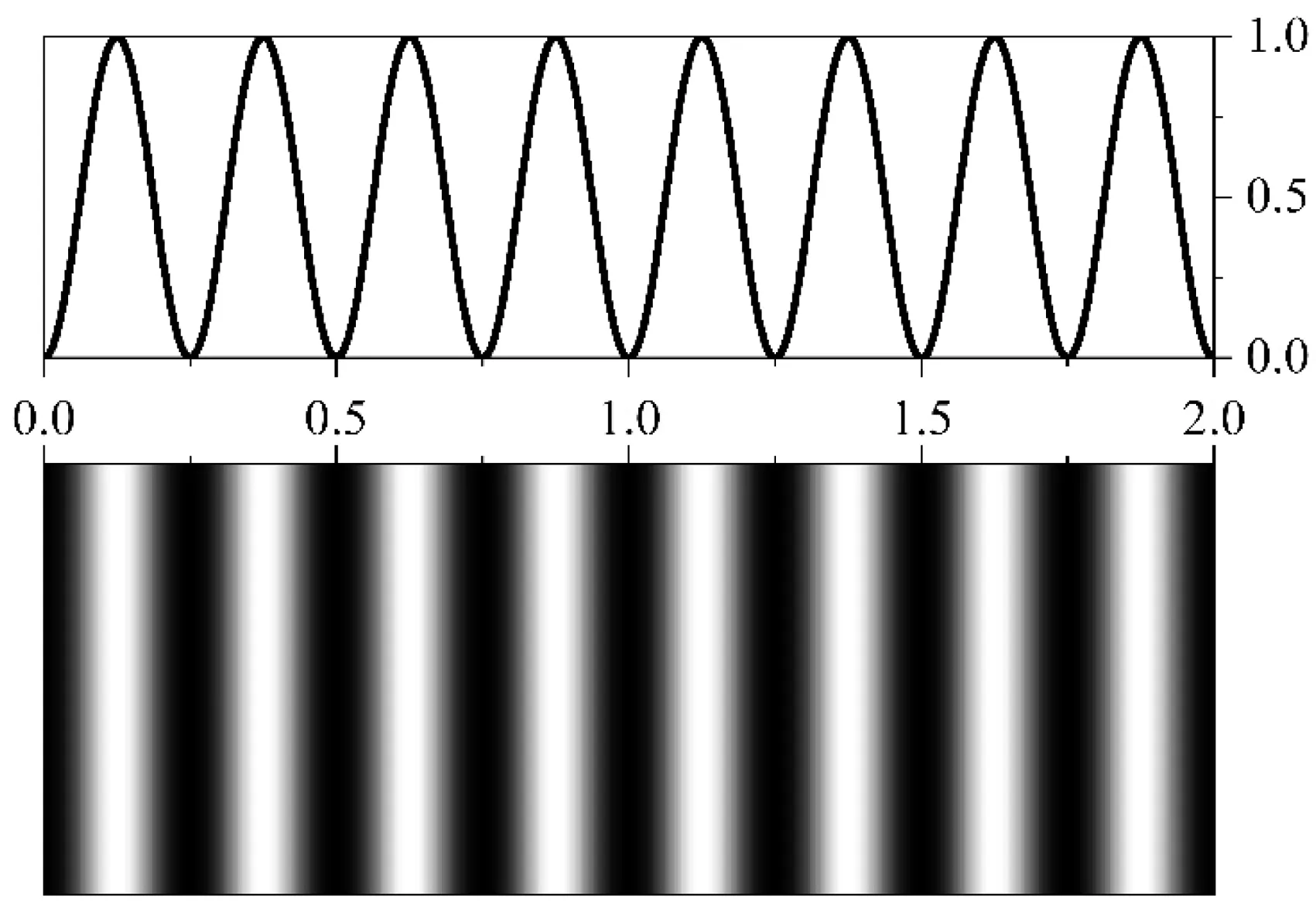
图2 典型劈尖干涉条纹及其光强分布

3.2 影响劈尖干涉条纹的因素

在其它参数不变的基础上，依次定义劈尖夹角θ值分别为0.001，0.002和0.003 rad，如图3所示得出三幅仿真图并进行对比。可以看出，在相同尺寸的空间内出现亮纹的数目分别为8，16和24条。随着θ值的增加，条纹间距随之减小。这与公式(11)中Δx∝1/θ是相吻合的。

图3 不同夹角的劈尖干涉条纹比较，从上到下依次对应θ=0.001，0.002和0.003 rad

在其它参数不变的基础上，依次定义劈尖折射率n值分别为1，1.5和2，如图4所示得出三幅仿真图并进行对比。可以看出，在相同尺寸的空间内出现亮纹的数目分别为8，12和16条。随着n值的增加，条纹间距随之减小。这与公式(11)中Δx∝1/n是相吻合的。

图4 不同折射率的劈尖干涉条纹比较，从上到下

在其它参数不变的基础上，依次定义入射波长λ值分别为500，600和700 nm，如图5所示得出三幅仿真图并进行对比。可以看出，在相同尺寸的空间内出现亮纹的数目分别为8，7和6条。不同于θ和率n，λ值的增加，导致条纹间距随之增加。这也与公式8中Δx∝λ是相吻合的。

图5 不同入射波长的劈尖干涉条纹比较，从上到下依次对应λ=400，500和600 nm

在其它参数不变的基础上，依次定义竖直平移位移d′值分别为0，500和1000 nm，如图6所示得出三幅仿真图并进行对比。可以看出，在相同尺寸的空间内出现亮纹的数目均为8条。显而易见，d′导致了干涉条纹的平移，但并不影响条纹间距，其原因就在于公式(11)中Δx与d′无关。

图6 不同竖直平移位移的劈尖干涉条纹比较，从上到下依次对应d′=0，500和1000 nm

通过以上分析可以看出，条纹间距与劈尖夹角、劈尖折射率和入射波长有关。在实验过程中，假如固定其中两个物理量，根据实验所得条纹间距就可以测定剩下的一个物理量，这就是劈尖应用的基本原理。

4 结论

劈尖干涉本质是基于分波阵面法获得相干光的等厚薄膜干涉。通过干涉光强度公式，使用 Origin软件简洁高效的复现了劈尖干涉图像，其干涉特征清晰明了；通过调整劈尖夹角、劈尖折射率、入射光波长和竖直平移位移等参数，观察其对干涉图像的影响，发现劈尖夹角和劈尖折射率增加会增加条纹宽度，入射光波长增加会减小条纹宽度，而竖直平移位移则不会对条纹宽度造成影响，但会导致条纹在水平方向的平移。