基于修正自相关算法的THz-TDS聚乙烯测厚反卷积算法

蒋 强，俞 跃，叶凌伟，郝 元

〈测量技术〉

基于修正自相关算法的THz-TDS聚乙烯测厚反卷积算法

蒋 强1,2，俞 跃3，叶凌伟1,2，郝 元4

（1. 浙江省特种设备科学研究院，浙江 杭州 310018；2. 浙江省特种设备安全检测技术研究重点实验室，浙江 杭州 3100183；3. 中国特种设备检测研究院，北京 100029；4. 中国计量大学，浙江 杭州 310018）

在聚乙烯材料管道生产制造过程中，管道厚度精确测量是影响管道生产质量的一个重要技术问题，太赫兹非金属厚度透射测量过程中，通过测量两次透射信号的光程时间差与材料折射率计算得到样品厚度参数，为了准确提取两次透射信号的光程时间差值，需要对原始时域信号进行信号表征。通过高斯滤波反卷积得到脉冲响应函数表征时域信号已经成为了一种成熟且有效的技术手段。但一方面由于太赫兹波在聚乙烯材料中的传播存在明显的频散现象，同时其透射率高回波信号较弱，导致信噪比较低，在脉冲响应函数提取过程中放大了干扰信号的比重，造成信号失真、淹没，无法准确提取信号。本文通过对带通滤波后的时域信号采用修正型自相关算法进行自相关性分析，再结合高斯滤波反卷积运算，得到改进后的脉冲响应函数。旨在解决太赫兹非金属测量领域时域信号表征问题。改进算法实验结果显示加强了信号的清晰度，解决了因杂波信号干扰造成的脉冲响应信号失真或淹没情况，显著提高了脉冲响应信号信噪比。

太赫兹；反卷积；信号表征；自相关函数；信噪比

0 引言

近年来由于天然气的广泛使用，管道作为天然气最重要的运输载体，被大量运用，聚乙烯管道因制造与安装成本低、耐腐蚀性强等优良特性更是成为首选[1]。天然气因其易燃易爆等特点极易产生安全隐患，因此对天然气管道的质量控制就显得尤为重要。特别是管道的厚度参数控制，是行业内一个难点。现有的厚度检测手段主要为超声波厚度检测，而超声波[2]由于聚乙烯材料随环境（温、湿度）变化性质改变较大，导致超声波在聚乙烯材料中传播速度不同等原因，造成测量结果误差较大，难以保证精确度，更无法作为质量合格的检验标准。由于太赫兹波对非金属材料可穿透性较强，因此被大量应用于非金属材料厚度参数求取，为聚乙烯管道厚度检测提供有力的补充。

Lionel Duvillaret利用透射样品与样品中反射的回波折射率差值求取厚度参数[3]。王秀敏提出一种误差理论分析方法测定样品厚度，确定厚度范围再选用厚度参考值，计算所有频率中的折射率，再重新选用厚度参考值重复以上工作，直到所有厚度计算完成，得出对厚度的误差曲线，选用误差最小的点，即为样品厚度[4]。李丽娟使用太赫兹单点厚度提取模型，根据太赫兹传播理论建立模型提出算法，测量出样品的厚度，但仅针对胶层厚度进行实验分析[5]。陆庆华通过对比，提出利用太赫兹光谱成像原理针对药物的厚度进行检测[6]。寇宽在Lionel Duvillaret的基础上，通过分析太赫兹波在样品不同频率中的频谱特性，分析出有效频段与无效频段，并且排除无效频段来进行厚度测量，提高了测量精度[7]。刘子烨提出使用太赫兹光子混频连续波透射成像的方法，利用其相位信息实现对样品厚度的测量[8]。

目前太赫兹非金属材料厚度求取研究中多以厚度改进算法为研究方向，测试材料也多以反射率较高的样品为主，对于反射率较低的材料并不能准确地通过两次透射样品的时域信号峰值计算得到光程时间差值，无法为厚度计算提供准确光程时间差值参数。因此，太赫兹信号信噪比低已经成为工程应用中一个亟需解决的难题。

反卷积技术作为一种成熟有效的信号表征方法被国内外学者广泛应用于信号处理问题。Zeiler[9-10]首先提出了反卷积（Deconvolution）的概念。蔡川等[11]通过反卷积技术对聚乙烯/纳米银复合材料空间电荷测量信号的恢复发现，高斯滤波器可以有效抑制恢复信号的震荡，提高测量空间电荷的分辨率。吴超一等[12]采用反卷积算法对通过脉冲电声法测量固体电介质中空间电荷测量波形进行了恢复，建立了波形衰减模型。Tanaka等[13]使用反卷积技术首次在界面电荷波形的恢复方面取得了成功。刘明亮等[14]简介了用卷积运算实现反卷积的原理、方法和实例；其次，提出了该方法的病态问题，并给出了解决的办法。邱程[15]等为实现超宽带时域测量系统的超分辨测量，将反卷积算法应用在测量系统数据处理过程中。根据测量系统中输入脉冲及输出信号的特点，选取高斯滤波器对反卷积处理带来的病态问题进行了修正，但是系统信噪比较低。Parruck等[16]发现在反卷积工程中因为一些区域中的反卷积运算误差会使得()在计算过程中被放大，造成结果存在一系列类似函数的尖刺。这些尖刺幅值很大，在反Fast Fourier transform（FFT）变换后很可能成为时域信号的主要成分，从而掩盖真实的输入信号，造成频域反卷积失败。扈罗全等[17]使用基于Tikhonov正则化方法的反卷积算法得到了真实的空间电荷分布，利用数值实验研究了噪声对反卷积算法的影响，结果表明，在无噪或者低噪环境下，反卷积算法能够非常好地计算出电介质中的空间电荷分布；在处理有噪数据时，反卷积的结果受到明显的影响，但仍然有较高的计算精度。姚若河等[18]提出了时域卷积反演算法，不仅避免了传统的傅里叶变换法所存在的缺点，且对于实际问题中由于输入和输出的起始元测量值往往幅度很小而信噪比也很小的情况，该算法能给出理想的结果。

自相关函数作为一种简单有效的信号提取方法也被大量应用于信号处理。1953年贝尔实验室利用磁带记录仪最早实现了的相关检测系统。高晋占等[19]描述了利用自相关从随机噪声中提取周期信号的方法。许峰等[20]提出一种基于相关检测的电能质量信号定位方法，能有效定位电能质量信号发生的起止时间。胡大红等[21]利用自相关函数识别时间序列变量的性质和形态，检验时间序列过程是否为零均值过程及其所建模型的适应性。刘正平等[22]提出将自相关检测与混沌理论相结合，检测微弱周期脉冲信号的检测方法。仿真结果表明在相同系统实验背景下，相结合的检测方案优于不加自相关的检测方法。吕文秋等[23]从理论上证明了多重自相关处理后信号的信噪比，比相同取样序列情况下相关处理的信噪比有所提高，比单次自相关具有更高的检测能力，同时在获得相同输出信噪比时，重自相关检测可以减小系统的复杂程度和运算时间。范晓志等[24]提出，噪声在自相关运算中的变化是随机的，因此，可以通过多次测量取平均值来消除。自相关算法有很多可以改进的地方，这主要视方法所应用的环境，若环境噪声较强且复杂，则运用多重自相关和求平均的方法可以明显改善算法的效果，对于一般噪声环境可直接利用自相关法自身的去噪能力。

天然气管道因考虑安全因素，厚度参数较大，在太赫兹厚度测量过程中因太赫兹技术的局限，使得太赫兹检测系统信噪比较低，回波接收信号弱，造成主观选取回波时间差值的误差增大，为厚度精确求取增加了难点。因此表征样本时域信号，提高回波信号信噪比显得尤为重要。本文使用了自相关函数对高斯滤波反卷积算法进行改进，以适应太赫兹非金属材料厚度测量过程中，时域信号信噪比较低造成的反卷积结果不理想等问题。同时对自相关函数进行修正，以适应太赫兹时域信号的特性。

1 实验原理

本文使用基于脉冲的太赫兹时域光谱技术对样品（聚乙烯P100标准管道试快样品）采用透射式检测方法测量以获取实验数据。如图1所示，太赫兹波发射源产生太赫兹波，首先经过首次透射在太赫兹波接收器接收到第一个脉冲信号，称为主波信号。在太赫兹波首次透射经过样品的同时在样品底面发生反射，太赫兹波在样品底面与样品表面经过两次反射后经过第二次透射在太赫兹波接收端接收到第二次透射信号，称为一次回波信号。在无样品放入的情况下即测得唯一的主波信号，称为空气参考信号。通过准确测量主脉冲信号与一次回波信号时间差值就可以精确的计算出样品厚度。

由单点测厚模型可知：

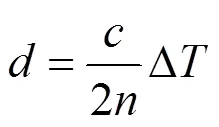
式中：d为样品厚度；n为材料的折射率；c为光在空气中的传播速度；DT为样品主脉冲与一次回波信号的时间差值。

2 算法改进原理

2.1 测量信噪比

如公式(2)所示，以一次回波信号开始与结束为两个节点，分别向两个节点左右扩展100个脉冲时间点，共200个杂波信号求取均值，以一次回波峰峰值与杂波均值比值的最大值作为信噪比以及滤波效果最优化的判别依据：

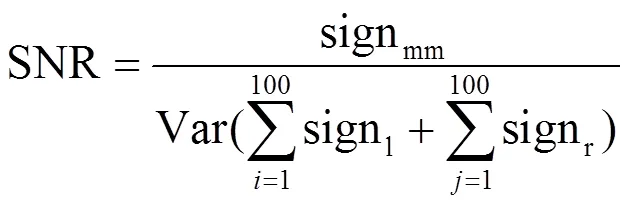
式中：SNR表示信噪比；signmm表示信号峰峰值；signl表示回波信号从信号峰峰值所在点向左取值；signr表示回波信号从信号峰峰值所在点向右取值；var表示取平均。

2.2 基于盲目反卷积的厚度测量

太赫兹时域测量系统可以简化为如图2所示的信号模型。

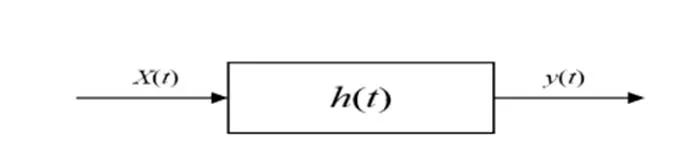
图2 系统输入输出与脉冲响应的关系

如图2所示，设()为系统的冲击响应函数，则有：

()＝()*() (3)

式中：()、()分别为系统时域输入输出信号。

()＝()() (4)

式中：()、()、()分别为()、()、()频域变换；表示有效频率。

()＝IFFT[()/()] (5)

式中：()、()分别为()、()频域变换，()为系统的冲击响应函数，表示有效频率。

由于系统属于盲目反卷积系统，所以需要对输入信号进行假设。太赫兹时域系统是以皮秒激光器为辐射源信号，因此可以忽略信号在空气中的损失。本文通过以空气参考时域信号模拟系统输入信号得到输入信号()。由图2可知，当输入信号的()信噪比较低时，()在有效信号区域的信号强度会因为聚乙烯材料对辐射的吸收与反射等造成信号回波较弱，电场强度很小甚至为零，通过运算得到的()就会很小，使信号淹没在杂波信号中无法识别。要利用反卷积算法来提高系统的分辨率，首先必须解决信号的信噪比较低带来的信号损失问题。

2.3 基于带通滤波的信噪比改进方法

由式(5)可知，当输入信号的()带宽有限，()在一个或多个频率区域的幅值很小甚至为零，通过运算得到的()就会突然增大，成为一系列的尖刺。这些尖刺幅值很大，在逆傅里叶变换后很可能成为时域信号的主要成分，从而掩盖真实的输入信号，造成频域反卷积失效。同样如果在某些频点上，输入和输出信号都很小甚至为零，那么得到的结果就完全是一个不确定的噪声信号。这也就是反卷积运算普遍存在的病态性的问题。

要利用反卷积算法来提高系统的分辨率，其次必须解决反卷积算法带来的病态问题。

太赫兹时域测量系统的传递函数主要呈现低通特性，为了消除()的尖刺，需要设计一种低通滤波器()来对其进行处理，从而得到稳定、平滑的估值。由于测量系统杂波信号为高斯白噪声信号，而且高斯信号在频谱上表现和低通滤波器类似，所以在反卷积过程中采用合适的高斯滤波器可以有效地保留冲激响应信号同时去除高频的尖刺。

反卷积算法高斯滤波器滤波处理能够有效剔除显著杂波干扰信号，这使得信号变得平滑。但无法解决信号比较低带来的信号损失问题，无法提高信号信噪比。在太赫兹聚乙烯材料厚度测量过程中，由于硬件系统信噪比有效区间的限制，在太赫兹波区间内（0.1THz～10THz）存在大量信噪比较低频段所带来的杂波干扰信号，这使得信号本身带有大量的无效频段太赫兹信号，为了滤除无效的信号频率区间，需要对信号进行预处理操作。

运用巴特沃斯滤波器带通特性对信号步进式带通滤波，先确定带通滤波器上下限，采取稳定一边，另一边0.01THz的步进值进行信噪比计算，直到操作边出现信噪比转折点即确定滤波上截止频率（下截止频率），重复操作另一边，即可得出相对最优化滤波区间。滤除无效频率区间，得到较理想的时域信号。结果显示巴特沃斯滤波器能够有效滤除无效频段太赫兹信号，显著提高信号信噪比：

(＋0)＝(＋0)(＋0) (6)

式中：0表示无效频率。

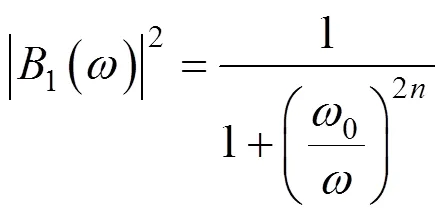
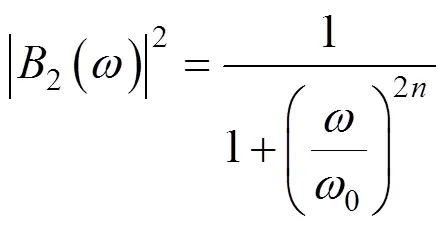
¢(＋0)＝(＋0)()＝()×＋(0)×(9)

式中：代表带通滤波器；、表示权值。

2.4 修正自相关算法

自相关算法是一种衡量单一信号时域序列在不同时间点的相关程度的工具。通过与移位之后的自身信号遍历相乘即可得出各个时域信号之间的相关系数。可以更加清晰提取隐藏或淹没在杂波信号中的有效信号，提高信号信噪比。根据相关系数定义可以得出自相关函数在时间序列中的表达式：

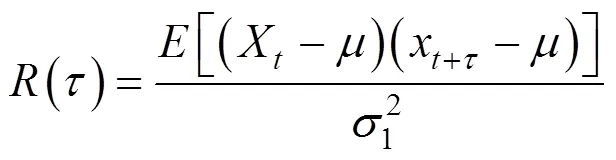
式中：()为自相关系数；12为时间序列方差；为序列均值。

假设信号的复信号形式为：

()＝ej(2p＋)＋()＝1,2,3… (11)

式中：为信号频率；、分别为幅度和初相；()为高斯白噪声序列，其均值为0，方差为22。对()进行自相关运算，得：

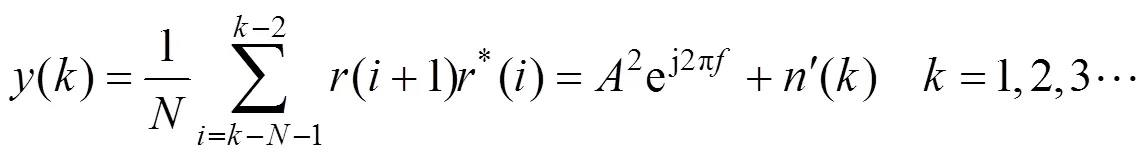
式中：为序列长度；*()为对输入信号共轭；¢()为含有噪声项的自相关运算结果，其表达式为：

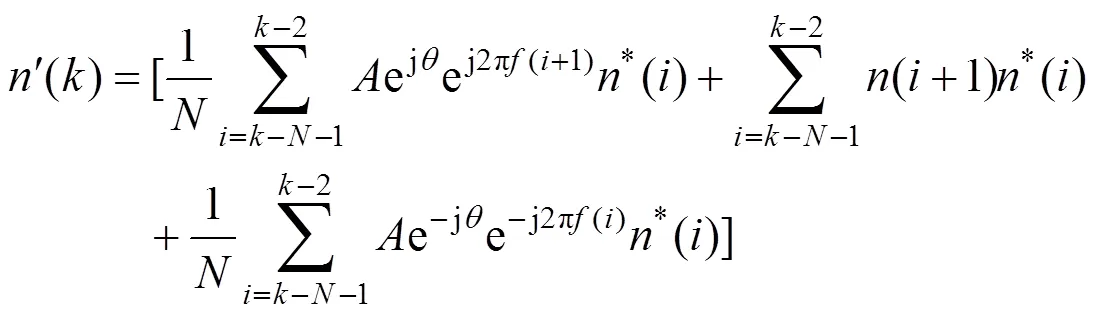
当较大时，根据概率论中的中心极限定理，¢()可以看作近似高斯分布，其均值为0，方差等于(222s22＋s24)/因此，()的信噪比为：

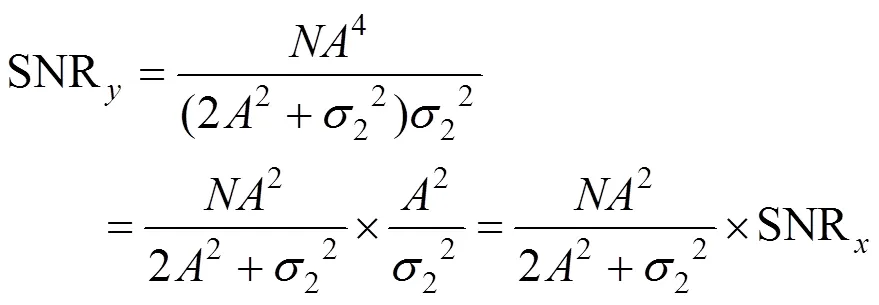
从式(14)可以看出，相比于原信号，信噪比提高了/(2＋22/2)倍，相关输出()的信噪比与序列长度成正比与2/成反比。2/越小代表杂波信号越平稳，则复合信号越平稳。

算法1为伪代码实现，其中第1行包括各类常量定义、变量定义与赋初值操作，第2～28行遍历各个待布局逻辑功能，将各项约束写入模型，第29行定义目标函数，最后调用求解器对模型进行求优.由表1可知，P=2为常数，同时对于目前FPGA芯片规模来说F，W，H通常也很小[8]，因此建立布局模型的时间复杂度为O(N2).由于MILP求优的时间复杂度为指数阶，因而UPRFloor模型的求优时间复杂度和文献[10]均为O(2N).

自相关函数的使用前提是平稳序列，即在统计学自相关函数中要求期望值为0，方差为1，且方差和期望不随时间的变化而变化，而太赫兹时域信号序列不能等同于平稳信号序列，所以应用传统自相关函数计算自相关系数时并不能准确表征原始信号。由式(15)可知，在自相关算方法中，由于补零操作移位之后的时间序列的均值会逐渐缩小并趋近于0，也随着减小并趋近于零。时间序列在不断的补零操作下会成为绝对意义上的零均值序列，因此只有时变的序列均值可以反映序列真实方差的变化。只有时变的方差才能反映移位后离散序列的离散程度。因此，结合太赫兹时域信号随时间变量改变对应期望与方差也随之改变的特点，进而采用修正自相关公式进行处理：

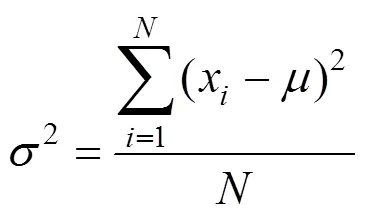
修正自相关公式如下：

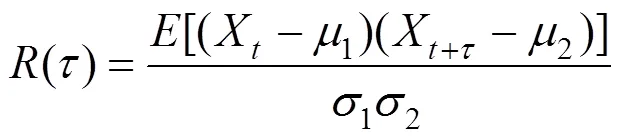
式中：()为修正自相关系数；1、2分别为原序列与延时后时间序列标准差；1、2分别为原序列与延时后时间序列均值。

对比公式(10)(16)，可以发现自相关算法（公式(10)）使用了同一个均值与方差对移位前后的时域信号序列进行处理，修正自相关的算法（公式(16)）使用各自的均值与方差对公式进行表达。随着自相关序列的延迟时间增加，脉冲函数的的主信号会被后面的递补杂波信号取代为信号序列，由于杂波信号的均值为0，时移序列的均值也会相应减小，因此当序列长度N已经选定时，信号的信噪比也会相应提高。

综上，本文改进反卷积算法如图3所示。

1）通过实验获取非金属太赫兹时域光谱系统测量时间序列，以空气参考信号为基准对空气参考信号和样本信号进行归一化处理；

2）以空气参考时域信号模拟系统输入信号得到输入信号()，太赫兹时域光谱系统测得样本时域输出信号()。

3）通过经典滤波器（巴特沃斯滤波器）对样本信号进行滤波预处理，得到最优化滤波样本时域信号。

4）分别对空气参考信号与最优化后的时域信号进行自相关性分析；得到各自的自相关系数时间序列。

5）通过对空气参考自相关系数时间序列和样本信号自相关系数时间序列进行高斯滤波反卷积运算，提取出信号的脉冲响应函数。

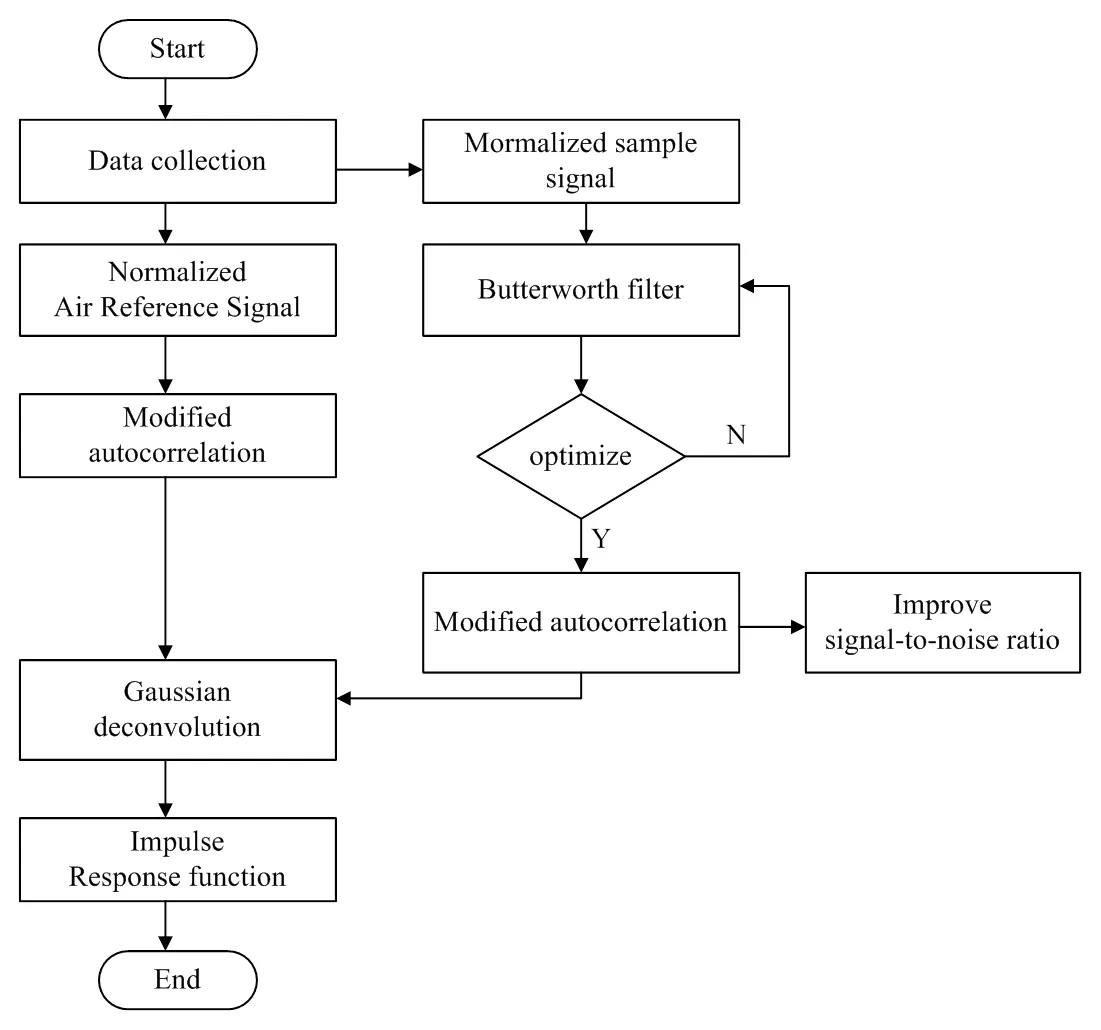
图3 反卷积算法改进流程图

3 实验与结果分析

3.1 实验装置

如图4所示，实验采用太赫兹时域光谱（THz-TDS）系统，飞秒激光设备参数为：波长800nm、脉宽100fs、频率80MHz。系统原理为钛宝石飞秒激光器经过分束镜将飞秒激光分为泵浦光、探测光。泵浦光通过可变延迟线入射到光导天线晶体上激发出太赫兹脉冲；探测光经过多次反射后与太赫兹脉冲一同通过探测晶体，用于探测出太赫兹脉冲的电场强度随时间变化情况。实验环境温度为25℃（室温），环境湿度为30%。

3.2 算法改进实验

本文实验数据来源于聚乙烯P100样品测试结果，其中时域信号取1200组数据，自相关系数图取半图谱，即向右平移1024个单位，脉冲响应函数与自相关系数图对应取1024组。时域图横坐标为归一化时间，单位为0.1ps，纵坐标为归一化电场强度，单位为V，自相关系数图横坐标为归一化时间，单位为0.1ps，纵坐标为自相关系数，单位为常数，脉冲响应函数图横坐标为归一化时间，单位为0.1ps，纵坐标归一化电场强度，单位为V。为了统一化图示，便于观测，横坐标统一标示为time/ps－1，纵坐标统一标示为power。

已知A为8mm厚度聚乙烯样品，图5(a)、(b)分别为样品滤波信噪比值分布图、滤波器频域响应图。结合表1所示通过滤波频段选取方法得出A样品的最佳滤波区间为0.84～1.09THz，其中基准滤波信噪比值为138.5674。0.84THz频率处的滤波信噪比值144.5，1.09THz频率处的滤波信噪比值达到最大为533.2。

图6所示为空气参考信号与样本信号的时域图，图中所示实线为样本信号，虚线为空气参考信号，标注点为样本一次回波信号所在。由表1所示可得样本原始信号回波峰峰值信噪比为4.7525，信噪比较低。不易从图中直接获得样本信号主回波时间差值。由于采用透射式测量方法，主波峰值滞后142ps，其中参考信号峰值在125ps处，样品时域信号主波峰值位于267ps处，样品回波信号峰值点滞后主波峰值点80.2ps，位于1070ps处。

图7所示为巴特沃斯滤波处理后的样品时域信号，图中标注为样本一次回波峰值点，由表2所示可得样本巴特沃斯滤波后信号回波峰峰值信噪比为15.2329，是原始信号回波信噪比的3.21倍。由此可以说明巴特沃斯滤波器对回波信号具有显著提高信号信噪比的作用。

图8、9、10所示分别为参考信号、样本信号自相关系数图、样本信号巴特沃斯滤波处理后自相关系数图，如图9所示自相关系数在80.2ps处最大，与图1中样本时域信号主回波峰值时间差值相吻合，即在右移802ps个时间单位后，出现回波自相关系数峰值点。由表2所示可得样本自相关系数信噪比为5.9462，是原始信号回波信噪比的1.25倍。信噪比提高不明显，说明自相关系数无法明显提高信号信噪比。由图10与表2所示可得样本巴特沃斯滤波后自相关系数信噪比为28.7159，是原始信号回波信噪比的6.04倍。信噪比提高明显，再次说明巴特沃斯滤波器对信噪比提高效果显著，同时也说明自相关系数在表征时域信号时存在大量杂波干扰，无法准确反映信号特征。

图11、12、13所示分别为空气参考信号巴特沃斯滤波处理后修正自相关系数图、样本修正自相关系数图、样本信号巴特沃斯滤波处理后修正自相关系数图，由图10与图11、图12与表2中4、5、6所示可得样本修正自相关系数信噪比为26.7989，样本信号巴特沃斯滤波后自相关系数信噪比为28.7159，样本巴特沃斯滤波后修正自相关系数信噪比为30.8711，考虑到过程中的误差，三者信噪比基本一致，可以得出自相关系数在相对最优化滤波之后的效果等同于修正自相关系数，而后者更能体现原始信号的特征。

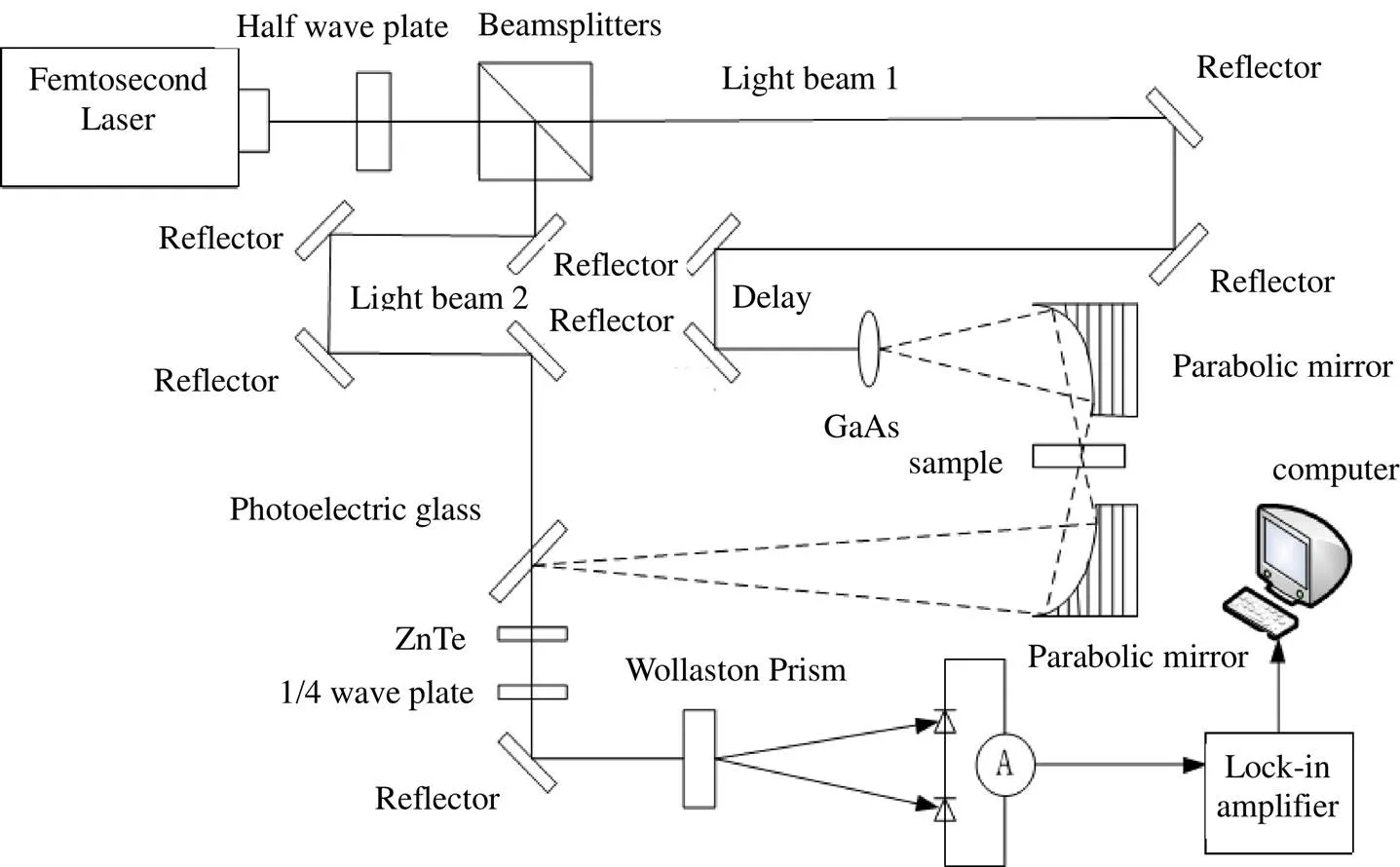
图4 太赫兹时域光谱检测系统

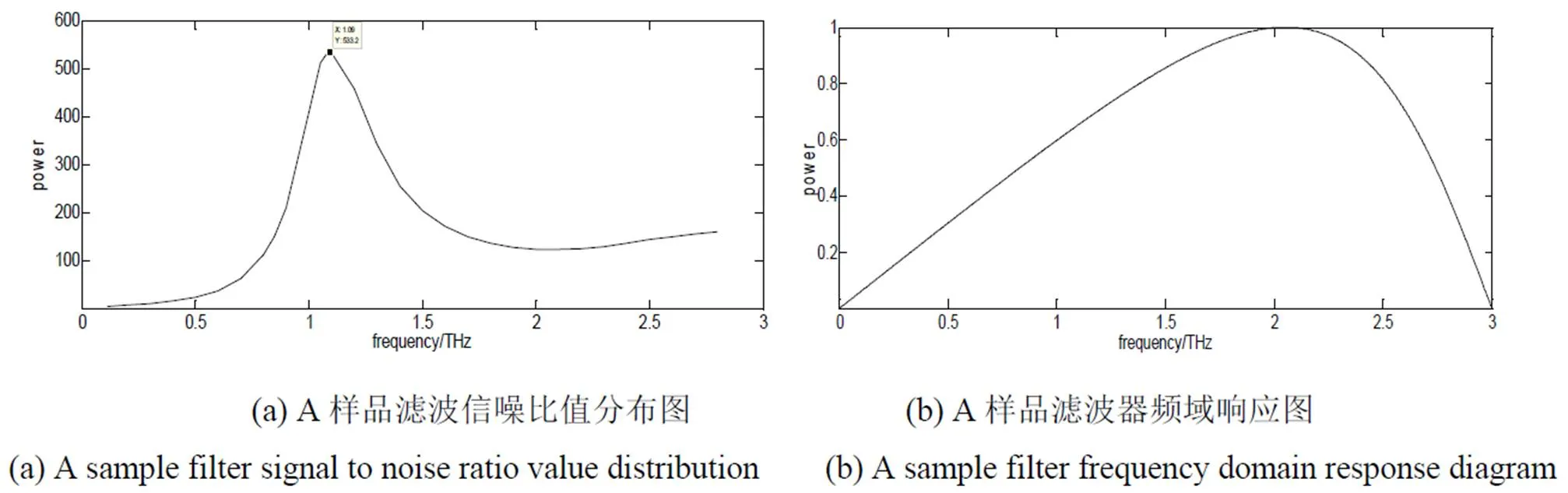
图5 有效频段滤波

表1 信噪比比对结果

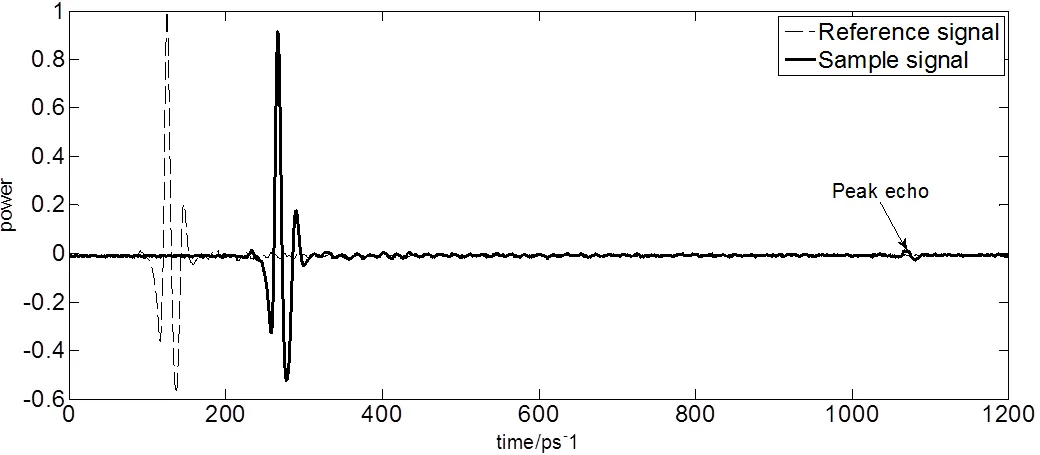
图6 空气参考信号与样本信号时域信号

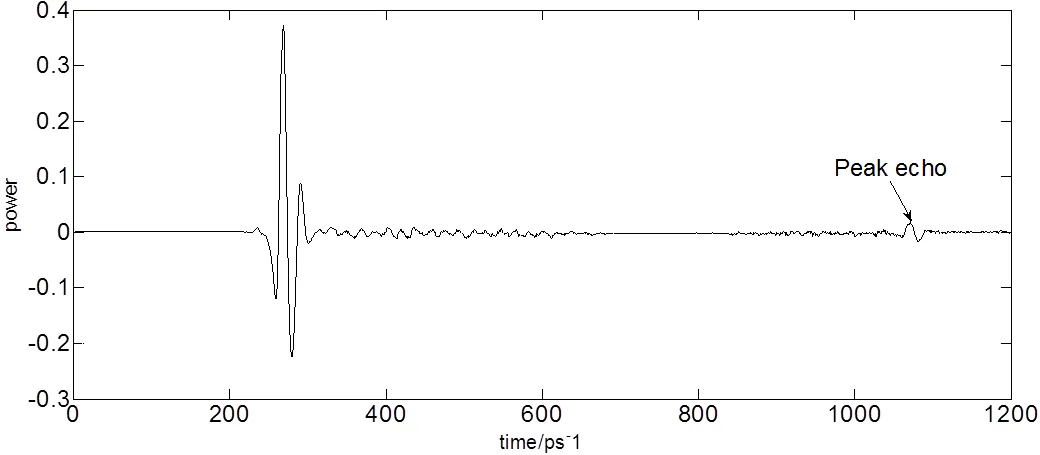
图7 巴特沃斯滤波处理后的样品时域信号

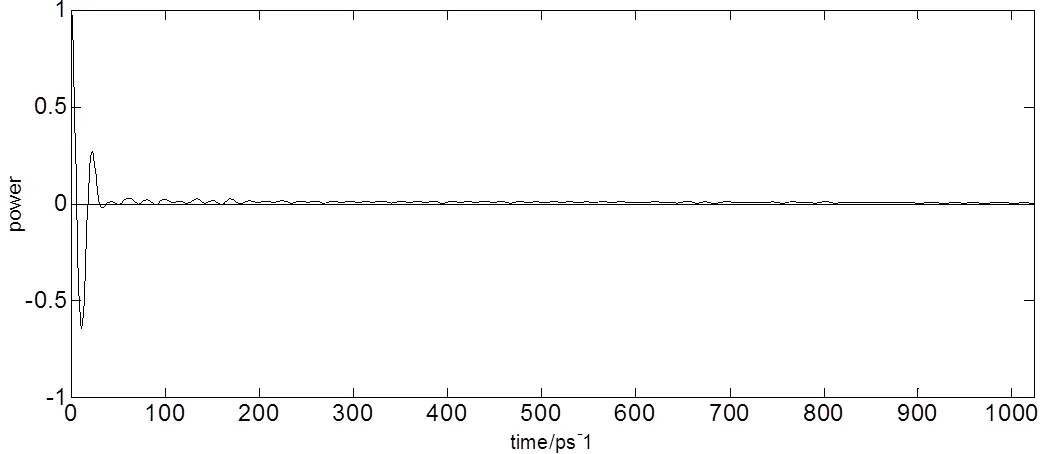
图8 空气参考信号自相关系数图

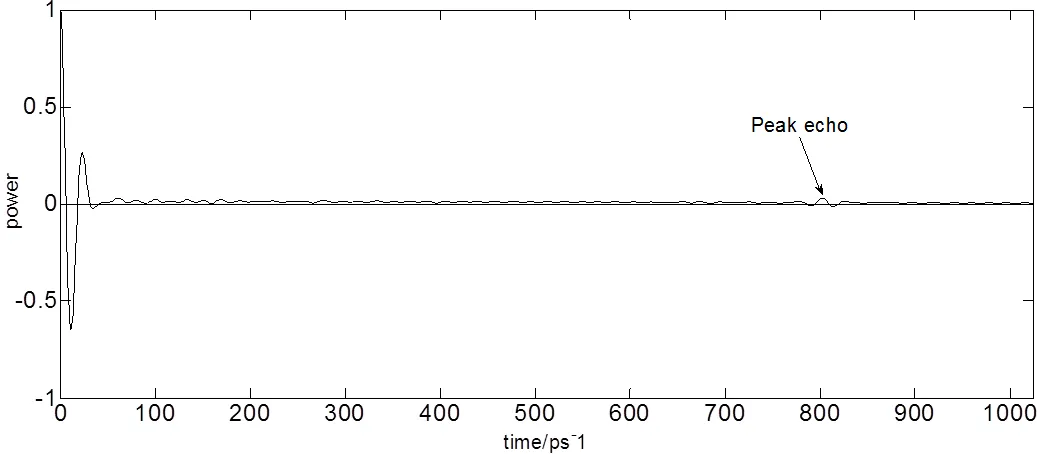
图9 样本信号自相关系数图

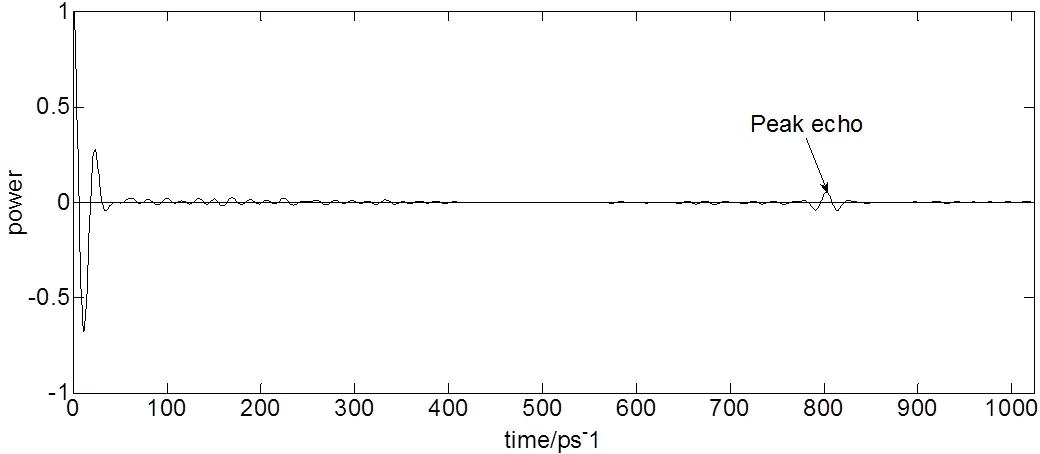
图10 样本信号巴特沃斯滤波处理后自相关系数图

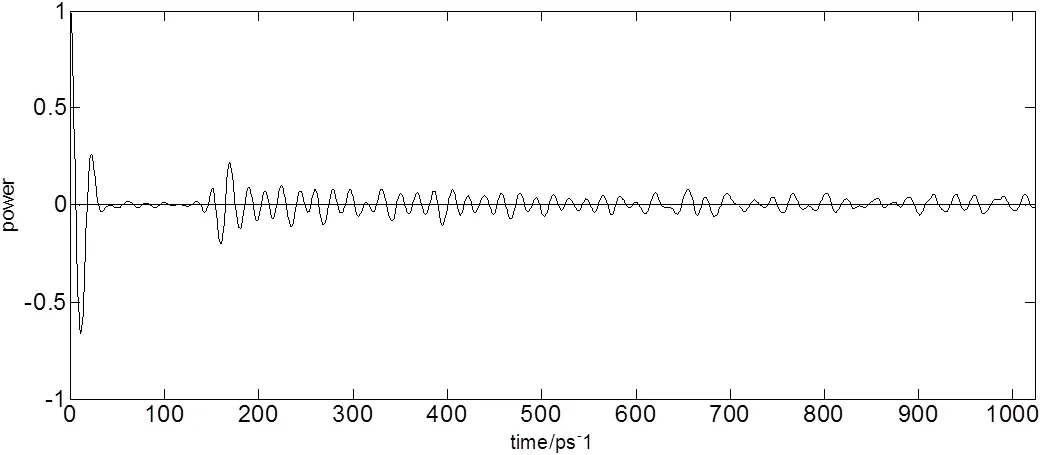
图11 空气参考信号巴特沃斯滤波处理后修正自相关系数图

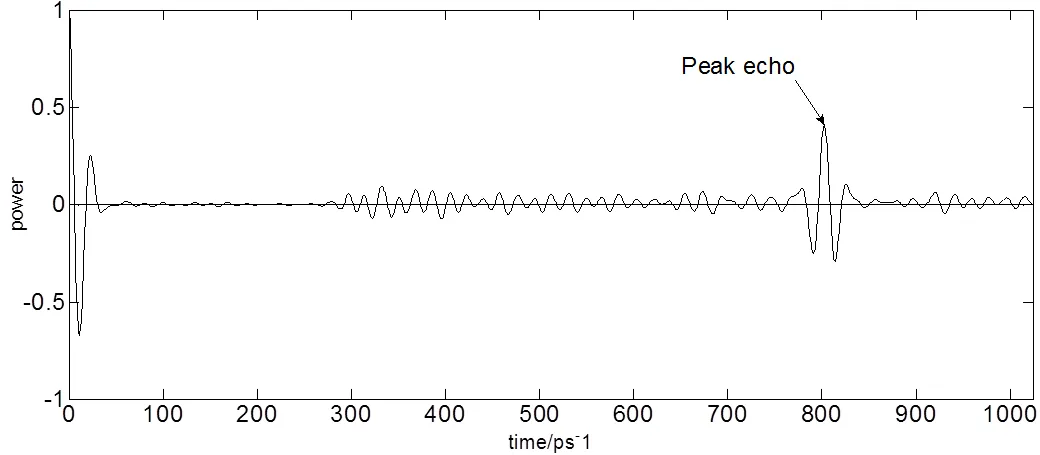
图12 样本信号修正自相关系数图

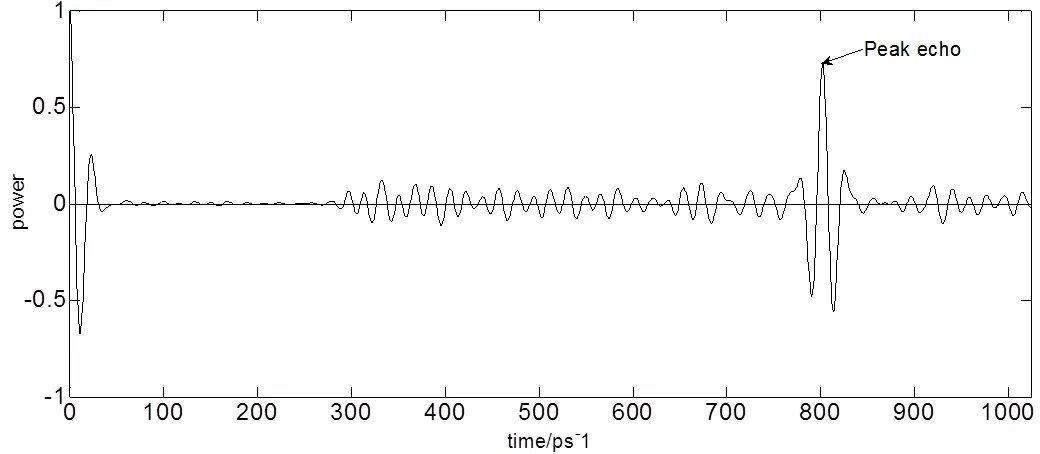
图13 样本信号巴特沃斯滤波处理后修正自相关系数图

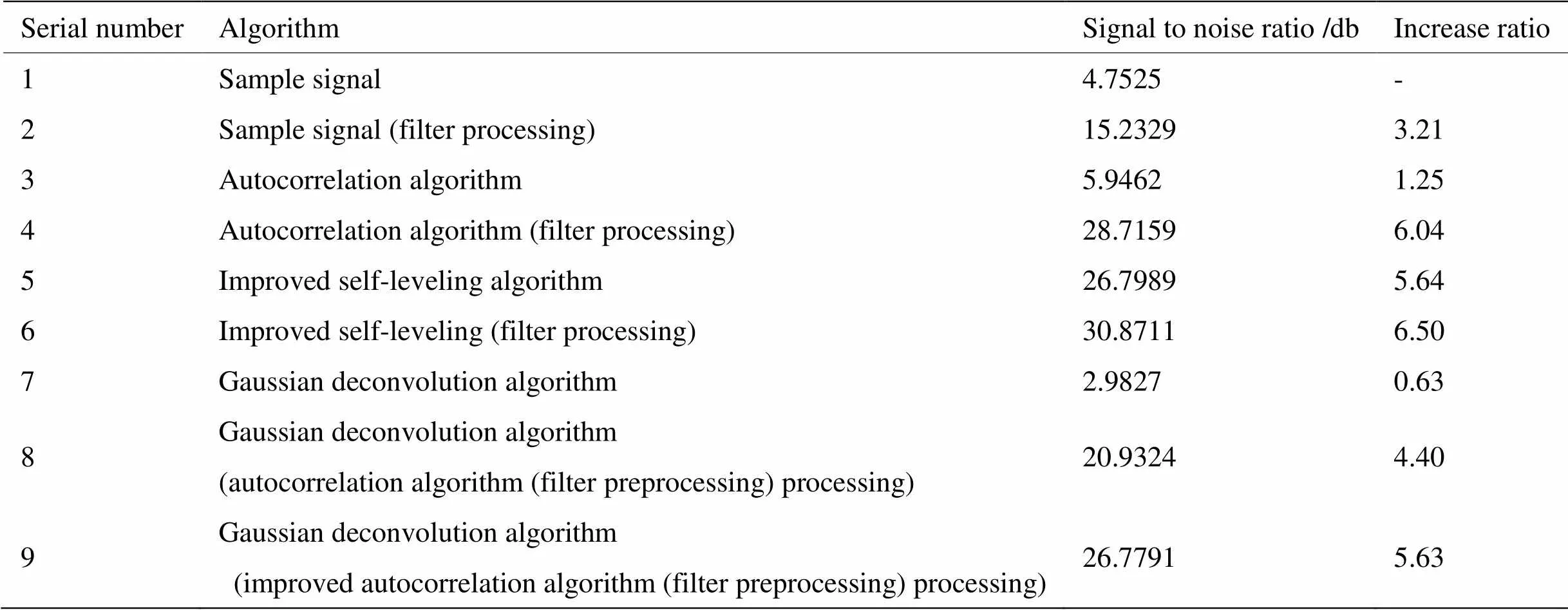
表2 信噪比比对结果

图14、15、16所示分别为脉冲响应函数（未处理）、脉冲响应函数（滤波后自相关算法处理）、脉冲响应函数（滤波后修正自相关算法处理）。表2中7、8、9所示依次对应3种方法的处理结果。信噪比分别为2.9827、20.9324、26.7791。分别为原始信号信噪比的0.63倍、4.40倍、5.63倍。由结果所示，直接通过高斯滤波反卷积算法得到的脉冲响应函数的结果显示杂波干扰无法有效去除，无法直接适用于太赫兹非金属反射式测量方式，经有效滤波后自相关算法处理后的脉冲响应函数与经有效滤波后修正自相关算法处理后的脉冲响应函数均能达到提高信噪比、表征时域信号的目的，但后者效果更加突出，更能体现时域信号的特征。

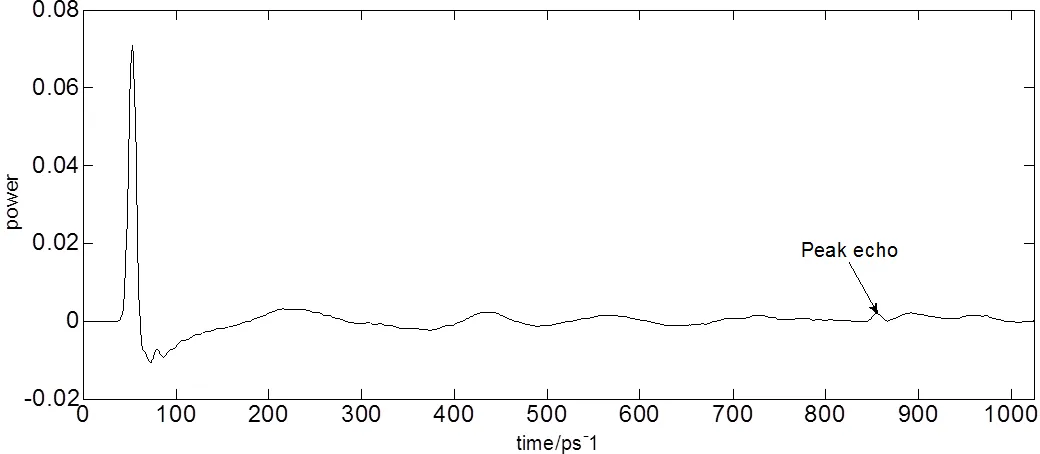
图14 脉冲响应函数（未处理）

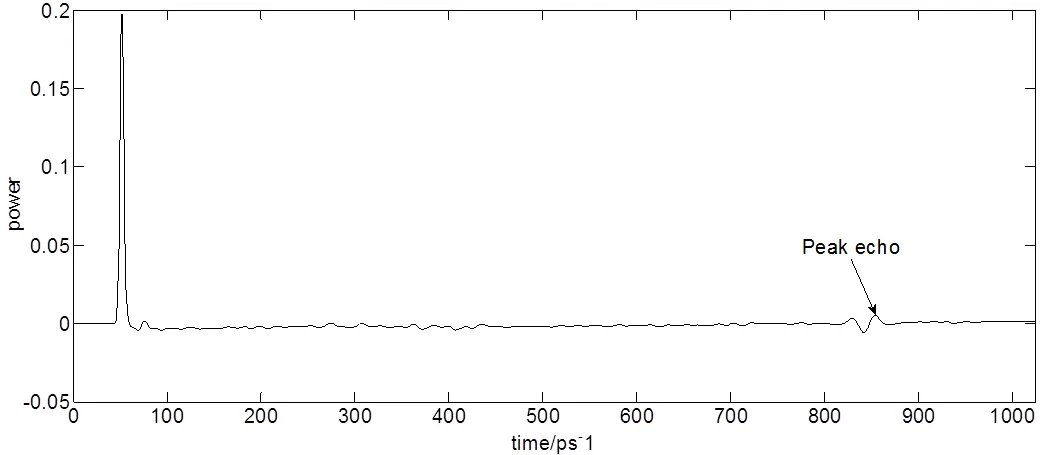
图15 脉冲响应函数（滤波后自相关算法处理）

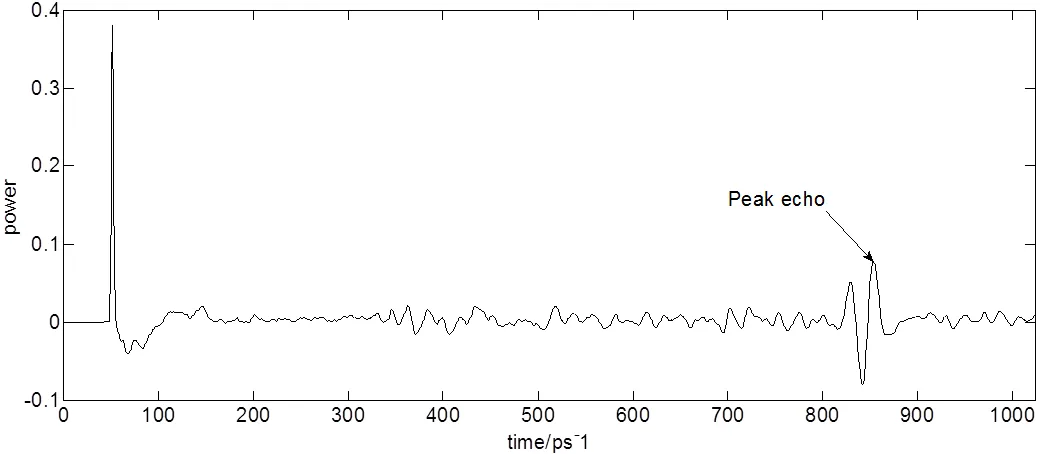
图16 脉冲响应函数（滤波后修正自相关算法处理）

4 结论

本文为解决太赫兹非金属材料测量领域时域信号表征问题。采用基于修正自相关算法的THz-TDS聚乙烯测厚反卷积算法对太赫兹聚乙烯材料厚度测量时域数据进行信号处理。本算法通过对带通滤波后的时域信号采用自相关算法进行自相关性分析，再结合高斯滤波反卷积运算，得到改进后的脉冲响应函数。改进算法实验结果显示加强了信号的清晰度，解决了因杂波信号干扰造成的脉冲响应信号失真或淹没情况，显著提高了脉冲响应信号信噪比。有效解决了高斯反卷积算法直接应用于非金属太赫兹测量时域信号处理无法有效提取信号时域特征信息的问题。另外，提出一种自相关函数的修正算法，通过与自相关算法进行结果比对，明显可得自相关修正算法效果优于自相关算法，更适合时域信号的信号特征。且在实验过程中发现修正自相关函数出现信号拖尾性，需要进一步研究。

[1] 刘庆兆. 脉冲辐射场诊断技术[M]. 北京: 科学出版社, 1994.

LIU Qingzhao.[M]. Beijing: Science Press, 1994.

[2] John G P, Dimitris G M. 数字信号处理: 原理、算法与应用[M]. 张晓林, 译. 北京: 电子工业出版社, 2004 .

John G P, Dimitris G M.[M]. Translated by ZHANG Xiaolin. Beijing: Electronics Industry Press, 2004.

[3] Duvillaret L, Garet F, Coutaz J. Highly precise determination of optical constants and sample thickness in terahertz time-domain spectroscopy[J]..., 1999, 38(2): 409-415.

[4] 王秀敏. 太赫兹光谱分析中用误差理论确定样品厚度的研究[J]. 激光与红外, 2009, 39(8): 884-886.

WANG Xiumin. Study on the determination of sample thickness using error theory in terahertz spectrum analysis[J]., 2009, 39(8): 884-886.

[5] 李丽娟, 周明星, 任姣姣. 基于太赫兹时域光谱的胶层厚度均匀性检测[J]. 激光与红外, 2014, 44(7): 801-804.

LI Lijuan, ZHOU Mingxing, REN Ye. Detection of uniformity of adhesive layer thickness based on terahertz time domain spectroscopy[J]., 2014, 44(7): 801-804.

[6] 陆庆华, 陈玉洁, 严盈富. 薄膜包衣厚度测量方法分析[J]. 南昌航空大学学报, 2014, 28(4): 76-82.

LU Qinghua, CHEN Yujie, YAN Yingfu. Analysis of measurement methods of film coating thickness[J]., 2014, 28(4): 76-82.

[7] 寇宽, 赵国忠, 刘英. 利用太赫兹时域光谱同时确定样品厚度和折射率[J]. 中国激光, 2015, 42(8): 0815001.1-081500.6.

KOU Kuan, ZHAO Guozhong, LIU Ying. Simultaneous determination of sample thickness and refractive index using terahertz time domain spectroscopy[J]., 2015, 42(8): 0815001.1-081500.6.

[8] 刘子烨, 刘建军, 洪治. 基于光子混频连续太赫兹波的厚度检测[J]. 激光技术, 2016, 40(4): 496-499.

LIU Zizhen, LIU Jianjun, HONG Zhi. Thickness detection of continuous terahertz waves based on photon mixing[J]., 2016, 40(4): 496-499.

[9] Zeiler MD, Krishnan D, Taylor GW, et al. Deconvolutional networks[C]//(),, 2010: 2528-2535.

[10] Zeiler M D, Taylor G W, Fergus R. Adaptive deconvolutional networks for mid and high level feature learning[C]//(),, 2011: 2018-2025.

[11] 蔡川, 李旭光, 尹毅, 等. 空间电荷测量信号恢复中的频域反卷积技术及实现[J]. 电工技术学报, 2009, 24(10): 165-169.

CAI Chuan, LI Xuguang, YIN Yi, et al. Frequency domain deconvolution technology and implementation in space charge measurement signal recovery[J]., 2009, 24(10): 165-169.

[12] 吴超一, 钟力生, 王霞, 等. 脉冲电声法空间电荷测量波形恢复的数据处理[J]. 中国电机工程学报, 2005(16): 137-140.

WU Chaoyi, ZHONG Lisheng, WANG Xia, et al. Data Processing of Waveform Recovery of Pulsed Electroacoustic Space Charge Measurement[J]., 2005(16): 137-140.

[13] Tanaka Y, Hanawa K, Suzuki K, et al. Attenuation recovery technique for acoustic wave propagation in PEA method[C]//,2001, 2001: 407-410.

[14] 刘明亮, 蔡永泉, 饶敏, 等. 用卷积运算实现反卷积[J]. 电子学报, 2000(5): 111-112.

LIU Mingliang, CAI Yongquan, RAO Min, et al. Deconvolution with Convolution Operation[J]., 2000(5): 111-112.

[15] 邱程, 付红卫, 王欣, 等. 反卷积算法在超宽带时域测量中的应用[J]. 探测与控制学报, 2013, 35(3): 80-84.

QIU Cheng, FU Hongwei, WANG Xin, et al. Application of deconvolution algorithm in ultra-wideband time domain measurement[J]., 2013, 35(3): 80-84.

[16] Parruck B, Riad S M. An optimization criterion for iterative deconvolution[J]., 1983, 32(1): 137-140.

[17] 扈罗全, 郑飞虎, 张冶文. 用于电介质中空间电荷分布测量的Tikhonov反卷积算法[J]. 计算物理, 2004(5): 432-438.

LUO Luoquan, ZHENG Feihu, ZHANG Yewen. Tikhonov deconvolution algorithm for measuring space charge distribution in dielectrics[J]., 2004(5): 432-438.

[18] 姚若河. 时域卷积反演的一个新算法[J]. 桂林电子工业学院学报, 1988(2): 38-42.

YAO Ruohe. A New Algorithm for Time Domain Convolution Inversion[J]., 1988(2): 38-42.

[19] 高晋占. 微弱信号检测[M]. 北京: 清华大学出版社, 2004.

GAO Jinzhan.[M]. Beijing: Tsinghua University Press, 2004.

[20] 许峰, 李开成, 王可. 一种基于相关算法的电能质量信号定位方法[J].电测与仪表, 2015, 52(3):1-5.

XU Feng, LI Kaicheng, WANG Ke. A Power Quality Signal Positioning Method Based on Correlation Algorithm[J]., 2015, 52(3): 1-5.

[21] 胡大红, 姚志鹏. 自相关函数在时间序列模型识别中的应用[J]. 襄樊学院学报, 2011, 32(5): 15-18.

HU Dahong, YAO Zhipeng. Application of autocorrelation function in time series model identification[J]., 2011, 32(5): 15-18.

[22] 刘正平, 臧观建, 陈俊杰. 微弱周期脉冲信号的自相关-混沌系统联合检测方法[J]. 噪声与振动控制, 2007(5): 63-65.

LIU Zhengping, ZANG Guanjian, CHEN Junjie. Auto-correlation-chaotic system detection method for weak periodic pulse signal[J]., 2007(5): 63-65.

[23] 吕文秋. 强噪声中周期信号的数字重相关检测[J]. 厦门大学学报: 自然科学版, 1990, 29(1): 34-38．

LYU Wenqiu. Digital recorrelation detection of periodic signals in strong noise[J].: Natural Science Edition, 1990, 29(1): 34-38.

[24] 范晓志, 王长广, 黄晓红, 等. 基于小波分析和多重自相关法的微弱信号检测技术[J]. 计算机应用与软件, 2007, 24(5):40-41, 44.

FAN Xiaozhi, WANG Changguang, HUANG Xiaohong, et al. Weak signal detection technology based on wavelet analysis and multiple autocorrelation methods[J]., 2007, 24(5): 40-41.

Deconvolution Algorithm of THz-TDS Polyethylene Thickness Measurement Based on Modified Autocorrelation Algorithm

JIANG Qiang1,2，YU Yue3，YE Lingwei1,2，HAO Yuan4

(1. Zhejiang Special Equipment Science Research Institute, Hangzhou 341000, China; 2. Zhejiang Key Laboratory of Special Equipment Safety Testing Technology Research, Hangzhou 341000, China;3. China Special Equipment Inspection Institute, Beijing 100029, China; 4.China Measurement University, Zhejiang 310018, China)

In polyethylene pipe manufacturing processes, the precise measurement of the pipe thickness is an important technical problem, which affects the quality of the pipes produced. In the terahertz non-metal thickness transmission measurement process, the sample thickness parameter is obtained by measuring the optical path time difference of the two transmitted signals and material refractive index. To accurately extract the optical path time difference of the two transmitted signals, signal characterization of the original time domain signal is required, which is a mature and effective technical means to characterize the signals impulse response functions. An impulse response function can be obtained using a deconvolution technique. However, when the echo signal is weak or the system signal-to-noise ratio is low, the interference signal increases, causing distortion and flooding of the signal, and thus, the signal cannot be accurately extracted. In this study, we first pre-process the time domain signal with a Butterworth filter and perform an improved self-precision analysis on the processed signal. Second, we perform Gaussian deconvolution processing for autocorrelation signals. Finally, we obtain an improved impulse response function. The improved method aims to solve the problem of signal characterization in the field of terahertz non-metal measurement. The improved algorithm enhances the clarity of the signal and solves the distortion or flooding of the impulse response signal caused by the interference of the clutter signal. Consequently, the signal-to-noise ratio of the impulse response signal is improved.

terahertz, Gaussian filter deconvolution, signal characterization, improved autocorrelation function, signal to noise ratio

TB324

A

1001-8891(2020)05-0473-10

2019-04-14；

2020-04-02.

蒋强（1992-），男，硕士，主要从事太赫兹无损检测技术与信号处理。E-mail: 1125138001@qq.com。

国家重点研发计划项目（2017YFF0209704）。