吸气式高超声速飞行器爬升段关键任务点的鲁棒优化

汤佳骏，刘燕斌，曹 瑞，陆宇平，朱鸿绪，衣春轮

(1. 南京航空航天大学自动化学院， 南京 210016； 2. 南京航空航天大学航天学院， 南京 210016；3. 北京航空航天大学虚拟现实技术与系统国家重点实验室， 北京 100191)

0 引 言

吸气式高超声速飞行器因其较高的潜在应用价值，已成为各国争相研究和发展的技术热点。吸气式高超声速飞行器良好的气动/推进一体化设计满足了设计人员对飞行器气动/推进性能的综合需求。然而，吸气式高超声速飞行器特殊的几何构型带来的气动/推进耦合加上严苛的超燃冲压发动机工作条件，导致其呈现出非线性、强耦合及高度不确定性的复杂动力学特性，给飞行器的轨迹及控制设计提出了挑战[1-2]。

吸气式高超声速飞行器的飞行任务历经多个阶段，飞行器由机载水平发射后，经历引射和火箭模态加速爬升，到达一定的高度和速度时，切换到超燃冲压模态加速爬升到期望的任务窗口[3]。吸气式高超声速飞行器的飞行任务包线大，气动/推进特性与飞行状态存在耦合关系，飞行器在不同空域的气动特性相差很大，飞行状态的选取对模型特性影响显著[4]。爬升段始末的飞行状态，是飞行任务切换的关键节点，节点处的飞行性能对整体飞行任务会带来影响[5]。因此，综合考虑整体飞行任务，需要在轨迹设计之前对爬升段始末的关键任务点进行优化选取，得到的关键任务点可以为轨迹及控制设计提供基础。

近年来针对吸气式高超声速飞行器爬升段的研究一直在持续进行[6-11]。文献[6] 针对吸气式高超声速飞行器，以爬升消耗燃料质量最小为目标，利用序列二次规划算法求解最优航迹；文献[8] 研究了吸气式高超声速飞行器多约束下的爬升段轨迹优化问题；文献[11] 应用高斯伪谱法获得了控制约束条件下的高超声速飞行器最优爬升轨迹，并针对轨迹采用线性二次调节器理论设计了轨迹跟踪控制器。以上研究多关注爬升飞行过程，注重轨迹及控制方法的探索，而对于爬升段的关键任务点主要依靠经验直接给出，理论分析较少，对其进行研究具有较为重要的意义。一般情况下，飞行器爬升段末端往往与巡航飞行任务衔接，爬升段末端任务点可以依据巡航性能约束来进行选取。文献[12] 对吸气式高超声速飞行器巡航飞行的飞行速度进行了分析优化，但缺乏结合爬升等飞行阶段的综合考虑，模型特性也较为简单，未涉及气动/推进特性的耦合。文献[13] 针对上升段给出了高超声速飞行器最大航程的巡航任务点。文献[3] 以燃料最省对高超声速飞行器的爬升-巡航全局轨迹进行优化，给出了爬升末端的最佳巡航速度和巡航高度。然而，二者的研究未考虑模型参数不确定性，存在一定的局限性。综上，针对吸气式高超声速飞行器爬升段的研究主要关注轨迹设计与优化，对轨迹设计之前选取爬升始末关键任务点的研究较少，而现有的对关键任务点的研究往往以航程大小和燃料消耗等任务性能为指标，对飞行器的气动/推进耦合特性分析不足，同时没有考虑参数不确定性的影响。

针对上述问题，本文对吸气式高超声速飞行器爬升段关键任务点的优选方法进行研究。首先，由能量状态法得到飞行器的爬升走廊，结合超燃冲压发动机的工作约束确定了爬升起始任务点；其次，通过分析模型巡航飞行特性提出兼顾气动/推进效率的性能指标，得到优化的爬升末端任务点；最后，考虑飞行器质心位置不确定性，对爬升末端任务点进行鲁棒优化得到飞行任务窗口。鲁棒优化后的飞行任务窗口可以满足巡航飞行性能，同时对不确定性具有鲁棒性，有利于此类飞行器后续的轨迹及控制设计。

1 吸气式高超声速飞行器模型建立

1.1 吸气式高超声速飞行器几何构型

本文研究的对象为参考文献[14] 中的模型，该模型是基于X-43A构型建立的二维机理模型。几何构型如图1所示。

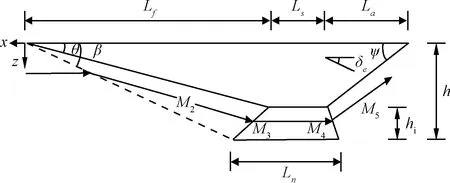
图1 吸气式高超声速飞行器几何构型Fig.1 Geometry of air-breathing hypersonic vehicle

参考模型为典型的乘波体构型，超燃冲压发动机置于机体下部，发动机的燃料为液氢。

超燃冲压发动机的工作环境处于高超声速状态，存在大量的激波、附面层以及化学反应等相关问题，发动机建模难度较大，而高超声速飞行对推力控制的实时性有一定的要求，体现在发动机模型上不能过于复杂。因此文中的推力模型参考文献[15] 对发动机内流体作一维等熵流假设，用一维可压缩流理论估算推力数据。

1.2 动力学模型

吸气式高超声速飞行器是一个复杂的动力学系统，对建模过程提出合理假设，建立飞行器纵向运动方程

(1)

式中：m和Iyy分别是飞行器质量和绕轴转动惯量，系统状态量为XT=[V,α,h,q,θ]，分别表示飞行速度，迎角，高度，俯仰角速率以及俯仰角。L，D，M，T分别表示作用在飞行器上的升力、阻力、俯仰力矩及推力。气动力和力矩的数据采用斜激波和Prandtl-Meyer flow理论的计算方法获得[16]。气动力和推力的各项导数用最小二乘法获得高精度的近似表达式，如式(2)所示。其中，δe和φ作为动力学方程中的控制量，分别表示升降舵偏转角和燃油当量比。升降舵偏转角的变化范围为δe∈[-20°,20°]，燃油当量比的变化范围为φ∈(0,1]。

(2)

吸气式高超声速飞行器的气动系数和推力系数中均包含了高度项和马赫数项，反映了模型特性与飞行状态之间的紧密关联。同时，模型气动系数CL、CD与推力系数CT的表达式中，迎角、马赫数及燃油当量比等相关项的存在，进一步考虑了模型气动和推进之间的耦合关系。图2是基于拟合表达式的气动力、推力数据与估算参考数据的对比。图2可以验证高精度的气动力及推力拟合表达式能良好地反映原始模型的特性。

图2 气动力和推力的拟合数据与估算的参考数据对比图Fig.2 Comparison of aerodynamic and thrust fitting data with estimated reference data

拟合表达式的形式方便计算，适用于快速分析，式中影响项作为参考也映证了吸气式高超声速飞行器气动/推进与飞行状态耦合，气动/推进之间也耦合的复杂本体特性。

1.3 飞行约束条件

吸气式高超声速飞行器在飞行过程中需要满足一系列的约束条件。

1)动压约束

高超声速飞行器的气动铰链力矩限制与发动机启动的要求，对飞行器所受动压有上下限值的约束，即

(3)

2)热流率约束

吸气式高超声速飞行器在飞行过程中，由于热防护的要求，飞行状态的选取需要以热流密度作为约束条件

(4)

式中：C=7.9686×10-5，Z=0.5，K=3.15。

3)控制约束

超燃冲压发动机的工作状态条件严苛，过高的燃油当量比会使发动机燃烧室内的温度增量过大，温度增量超过临界时超燃冲压发动机容易达到热壅塞而不能正常工作，故而平衡状态下的燃油当量比应满足

φequal<φchoke

(5)

式中：φchoke是超燃冲压发动机达到热壅塞时的燃油当量比。

(6)

2 吸气式高超声速飞行器关键任务点优选流程

本文主要研究吸气式高超声速飞行器爬升段关键任务点的优选问题，包括爬升起始任务点和爬升末端的飞行任务窗口的确定，研究工作主要分为三个部分：

1) 通过能量状态法确定飞行器的爬升走廊，分析发动机工作约束选取爬升起始任务点；

2) 分析模型巡航飞行的气动特性与动力特性，综合性能指标优化爬升末端任务点；

3) 在优化的参考任务点基础上考虑模型参数不确定性，结合巡航飞行约束进行鲁棒优化，得到爬升末端的飞行任务窗口。

鲁棒优化的结果得到了满足巡航飞行性能要求，同时对模型不确定性具有鲁棒性的飞行任务窗口。具体流程如图3所示，后文将按顺序阐述优选流程在本文模型上的实现。

图3 吸气式高超声速飞行器关键任务点优选流程图Fig.3 Flow chart for optimized selecting key mission point of the air-breathing hypersonic vehicle

3 选取爬升起始任务点

在高速飞行状态下，超燃冲压发动机的比冲远大于火箭，其工作效率更优，因而在飞行器整个上升段中应尽可能早的开启超燃冲压发动机，以节省燃料[17]。为选取爬升起始任务点，首先根据能量状态法确定吸气式高超声速飞行器的爬升走廊，约束任务点的可行域。

基于能量状态法[18]的分析主要考虑飞行器的纵向运动，将飞行器看作质点，其无侧滑运动方程可结合式(1)得到

定义单位质量飞行器的能量为

(8)

将式(7a)、(7c)、(7d)同式(8)联立，可得吸气式高超声速飞行器的能量状态模型

(9)

爬升段的能量变化率是大于零的，在能量变化率等于零的高度飞行器只能维持水平飞行。在给定马赫数下，计算dE/dt=0所对应的高度，可以得到飞行器允许爬升的飞行范围。文献中吸气式高超声速飞行器巡航飞行的标称质量为14.36×103kg，作为爬升段末端任务点处的质量。为保证巡航段飞行任务，文献[19] 中给出了飞行器质量与燃料质量的关系，在此假设爬升段末端任务点处的燃料质量为总量的70%，得到爬升起始状态的质量为16.68×103kg。由能量状态法结合飞行器动压约束和热流约束得到吸气式高超声速飞行器的爬升走廊，如图4中灰色区域所示。飞行器能量变化率等于零时的飞行高度，对应了飞行器爬升飞行的高度上边界，在边界以下飞行器的能量变化率大于零可以进行爬升飞行。

图4 吸气式高超声速飞行器爬升走廊Fig.4 Climbing corridor of air-breathing hypersonic vehicle

其次，在爬升走廊内分析超燃冲压发动机的工作约束选取爬升起始任务点。爬升飞行起始状态的飞行马赫数小，发动机进气道来流速度低导致发动机喷口处的气流马赫数低，容易引起发动机热壅塞而无法正常启动[20]。对于本文的超燃冲压发动机模型，燃油当量比的数值可以作为分析发动机热壅塞状态的指标，Doman给出了拟合表达式计算超燃冲压发动机达到热壅塞时的燃油当量比，其主要的影响项是来流马赫数、迎角和动压[21]。从超燃冲压发动机燃烧效率的角度考虑，动压越大其工作性能越好[22]，考虑在动压约束边界保留一定的余量，选择95 kPa作为爬升飞行的初始飞行动压。

图5显示了飞行动压95 kPa下超燃冲压发动机达到热壅塞状态的燃油当量比随来流马赫数和迎角的关系，黑色点划线是飞行动压95 kPa下的模型配平燃油当量比，可以看出选择95 kPa为初始飞行动压，当飞行马赫数较小的时候，吸气式高超声速飞行器保持平飞的燃油当量比要大于热壅塞状态的燃油当量比，即飞行器受发动机热壅塞状态限制无法保持水平飞行，从曲线交点处分析，飞行马赫数在6.5以上飞行器的配平燃油当量比大于热壅塞状态的燃油当量比，超燃冲压发动机可以正常工作供飞行器进行爬升机动。

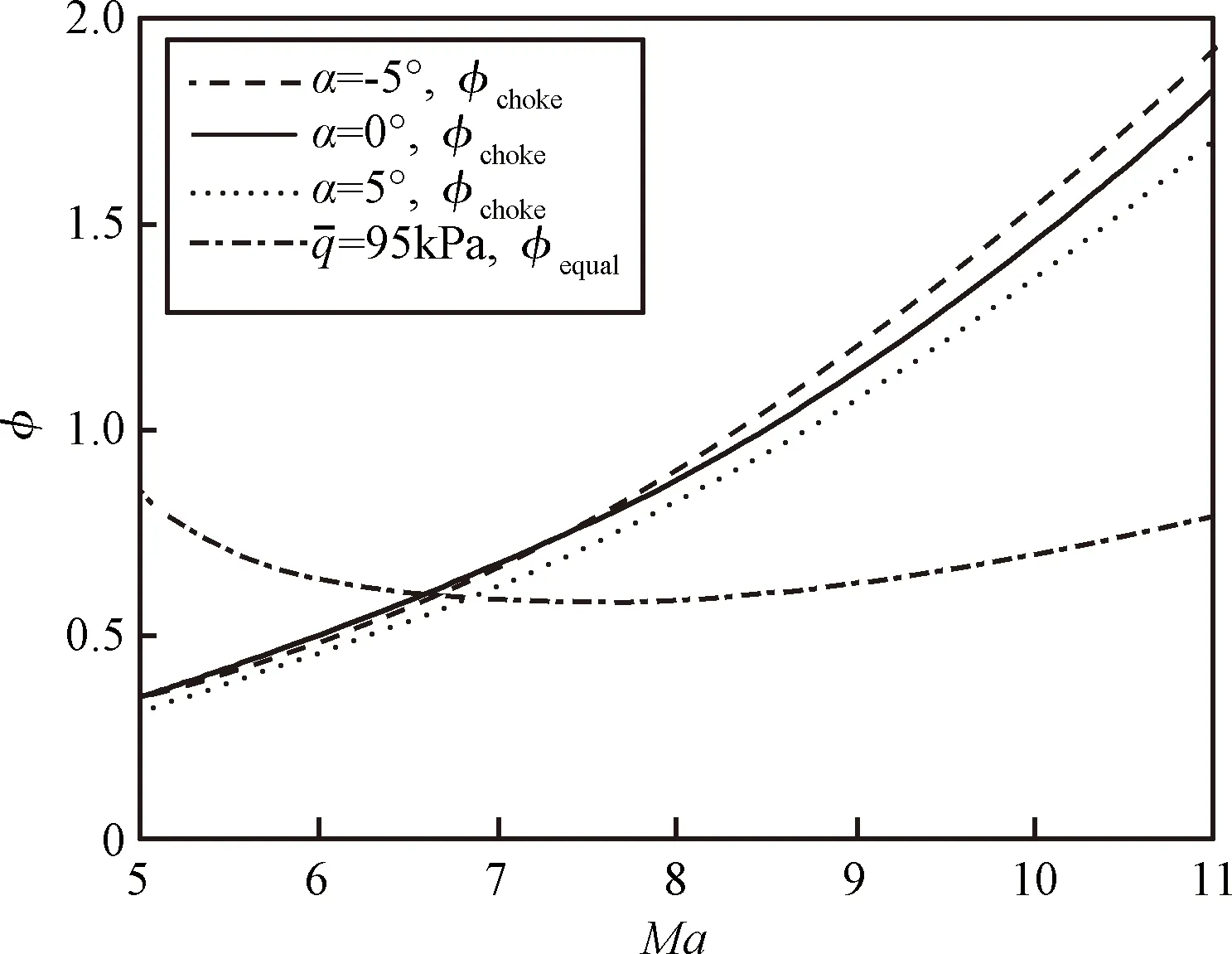
图5 飞行动压95 kPa下超燃冲压发动机达到热壅塞状态的燃油当量比随来流马赫数和迎角的关系Fig.5 The fuel equivalent ratio of scramjet engine choke versus Mach number and angle of attack for dynamic pressure of 95 kPa

综上，对本文研究的飞行器，设计爬升起始任务点的马赫数和高度为(6.5,23408 m)，如图4中圆点所示。爬升起始任务点的选取让飞行器较早的开启超燃冲压发动机，充分利用了超燃冲压发动机的性能优势进行爬升加速。同时，图4中灰色虚线是由能量状态法得到的能量等势线，从爬升起始任务点开始，飞行器的能量随着飞行高度和速度的增加而增大，选取爬升末端任务点的飞行速度和高度距起始任务点相近，意味着飞行器花费较少的能量可以完成爬升任务，节省了飞行器爬升过程中的燃料消耗，降低了飞行任务的难度。因此，爬升起始任务点的确定还为后续综合考虑飞行任务难度选取爬升段末端任务点提供了参考依据。

4 模型特性分析优化爬升末端任务点

吸气式高超声速飞行器的关键任务点需要在前文给出的爬升走廊内选取，飞行器的模型特性随爬升过程飞行状态的改变会产生较大变化，而气动/推进的耦合作用又使得对象特性更为复杂。因此，选取爬升末端任务点从优化气动效率和推进效率两方面综合考虑，分别分析飞行器巡航飞行的气动特性和动力特性，选取兼顾气动和推进效率的性能指标进行优化。

飞行器巡航飞行性能分析和优化在亚声速和超声速速域都有了一定的研究可以作为参考，但其性能指标是否适用于吸气式高超声速飞行器，需要具体分析模型特性来验证。

4.1 优化气动效率

在高超声速巡航过程中，假设飞行器的迎角很小可以忽略。同时，巡航飞行采用定高定速的飞行模式，则为了保持稳态飞行需要满足下式

(10)

升阻比是反映飞行器气动特性的重要参数，优化升阻比就是优化飞行器的气动效率。由于高超声速飞行气流的压缩性效应明显，飞行器的气动导数需要考虑马赫数的影响，由式(2)可知，阻力系数和升力系数均是迎角、舵偏和马赫数的函数，而在平衡状态约束下，平衡状态量和控制量是确定的，阻力系数可以由升力系数和马赫数的函数表示

CD=CD(CL,Ma)

(11)

吸气式高超声速飞行器升阻比最大的条件由对数微分的形式表示为[23-24]

(12)

其中，dln为对数微分的符号，根据式(11)，

(13)

定义如下的对数导数

(14)

(15)

无量纲的对数导数便于计算处理，则式(13)可以写成

dlnCD=CD,LdlnCL+CD,MadlnMa

(16)

式(12)也可以转化为

(1-CD,L)dlnCL-CD,MadlnMa=0

(17)

分析式(17)，分别固定马赫数Ma或升力系数CL时，即有dlnMa=0或dlnCL=0，可以得到升阻比最大的优化条件

(18)

(19)

当同时满足式(18)和式(19)可以得到使飞行器升阻比最大的全局最优解。根据式(13)，图6分别给出了吸气式高超声速飞行器的阻力系数随升力系数和马赫数的变化规律。从图6(a)可以看出阻力系数与升力系数的关系，模型的阻力系数随升力系数的增大而增大，这与亚声速飞行速域下阻力系数的变化规律是相似的[24]。对于给定的马赫数，模型的升阻比在阻力系数曲线与过原点直线的相切点取到最大。虚线与阻力系数曲线相交的圆点为CD,L=1 所对应的状态，这与图7(a)中的圆点相对应。而图7(b)表明，吸气式高超声速飞行器的阻力系数随马赫数的增大而减小，这与亚声速速域阻力系数随马赫数的变化规律相反[24]，而且给定升力系数下升阻比最大的优化条件CD,Ma=0在所研究的Ma=4 到Ma=11的高超声速速域范围内无解，说明指定速域的配平状态下吸气式高超声速模型的阻力系数随着马赫数的增加始终在减小，可以看出在较小的升力系数下，阻力系数随马赫数减小较快。依据曲线的走势，CD,Ma=0的优化条件需要在更高的马赫数下才能达到。另一方面，较大的升力系数下，阻力系数随马赫数的下降趋于平缓，结合图6(b)可以看出在升力系数均较大的情况下，阻力系数表现出明显的压缩性，马赫数对升阻比的影响逐渐减小，通过计算验证，给定较大升力系数，在Ma=4到Ma=11的速域内存在CD,Ma=0，然而平衡状态的控制量约束下飞行器无法满足此时的升力系数。

显然，吸气式高超声速飞行器要达到更高的飞行速度需要付出更大的代价，同时较高的飞行马赫数也超出了超燃冲压发动机的工作范围，因此CD,Ma=0这一指标对本文的模型并不适用。

图6 吸气式高超声速飞行器阻力系数变化特性Fig.6 Characteristics of drag coefficient of air-breathing hypersonic vehicle

图7 吸气式高超声速飞行器升阻比变化特性Fig.7 Characteristics of lift-to-drag ratio of air-breathing hypersonic vehicle

图8 吸气式高超声速飞行器升阻比等势图Fig.8 Contours of lift-to-drag ratio of air-breathing hypersonic vehicle

在亚声速速域中飞行器的升阻比通常随飞行速度的增大而减小[24]，但是吸气式高超声速飞行器的升阻特性呈现出不同的规律。按照之前的分析，飞行器在所研究的速域内曲线CD,L=1与CD,Ma=0没有交点，无法取到升阻比最大的全局最优解，只能按照CD,L=1这一指标寻求次优结果。图8更清晰地给出了固定马赫数时，飞行器在CD,L=1指标下升阻比最大的次优结果。

4.2 优化推进效率

在高超声速飞行条件下，超燃冲压发动机作为吸气式高超声速飞行器的动力系统，其工作状态受飞行状态变化的影响剧烈[25-26]。根据式(2)中影响项，燃油当量比、马赫数和迎角是影响超燃冲压发动机推力的主要因素。

燃油当量比是发动机模型的控制量，对推力大小有直接的影响，飞行器的燃油当量比，可以表示为

(20)

(21)

图9是超燃冲压发动机的配平燃油当量比随马赫数的变化曲线，随着马赫数的增加，燃油当量比减小，发动机提供的配平推力也在减小，平衡状态下推力与阻力近似，这与前文图6中阻力系数的变化规律相互印证。同时，相同马赫数下，随着高度的增加，大气密度会产生很大变化，空气稀薄导致空气质量流率下降，会导致燃油当量比增加，发动机易进入热壅塞状态。故而，飞行器巡航飞行应保证飞行高度较高的情况下飞行马赫数不能过小，以避免超燃冲压发动机进入饱和或热壅塞的状态。

图9 配平燃油当量比随马赫数的变化曲线Fig.9 Fuel equivalent ratio for trim versus Mach number curve

超燃冲压发动机的工作效率可以表示为

(22)

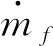
(23)

g0为标准重力加速度。故而，式(22)可以转化为

(24)

分析式(24)可知，飞行器配平状态下的发动机效率主要受发动机比冲和飞行速度影响。仿照前文的分析，可以得到超燃冲压发动机效率最大的条件为

(25)

在巡航飞行状态下，飞行高度固定，受平衡状态约束发动机的比冲近似是马赫数的函数，因而有

(26)

所以式(25)可以转化为

(27)

得到超燃冲压发动机效率最大的条件为ηMa=0。图10为超燃冲压发动机工作效率随马赫数的变化曲线，可以看出超燃冲压发动机的效率随着马赫数的增加呈现先增大后减小的变化规律，而高度变化对发动机的效率影响较小，在高马赫数段发动机效率随高度近乎不变。由ηMa=0条件，在所研究的高超声速速域内，飞行器在Ma=9～9.5速域内巡航飞行发动机的效率较高。

发动机比冲是发动机消耗单位质量的燃料所提供的推力，也可以作为衡量发动机性能的重要指标，较大的发动机比冲意味着发动机提供同等大小的推力时更为节省燃料。图11是平衡状态下超燃冲压发动机的比冲随马赫数的变化曲线。从图11可以看出,发动机的比冲随着马赫数的增加先增大后减小，比冲的曲线在高马赫数处会出现数值的剧烈下降，这是由于燃烧由当量比燃烧转为贫燃燃烧所致。考虑巡航飞行状态下超燃冲压发动机比冲最大的条件如式(28)所示。

图10 超燃冲压发动机工作效率随马赫数变化曲线Fig.10 Efficiency of scramjet engine versus Mach number curve

(28)

如图11中曲线Isp,Ma=0所示，飞行器在Ma=7.5～8.5速域内巡航飞行发动机的比冲较大。

图11 超燃冲压发动机比冲随马赫数变化曲线Fig.11 Specific impulse of scramjet engine versus Mach number curve

超燃冲压发动机的实际工作特性复杂，发动机数学模型本身存在一些简化。因此，从超燃冲压发动机的工作效率和比冲两个方面给出发动机推进效率的优化指标作为参考，分析的结果主要是优化了飞行器巡航飞行过程中马赫数的大致范围。

4.3 综合性能指标的优化结果

综合前文的分析，亚声速巡航飞行性能指标对吸气式高超声速飞行器并不能完全适用。由于模型的复杂对象特性，结合上述气动效率和推进效率两方面性能指标得到飞行任务点的优化结果。

前文得到的关于气动效率和推进效率的性能指标有CD,L=1与Isp,Ma=0、ηMa=0。图12是综合气动效率和推进效率性能指标得到的优化结果。其中，点A的马赫数和高度为(7.93,26580 m)，是综合指标Isp,Ma=0与CD,L=1的结果，其优化的目标函数相当于minf=|CD,L-1|+|Isp,Ma|；而点B的马赫数和高度为(9.72,28250 m)，是综合指标ηMa=0与CD,L=1的结果，其优化的目标函数相当于minf=|CD,L-1|+|ηMa|。结合前文选取的爬升起始任务点，点B处的飞行器能量远大于点A，从爬升起始任务点爬升到点A所经历的速度和高度变化相比于点B要小，能量变化小，故而燃料消耗量小，飞行任务较为容易，以点A作为爬升末端任务点更为合适。

图12 综合指标CD,L=1、Isp,Ma=0、ηMa=0的优化结果Fig.12 Optimization results of combining indices CD,L=1, Isp,Ma=0 and ηMa=0

综上，依据吸气式高超声速飞行器的模型特性分析，以兼顾气动效率和推进效率的优化指标对飞行器的巡航飞行性能进行优化，得到点A即为一个合适的爬升末端任务点。针对不同的飞行器、不同的飞行任务，模型的对象特性差异以及性能指标的选取不同，均会使优化分析得到关键任务点产生变化。

5 爬升末端任务点鲁棒优化

前文对爬升末端任务点的优化选取，主要是基于对飞行器模型特性的静态分析，而实际飞行中模型自身的不确定性会使模型特性产生较大的偏差，同时，优化分析没有完全考虑本体和控制等约束条件的限制，所得到的优化结果往往鲁棒性较差。故而前文所求的点A仅是模型在参数固定情况下的最优结果，在受不确定性的影响时，难以满足飞行性能具有鲁棒性的要求。针对这一问题采用鲁棒优化的思路[27]对提出的气动/推进效率性能指标做进一步改进，构造新的适应度函数，以前文选取的爬升末端任务点为参考进行优化，将任务点扩展得到邻域。邻域相比于单个状态点在轨迹设计时的鲁棒性与可实现性强，具有工程实用价值。

吸气式高超声速飞行器经历爬升段飞行，受燃料消耗、外界扰动等不确定因素影响，模型参数经历一个时变的过程，尤其是随着燃料质量的消耗，飞行器的质心位置可能发生变动，对模型本体特性产生较大影响。故本文对吸气式高超声速飞行器考虑质心位置不确定性，参考点A进行鲁棒优化得到了满足鲁棒性能指标的飞行任务窗口。

对于一个基本的优化问题，可以描述如下[27]：

s.t.x∈{xi|xlb≤xi≤xub}

(29)

其中，f(x,p)是优化的目标函数，x是由设计变量组成的向量，给出了范围约束，p是模型的一个自身参数。对于这一优化问题，不确定性会存在于设计变量x中或模型参数p中或目标函数的输出f(x,p)中。本文的优化思路主要涉及的是模型参数p不确定性影响下的优化问题。考虑不确定性的鲁棒优化问题，通过构造关于原优化目标函数f的适应度函数F来结合参数的不确定性。本文的鲁棒优化问题，可以用下面一组式子来描述

s.t.x∈{xi|xlb≤xi≤xub}

(30)

为将任务点扩展到邻域，修改式(30)描述的鲁棒优化问题的目标

(31)

其中，k为大于适应度函数Fn最小值的常数，k的设置使得优化问题变为求解最优解邻域的鲁棒次优问题，避免了求解最优问题收敛慢、陷入局部最优的风险，计算简单快速，求解式(30)的结果即为满足鲁棒性能指标的飞行区域的解集。此时，设计变量x是飞行器的飞行高度h和马赫数Ma，不确定性参数p是质心位置xcg，模型的标称质心位置在机体轴线上，在距飞行器机头16.76 m处。这里假设模型质心位置的不确定性范围为沿机体轴线方向前后变化0.5 m，即区间[16.26 m,17.26 m]。

在质心位置不确定性范围内对吸气式高超声速飞行器配平升阻比和配平比冲随高度、马赫数及质心位置的变化规律进行分析。图13中，固定飞行高度为27000 m，飞行马赫数不断增加，随着模型质心位置的增大，飞行器的升阻比单调减小。图14为标称质心位置处飞行器升阻比随高度、速度的变化趋势，结合图13和图14可以看出，质心位置的不确定性影响了飞行器的静稳定性，改变了其在平衡条件下的状态，进而对配平升阻比产生了较大的影响。而图15中，固定飞行马赫数为8，飞行高度不断增加，随着模型质心位置的增大，飞行器比冲基本保持不变，即模型的配平比冲受质心位置不确定性的影响较小。图16显示了标称质心位置(xcg=16.76 m)处发动机比冲随速度、高度的变化趋势，比冲基本随马赫数增加先增大后减小，随高度增加而减小。

图13 配平升阻比随质心位置变化规律Fig.13 Trend of lift-to-drag ratio for trim versus the position of centroid

图14 标称质心位置下配平升阻比随飞行状态的变化规律Fig.14 Trend of lift-to-drag ratio for trim versus the flight state at nominal centroid position

图15 配平比冲随质心位置变化规律Fig.15 Trend of specific impulse for trim versus the position of centroid

图16 标称质心位置下配平比冲随飞行状态的变化规律Fig.16 Trend of specific impulse for trim versus the flight state at nominal centroid position

根据第4.3节点A的性能指标可以得到优化问题的目标函数为

f((h,Ma),xcg)=λ1|CDL-1|+λ2|Isp,Ma|

(32)

其中，λ1和λ2是权值系数。对式(32)采用鲁棒正则化方法，构造如下的适应度函数

λ2|Isp,Ma|)φ(δ)dδ

(33)

式中:δ是不确定性下质心位置关于标称位置的偏移量，而φ(δ)是质心位置关于标称位置偏移量的概率密度函数。

前文优化的关键任务点A在标称质心位置下适应度函数值最小，其应在鲁棒优化问题最优解的邻域内，故而k值可以由点A处的适应度函数值放大合适的倍数确定。根据不确定性参数与性能指标的关联分析选取合适的权重系数λ1和λ2，以衡量不确定性对指标的影响程度。为了方便计算，将质心位置的不确定性范围归一化至[-1,1]区间内，-1代表质心位置前移0.5 m，1代表质心位置后移0.5 m。不确定性参数的概率分布是鲁棒优化方法的核心，但缺点是实际问题中的不确定性的概率分布不易获得。本文假设飞行器在爬升段末端的燃料消耗对质心位置的不确定性满足均值为0，方差为1/9的正态分布，则根据正态分布的理论，可以保证质心位置有99.7%的概率落在[-1,1]区间内。

(34)

结合式(30)、式(33)和式(34)，求解满足鲁棒性能指标的飞行区域，即图17中黑色虚线框所围区域。进一步考虑飞行器飞行过程中的约束条件，在爬升走廊内缩小飞行器巡航飞行的约束区域，最终的飞行任务窗口应是二者的交集。

图17在飞行器标称质心位置下的配平升阻比等势图中，对比了鲁棒优化的解集域与巡航约束区域。图中左上角的空白区域是由于模型控制量限制造成的未配平区域。飞行器的动压约束与热流约束同前文所述，而控制约束方面，燃油当量比作为发动机控制量，其饱和约束由未配平区域体现；粗实线代表了发动机的热壅塞约束。对于模型舵面偏转角，假设保留约33.3%的控制裕度，取偏转的余量为δeM=7°，则配平舵面偏转角要小于13°。最后，针对本文的吸气式高超声速飞行器，以模型配平升阻比大于3.8为约束，得到标称质心位置下的巡航约束区域为图中浅灰色区域。

图17 鲁棒优化解集域及标称质心位置下的巡航约束区域Fig.17 Solution domain of robust optimization and constrained area of cruise at the nominal centroid location

巡航约束区域的大小在质心位置不确定性影响下也会发生改变，图18中浅灰色区域为飞行器质心位置在17.26 m处的巡航约束区域，对比图17和图18可以看出,质心位置向后移动使升阻比等势线和舵偏约束发生较大变化，进而导致约束区域明显减小。同时，飞行器质心位置在17.26 m处是不确定性范围的边界，此时巡航约束区域最小，是质心位置不确定性的最坏情况。爬升末端任务点需要同时满足鲁棒性能指标要求和质心位置不确定性的最坏情况的约束，即飞行任务窗口为鲁棒优化解集域与最小巡航约束区域的交集，如图18中深灰色区域所示。

图18 飞行任务窗口及质心位置在17.26 m处的巡航约束区域Fig.18 Flight mission window and constrained area of cruise with centroid position at 17.26 m

由原先的点A扩展到飞行任务窗口，此时点A虽仍在飞行任务窗口内，但位于区域的边界处，可以选取窗口区域的中心位置点C(7.95,26350 m)为参考的爬升末端任务点，其远离飞行任务窗口的边界，鲁棒性更强。在飞行任务窗口区域内选择爬升末端任务点或直接以任务窗口为轨迹设计约束，可以满足巡航飞行性能要求，同时有效地解决可能由质心位置不确定性引起的控制饱和问题，在后续的轨迹及控制设计中更具优势和便利。

此外需要说明的是本文以质心位置这一本体参数为例说明了关键任务点到飞行任务窗口的鲁棒优化流程，飞行器实际飞行过程中受气动热、风干扰影响还存在气动、推进等诸多不确定性因素，气动不确定性会关联模型的升阻特性、舵偏约束等，而推进不确定性主要关联模型的燃油当量比、比冲等推力相关项，综合考虑两者会同时影响优化问题的性能指标和约束条件，对不确定性因素的考虑越充分得到的性能指标就越复杂，同样采用上述思路得到的飞行任务窗口必然产生差异，但鲁棒性更强，有待进一步研究。

6 结 论

1) 本文主要研究吸气式高超声速飞行器爬升段关键任务点的优选问题，包括爬升起始任务点确定和爬升末端飞行任务窗口的鲁棒优化。优化流程顺序递进，避免循环迭代；过程多是基于模型平衡状态的分析，鲁棒优化步骤求解最优解的邻域而非最优解，计算简单快速，适用于吸气式高超声速飞行器设计初期的模型外形分析、快速轨迹优化，为此类飞行器后续的轨迹及控制设计提供参考。

2) 吸气式高超声速飞行器在高超声速速域的升阻特性相比亚声速呈现出相反的变化规律，超燃冲压发动机的工作约束较为严苛，飞行器的气动和推进还存在耦合，为此充分考虑模型特性，提出了兼顾气动/推进效率的优化性能指标。

3) 在爬升过程中，吸气式高超声速飞行器的燃料质量消耗带来的质心位置不确定性对模型本体特性产生影响，通过构建鲁棒优化问题得到飞行任务窗口，提高了飞行性能的鲁棒性。以飞行任务窗口作为边界约束进行轨迹设计的可实现性强，结果更具工程实用性。