异构云系统中预算成本约束下高效的工作流调度算法

张龙信，王 兰，肖满生，文志华，李肯立

1(湖南工业大学计算机学院，湖南株洲412007)

2(湖南大学信息科学与工程学院，长沙410082)

1 引 言

万物互联时代到来，每日产生的数据量剧增，同时，人工智能、自动驾驶［1］、交通状态预测、海量数据的处理对云计算等高性能计算中心提出了更高的要求［2］.目前广泛使用的Spark 框架，在工业界和学术界备受青睐，有力地促进了高性能计算的应用［3］.

在云计算系统中，服务提供商和用户之间的利益存在一定的冲突，服务等级协议常用来管理协议双方［4］.金瑜等人系统地分析了云计算中心的信任机制，以提升用户对云计算的信心［5］.李涛教授等人基于表调度和任务复制的思想，提出了一个低时间复杂度、高效的依赖比绑定的最早完成时间优先算法，这进一步提升了异构分布式系统中并行任务调度的效率［6］.随着云计算商用模式的成熟，文献［4］提出了一种面向市场的云工作流多层次调度策略，具体包含任务到服务的服务级调度处理，本地云数据中心中任务到虚拟机(VM)分配的任务级调度，并提出三种复杂度较高的元启发式算法.对于云服务提供者而言，他们希望在最短的时间内完成用户提交的计算任务［7-9］.而对用户而言，他们向云计算中心支付任务计算的成本是其非常关心的重要指标之一.朱亚会等人设计了基于资源利用率的虚拟机调度模型，并为此模型提出了一种自适应的粒子群优化算法进行求解［10］.李薛剑和李凯针对传统调度静态优先级的不足，提出了一种动态优先级的作业调度策略，以兼顾任务的优先级和公平性［11］.在云计算环境中，截止期限约束下的并行任务集调度研究引起了学者们的兴趣.文献［12］基于虚拟机同构的云计算中心，提出了截止时间约束下的并行任务集资源消耗最小的调度算法.文献［13］在考虑通信竞争情况下提出了异构分布式系统中高效的并行任务集可靠性调度算法.文献［14］基于云计算与移动网络，提出一种工作流任务集调度性能和能耗联合优化算法，以提高移动云中的网络服务质量和效率.

近年来，围绕预算约束下并行任务集的调度长度最小化目标，国内外的学者们展开了广泛的研究［15-18］.这些工作中，比较典型的是异构预算成本调度算法(HBCS［17］)和预算等级最小化调度长度算法(MSLBL［18］).HBCS 首先保证并行任务集中的每个任务最小的计算开销，确保每个任务在最坏的情况下依然能以最低的预算成本分配至处理器上执行.用户预算与并行任务集中所有任务节点的最低保障执行成本之差，本文中称之为松弛成本.当候选任务等待执行时，HBCS算法根据价值函数(worthiness)分配处理器，计算成本开销，任务分配完再更新松弛成本.HBCS 算法较好地解决了预算约束下的并行任务调度问题，然而其基于价值函数分配处理器的规则仍有一定的局限性.文献［18］基于此，提出了著名的MSLBL 算法，调度性能进一步得到提升.MSLBL 算法首先计算任务的预算等级，从而保证每个任务的预算成本进一步接近任务在并行任务集中的优先等级，然后映射任务至虚拟机时则采用最早时间优先的调度策略［19］.无论是HBCS 在平摊思想的基础上的贪婪算法，或者是优化后的MSLBL 算法，在减少任务集的调度长度方面均有一定的局限性.本文将根据工作流图中各任务节点的综合优先等级，先确定任务的初始预算等级成本，当任务进入候选就绪状态时，根据当前的松弛成本增加其预算开销;在选择虚拟机执行阶段，工作流图中的关键节点在不超过任务预算成本的前提下，优先分配至关键虚拟机(执行关键路径上的所有任务所需时间最少的虚拟机).基于此思想，可以在满足用户指定预算成本的前提下，更大程度地保障工作流图中每一个任务节点选择其最佳的执行虚拟机，并可以进一步降低任务集的调度长度.

2 相关知识

2.1 云计算中的工作流任务调度

异构云计算系统中的任务调度模型包含三层:云基础设施层，云资源管理层，以及工作流任务图层.云基础设施层主要包含互联的计算节点组.资源层主要包含配置不同的VM组，它们之间通过高速网络连通形成强大的云资源池.工作流任务图层为用户提交至云计算中心的各类复杂的具体应用，工作流图中的任务之间存在着一定优先顺序约束.云计算中的工作流任务调度问题，本质上是为提交至云计算中心的具体应用选择合适的虚拟机资源，将其中的每个任务在满足一定的约束条件(优先顺序约束、预算成本约束等)下分配至选择的虚拟机，以期在较短的时间内(或者在预算成本约束的条件下等)得到最后的运行结果.

2.2 应用模型描述

本文的目标计算平台由一组计算能力和计算开销各异的虚拟机资源池组成，其中的虚拟机节点的计算、存储、网络能力各异.虚拟机资源池用 VM={vm1，vm2，…，vmv}表示，其中|v|为虚拟机节点的数量.工作流任务集通常可以用有向无循环图(DAG)进行描述，用 G(T，E，C，W)表示，其中 T 为节点任务集合，E 为DAG 中直接相连两任务节点的边集合，C 为直接相连两节点之间通信边的集合，W 为节点任务在不同的虚拟机上的计算开销集合.对于DAG 中任意直接相连的两个任务节点τi，τj，当 ei，j∈E，ei，j表示 τj不能先于 τi执行.只有当任务 τi执行完，且任务 τj所依赖的其它数据准备就绪才能被执行.ci，j(ci，j∈C)表示任务τi的数据输出至τj所在的虚拟机所需要的通信时间，当且仅当 τi，τj在同一个虚拟机上执行时，ci，j才为零.wi，j表示任务τi分配在虚拟机vmj上执行所需要的计算开销.本文中任务节点τi的直接前驱节点集合记为parent(τi)，直接后继节点集合记为child(τi).对于一个给定的DAG 工作流任务集，如果节点的直接前驱节点集合为空，则称该节点为入口节点，记为τentry.如果一个节点的后继节点集合为空，则称该节点为出口节点，记为τexit.本文约定，所研究的DAG 工作流任务集中入口节点和出口节点有且仅有一个.当用户提交的工作流任务集不符合此约定时，可以通过增加零计算开销的虚拟入口/出口节点，同时增加零通信开销的虚拟通信边与已有的DAG 图相连，以达到上述约定.

如图1 所示，这是一个典型的工作流任务图，其中包含了11 个任务节点.表1 为图1 中各任务节点在3 组不同的虚拟机上的计算开销表.以τ2为例，只有当其直接父亲节点τ0执行完，τ2才可能进入准备就绪状态.当 τ0与 τ2不在同一个虚拟机上执行时，此时的通信开销c0，2为 12.在表1 中，w2，1表示 τ2在虚拟机vm1上执行时的计算开销，大小为12.

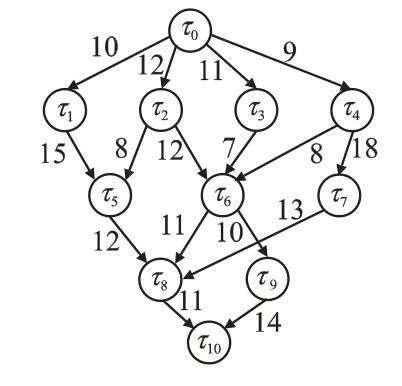
图1 一个典型的工作流图Fig.1 A classic workflow application

表1 图1 中各任务节点的计算开销表Table 1 Computation cost of task nodes in fig.1

为了下文描述方便，现给出以下相关概念的定义.

定义1.数据准备就绪时间:任务τi在虚拟机vmj上的数据准备就绪时间为任务节点τi所依赖于前驱节点数据全部准备就绪的时刻，其计算表达式如式(1)所示.

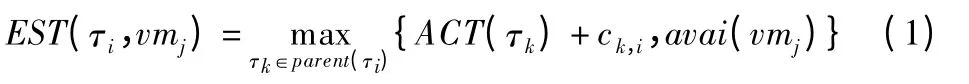
其中，ACT(τk)表示任务τk的实际执行完成时刻，avai(vmj)表示虚拟机可用的时间.

同理，τi在虚拟机 vmj的最早完成时间 EFT(τi，vmj)如式(2)所示.

定义2.向上优先等级:工作流任务的向上优先等级URank 保证任务在执行过程中的优先依赖关系，自DAG 任务集的出口节点开始递归向上进行计算.如式(3)所示，任务τi的 URank 等于其后继节点(child(τi))与 τi之间的通信开销之和的最大值加上其在所有虚拟机上的平均计算开销.

同理，任务τi的向下优先等级DRank 的计算表达式如式(4)所示.

定义3.任务的计算开销:任务τi在虚拟机上的计算开销表达式如式(5)所示，其中，wi，k为任务在虚拟机vmk上执行所需的时间，Costunit(vmk)为任务在虚拟机上运行时每单位时间所需要的成本.

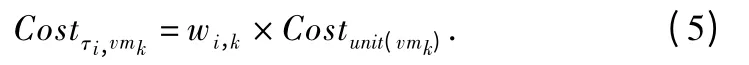
定义4.工作流任务集的计算开销Cost(G):工作流任务集的计算总开销等于各任务在所分配的虚拟机上执行开销的总和.Cost(G)的计算表达式如式(6)所示，其中 wi，map(vmk)表示任务τi在所分配的虚拟机vmk上的执行时间.

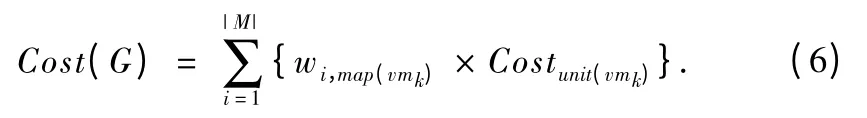
定义5.工作流任务集的最小计算开销(Costmin(G)):工作流任务集的Costmin(G)为各任务在所有虚拟机上的最小计算开销之和.Costmin(G)计算表达式如式(7)所示，其中为工作流任务集中任务的数量.

定义6.工作流任务集的最大计算开销(Costmax(G)):工作流任务集的Costmax(G)为各任务在所有虚拟机上的最大计算开销之和.Costmax(G)计算表达式如式(8)所示.

定义7.调度长度(makespan):调度长度又可称之为SL，为工作流图中所有的任务节点调度完成时，最后一个任务的实际执行完成时刻，即ACT(τexit)，其表达式如式(9)所示.

2.3 问题描述

对于用户提交至云计算中心的工作流任务图，在满足用户预算成本的前提下，以最少的时间调度完任务是提高用户服务质量的关键指标.对于一个给定的工作流任务图G，本文将要解决的问题是在满足指定预算成本Costbgt(G)的前提下，为G 中的每个任务节点选择合适的虚拟机，以期G 的调度长度最小.

上述问题的形式化可表示为式(10)和式(11).其中vmAss(τi)代表根据所设计的算法为任务τi所分配的虚拟机.

3 基于预算等级的高效调度算法(ESBL)

异构云计算中的工作流任务集调度问题，属于组合优化的范畴，是NP 难问题.本文将提出基于预算等级的高效调度算法(ESBL).在ESBL 算法中，首先将根据各节点的优先等级确定任务的预算成本，最大程度保障关键任务节点有相对宽松的计算成本;然后为工作流图中的关键路径确定虚拟机集群中的关键虚拟机，即将关键路径上的所有任务分配至同一虚拟机上执行，所需计算时间最少的虚拟机;其它任务节点将根据该节点更新后的预算开销选择最早完成时间的虚拟机.相关的定义如下:

定义8.任务的预算等级(BL):预算成本的松弛部分将根据任务的BL 进行分配，任务τi的BL 计算表达式如式(12)所示，在式(12)中，分母为工作流中所有任务节点的URank和DRank 之和.

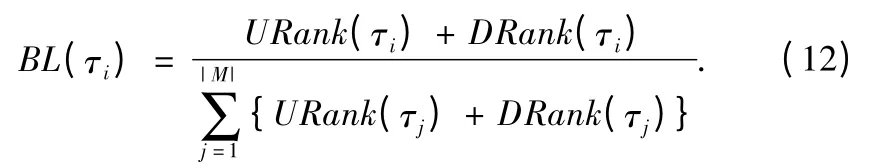
定义9.任务的预算等级开销:工作流中的任务τi在本文中初始给定的预算等级开销CostBL(τi)由其最小开销Costmin(τi)和对应的预算等级BL(τi)等因素共同决定，计算表达式如式(13)所示.

3.1 满足预算约束

本文首先需要解决的一个关键问题是如何保证在满足用户给定的预算成本约束下设计一个可行的调度策略.由式(12)、式(13)不难得出，如果所有的任务均按照任务的预算等级BL(τi)分配计算成本，虽然可以保证不违反预算约束条件，但是将浪费较多的松弛成本(用户预算成本与工作流图实际计算开销之差)，因此调度效果不甚理想.为此，本文针对准备就绪的任务，重新定义其预算开销.

定义10.数据准备就绪任务的预算开销:数据准备就绪的任务在准备执行前，为其分配的预算开销的计算表达式如式(14)所示.其中，第一个求和表达式为已经分配执行的任务实际产生的计算开销成本，第二个求和表达式为其它尚未执行的任务的预算等级开销之和.

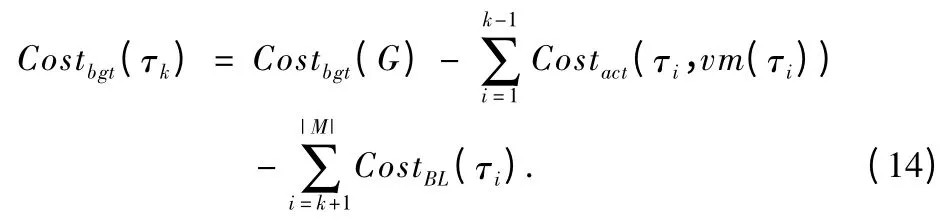
根据式(14)，在已经保证任务集中后续未执行的任务预留预算等级开销的前提下，可最大限度为准备就绪任务利用任务集当前的松弛成本，选择一个最佳执行虚拟机.

每个任务执行完都需要更新任务集最新的开销，为此，任务的松弛成本定义如下.

定义11.任务的松弛成本:任务τi的松弛成本为其预算开销Costbgt(τi)与实际开销Costact(τi)之差，如式(15)所示.

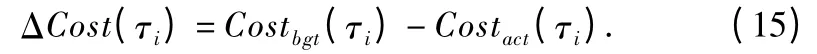
3.2 ESBL 算法

ESBL 算法的伪代码如算法1 所示.在算法1 中，步骤1和2 分别递归计算工作流图G 中各节点的DRank 和URank值.步骤3 确定G 中的关键路径节点.步骤4 确定关键节点虚拟机vmCP，即在所有虚拟机中，关键路径节点计算时间之和最小的虚拟机.

步骤5-步骤8 为每个任务节点计算其最小的计算成本Costmin，最大计算成本Costmax以及节点的预算等级BL.步骤9根据每个节点的优先等级，计算节点的预算开销CostBL.步骤10 计算工作流图G 计算成本的最小下限Costmin(G)和宽松下限Costmax(G)，即用户给定的预算成本不能低于最小下限，否则不可能调度完成.在步骤11 中，根据步骤2 得到每个节点的URank 值，根据URank 值降序排列得到队列Qr(G)，即为G 中任务的优先调度顺序.步骤12-步骤27 为ESBL 算法的核心逻辑部分.步骤13-步骤14，先从优先队列Qr(G)中取出队头节点，再计算该节点的预算开销.在步骤15 中若判断出该候选节点为G 中的关键路径节点且其在vmCP上的计算开销不大于其预算开销，则将该节点分配至vmCP.对于不满足步骤15 中条件的关键路径节点和非关键路径上的任务节点，在步骤18-步骤24 中依次遍历每个虚拟机，首先在步骤19 中计算出该节点在当前虚拟机上的计算成本，然后计算该节点在当前虚拟机上的最早完成时间，再执行步骤21-步骤23，在满足节点预算开销的约束下选择最早完成时间的虚拟机.至此，队头节点的调度完成.因此在步骤26 更新实际产生的计算开销成本，并移除队头节点，从而为下一个候选节点做好准备.当所有的节点都完成调度时，在步骤28-步骤29 分别计算出G 的实际开销成本和调度长度.

3.3 ESBL 算法时间复杂度分析

在算法1 中，对于一个具有|M|个任务节点的工作流图和|V|个虚拟机的资源池，步骤1 和步骤2 的时间复杂度均为O(|M|×|V|)，步骤9 和步骤10 的时间复杂度也为O(|M|×|V|).步骤18-步骤24 中消耗时间最多的主要是计算节点的最早完成时间，这些步骤时间复杂度为O(|M|×|V|)，所以步骤12-步骤24 的时间复杂度为O(|M|2×|V|).不难得出，算法1 的时间复杂度为O(|M|2×|V|).

3.4 ESBL 算法调度实例

如前文介绍的工作流图1，由表1 中各任务节点在虚拟机上的计算开销以及表2所示的虚拟机单位计算成本，根据式(7)可得到工作流图的最小计算开销为Costmin(G)=635.当用户给定的预算成本为650 时，根据算法1 可计算得到如表3 所示的信息，其中包含节点的 DRank，URank，CostBL以及节点执行的优先顺序等.不难看出，图1 中的关键任务节点为τ0，τ4，τ7，τ8，τ10，工作流图的优先任务队列 Qr(G)中任务的执行顺序为{τ0，τ4，τ1，τ2，τ3，τ6，τ7，τ5，τ9，τ8，τ10}.

表2 虚拟机单位计算成本Table 2 Unit price of VM

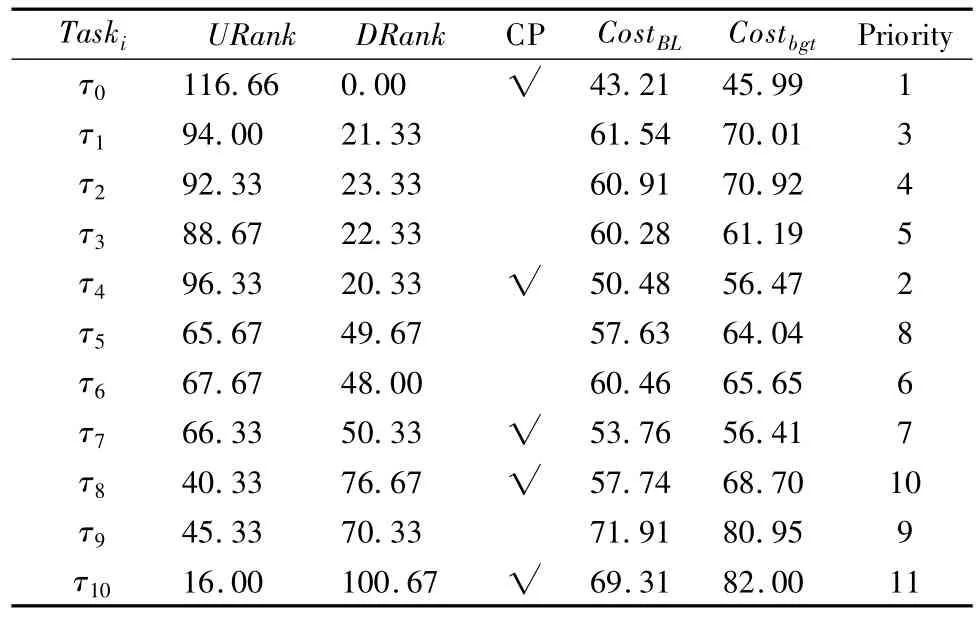
表3 根据ESBL 算法得到的图1 中各节点信息Table 3 Information of each node in fig.1 under ESBL

使用ESBL 算法调度图1 中工作流图的效果如图2 所示.工作流图产生的实际成本为633，调度长度为105.而在同样的约束下，工作流图1 采用MSLBL 算法产生的实际成本为639，调度长度为133.不难得出，本文提出的ESBL 算法在调度长度方面降低了28.

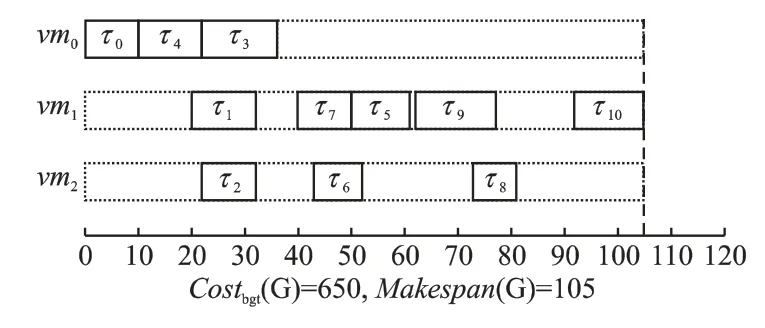
图2 工作流图1 使用ESBL 算法调度效果图Fig.2 Scheduling of fig.1 by using ESBL algorithm

4 实验部分

由于本文中提出的ESBL 算法与著名的MSLBL 算法具有相同的应用模型和系统模型，这部分将与MSLBL 算法进行对比，分析算法的性能.

4.1 实验环境

本文的实验环境参考文献［18］，将使用相同的实验环境来模拟真实应用场景.实验中使用的工作站配备了Intel Core i7-9700 @3.6 GHz 八核处理器，32 GB 内存，系统的运行版本为Win 10，并使用Java 作为实验的开发语言.实验中模拟的异构云计算系统拥有128 个计算能力和单位计算成本各异的处理器，其中处理器的类型和定价标准参考亚马逊弹性计算云(EC2［20］).本文中处理器和工作流应用中的主要参数为:处理器单位计算成本0.01 $ /h≤pricek≤1 $ /h;任务在处理器上的计算时间0.01 h≤wi，k≤128 h;工作流任务图中直接相连的两个任务之间的通信时间为0.01 h≤ci，j≤30 h.实验中使用的工作流任务图中的任务数量在32 至2048 之间.

4.2 实验评价指标

对于满足给定预算成本约束下的工作流任务调度问题，实验中采用工作流任务图实际的计算成本Cost(G)和最终的调度长度SL(G)这两个主要指标来评价本文提出的ESBL 算法和与其对比的MSLBL 算法.

为了更好地验证ESBL 和对比算法的性能，本文将采用两种典型的具有优先约束关系的并行任务集.一种为快速傅里叶变换(FFT)并行应用，另一种为高斯消元(GE)并行应用.这两种都是高性能计算领域中广泛使用的真实应用并行任务集.以下实验中使用的不同任务数量的工作流图，其预算成本开销大小为 1.2×Costmin(G).

4.3 FFT 并行应用

FFT 并行应用中包含大量递归调用和蝶形计算操作的任务节点，这类并行应用的并行度较高，在实验中需要增加一个零计算开销的伪节点作为FFT 工作流图的τexit.任务数量随着工作流图的层数(λ)增加而增长很快，任务的数量满足:|M|=Sλ=2λ，其中 λ 为大于 2 的正整数.由表4 可以看出，FFT 并行应用规模增长非常快，数量从32(小规模)到2048(大规模)之间变化.表4 中列出的7 种不同规模的FFT 并行应用，工作流图的预算成本Costbgt(G)根据任务集的最小开销Costmin(G)乘以1.2 倍取整进行设置.

以节点数为128 为例，实验中FFT 任务集的Costmin(G)为 7048，用户以1.2 倍给出预算成本，即 8458.当使用 MSLBL 算法运行时，FFT 任务集实际产生的开销为8448，调度长度为652.在同等的条件下，使用本文提出的ESBL 算法，以8247 的成本开销完成任务集的执行，所需的调度时间为542.调度长度降低了16.87%.由表4 不难看出，与MSLBL 算法相比，ESBL 算法在不增加实际成本开销的前提下，显著地减低了FFT 并行应用的调度长度.FFT 并行应用的并行度较高，表4 中的7 种不同规模的测试工作流图，在减少SL(G)方面，ESBL 算法比MSLBL 算法平均提升了17.22%.

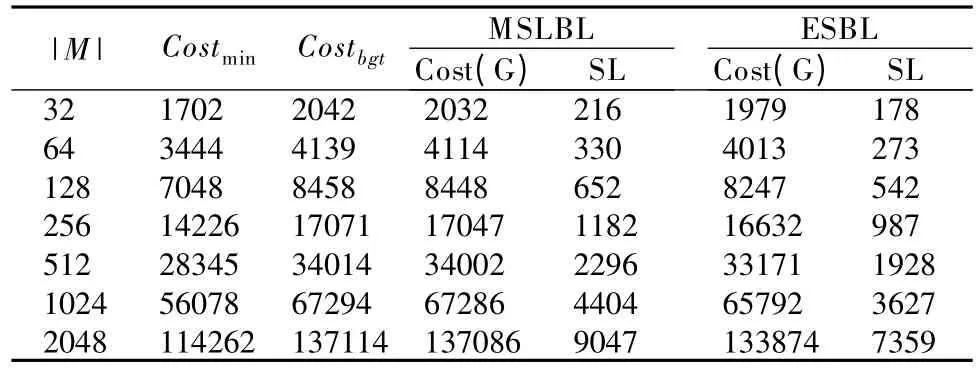
表4 不同任务数量的FFT 并行应用的算法性能对比Table 4 Algorithm performance comparisons for FFT parallel applications with different number of tasks

4.4 GE 并行应用

为了更好地验证算法的性能，第二类用于测试的数据流图为现实世界的真实GE 并行应用.高斯消元并行应用节点的数量(|M|)随着节点层数的增加满足:|M|=Sλ=(λ2+λ－2)/2，其中λ 为高斯消元矩阵的维数.

表5 不同任务数量的GE 并行应用任务图的算法性能对比Table 5 Algorithm performance comparisons for GE parallel applications with different number of tasks

如表5 所示，GE 并行应用中任务数量增长较快.以节点数为252 为例，实验中GE 并行应用的Costmin(G)为10791，用户以1.2 倍给出预算成本，即 12949.MSLBL 算法测试此GE 并行应用时，产生的成本开销为12925，调度长度为1041.而使用本文的ESBL 算法，同样的实验条件下，产生的成本开销与调度长度分别为12614 和919.此时，ESBL 算法比MSLBL 算法在减少调度长度方面提升了11.72%.GE 并行应用的并行度没有FFT 并行应用高.表5 列出了实验中使用的7种不同规模的GE 并行应用，ESBL 算法在不增加实际成本开销的前提下，对应的调度长度比同等条件下的MSLBL 算法平均降低了12.11%.

5 总 结

针对成本驱动的云计算服务日趋普遍，本文基于异构的云计算平台，提出一种时间复杂度低，调度效率高的预算成本约束下的工作流调度算法ESBL.ESBL 算法根据工作流中任务的优先等级，分配预算等级成本，保证任务集满足优先顺序约束及成本约束的同时，最大限度的保障了关键节点相对宽松的预算成本，从而达到减低任务集调度长度的目的.

通过FFT 和GE 两类、多组不同规模真实世界的并行应用对比实验，与著名的MSLBL 算法相比，ESBL 既有效地减少了工作流任务集的实际计算成本，又使其调度长度平均分别降低了17.22%和12.11%.ESBL 算法较为显著地提升了异构云计算系统中成本约束下并行任务集的调度效率.