珊瑚礁上防波堤波浪爬高的数值模拟与特征分析
谭安平,赵刘群,朱良生
(1.华南理工大学 土木与交通学院,广东 广州 510640;2.中交四航局第二工程有限公司,广东 广州 510230)
1 概述
21世纪是海洋的世纪,随着能源供应的短缺日益严重,世界各国正逐渐将目光转向物资丰富的海洋。珊瑚礁作为人类在海洋开发中天然的平台,有着重要的战略发展价值。近年来,国内外已经出现了一些在珊瑚礁建造人工岛、防波堤等建筑物。波浪在珊瑚礁礁坪破碎、传播后到达防波堤,产生爬高,波浪爬高是决定防波堤高程、人工岛高程的重要因素。研究波浪在岛礁地形下的传播变形、破碎和在防波堤爬高等水动力学特征,对于实际工程建设和岛礁保护有重要意义。
近年来,国内外学者对珊瑚礁地形上的波浪变形已经有了部分的研究工作。Michael R.Gourlay[1]采用明渠流理论,分析关系推导礁坪处波生流的条件,礁坪水深的物理特性,并做了相应了物理模型试验。Pablo D Quiroga[2]利用物理模型试验探讨了孤立波传播过岸礁地形时的演变规律,探讨了物理模型试验中底摩擦对波浪传播的影响。柳淑学[3]对波浪在珊瑚礁地形上的传播特性进行了物理试验研究,将珊瑚礁地形简化为坡度为1:5的陡坡加较长水平礁坪段的地形,对规则波和不规则波在该地形条件下的波浪破碎及波高沿程衰减进行了研究。姚宇通过波浪水槽试验对珊瑚礁破碎带附近波浪演变规律开展研究,采用概化的岸礁模型,测试水深分别为0.38 m、0.4 m、0.42 m、0.45 m,礁前斜坡坡度分别为1:3、1:6、1:9、1:12和入射波高从0.01~0.13 m的组合工况[4],礁冠宽度为0.025 m、0.1 m、0.2 m、0.4 m、0.8 m以及无礁冠模型[5],对破碎带宽度和破碎带附近波浪的入射、反射、透射以及能量耗散进行了测量分析。张善举[6]建立了适合陡峭珊瑚礁地形的 Boussinesq 型波浪数值模型,提出波浪混合破碎模型的改进方法,提高了计算精度,同时建立了具有层状骨架或树枝状骨架的珊瑚体礁面上波浪传播数学模型。
当变形后的波浪传播到了护岸或防波堤时,便会在防波堤上爬高,波浪的最大爬高值对防波堤的设计有重要影响,因此,如何确定最大爬高值以及如何减少波浪的最大爬高值,一直是防波堤研究的重要课题。龚崇准[7]进行了波浪在具有糙插砌条护面的斜坡堤上爬高的实验,通过理论和试验结果分析,提出了计算加糙斜坡堤波浪爬高的计算公式。林文婧(2015)[8]结合具体工程实例,探讨了混合式海堤波浪爬高的计算公式。黄元中(2017)[9]使用边界条件法造波,波浪阻尼算法的海绵层模型进行消波,建立三维数值波浪水槽,构建异型预制块斜坡堤,数值模拟线性波与非线性波下异型预制块护坡波浪爬高过程。
波浪在珊瑚礁礁坪破碎、强非线性传播后到达防波堤,珊瑚礁破碎后的波浪在防波堤的爬高与前述非破碎波的爬高情况不同,以往公开发表的论文鲜见开展珊瑚礁礁坪上所建防波堤的波浪爬高数值模拟试验。本文基于FLOW-3D软件建立了珊瑚礁地形下防波堤波浪爬高的数值模型。通过与物理模型对比,对珊瑚礁地形上波浪传播、破碎、非破碎波浪的防波堤爬高进行了验证。在此基础上模拟了波浪在珊瑚礁地形上破碎与传播、防波堤的爬高,分析了防波堤位于不同位置时波浪爬高的变化。
2 数学模型
2.1 控制方程
控制方程选取Navier-Sotkes方程。
在处理不可压缩流体问题时,连续性方程为:
(1)
动量方程为:
(2)
式中u、v、w分别是x、y、z方向上的速度分量;Ax、Ay、Az分别代表x、y、z方向上具有流动性的面积分数;VF是体积分数;ρ是流体密度;p是压强;t为时间;Gx、Gy、Gz分别是x、y、z方向上的重力加速度;fx、fy、fz分别为x、y、z方向上的粘性力。
2.2 边界条件
入口边界:FLOW-3D入口边界造波条件(Wave)是在网格边界上基于线性波理论、Stokes五阶波理论、孤立波理论和不规则波理论进行造波,根据所需要的波要素计算相应的厄塞尔数,然后根据厄塞尔数决定采用何种理论进行造波,就能模拟出相应的波浪。
出流边界:需要一种边界条件让水槽中模拟的波浪平稳流出计算网格,并将反射减小到最小,在FLOW-3D中选择自由出流边界(Outflow)。
自由液面:由于选择的流体是20℃的水,是单体流体,有自由表面边界条件,故空气对流体的作用表现在流体的表面受到大气压力,即pa=p(大气压力),在FLOW-3D中选择(Specified pressure),并设置相对大气压为0。
其他边界:垂直流向方向上设置对称边界(Symmetry),即在边界上没有流量通量和剪应力,在二维和三维模型里都可以设置成这个条件。
zmin是水槽底部,为了模拟真实情况下波浪的下部条件,设置成Wall。
3 数值模型
3.1 造波验证
采用波高为0.02 m,周期为1.25 s的试验波,厄塞尔数U=0.99;水槽为原水槽,分别在X=0 m,5 m,10 m,15 m处设置测点,选取稳定波形与理论解进行对比,stokes二阶波面方程为:
(3)
式中H为波高;k为波数;σ为角频率;t为时间;L为波长。
不同位置处波面数值解和理论解比较如图1所示。
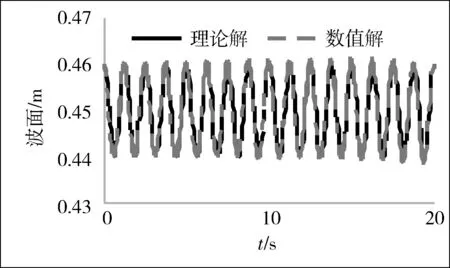
(a) X=0处波面数值解和理论解对比

(b) X=10处波面数值解和理论解对比
3.2 破碎验证
根据长沙理工大学姚宇[5]物理模型的实验条件,实验设置如下:
试验在长为36 m,宽为0.55 m,高为0.6 m的波浪水槽中进行,一端装有造波机,另一端有多孔材料的消波层,礁前斜坡的坡度m=3,入射波高为h=0.095 m,水深H=0.45 m,周期为1.25 s。
数值模型设置:数值模型为简化了的物模模型,采用单宽的二维模型模拟,数值水槽长为36 m,宽为0.01 m,高为0.6 m,波高、周期、水深均和物模相同,斜坡的位置和坡度也和物模相同,水槽末端设有长为6 m的消波体。物模实验简化后模型如图2所示。

图2 姚宇物模实验简化后模型示意
数值试验的网格长宽均为0.01 m,具体划分如图3所示。
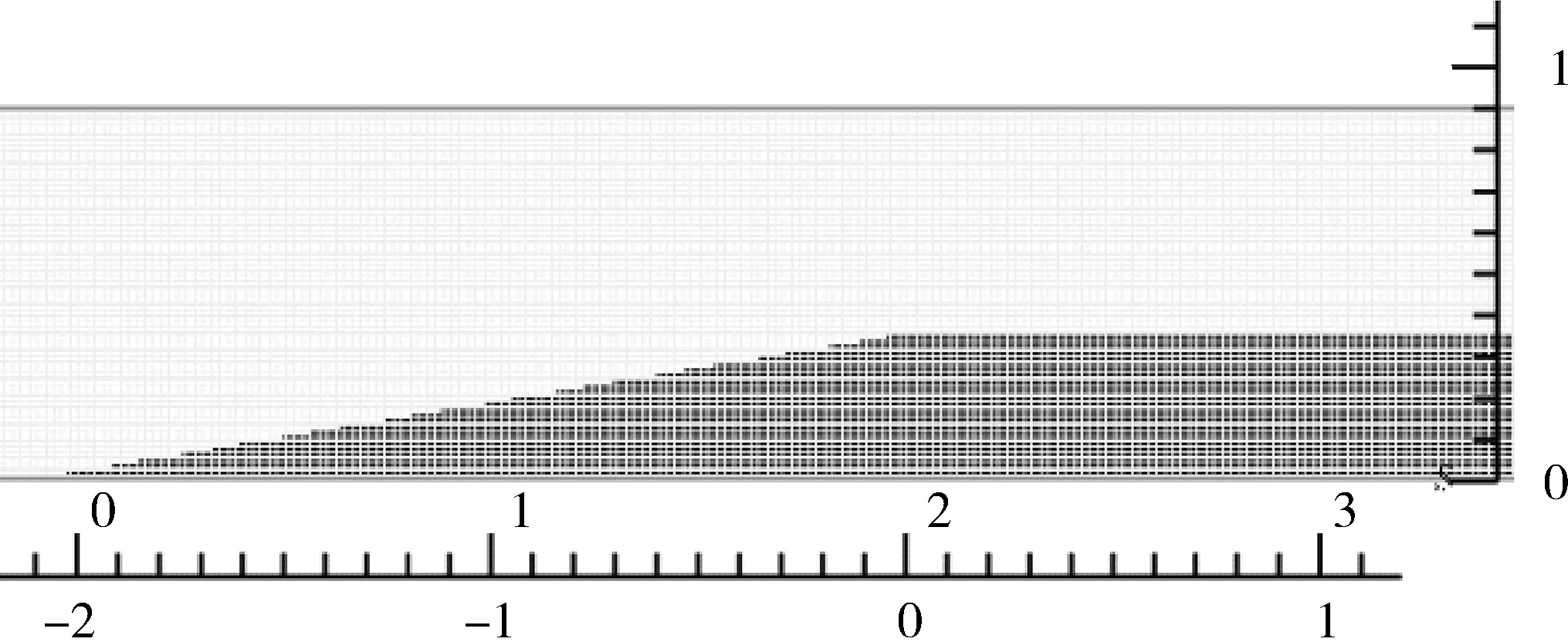
图3 礁缘附近网格划分示意(单位:m)
计算了从-8~10 m处各点的稳定后波高,并与姚宇实验测量值进行对比。
从图4中可以看出,模型对波高的模拟和实验值吻合较好,礁坪前存在驻波,体现了斜坡对波浪的反射作用,破碎位置位于礁缘附近,破碎后波高急剧减小,本实验很好的模拟了破碎过程。
3.3 爬高验证
由于前述姚宇[5]物理模型未进行波浪的防波堤爬高实验,这里采用龚崇准[8]物理模型的实验结果对数值模拟进行验证。实验设置如下:

图4 数值试验中波高和实测值的对比示意
试验在长为32 m,宽为0.5 m,高为0.7 m的波浪水槽中进行,一端装有造波机。斜坡堤面选择糙率kp为0,坡度m=3。造波机的波高为h=0.08 m,水深H=0.32 m,波长L分别取1.2 m、1.6 m、2.0 m,该条件下波浪在水槽中未破碎。
数值模型设置:数值模型为简化了的物模模型,采用单宽的二维模型模拟,数值水槽长为32 m,宽为0.01 m,高为0.7 m,波高、波长、水深均和物模相同。
通过对数值模型的分析计算,可对波浪在光面护坡上的爬高过程进行模拟(如图5所示)。在水面位置时,水质点运动方向与行进波方向相同,水质点受来波波能影垧,沿护坡坡面开始爬坡;当来波波能与爬坡消耗的能量达到平衡时,波浪的爬高达到最大,在最高位置时,水质点方向呈竖直或与沿重力分量及摩摞力方向一致;之后水质点沿坡面回落,直至下一倒波到达,此时为爬高过程中的最低位置,水质点运动方向较为混乱。

t=19.3

t=19.9

t=20.5
在得到完整的计算数据后,分析计算时间内波浪在X方向沿斜坡堤护面上爬高的数值得到最大爬高的时间段,再将该时间段内提取相应截面的自由液面高度,最终得到最大爬高值,得到模型数据与试验数据对比见表1。
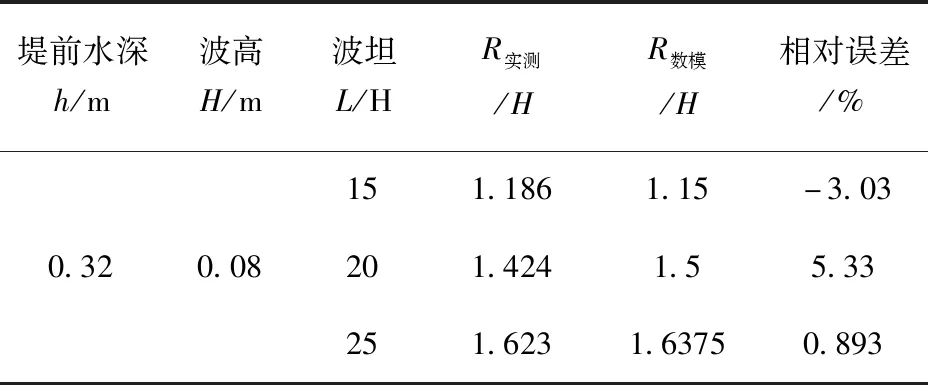
表1 波浪爬高实测数据与模拟数据
比较表明,相对误差最大为5.33%,平均误差绝对值为3.08%,数值模拟的波浪爬高数值与物理实验结果较为接近,说明在本文所创建的数值波浪水槽中,波浪在斜坡堤上爬高具有较高精度,证明该数值水槽具备分析这类问题的可靠性。
4 珊瑚礁地形下防波堤波浪爬高的数值模拟与基本特点分析
根据前文的试验结果,开展珊瑚礁地形下防波堤波浪爬高数值试验,模拟防波堤离礁缘不同距离对波浪爬高的影响。
试验由姚宇的波浪破碎验证试验改进得来,由于部分工况下波浪爬高的高度超过了原水槽的最大高度0.6 m,于是将原水槽的高度加高为0.9 m,y方向网格数加大为90(如图6所示)。加入一个可调整水平位置,坡度为1:2的斜坡防波堤,通过几组不同工况下波浪爬高值的计算,分析不同位置的防波堤对爬高值的影响(见表2)。
对于4种不同工况,防波堤分别置于礁坪上不同位置,统计不同位置防波堤的最大爬高值(如图7所示)。
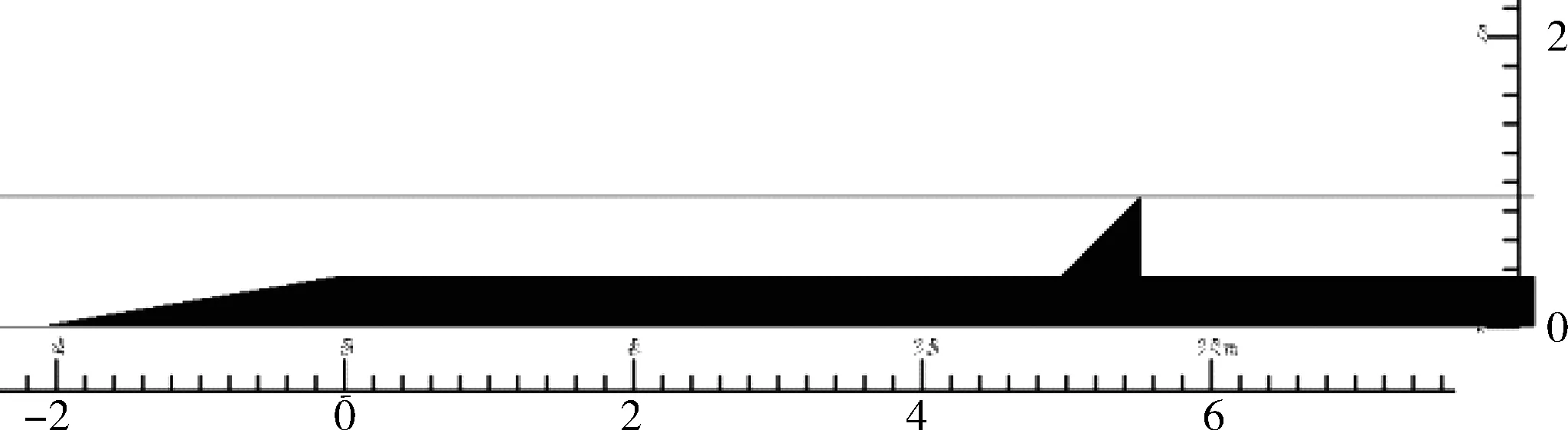
图6 波浪爬高试验示意(单位:m)

表2 不同工况下波要素
结果表明:当初始波高较小时(小于0.03 m),波浪在防波堤上的爬高值与防波堤位置基本无关;当初始波高达到一定大小(0.06 m),即波浪开始发生明显破碎时,最大爬高值随着防波堤离礁趾距离的增大而减小。水深越大的工况,相同波高所能达到的最大爬高值越大,说明当水深较小时,波浪在传播到礁前之前已经发生部分变形,导致能量损耗。
在离礁前缘距离较近的防波堤,波浪爬高很大。随着礁坪上防波堤离礁前缘距离的增大,波浪爬高先明显下降,之后趋于稳定,在距礁前缘约一个深水波长处的防波堤爬高已显著减小。结合波浪破碎的沿程变化,当距礁前缘约0.4个深水波长处(坐标3.5 m),波浪已经破碎完全,破碎后波高的沿程变化不大,但波浪爬高值的沿程显著变小,因此,波浪爬高不仅与防波堤所在位置处破碎波高和初始水深有关,还与波浪破碎阶段有关。

(a)工况1
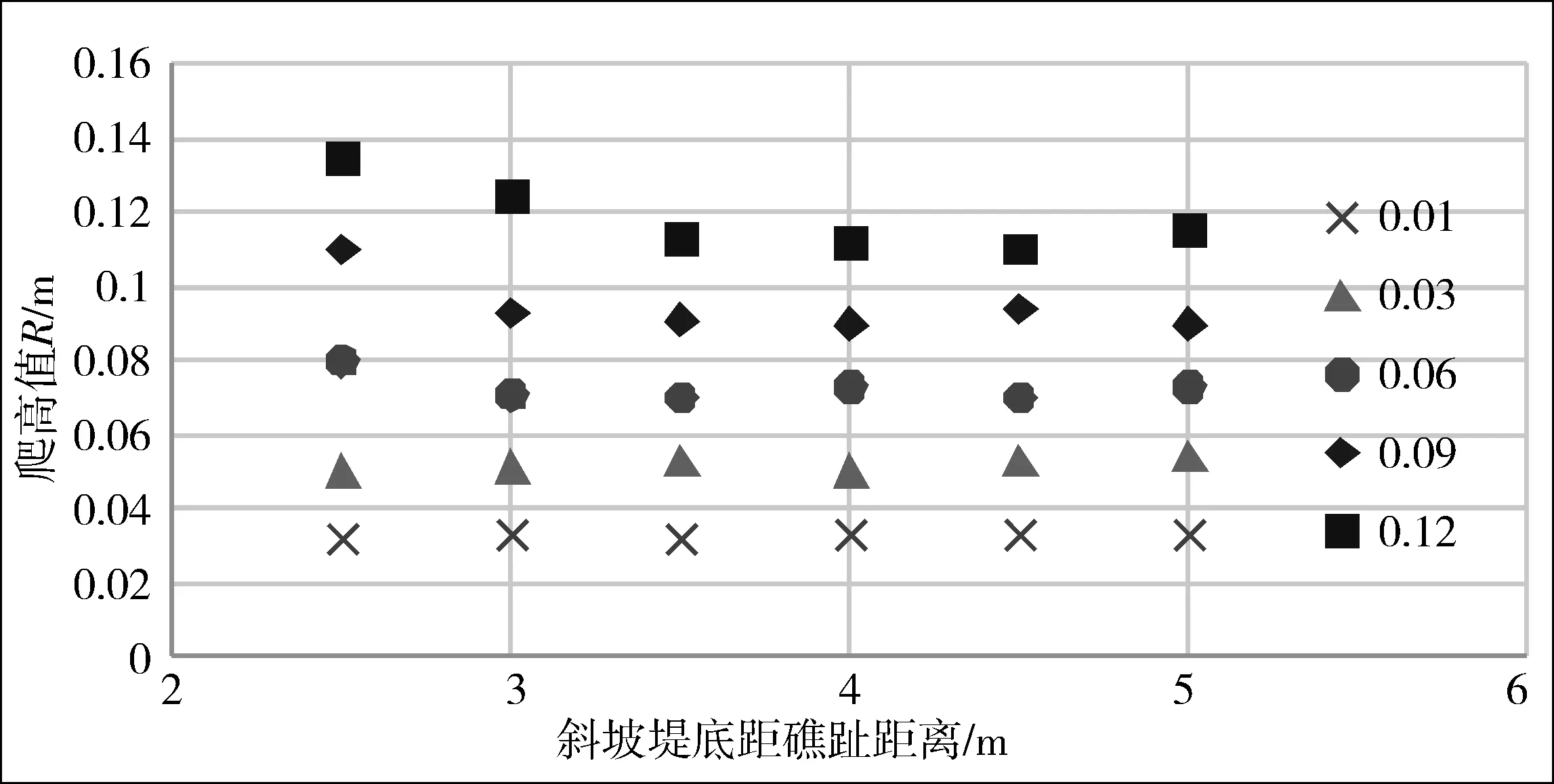
(b)工况2
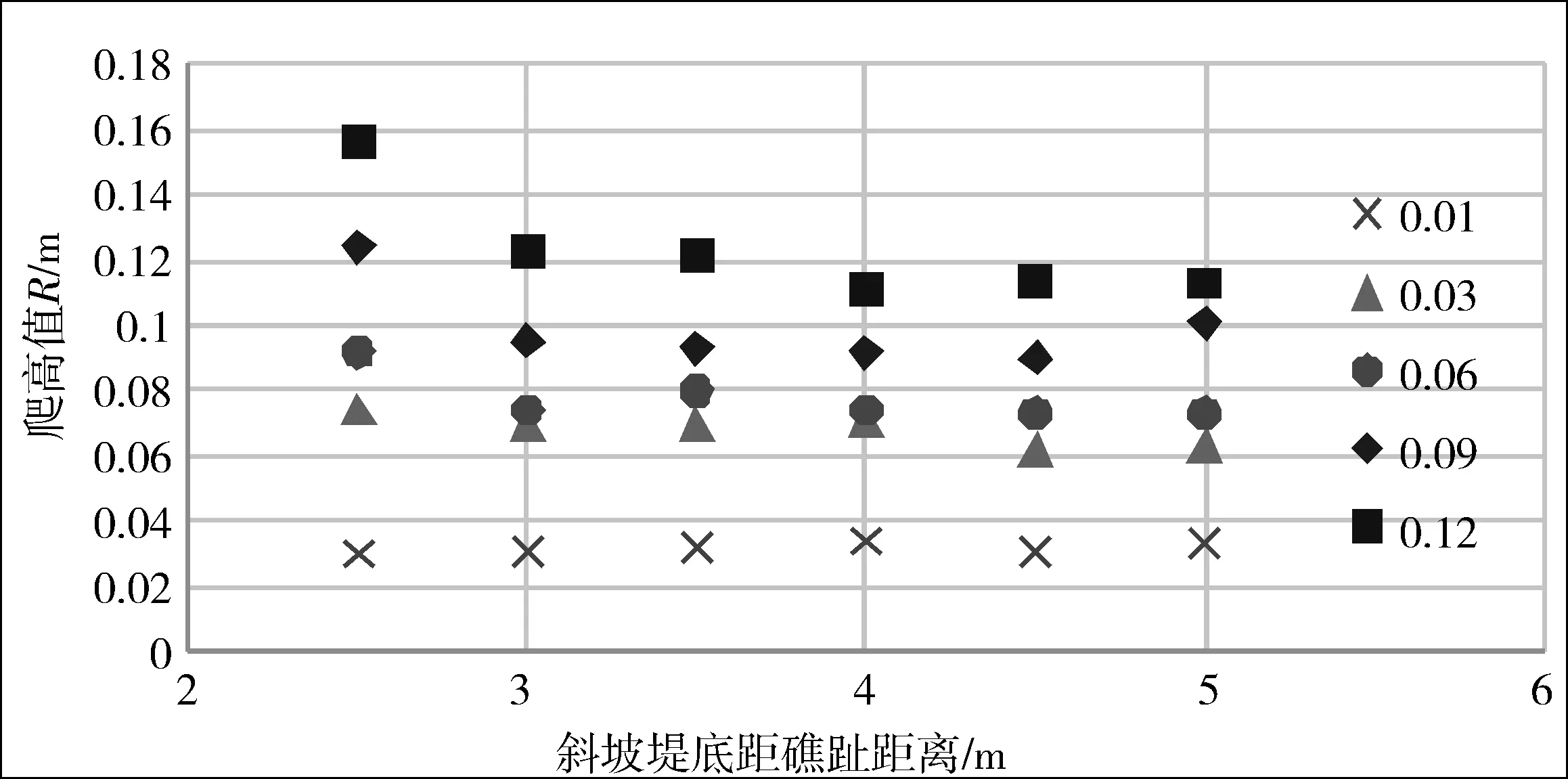
(c)工况3
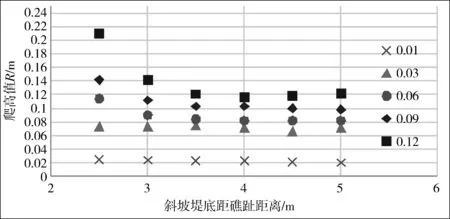
(d)工况4
5 结语
1) 本文基于FLOW-3D软件,建立了珊瑚礁地形下防波堤波浪爬高的数值模型。
2) 在离礁前缘距离较近的防波堤,波浪爬高很大;随着礁坪上防波堤离礁前缘距离的增大,波浪爬高先明显下降,之后趋于稳定,在距礁前缘约一个深水波长处的防波堤爬高已显著减小。波浪爬高不仅与防波堤所在位置处破碎波高和初始水深有关,还与波浪破碎阶段有关,在距礁前缘约一个深水波长处的防波堤爬高已显著减小。
3) 在有限水深的条件下,防波堤的合理布置可以有效减少非线性波在珊瑚礁上防波堤的爬高值,而在深水条件下作用很小。

