基于液固两相流排污管道冲蚀磨损的数值模拟

许爱荣，冯昌兴

（西安石油大学机械工程学院，陕西 西安 710065）

冲蚀磨损是一种普遍的磨损破坏形式，它是指固体表面材料与含有固体颗粒的流体相接触并发生相对运动时所导致固体材料损耗的现象。冲蚀磨损根据流体介质的不同又可以细分为液固冲蚀磨损和气固冲蚀磨损两大类[1]。液固两相流对材料的冲蚀在石油、化工等领域广泛存在。

近年来，基于CFD的磨损研究得到了国内外学者的关注。陈宇等[2]人采用DPM冲蚀预测模型，模拟分析油品中夹带的固体颗粒对三通管的冲蚀磨损情况，得出固体颗粒对三通管冲蚀的分布规律；金浩哲等[3]人以液固两相流冲洗油管道为研究对象,采用Realizable κ-ε湍流模型、随机轨道模型，结合液固两相流冲蚀磨损试验,建立修正的冲蚀磨损数理模型，数值预测典型工况下冲洗油管道内速度、压力、冲蚀磨损率等流动参数分布情况；王凯等[4]人以弯管为研究对象，预测出颗粒对弯管壁面的冲蚀破坏情况。

目前大量的研究工作都是围绕弯管进行分析，对T型管道的研究较少。针对这一现状，本文以排污管道为研究对象，以期深入了解冲蚀磨损的影响规律。

1 计算模型

1.1 湍流模型

流体流动模型选用标准的k-e方程，标准k-e模型是一种经验模型，基于湍流能量方程和扩散速率方程。它是基于Wilcox k-e模型，考虑了低雷诺数、可压缩性和剪切流传播，因此可应用于墙壁束缚流动和自由剪切流动。

标准k-e模型的湍流动能和湍流耗散的输送方程[5]如下所示：

方程中Gk为层流速度梯度而产生的湍流动能，Gb为浮力产生的湍流能项，YM为在可压缩流动中湍流脉动膨胀到全局流程中对耗散率的贡献项，C2ε、C3ε是经验常数，σk和 σε为 k 方程和 ε 方程的湍流Prandtl数，Sk和Sε为用户定义的湍流能项和湍流耗散源项。

1.2 离散相控制模型 [6]

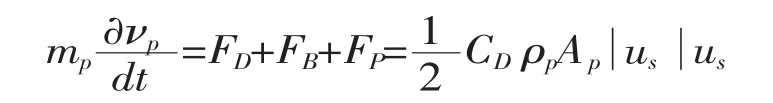
式中，mp为质量流量，kg；A为颗粒与壁面发生碰撞的面积，m2；FD为拽力，N；FB为浮力，N；Fp为压力梯度力，N；mF为颗粒流过计算域的质量，kg；CD为颗粒与液相见拽力系数，无因次；ρp为颗粒密度，kg/m3；us为流体流速，m/s；dp为颗粒直径，m；p为压力，N；νp为颗粒冲击速度，m/s；g为重力加速度，m/s2。

1.3 固体颗粒冲蚀磨损模型

基于前人的理论研究，本文选用fluent中的DPM模型为连续油管的冲蚀模型。冲蚀率公式[7]为：

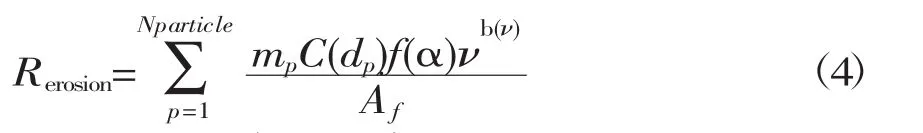
式中，Rerosion为冲蚀速率，kg/(m2·s)；mp为颗粒质量流量，kg/s；C(dp)为颗粒直径参数；f(α)为冲角角度函数，f=1；ν为颗粒的碰撞速度，m/s；b（v）为速度分量函数；Af为碰撞壁面的面积，m2。

2 T型管道有限元模型

2.1 几何模型及其网格

Fluent是目前相对成熟且使用广泛的商用流体分析软件。本次二维模型使用SolidWorks进行建模，导入到Fluent进行网格划分，如图1所示。管道操作条件为常温常压，y向的重力加速度为-9.8m/s2。

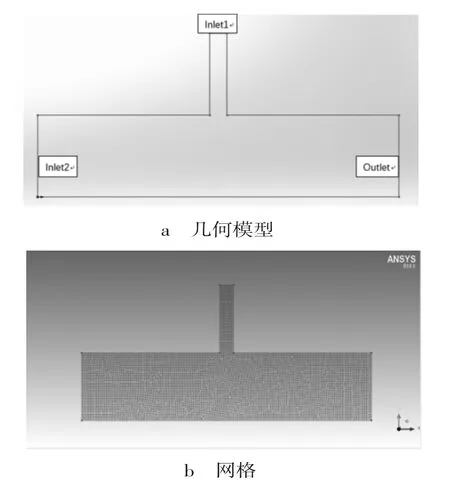
图1 排污管道几何模型及网格

2.2 离散相模型设置

Fluent中的DPM模型把流体视为连续相，流体相为牛顿流体，把固体颗粒视为离散相。开启Erosion/Accretion模型，喷射类型为表面，选择inlet1为喷射入口，沙子速度为0.1m/s，直径为0.00001m，开始时间为0，结束时间为50s，质量流量为0.1kg/s，

2.3 边界条件

边界条件包括inlet1，inlet2，outlet，wall四个方面，见表1。同时为了便于模拟，假设固体颗粒为质量密度均匀的球形，离散相颗粒进行无旋转运动。

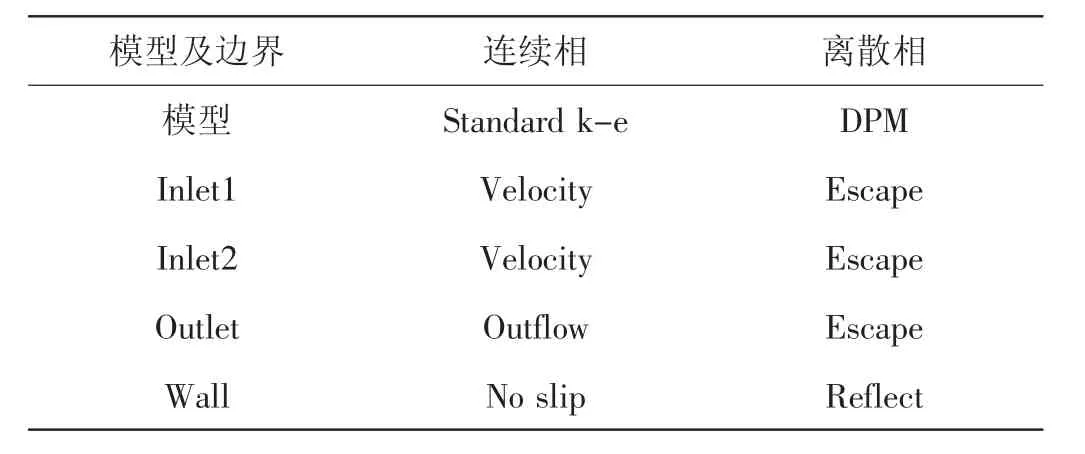
表1 边界条件设定

设置入口1出的液体速度为10m/s，湍流强度为1%，入口2处的液体流速为0.1m/s，湍流强度为1%。选取SIMPLE求解器，计算入口设为inlet1，完成初始化。设置时间步长为0.05s，迭代次数为1000步，进行求解。

3 数值模拟结果分析

在两相流的耦合计算中，先计算得到收敛或部分收敛的连续相流场，然后创建喷射源，在计算域中引入离散相进行耦合运算，分别得到压力，速度和冲蚀云图，进行分析。

3.1 压力云图分析

由图2可知，随着入口一（分支管）液体的流入，最大压力位置由出口（总管）的末端转移到分支管与总管下底面连接偏右的位置，最终，两者基本一致；总管左端受分支管的影响压力先增大后稳定，总管右端基本保持不变。

图2 压强分布云图

3.2 速度云图分析

由图3可知，速度分布云图正好和压力相反，速度大的位置压力小，符合流体运动规律。

3.3 冲蚀云图分析

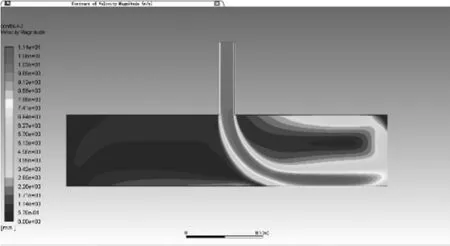
图3 速度云图

由图4可知，冲蚀发生的主要位置位于分支管与总管的交界处的右端，其他部分的冲蚀磨损较小。

图4 冲蚀云图

4 结论

1）基于排污管道的CFD冲蚀计算模型计算结果符合实际情况，验证了模型的准确性。

2）对于排污管道而言，分支管与总管的交接处是发生冲蚀磨损最严重的位置，需要加强此处材料的强度，涂抹保护层等措施来提高抗冲蚀效果。