一种利用形态相似性的水稻信息提取算法

高永康，王腊红，陈家赢，李建民

(华中农业大学 资源与环境学院，武汉 430070)

0 引言

中国65%人口的主食为稻米，2013年中国稻米产量已占世界稻米产量的28%。及时、有效地获取水稻分布信息，对优化粮食生产布局、指导粮食生产，保障国家粮食安全具有重要意义[1]。

针对水稻种植分布的调查，传统方法如农业报表和实地抽样法，工作量大，成本高，时间跨度大，不能及时有效地获取水稻种植信息以指导粮食生产。而由于遥感技术快速发展，通过遥感手段来快速、方便地获取地面目标区域大范围覆盖数据，实现地表覆被的识别已成为大范围作物监测的重要手段[2-5]。其中，归一化植被指数(normalized vegetation index，NDVI)作为一种植被监测领域的重要指标，在作物识别、农作物产量估测、植被覆盖动态监测等方面[6-10]均有着广泛的应用。

利用作物的NDVI时序数据来提取作物空间分布，最直接的方式即判断未知像元点NDVI时序曲线与目标作物标准NDVI时序曲线间的相似性，选择恰当的阈值来判断该未知点是否属于目标作物类别。时间序列由于自身具有形态多变性，容易出现振幅平移、伸缩、线性漂移及时间轴伸缩和弯曲等形变[11]，使得在保证效率及准确性的基础上对时间序列的相似性度量尤为困难。特别地，对于通过遥感手段，基于地表覆被时序数据来识别作物类别来说，由于受到天气影响较大及作物物候空间分布差异，更增添了时序曲线的突变性。

为了提高NDVI时序数据的质量，陆俊等[12]利用时空数据融合算法(spatiotemporal data fusion algorithms，STDFA)，获取了兼具Landsat-8 OLI影像空间分辨率和MODIS 8 d地表反射率合成产品(MOD09Q1)时间分辨率的融合影像。基于该数据，使用支持向量机(support vector machine，SVM)方法得到的水稻制图精度达到94%，效果较好，但算法实现较为复杂，融合以小窗形式逐步进行，计算资源消耗较大。郭昱杉等[13]基于欧式距离方法对冬小麦、玉米和棉花3种作物进行空间信息提取，总体制图精度达到86.90%，但由于欧氏距离对时间序列的突变和噪声较为敏感[14]，适用性较差，如玉米的制图精度仅有79%。一般地，对欧氏距离的使用应基于相应的转化，以降低其对突变和噪声的敏感性。如动态时间弯曲距离(dynamic time warping distance，DTW)，其通过基于累积距离矩阵的动态规划方法，求解序列之间的动态时间弯曲距离[15-16]，已有研究表明动态时间弯曲距离方法在提取地表覆被信息方面具有较好的适用性。韩晓勇等[17]使用DTW方法对秦巴山区水田、旱地等植被信息进行提取，总体制图精度为83.80%。管续栋等[18]基于DTW方法对泰国东北部进行水稻的提取，其制图精度为83.38%。但DTW算法复杂度较高，在等长序列比较中，相对于SVM、欧式距离等方法并没有明显的优势，使其的使用受到限制[17-19]。

为找寻一种既容易实现，又具有较高的地物提取精度的方法，本研究基于欧式距离，考虑曲线的形态分布特征，提出了一种根据对应元素特征距离大小，对特征间距离进行差异性放大的算法，以此对水稻信息进行提取，并验证算法的有效性。

1 研究区域

仙桃市位于湖北省中部，地处江汉平原，在112°55′E～13°49′E、30°04′N～30°32′N之间。市境内地形大部为冲击平原，地势平坦；气候属于亚热带季风性气候，常年气候温和，雨量充沛，日照充足，年平均日照时数在2 000 h以上，无霜期一般256 d，是传统的农业区。仙桃市总面积2 538 km2，2017年全市耕地面积900 km2，占比35.5%，其中水田580 km2，旱地323 km2，粮食作物以小麦、水稻为主，经济作物以棉花、油菜为主。

2 数据与方法

2.1 MODIS数据及其预处理

本研究所用遥感数据是从NASA官网(https：//reverb.echo.nasa.gov/reverb/)获取的2005—2015年仙桃地区MOD13Q1数据。图幅行列号为h27v05，一年计23幅图像，11年共计253幅。该数据已做过辐射校正、几何校正等基本处理。MOD13Q1数据集包含NDVI图层、EVI图层、红光波段、近红外波段反射率等数据，它们的时间分辨率均为16 d，空间分辨率为250 m。

作为一种高时间分辨率的植被监测数据，MODIS NDVI数据有助于实现植被季节间及年际变化比较，研究表明，NDVI对植被的生长变化较为敏感[20-22]。MODIS NDVI数据本身已经过处理，极大降低了噪声的存在，但时序噪声仍然不可避免，因此考虑到噪声的影响，本文对MODIS NDVI数据进行经验模态分解处理，去除小尺度噪声，重新构造时间序列，其分解过程如图1所示。图1中，IMF1～IMF3分别为第1～3次模态分解分量,res表示模态分解最后所得的趋势项。根据经验模态分解原理，IMF(intrinsic mode function)分量越靠前，其体现的变化越细微，时间尺度越小；但由于尺度越小，观测信号受到噪声影响越大，因此IMF分量信噪比越低。据对样本数据点的抽样观测，发现基本分解到2～3次即停止分解，而且第一个IMF分量多成锯齿状，信噪比过低，噪声影响过大，难以发现其变化规律，而其余分量则趋势性比较明显(图1)。因此，本文决定舍弃第一个IMF分量，根据剩余分量和趋势项重建NDVI时序数据。

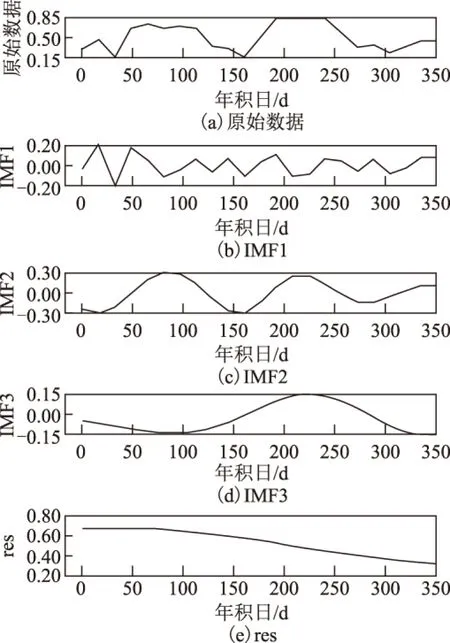
图1 经验模态分解示意图

2.2 统计数据及样本获取

小麦、油菜、中稻等作物物候信息(表1)来自中国农业部种植业管理司分省农时数据库(http：//202.127.42.157/moazzys/nongshi.aspx)。江汉平原耕作制度基本为一年两季，主要以2种种植模式为主：其一为小麦/油菜-中稻/棉花模式(中稻种植面积远大于棉花，以下简称单季稻模式)；其二为早稻-晚稻模式(以下简称双季稻模式)。

由于植被生长周期的存在，植被对红光波段的吸收利用同样具有周期性，而近红外波段比较稳定，光合作用越强，红光吸收率越高，反射率越低，NDVI值也就越高。不同植被物候期有差异，因此光合作用最强的时期也就不同，表现在NDVI时序曲线上，即是波峰所处时期有所不同。

另一方面，对于非植被来说，近红外波段与红光波段吸收率季节性变化不大，波动较小，故非植被反射率在时间上较为稳定，且与光照强度成正相关，表现在NDVI时序曲线上，波动较植被明显更为平缓，NDVI值随季节更迭做小幅波动。这些特性使得基于NDVI时序曲线对地表覆被进行信息的提取成为可能。

由表1 可以看到，单季稻模式中，在第一季作物中，小麦的抽穗期出现在3月下旬至4月中旬，油菜的开花期处于3月上旬至4月中旬，此时生长状态最为旺盛，NDVI值会达到最大；在第二季作物中，中稻在6月上旬至7月下旬之间处于抽穗期，棉花6月下旬至8月中旬处于开花期，在此阶段，二者NDVI值会达到峰值。对于双季稻模式，从表1中可以看到，早稻会在4月下旬开始移栽，6月中旬至6月下旬左右开始抽穗，晚稻则在9月中旬至9月下旬开始抽穗，NDVI在此时期出现波峰。

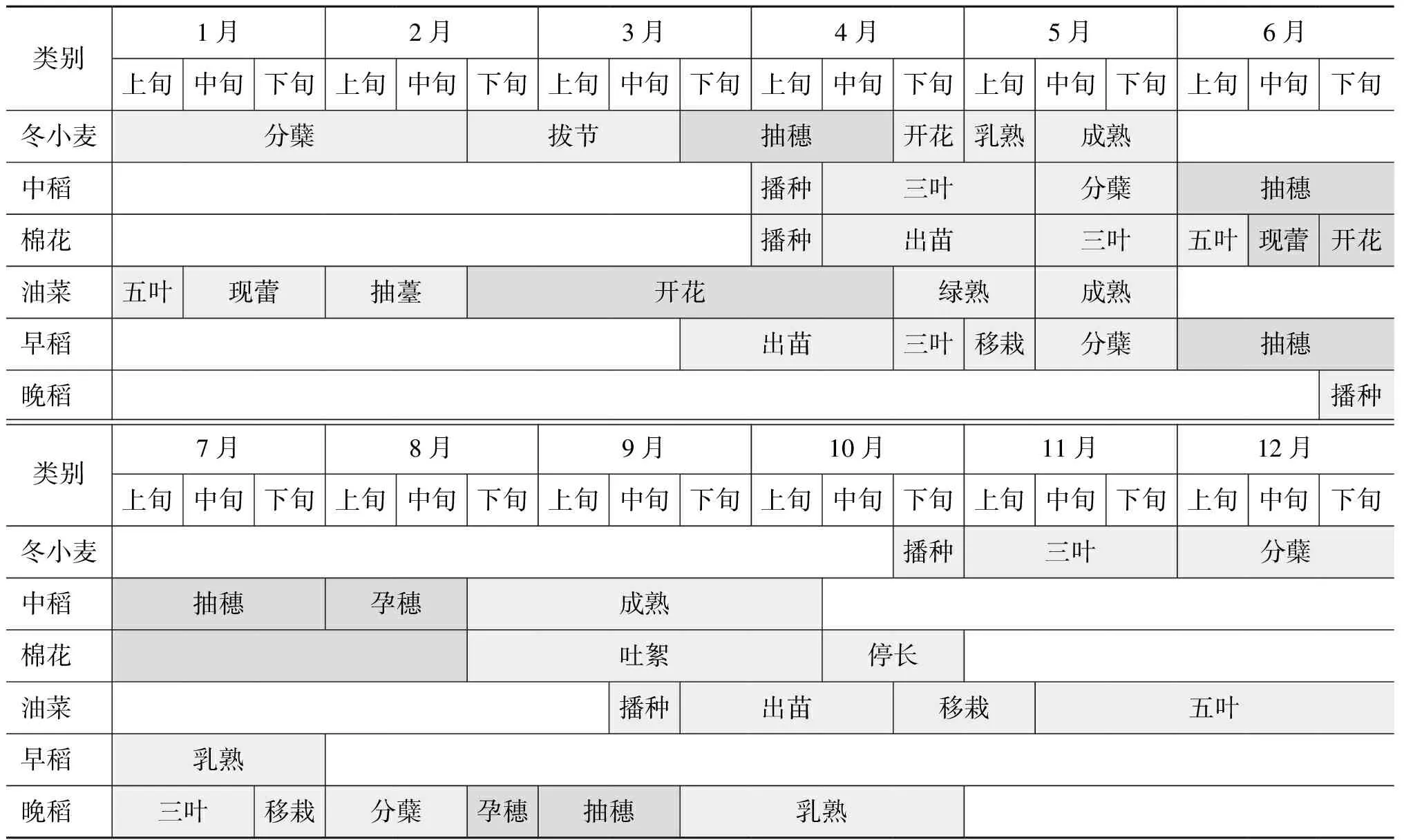
表1 一年中各类型作物生长物候期分布

注：颜色深浅代表该种作物覆盖度高低；无色表示该时期未种植该作物。

为了对文中所提形态相似性测量算法进行有效性检验，本文共提取了5种地物样本数据，其中根据上述分析，由于单季稻和双季稻具有明显的独特双波峰特征，因此利用该物候特征对单季稻和双季稻进行样本数据的初步提取，具体筛选条件如表2和表3所示。之后，对初步提取样本进行相关性分析，选择样本彼此间相关性大于0.9的样本作为最终样本。

表2 单季稻NDVI时序曲线特征

表3 双季稻NDVI时序曲线特征

同时，由于研究区面积较小，为了避免采样出现极端情况，即样本的分布过于偏离正常区间，表4中所有样本的获取均是在湖北省尺度上进行。虽然表1中所列作物物候每年将会有所不同，但由于本研究所使用NDVI数据时间分辨率为16 d，物候的年际变动幅度将不足以对样本的提取产生较大的影响。

表4 用于算法检验的各地表覆被类型样本数目 个

注：以上均为11 a总体样本。

在天地图的帮助下，目视选取城镇用地、水域、森林3种地表覆被类型样本参与算法的检验，其中每个样本选取区域面积基本大于4 km2，均大于1 km2。因为存在研究区11 a的NDVI数据，故为了丰富样本总量，以减少异常数据的产生，每个样点位置均重复采集11次，各类型样本数目如表4所示。为了方便算法的有效性测试，表中各类样本均是在省级水平上采样，并经过筛选得到的最佳样本。

仙桃市水稻种植主要为中稻，双季稻种植面积少且分散，使用MODIS NDVI数据提取双季稻结果客观上可能精度不够理想。因此在检验算法对实际情况的适应性时，仅提取中稻，即单季稻空间分布信息，提取时根据表2所示条件，在仙桃市范围内对单季稻样本进行再次取样，结果如表5所示。

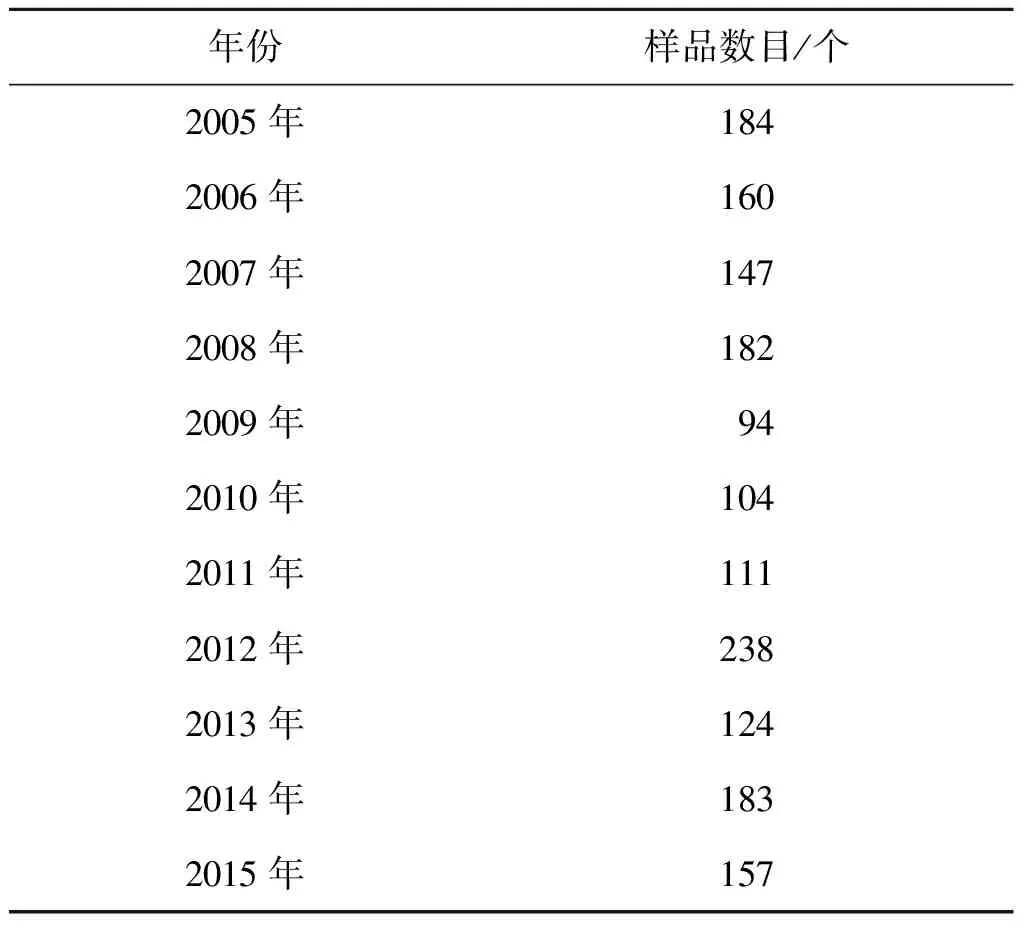
表5 2005—2015年仙桃市单季稻样本数目

2.3 形态相似性度量算法(morphological similarity measurement algorithm，MSMA)

本研究通过NDVI时间序列之间相似性的计算，并基于合理的阈值划分，获取研究区水稻种植空间分布信息。为了计算NDVI时序曲线之间的相似性，首先需要获取水稻标准时间序列，其为对样本数据集对应元素取平均得到，见式(1)。

Sst(i)=mean(Sset(i))，i∈(1，2，3，…，n)

(1)

式中：Sst(i)表示水稻NDVI标准时序数据的第i个元素；Sset(i)表示样本NDVI时序数据集的第i个元素集合；n为时间序列长度；mean表示取平均函数。

考虑到空间位置导致的异常值的影响，在计算标准时序曲线之前，首先通过阈值法剔除异常值，上下限阈值的确定如式(2)～式(3)所示。

up_thd(i)=pri_75(i)+1.5×pri_75_25(i)

(2)

low_thd(i)=pri_25(i)-1.5×pri_75_25(i)

(3)

s.t.i∈(1，2，3，…，n)

式中：up_thd(i)、low_thd(i)分别表示样本数据集中第i个元素集合阈值上限、阈值下限；pri_25(i)、pri_75(i)、pri_75_25(i)则分别为样本数据集中第i个元素集合的25%分位数、75%分位数，及二者之差绝对值。修正后的标准时序曲线获取函数如式(4)所示。

(4)

为确定未知像元时间序列在各个时间点相对于标准时间序列的变化幅度，计算出样本数据集各个特征元素与标准时间序列的对应元素平均绝对值距离Dmean(i)作为参考，称之为特征均距，如式(5)所示。

(5)

式中：abs表示对元素取绝对值。

对于给定未知像元NDVI时间序列，S1=(k1，k2，k3…，kn)，及标准像元NDVI时间序列S2=(l1，l2，l3…，ln)，考虑到曲线的形态特征分布对相似性的影响，本算法不对整个时间序列计算欧式距离，而是针对2个时间序列对应元素之间计算欧氏距离Deuclid(i)，见式(6)。

(6)

于是，可得未知像元与标准像元的各个特征元素距离与相应平均距离之差，称之为特征偏移距离，偏移距离最小为-Dmean(i)，此时认为未知像元第i个特征与标准像元第i个特征完全相同，如式(7)所示。

Drel(i)=Deuclid(i)-Dmean(i)

(7)

最终形态相似性距离计算形式如(8)式所示，其中α为偏移距放大项。当α为1时，形态相似性距离等同于绝对值距离，因此为了保持算法的稳定性，α取值应大于等于1。

(8)

为了尽量减少外界干扰误差，偏移距放大项α应根据数据本身生成。考虑到偏移距本身大小即是特征相似性的重要度量，简单地以线性方式对偏移距进行放大，单位偏移距放大效果相同，缺乏对偏移距本身大小的重要性的突出考虑，因此对于α项，应考虑非线性方式放大。本文取指数函数作为放大基本式，如式(9)所示。

(9)

式中：对各特征元素特征偏移距与特征均距做除法，结果即为偏移距相较于特征均距的倍数，即偏移倍数，取偏移倍数作为基础指数。对基础指数，即偏移倍数加1以确保α项取值范围为大于等于1的实数。由于α项的确定仅依赖于数据本身，因此无人为及其他因素干扰。

综上所述，本研究中形态相似性度量距离计算如式(10)所示。

(10)

其中，为了增强算法的适应性，防止过度地对偏移距进行放大，算法中添加β为偏移倍数调整因子。β越大，偏移放大效应越明显；当β为0时，该算法等同于绝对值距离。由于噪声的存在，适宜的β值应是使算法在有着恰当的噪声放大效果的同时，可以最大化地物时序曲线类别的差异。

2.4 阈值选择与精度控制

针对使用相似性度量来提取地物类别的方法，阈值选取对精度至关重要。关于阈值的选取，存在标准差法、分位数法、试凑法等。对于标准差法，一般选择标准样本曲线加减2倍或3倍样本标准差(可以不为整数倍数)所形成的上下界曲线与标准样本曲线的距离，作为判断待分类像元是否归属目标类别的标准。可以通过改变标准差倍数来改善结果精度，但如果需要达到满意的精度，该方法所使用的上下界曲线范围内包含的样本数目并不确定，可以很小，此时上下界曲线并没有代表性；可以很大，甚至所包含样本数等于样本总数，但此时上下界曲线同样有过于远离样本的可能，相应的所计算出来的距离阈值不再可靠。分位数法是使用可以包含大部分样本的距离作为阈值，相比标准差法，分位数法可以确切知道距离阈值可以囊括的样本比例，所获得的阈值较之更具有代表性，但它的缺点仍旧是所获阈值一般不能囊括所有样本，这点与标准差法较为相似。

试凑法常与其他阈值选取方法结合使用，如标准差法。分位数法也可以看作试凑法。单纯的试凑法所获阈值无法判断其可靠性，尽管可以得到极高的用户或制图精度，但结果的准确性难以判定。

为了解决上述问题，基于本研究提出的MSMA方法，结合分位数法和试凑法，在以样本距离值域上限作为阈值的基础上，做出一些改进：选择样本距离的百分之百分位数作为距离阈值。同时由于本形态相似性距离测量方法存在β偏移倍数调整因子，不同的因子值会有不同的差异放大效果，调整因子大小，阈值同时会相应变化。该方法阈值获取方式不变，始终为该形态距离度量方法计算的样本距离的最大值，保证囊括了所有参与计算的合格样本，具有较强的合理性，同时在调整β参数以获得最佳MSMA模型的过程中，阈值始终处于动态调整之中，增强了阈值的适用性。

2.5 算法实现

为了测试算法的有效性，本研究使用了单季稻、双季稻、森林、城镇、水域共5种不同类型的地表覆被NDVI时序数据进行算法的检验。其中，各自选取样本数量的50%作为各自类型的训练数据集，使用剩余的样本NDVI时序数据作为验证数据集。

模型有效性验证过程如下。

1)模型训练。①对于某种地物，在训练中，随机选取该地物训练集的20%，在每次迭代中，使用MSMA算法获取一次标准样本数据、样本集与标准数据的平均绝对值距离(计算方法如公式(5)所示)及阈值。②将标准样本数据、平均绝对值距离作为输入，结合剩余的所有地物的各自80%训练集的集合，再次使用MSMA算法，获取相似性度量值Dshape。③使用①中所得阈值，对结果进行类别判定，精度计算。④从训练结果中筛选出使得用户精度最大化的β值。

2)模型验证。①将模型训练中④所得β值作为已知条件，随机选取相应地物验证集的20%。使用MSMA算法获取样本标准数据、验证样本集与标准数据的平均绝对值距离(计算方法如公式(5)所示)及阈值。②将标准样本数据、平均绝对值距离及模型训练中所得β值作为输入，结合剩余所有地物类别各自80%验证集的集合，再次使用MSMA算法，获取相似性度量值Dshape。③使用①中所得阈值，对结果进行类别判定，并计算精度。④模型可行性评估。

模型训练过程和模型验证过程相似，但模型验证过程不需要进行迭代计算。

3 结果与分析

3.1 算法有效性检验

训练结果如表6所示，其中β为算法偏移倍数调整因子。由于并非全部训练样本参与训练结果的统计分析，因此参考样本数为80%的训练集样本。

由于本步中最优β值对应下的各类地物归属判断均为独立的算法实现，故表6、表7均为非混淆矩阵。同时算法的初步有效性检验是在5种已经确定类别的样本点集间进行，以算法对5种地物的分辨能力来判断算法有效性与否，因此此处认为不存在混合像元。混合像元问题在本文中仅存在于对仙桃市单季稻的提取中。单季稻是仙桃市最为主要的粮食作物，通过仅对单季稻信息提取，可以最大限度地减小混合像元的影响。

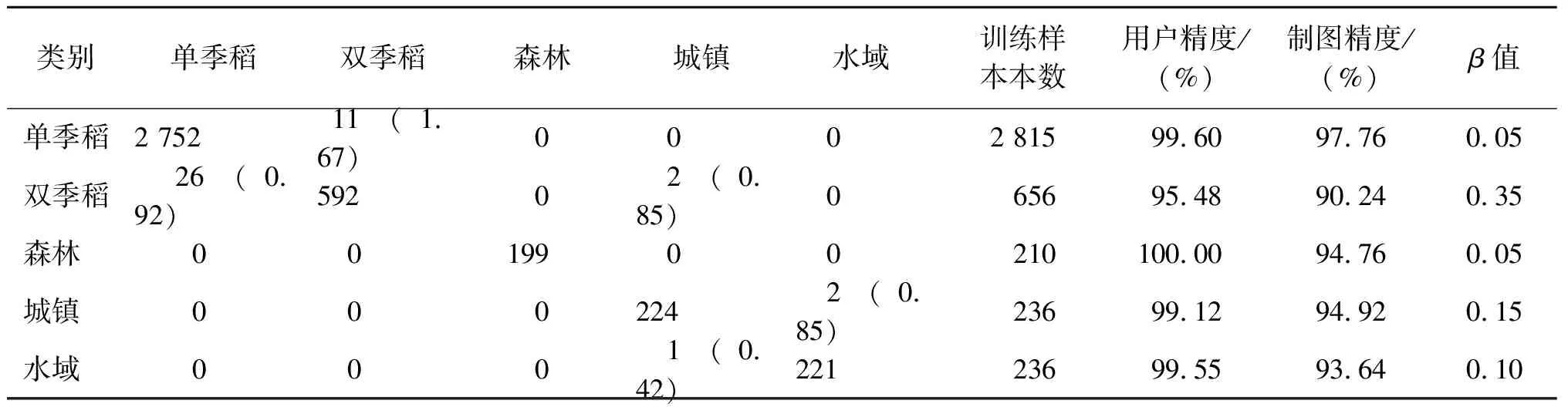
表6 形态相似性度量算法训练结果

注：表中每行表示对训练中所有地物类别对应的各自80%训练集的集合进行该行对应地物的样本类别归属判断；括号中数字为该列对应类别样本错分为该行对应类别的样本所占百分比。

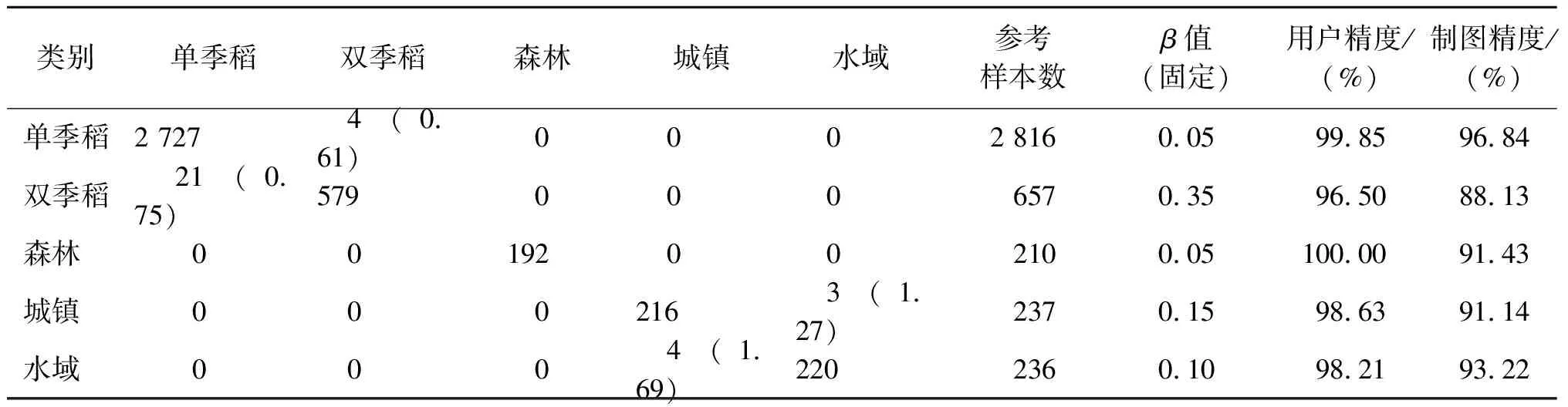
表7 形态相似性度量算法验证结果

注：表中每行表示对验证中所有地物类别对应的各自80%验证集的集合进行该行对应地物的样本类别归属判断；括号中数字为该列对应类别样本错分为该行对应类别的样本所占百分比。

在算法实现中，可以通过调整β值来改变检测精度。由于算法是采用指数映射形式来增大测试曲线与标准曲线的差异，因此β的值不能过大，否则偏移映射值将超出算法检测范围，导致精度的降低甚至算法无效。

本研究中β值设置为0～3之间，间隔值为0.05，理论上每个地表覆被类型测试集将进行60次迭代测试(但当精度提前达到设定精度阈值，将终止迭代)，选取使用户精度最为接近100%的β值，作为算法最终偏移倍数调整因子。

表6中可以看到，算法的偏移倍数调整因子最小为0.05，最大为0.35，此时5类地表覆被类型算法判分结果的用户精度基本均接近100%。其中，森林参考集中完全没有被错分为其他4类地物的样本，其他4类地物同样完全没有样本被错分为森林，说明MSMA算法对森林与其他4类地物之间具有完全的分辨能力。在单季稻类别归属判断时，双季稻参考集中有11个样本被错分为单季稻，错分比例为1.67%，其他3类完全没有被错分样本，说明MSMA算法对单季稻与森林、城镇、水域之间具有完全的分辨能力，单季稻和双季稻之间具有较强的分辨能力。在双季稻类别归属判断时，单季稻参考集中错分样本最多，但错分比例仅为0.92%，城镇参考集中仅有2个样本被错分为双季稻，错分比例依然较低，为0.85%，水域和森林完全无错分样本，说明此时MSMA算法对双季稻与森林、水域之间具有完全的分辨能力，双季稻和城镇、单季稻之间具有较强的分辨能力。在城镇类别归属判断时，仅有水域参考集中存在错分样本，错分比例为0.85%，在水域类别归属判断时，仅有城镇参考集中存在错分样本，错分比例为0.42%，说明MSMA算法对城镇、水域与单季稻、双季稻、森林之间具有完全的分辨能力，城镇与水域之间具有较强的分辨能力。对于制图精度而言，5种地表覆被类型测试结果相对用户精度较低，但同样达到了较高水平，其中单季稻的制图精度最高，达到97.76%，双季稻制图精度最低，为90.24%。

对错分情况分析发现，错分事件在5种地表覆被中基本仅发生在单季稻和双季稻，城镇和水域之间，尽管存在样本数量过少和偶然情况(如测试集的选取是随机的，每次的选取结果均不尽相同，这很有可能导致测试结果的差异)的影响，但这也同样说明了单季稻和双季稻之间，城镇和水域之间的混淆概率相较其他组合较大。

对每种地物样本NDVI时序数据进行异常值剔除，之后进行取平均操作，获取5种地表覆被类型标准NDVI曲线如图2所示。分析发现，单季稻和双季稻所在耕地均为一年两季耕作模式，一年中会有2个时期为作物生长旺盛期，此阶段NDVI值最大，因而其NDVI时序曲线存在2个波峰；而由于森林的生长不同于作物的种植，其生长期较长，受人类活动影响较小，因此在一年中仅存在一个阶段为生长旺盛期，且该阶段较长，因此其NDVI时序曲线仅存在一个波峰，与作物差异明显，并且森林的NDVI值长期处于高值；相较于作物与森林，城镇和水域在时间上的光谱响应最为迟钝，其光谱响应的敏感程度较低，基本仅与光强的大小成正相关，表现为NDVI值整体较小，NDVI时序曲线趋势与光照强度变化一致。因此，5种地表覆被中，城镇和水域的NDVI时序曲线最为相似。这可能为单季稻和双季稻、城镇和水域易混淆的原因之一。

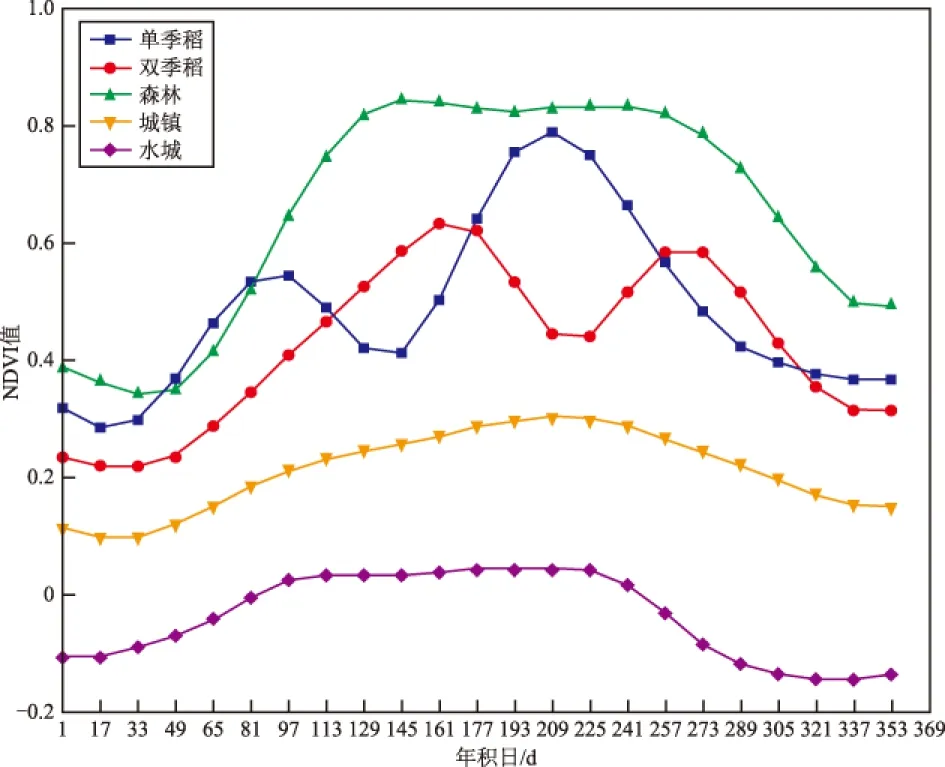
图2 各地表覆被类型NDVI标准时序曲线

表7为MSMA算法验证结果。可以看到，各类地物错分事件分布基本与训练情况一致，仅是数目有所差别。在β值固定的条件下，单季稻和双季稻用户精度有所上升，分别为99.85%和96.50%，森林用户精度保持不变，城镇和水域用户精度有所下降，但基本稳定；对制图精度而言，5种地物均有所下降，其中双季稻最低，制图精度为88.13%，但仍然较为理想，单季稻制图精度最高，为96.84%。总体而言，MSMA模型训练和模型验证前后用户精度和制图精度保持稳定，说明了MSMA算法具有一定的稳健性，在地物分类领域具有操作的可行性。

为了进一步验证MSMA算法可靠性，本文同时检验了动态时间弯曲距离方法(DTW)对5种地物的分辨能力，使用的数据与MSMA算法验证样本相同，并使用分位数法作为阈值获取方式，在不同分位数水平下，各类样本错分情况如图3所示，用户精度及制图精度结果如表8所示。从表8可以看出，随着分位数的增长，制图精度随之增大，当分位数为95%时，制图精度均在90%以上；而对于用户精度，水域和单季稻表现较好，其他3种地物则基本在50%以下；5种地物中，唯有水域的用户精度和制图精度均保持较高水平，森林的用户精度最低，一直保持在10%以下，双季稻次之，保持在20%左右。

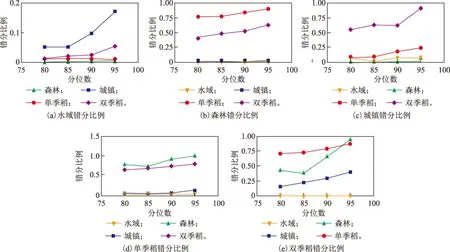
图3 不同分位数水平下各类地物样本错分比例(DTW方法)

表8 不同分位数水平下DTW方法分类精度对比 %

由图3分析知，在从样本集中对森林进行识别时，存在大量的单季稻和双季稻样本被分为森林类别，在对单季稻进行识别时，则有大量的森林和双季稻被分为单季稻。而对于水域，各类地物则有着相对较小的错分比例，当分位数为90%以下时，水域错分为各类地物的比例均低于10%，各类地物被错分为水域的比例同样较低。可见，他类样本的大量错分是各类别用户精度低下的直接原因。

综上所述，在使用DTW方法对5种地物NDVI时序数据进行分类时，水域与其他4类有着最大的时序差异；而除水域之外的4种地物则具有较小的时序差异。这是因为，DTW方法原理即是通过对时间序列的伸缩来最小化未知时序数据与标准时序数据差异，其注重时序空间上的时序曲线的形态，而对位置要求不高。由图2可知，在本次实验中，5种地物的NDVI时序曲线均呈现单峰或双峰特征，而由于DTW度量2条曲线的相似性时，并不是严格的特征一对一匹配，而是伴随着错位匹配，导致了除非地物时序曲线在取值上有着较大差异；否则在使用DTW方法度量时，单峰和单峰曲线、单峰和双峰曲线间及双峰曲线间的差异性很容易被DTW方法的错位匹配极大程度地降低，最终导致结果的不可靠。

3.2 单季稻提取及精度评价

从表7可知，当β值固定为0.05时，单季稻用户精度和制图精度均达到较高水平，可以最大限度地将单季稻与其他地物区分开来，因此在单季稻的提取中，使用0.05作为β值的最优值。仙桃市各年单季稻样本数量如表5所示。单季稻提取步骤如下。

1)随机将各年样本分为80%和20%的样本集1和样本集2。

2)基于样本集1，第一次实现MSMA算法，以得到相应年份的标准单季稻NDVI曲线、平均绝对值距离Dmean(i)，i∈(1，2，3，…，n)，及阈值。

3)将标准单季稻时序曲线、平均绝对值距离与β值作为输入，第二次实现MSMA算法，计算各年单季稻相似性度量值Dshape。

4)使用各年20%的样本验证结果的可靠性。

5)制图。

表9为按照以上步骤，得到的精度验证结果。从表9可以看出，11年中，单季稻提取制图精度基本达到90%以上，其中低于90%的有2年，2009年制图精度最低，为84.21%，2008年和2014年制图精度最高，均为97.30%，11 a总体精度达到93.29%，说明基于MSMA的单季稻提取效果较好。

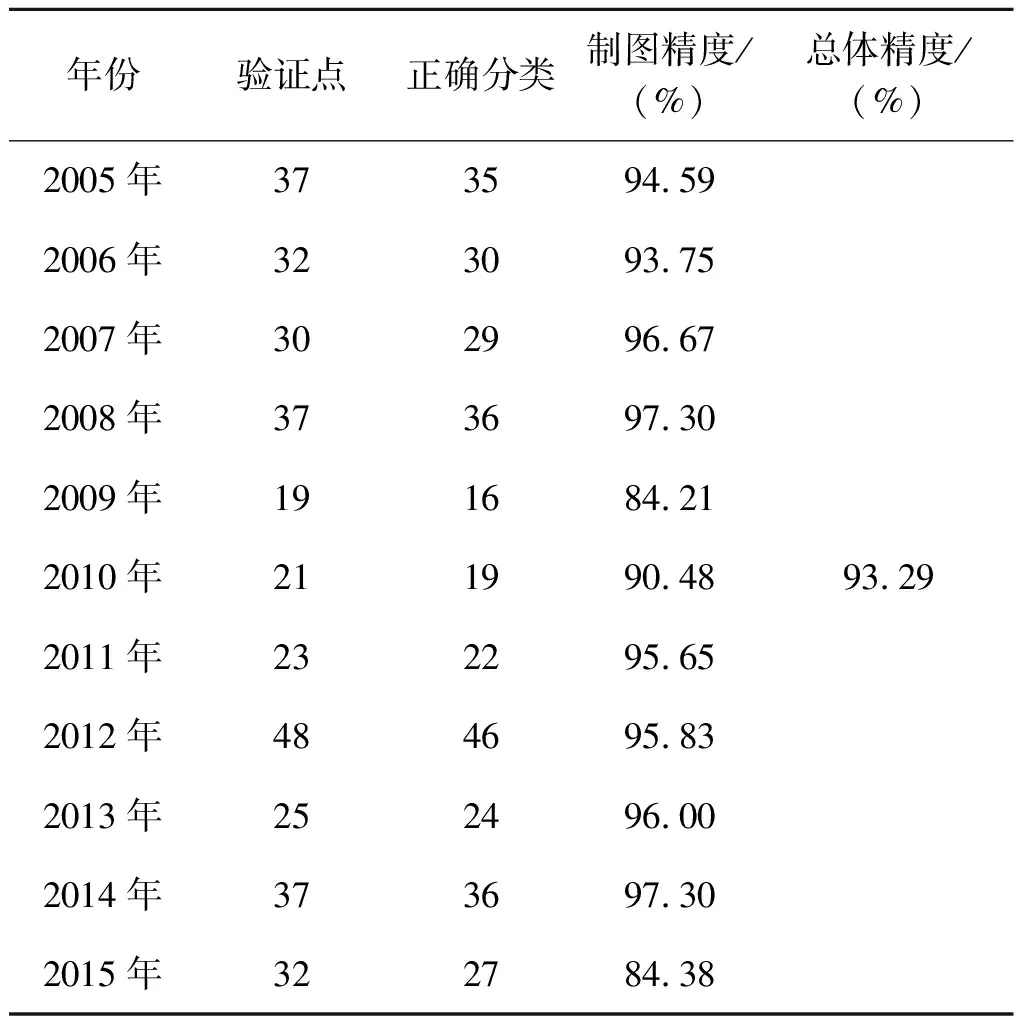
表9 2005—2015年仙桃市单季稻空间提取精度

表10为仙桃市11 a间单季稻面积提取结果。可以看到，与空间提取精度相比，面积提取精度明显偏低，11 a中，有6个年份面积精度低于80%。2015年面积提取精度最高，接近86%，2008面积提取精度最低，为74.57%。面积精度偏低的原因主要源于混合像元的存在，有3种形式：①本文假设不同地表覆被具有不同的NDVI时序曲线，通过衡量不同覆被NDVI时序曲线的相似性来区分不同的覆被类型，但由于作物物候期重叠现象的存在，如棉花与中稻几乎具有相同的物候特征(表1)，同一种NDVI时序曲线可能表示多种地表覆被类型，导致提取的面积数据一般大于统计数据；②本文所用遥感数据时间分辨率为16 d，这使得本来不具有相同物候特征的植被类型，在遥感影像上反而可能表现出相同的物候特征，从而导致了混合像元的产生；③本文所用遥感数据空间分辨率为250 m，空间异质性低，每个像元可能包含多种地表覆被类型，是混合像元产生的最主要原因。因此，虽然表10所示面积精度提取结果较低，但符合实际情况，也从面积上验证了MSMA算法的有效性。

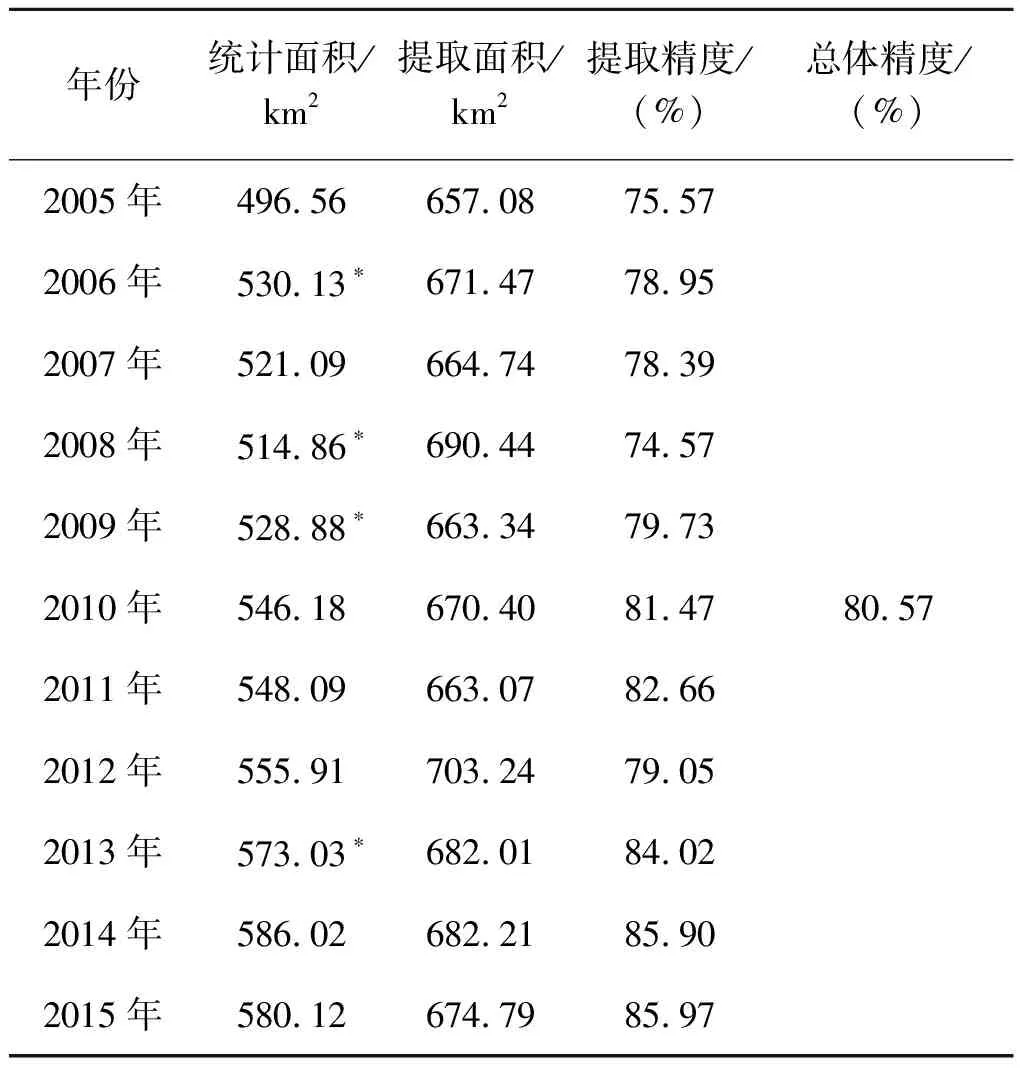
表10 2005—2015年仙桃市单季稻面积提取精度

注：由于仙桃市年鉴收集不全，统计面积中带*号的数据为基于当年稻谷总产量、中稻单产、中稻占稻谷总产量一般比例推算得到。

使用MSMA算法对仙桃市单季稻提取结果分析发现，仙桃市单季稻种植基本分布全境，其中，仙桃境内中西部、中北部、东南部在11 a的提取结果中均有较大的空白区域出现。中西部空白区域为仙桃稻虾养殖区域，由于水稻收割之后需要灌水以形成虾类的生存环境，一年中除了中稻生长时期，基本被水覆盖，因此该类地表覆被类型NDVI时序曲线既不同于单季稻，也不同于水域。本研究中对单季稻样本的提取是基于中稻与其他作物(小麦、油菜等)连作的假设(这正是一般情况)，因此虽然稻虾养殖模式仍然可看作单季稻模式，但在提取结果中却未能把稻虾养殖区域判分为单季稻区域。同时在2005—2010年，该地区稻虾养殖区域逐渐扩大，之后逐渐缩小。

11 a间，在仙桃各地区中，西北部单季稻种植变化最为明显，2005年、2009年、2014年均有较为显著的变化。根据天地图判断，东南部为仙桃市滩湖所在，靠近长江，周围鱼塘较多，并且同样存在稻虾养殖模式，使得单季稻判分错误。至于中北部空白区域，则为仙桃市区所在，在11 a中，该区域有明显的扩展，与城市化进程相符。整体而言，11 a间仙桃市单季稻种植空间分布基本稳定。

4 结束语

基于本研究所提出算法，对仙桃市单季稻区域进行提取，总体制图精度为93.29%，总体面积精度为80.57%，达到较高水平，证明了MSMA算法的可靠性。MSMA算法相较于其他相似性度量算法有以下优点：

1)相较于动态时间弯曲距离算法，MSMA更易于实现，复杂度较低，分类精度更高。

2)相较于欧式距离的特征差异简单累加，MSMA算法基于特征差异动态调整思想，增强了对不同地类的区分能力。

3)陆俊等[12]基于STDFA数据融合模型和SVM算法得到的水稻制图精度达到94%;而MSMA算法以更低的实现复杂度，达到了相似的效果。

虽然MSMA具有诸多优点，但本研究仍然存在一些问题：

1)本研究中单季稻样本的获取是基于小麦/油菜-中稻模式的物候期特征获取的，虽然这种模式在研究区为主要作物种植模式，但仍然存在其他模式具有相似的物候期特征(如小麦-棉花模式)，因此提取的单季稻样本中包含一定的其他作物模式的样本，这使得结果的可靠性下降。

2)本研究使用的数据为MOD13Q1数据集，其中NDVI数据空间分辨率为250 m，因此空间分辨率低下导致的混合像元的存在将是影响提取结果可靠性的另一重要因素，混合像元的分解将能进一步改善分类效果。

3)MOD13Q1数据集中NDVI数据时间分辨率为16 d，时间分辨率较低，不能保证可以获取水稻淹水期NDVI数据;而水稻淹水期NDVI特征是区分水稻与其作物的重要物候特征，这使得单纯使用作物NDVI时序曲线，依靠作物时序上的特征提取作物空间分布存在局限。

在算法有效性检验和后续单季稻提取中，MSMA均有着较好的表现，说明了该算法的有效性。一旦上述问题得到解决，相信使用该算法获得的目标类别提取结果会具有更高的可靠性。