基于GPS-IR的土壤湿度多星非线性回归估算模型

任超，潘亚龙，梁月吉，张志刚，黄仪邦

(1.桂林理工大学 测绘地理信息学院，广西 桂林 541004；2.广西空间信息与测绘重点实验室，广西 桂林 541004)

0 引言

土壤湿度值是水文、气象和农业环境研究中的重要参数。对于土壤湿度长期监测来说，传统方法存在成本高、处理操作复杂、适用范围有限等缺点[1]。目前，基于测量型接收机发展起来的GPS-IR技术已经成为了一种具有低成本、高效率、高分辨率的方法，被广泛应用于监测海冰、海平面、雪深、土壤湿度等方面[2-3]。

目前国内外利用此技术在反演土壤湿度方面已经进行了大量研究。Larson等[4]利用GPS观测文件中的信噪比(signal noise ratio，SNR)进行土壤湿度监测的研究，表明反射信号的振幅与土壤湿度的总体变化趋势吻合度较好。Zavorotny等[5]建立了一个GPS值反射信号干涉的物理模型，模拟土壤湿度变化对多径干涉相位和振幅的影响。Chew等[6]利用上述模型进行模拟实验，结果表明反射信号的多径干涉相位与表层土壤湿度线性相关，是估算土壤湿度的最佳参数。敖思敏等[7]指出SNR多径干涉相位与土壤湿度之间存在指数关系。丰秋林等[8]提出利用BP神经网络估算土壤湿度相较于线性回归模型具有明显的优势。但是综合已有研究，目前利用GPS-IR技术反演土壤湿度更多局限于采用单星反演，较少研究多星联合反演土壤湿度方面。考虑到多卫星的利用，Ren等[9-10]研究发现，多星融合反演土壤湿度相较于单星反演有了较为明显的提高，但对模型的建立仅局限于机器学习方法，不易于模型的可视化。因此，本文围绕GPS多星联合反演的问题，建立一种多星非线性回归模型，并通过与土壤湿度参考值对比分析，验证本文模型反演土壤湿度的可行性和有效性。

1 土壤湿度反演原理

1.1 GPS-IR基本原理

GPS-IR技术的核心是SNR，SNR主要受天线增益参数、多路径效应和接收机中随机噪声等因素的共同影响。在低卫星高度角的情况下，SNR受多路径的影响较大。

Chew等[11]的研究表明，SNR观测值与多径干涉相位之间是一种正弦(余弦)关系，而利用GPS-IR监测土壤湿度只与反射信号相关，那么去除直射分量后的SNR只剩下多路径反射分量，其与sinθ之间仍存在某一固定频率的正弦(余弦)函数关系。一次反射假设下，多路径反射分量SNRMP2为卫星高度角的函数，其表达式见式(1)。

(1)

式中：θ、λ、H分别表示卫星入射高度角、载波频率和天线高；AMP2、ΦMP2分别表示多路径反射分量的振幅和多径干涉相位。若记t=sinθ,f=2H/λ，则式(1)可以表示为式(2)。

SNRMP2=AMP2cos(2πft+ΦMP2)

(2)

1.2 多星非线性回归模型

敖思敏等[7]指出多径干涉相位与土壤湿度之间存在指数关系，那么二者之间是否还存在其他的非线性关系，这成为了本文研究的出发点。

多元非线性回归分析方法适用于解释一个因变量与多个自变量之间的非线性关系。为了探讨其是否也能够应用于土壤湿度反演方面，本文建立了一个土壤湿度y与各卫星反演出的干涉相位xi(i=1,2,…,n)之间的多星非线性回归模型[12]，表达式如式(3)所示。

(3)

式中：b1为回归系数；bm为偏回归系数(m为正整数)。采用列文伯格-马夸尔特(Levenberg-Marquardt，L-M)方法[13]对多星非线性回归方程的回归系数进行求解。

1.3 反演流程

1)分离直反射信号。采用TEQC软件解算GPS观测数据，得到L2载波的SNR值，并通过二次多项式拟合分离直反射信号。

2)信号重采样。对随历元变化的反射分量进行重采样，转化为与卫星入射高度角正弦值sinθ之间的关系。

3)参数估计。采用非线性最小二乘拟合法对重采样后的分量进行正弦拟合，得到干涉相位，并采用L-M方法求解多元非线性回归模型的参数。

4)建立模型。输入样本数据，并采用L-M方法求解多星非线性回归模型的回归系数，建立多星非线性回归模型，并利用测试数据检验模型反演精度。

2 实验分析

实验使用美国板块边缘观测观测计划(plate boundary observatory，PBO)(www.unavco.org)提供的P041站2011年年积日131～271 d的GPS观测数据和土壤湿度参考值，该站接收机为TRIMBLE NERT9，采用SCIT的天线罩，天线型号为TRM59800.80，数据采样频率为15 Hz。

本实验使用L2载波上高度角5°～20°之间的SNR数据进行反射信号参数估计：首先利用TEQC解算出L2载波信号的SNR数据；然后经过二次多项式拟合分离卫星的直反射信号，并采用非线性最小二乘拟合得到各个卫星的多径干涉相位。由于一年内各卫星的运行轨迹没有较大的变化，本文尝试选取PRN6、7、12、17、20、24、32卫星反射信号的多径干涉相位进行研究，以及利用各卫星在年积日131 d的方位角和截止高度角探讨各卫星的菲涅尔反射区[14]与干涉相位之间的关系，结果如图1、图2所示。

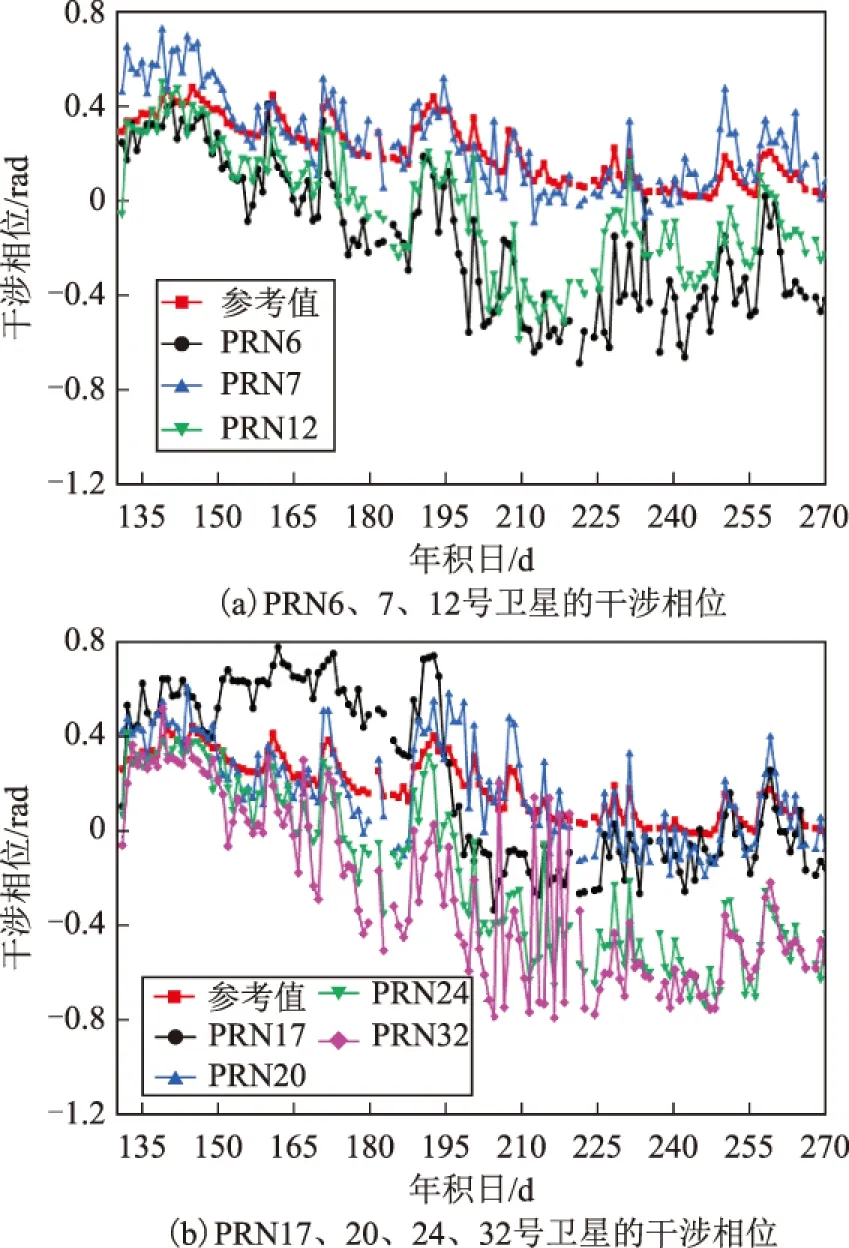
图1 部分卫星的干涉相位

从图1可看出，干涉相位能对土壤湿度的变化做出响应，但不同卫星具有不同的干涉相位，且大部分卫星的干涉相位与土壤湿度之间存在较大误差，异常跳变值较多。从图2可看出，大部分卫星在同一天的菲涅尔反射区域不重叠，仅有PRN6和PRN24的菲涅尔反射区域具有较高的重叠度。结合图1可以发现，二者干涉相位的变化相似，进一步分析发现，二者干涉相位的相关系数r达到了0.9。综上所述，各卫星的干涉相位与土壤湿度偏差各异，这主要是由于各卫星截止高度角和不同方位角所造成的。那么如何通过建立多星非线性回归模型充分发挥各卫星的优点，以获取更为精确、可靠的土壤湿度值，成为了本文研究的重点。

本文选取7颗卫星在年积日131～245 d的干涉相位作为建模的输入样本，并通过L-M方法求解出式(3)中的回归系数，建立多星非线性回归模型。然后，利用年积日246～271 d的干涉相位作为测试样本，以检验模型的可行性。各建模方案的回归系数如表1、表2、表3所示，图3给出了不同方案的土壤湿度反演结果。

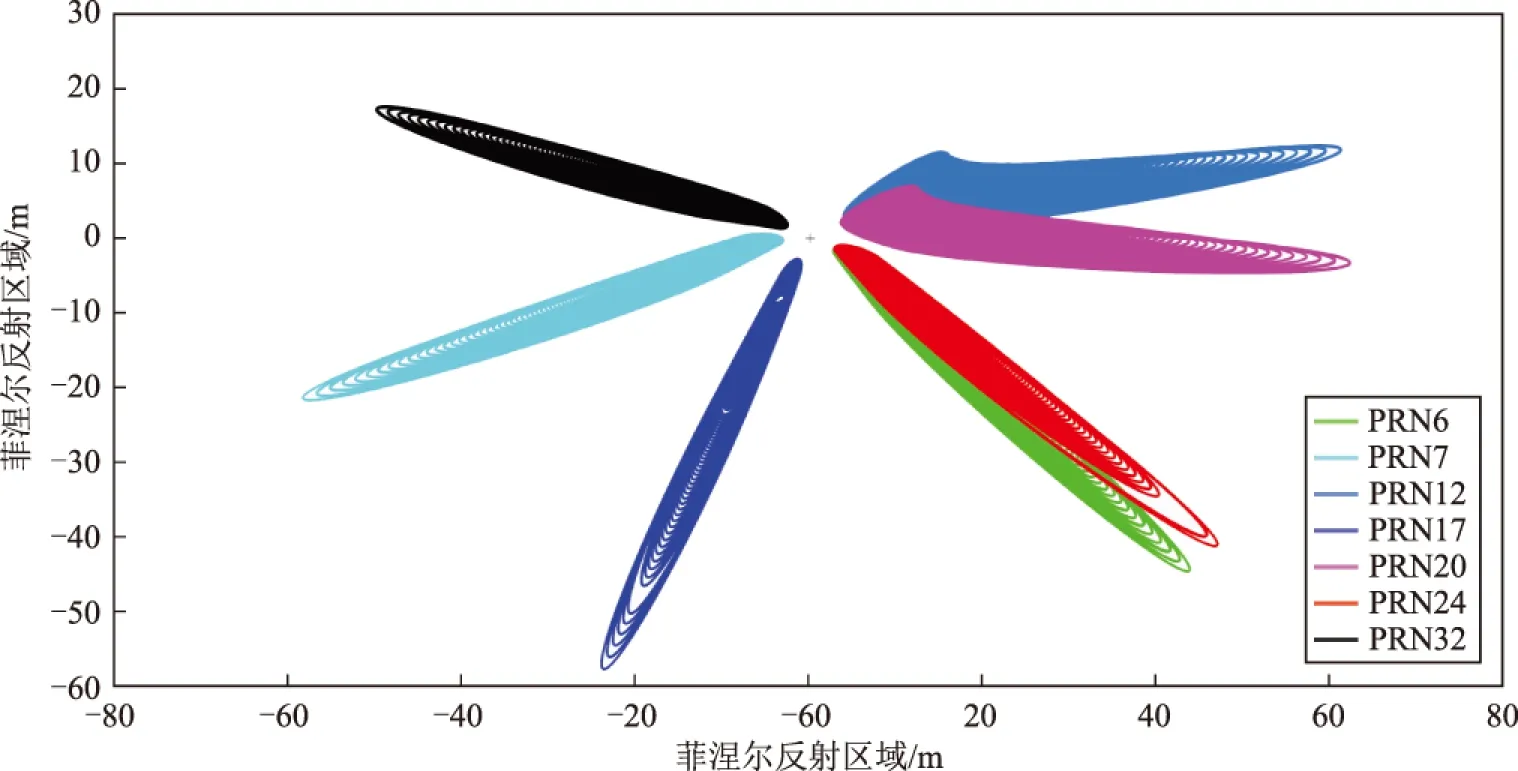
图2 部分卫星的菲涅尔反射区域

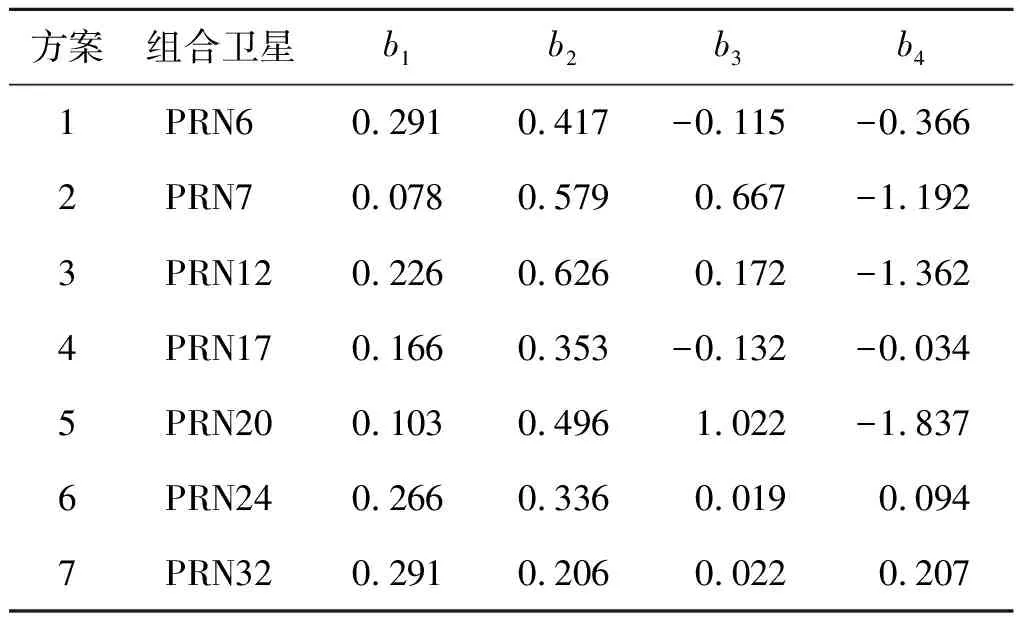
表1 单星非线性回归模型回归系数

从图3可知，单星建模反演误差较大，且存在很多异常跳变值，如PRN17、20、32等卫星在年积日210～220 d这段时间出现了较多的异常跳变值。通过分析得出，这些出现异常跳变的卫星都是原始干涉相位与土壤湿度相关系数较低的卫星。而采用双星建模的效果明显优于单星，能较为准确地反映出土壤湿度的变化。三星建模的效果最好，反演结果与土壤湿度具有很强的相关性，且异常跳变值得到了有效的改善，建模误差和测试误差均取得了很好的改善。

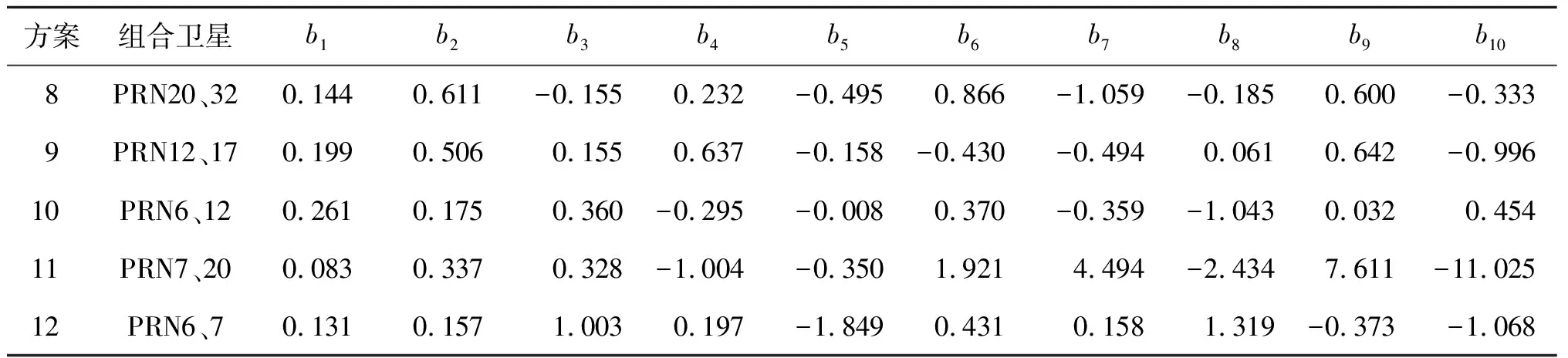
表2 双星非线性回归模型回归系数

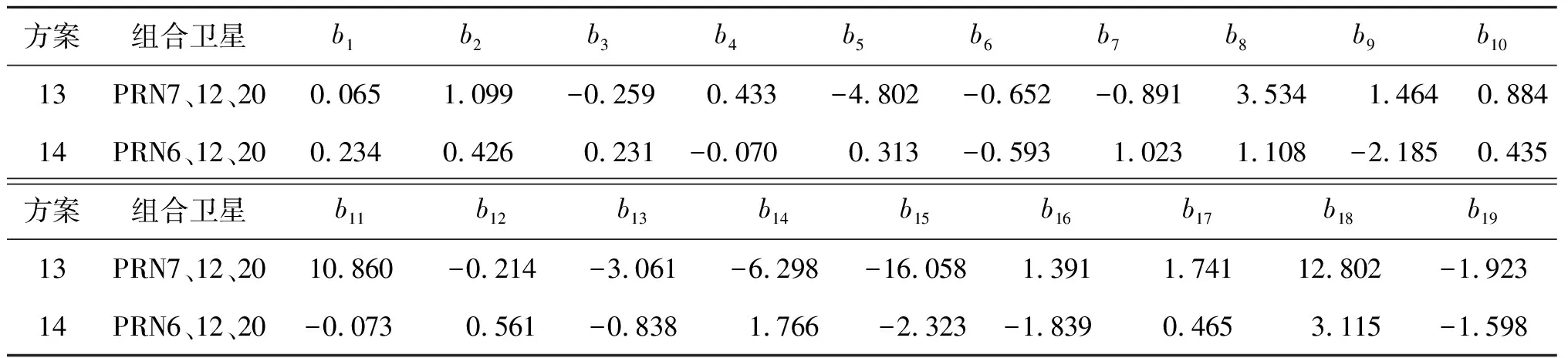
表3 三星非线性回归模型回归系数

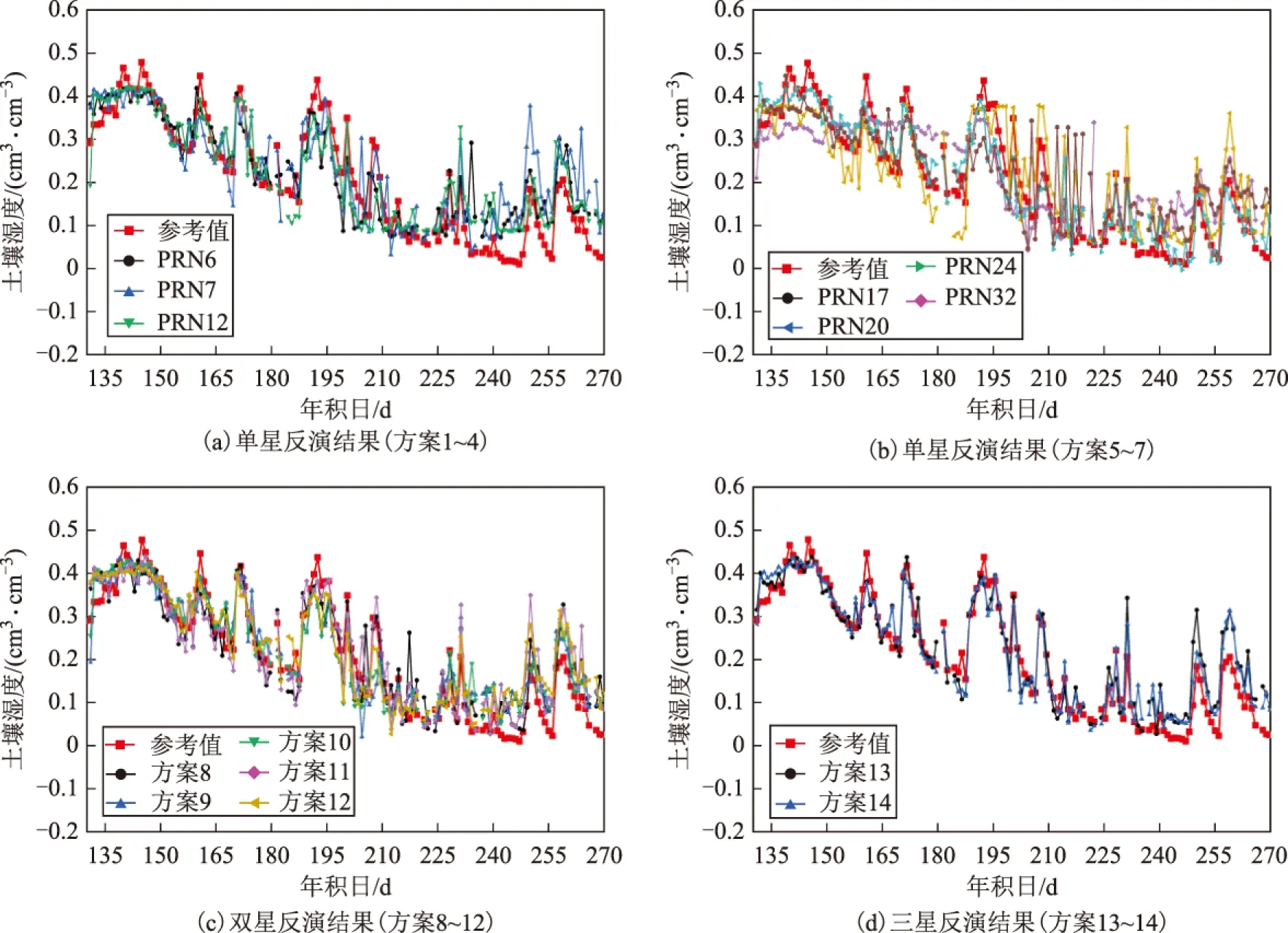
图3 各方案反演土壤湿度结果

为了进一步综合评定各建模方案的可行性和有效性，本文采用相关系数(r)、均方根误差(root mean squared error，RMSE)、平均绝对误差(mean absolute deviation，MAD)对模型的建模(内符合)和测试(外符合)精度进行综合评定。各方案精度指标如图4所示。

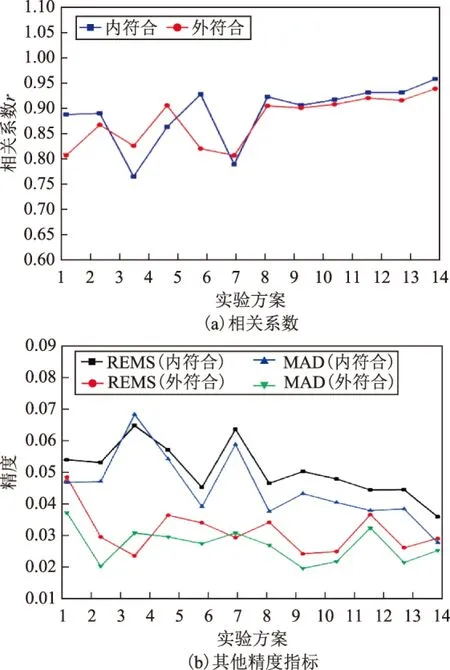
图4 各方案精度指标

从图4分析可得，由于各卫星性能的差异，采用单星建模反演土壤湿度时，反演结果不尽相同，且精度指标较差。而采用双星和三星建模时均取得了较好的效果，反演结果与土壤湿度之间的相关系数r分别达到了0.90以上和0.93以上，其测试部分的RMSE平均值分别为0.029和0.026。

综上所述，不同卫星对于土壤湿度的反演结果不同，采用单星建模并不能很好地表现土壤湿度的变化，且模型精度较差；而采用双星或三星建立的多星非线性回归模型能充分融合各卫星的优势，所反演出的干涉相位与土壤湿度具有很强的相关性，且模型精度较高。

3 结束语

本文提出了一种多星非线性回归模型，经过理论和实验分析得出：①本模型较好地融合各颗卫星的优点，能很好地反映出土壤湿度的变化，有效改善了采用单星反演结果容易出现异常跳变的现象。②采用双星或三星联合建模反演时，相关系数r分别达到了0.90和0.93以上，测试结果相对于单星平均提升了18.3%和21.5%，RMSE平均值分别达到了0.029和0.026。③对于如何通过卫星的方位角和截止高度角选取较优的卫星建模，以及采用4颗以上卫星组合建模效果如何，这些问题仍需要进一步深入研究。