配套使用电感试验和抗折试验对钢纤维混凝土力学特性及纤维分布的研究*

申俊敏

(1.同济大学道路与交通工程教育部重点实验室 上海 201804； 2.山西交通控股集团有限公司 太原 030006)

在过去的几十年里，钢纤维混凝土(SFRC)的应用研究得到了快速发展。在混凝土中加入钢纤维可增强混凝土构件的抗疲劳能力及开裂后的承载力等。鉴于钢纤维混凝土的这些优良性能，使得用钢纤维部分甚至全部取代传统钢筋作为混凝土的加强筋成为了一种可能。随着建筑行业熟练工人的逐步减少，要建设高质量的混凝土结构变得越来越难，为解决这些棘手的问题，自密实混凝土(SCC)于1988年在日本应运而生[1]。鉴于其在人力成本，安全性能及噪音污染等方面的显著优势，SCC自发明以来就受到了世界各国专家学者的青睐。在SCC里加入钢纤维形成钢纤维自密实混凝土(SFRSCC)，可以同时具备SFRC和SCC的共同优点，因此，关于SFRSCC的研究自其第一次在实际工程中应用以来，就一直进行中[2]。为了确保SFRC的质量，对于钢纤维混凝土的裂后性能及纤维含量的评估是十分重要的。通常情况下，SFRC的裂后性能使用三点或四点抗折试验结果表征；另一方面，纤维含量是根据规范UNE-EN 14721[3]所使用的方法来进行的。然而，在所用方法中，要测得钢纤维的含量，必须碾碎SFRC试件或对新拌混凝土进行清洗，从而分离出纤维来进行称重。完成这些流程，不仅程序繁琐而且价格昂贵，单位时间试件测试数量受到严重限制，不能很好地为结构设计提供可靠详实的数据。

本文的研究目的在于，结合电感试验和三点抗折试验结果，提出一种钢纤维混凝土质量控制更有效的替代方法。首先，对普通钢纤维混凝土(CSFRC)和钢纤维自密实混凝土(SFRSCC)进行三点抗折试验以表征其裂后性能；然后，利用电感试验对浇筑的立方试件和从小梁切割出来的立方体试件进行纤维含量及纤维分布的评估。最后，进一步分析以上试验结果，从而对所测试纤维混凝土材料性能给出客观的评价。

1 试验概述

1.1 传统钢纤维混凝土和自密实钢纤维混凝土配比

试验拟制备C60混凝土试件若干，CSFRC和SFRSCC的材料配合比如表1所示，其中GLENIUM TC1425是活性减水剂，X-SEED为早强剂。试验所采用的钢纤维为Master Fiber502，其抗拉强度不小于1 000 MPa，长度为(50±1) mm，长径比为50。

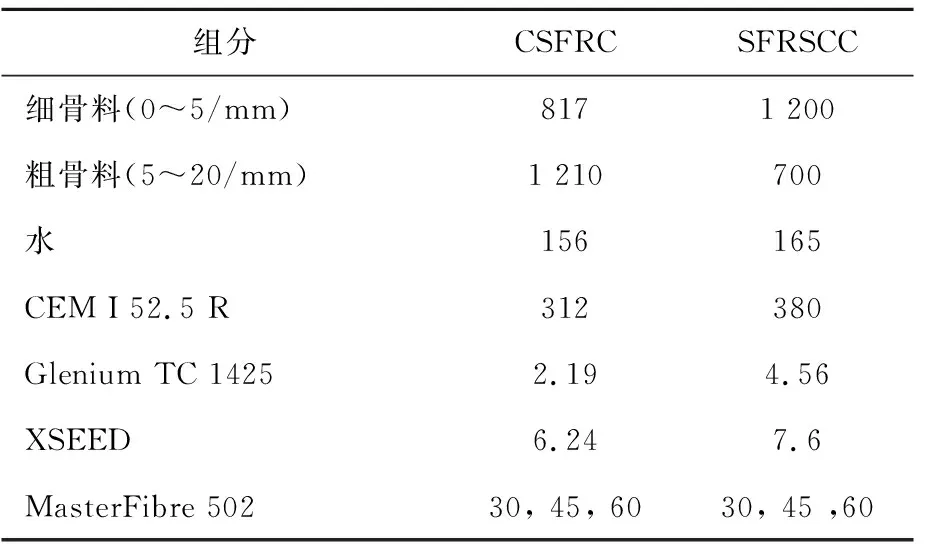
表1 CSFRC和SFRSCC的配合比 kg/m3

1.2 试验测试

分别制作3组纤维含量为30,45和60 kg/m3的CSFRC和SFRSCC试件若干(分别标记为CSFRC-30、CSFRC-45、CSFRC-60和SFRSCC-30、SFRSCC-45、SFRSCC-60)。在试件进行28 d标准养护以后，根据相关规范对硬化混凝土进行如表2中的试验测试[4-5]。最终测试结果均取平均值。

表2 硬化混凝土试验测试项目

1.3 电感试验

电感试验由Torrents等人发明并被Cavalaro等人优化，通过该试验可以初步判定钢纤维在混凝土试件内的分布及纤维数量，其测试所需时间短，可靠度高，能够在短时间里测试大量试件，进而更准确地掌握材料属性[6-7]。

该测试设备见图1a)，它包含由绝缘铜线绕制而成的螺旋管及LCR阻抗分析仪。试验时，通电螺旋管会在其内部产生电磁场，当放入SFRC试件以后，由此所引起的感应电动势变量可通过LCR仪转化为电感强度值显示出来，进而判断出钢纤维在空间不同方向的分布。

在试验过程中，对2类边长为150 mm的立方体试件进行了电感试验。其中一类为150 mm标准立方体浇筑试件；另一类为小梁三点抗折之后进行切割出来的立方体试件，见图1b)。之所以要把小梁两边75 mm混凝土切掉，主要是为了排除钢纤维混凝土“边墙效应”的干扰。对于每一组试件，共8个标准块和6个切割块进行试验，试验结果取平均值。

图1 试验设备及试件(单位:mm)

电感试验的X,Y及Z轴方向测试结果的平均值反映了该轴方向的纤维含量及纤维分布比例。根据Cavalaro的研究表明，SFRC试件的纤维含量和其电感值呈线性关系，因此，可以通过破碎少量试件来得到纤维含量和电感值的关系以进一步预测纤维含量。为进一步校核测试结果，试验结束后任意选取4个测试试件进行破碎，筛选钢纤维称重并精确到0.000 1 kg。采用最小二乘法拟合可得电感强度(L)-纤维含量(Cf)的线性关系，见图2。由图中线性回归系数可以看出，电感试验测试结果能够很好地预测SFRC中钢纤维的含量。

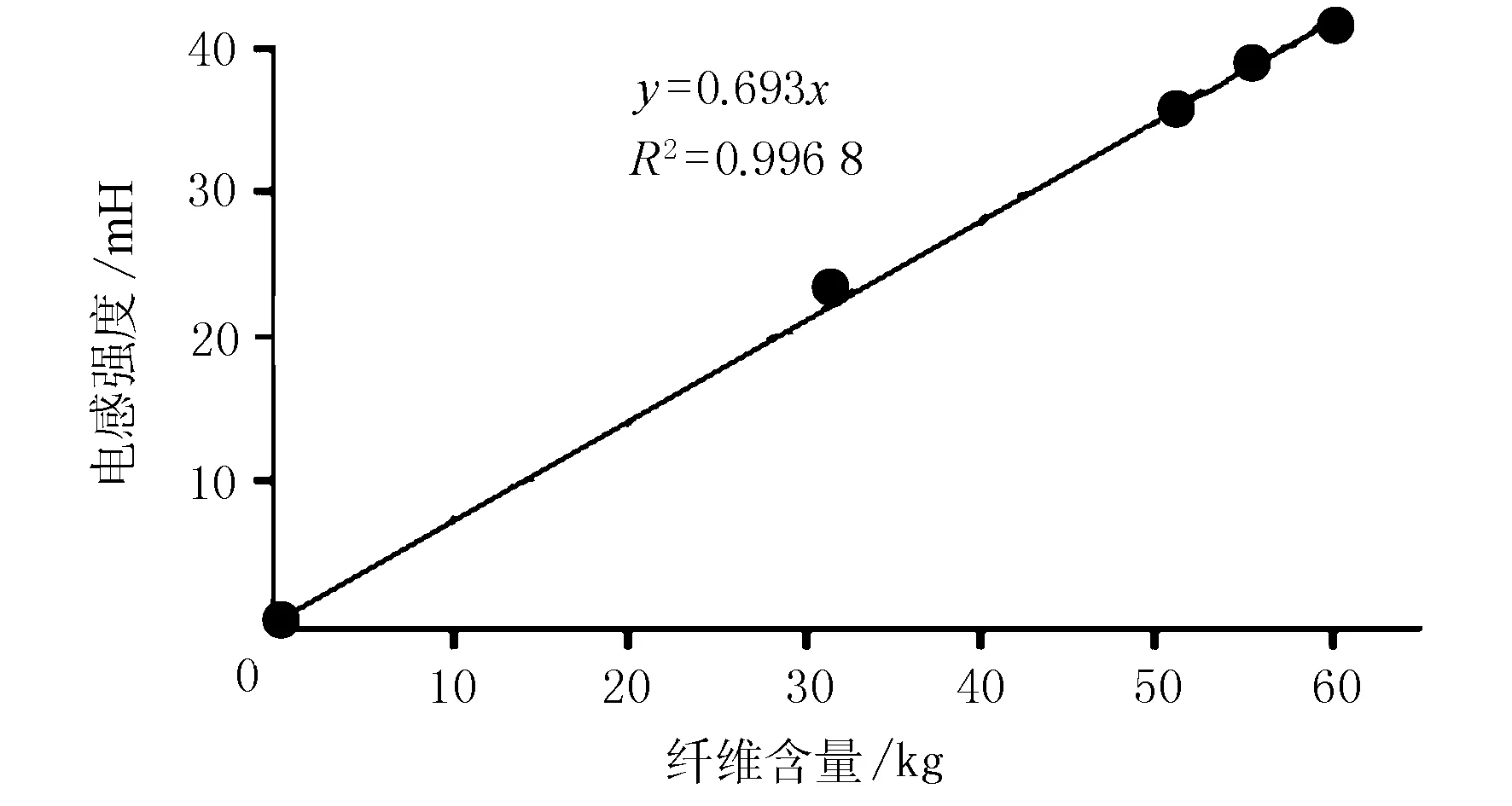
图2 电感强度-纤维含量拟合关系图

2 试验结果与分析

2.1 抗压强度

抗压试验结果见表3。由表可见，CSFRC 28 d的平均抗压强度为64.7 MPa，SFRSCC的为67.5 MPa，比前者稍高。

同时，还可以得出，钢纤维的含量对混凝土抗压强度的影响并不明显；而且纤维含量对测试结果的离散性影响也在可接受范围内(CSFRC 和 SFRSCC分别为1.13 MPa，2.65 MPa)。

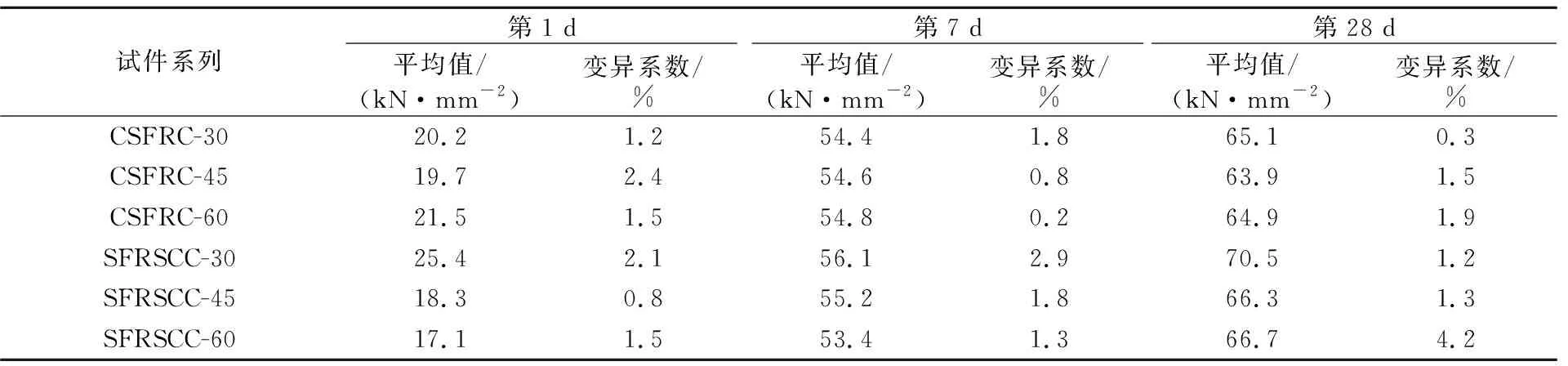
表3 SFRC抗压强度平均值和变异系数

2.2 剩余抗折强度

为了探究SFRC的弯曲性能，根据规范EN 14651∶2005所推荐的方法，对SFRC梁进行了三点抗折试验。根据规范规定，试验过程需要记录峰值荷载fLOP， 开口位移CMOD分别为0.5，1.5，2.5，3.5 mm时试验所对应的荷载强度值F0.5，F1.5，F2.5，F3.5，见图2～图5。混凝土的比例极限强度fLOP及其残余抗弯拉强度fR,j可以根据公式(1)计算得到。三点抗折试验结果F(荷载)-CMOD(开口位移)曲线关系见图3。

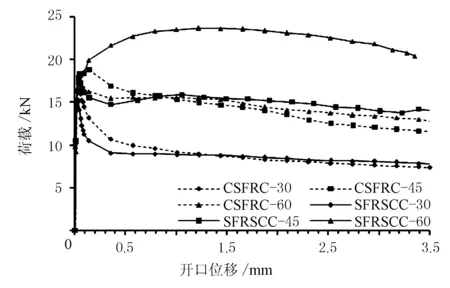
图3 抗折试验测试F-CMOD关系图

由图3可见，荷载强度达到峰值之前，所有试件F-CMOD均表现为线性关系；接着由于试件刚度的突然降低，峰值荷载急剧下降。在SFRC试件开裂后，分散其中的钢纤维开始参与工作，以提升试件的剩余抗折强度。从图3可以看出，SFRSCC总体上比CSFRC表现出更好的裂后性能，在纤维含量为60 kg/m3表现的更加明显。

(1)

式中：b,h分别为试件截面的宽度和高度，均为150 mm；hsp为试件割缝顶到顶面的高度(125±1) mm；L为试验时试件的跨距，500 mm；F为试验时的荷载强度，kN。

从表4中可见，除了纤维含量为30 kg/m3系列外，所有试件的峰值强度(fLOP)差别不大，但是纤维使用量与其峰值强度大小成正相关。另外，SFRSCC比CSFRC具有更好的裂后性能(fR,2,fR,3和fR,4)，这样的趋势随着纤维含量的增加表现地愈加明显。出现这样的结果，主要归咎于SFRSCC良好的流动性会引导钢纤维更多地分布在试件开裂的垂直方向。相反地，CSFRC也许由于其流动性较差原因，不能为纤维分布创造良好的流动环境，故其在混凝土内的分布趋向性不明显。

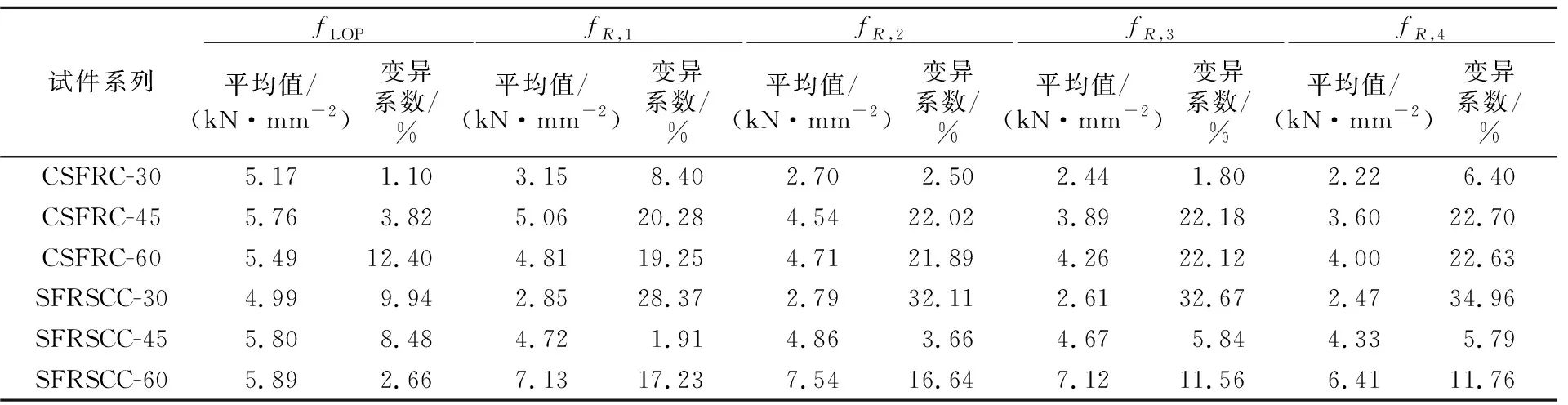
表4 三点抗折平均值和变异系数

2.3 电感试验结果

钢纤维的掺入很容易降低混凝土的流动性。然而，迄今为止也尚不明确钢纤维的增加是否会导致纤维在混凝土内的分布改变。所以，了解纤维含量与纤维分布关系的具体信息对了解和掌握SFRC的性能至关重要。图4为钢纤维不同方向分布关系。其横坐标代表试件的3个轴方向，纵坐标代表各个方向电感值在3个轴所占的比例。

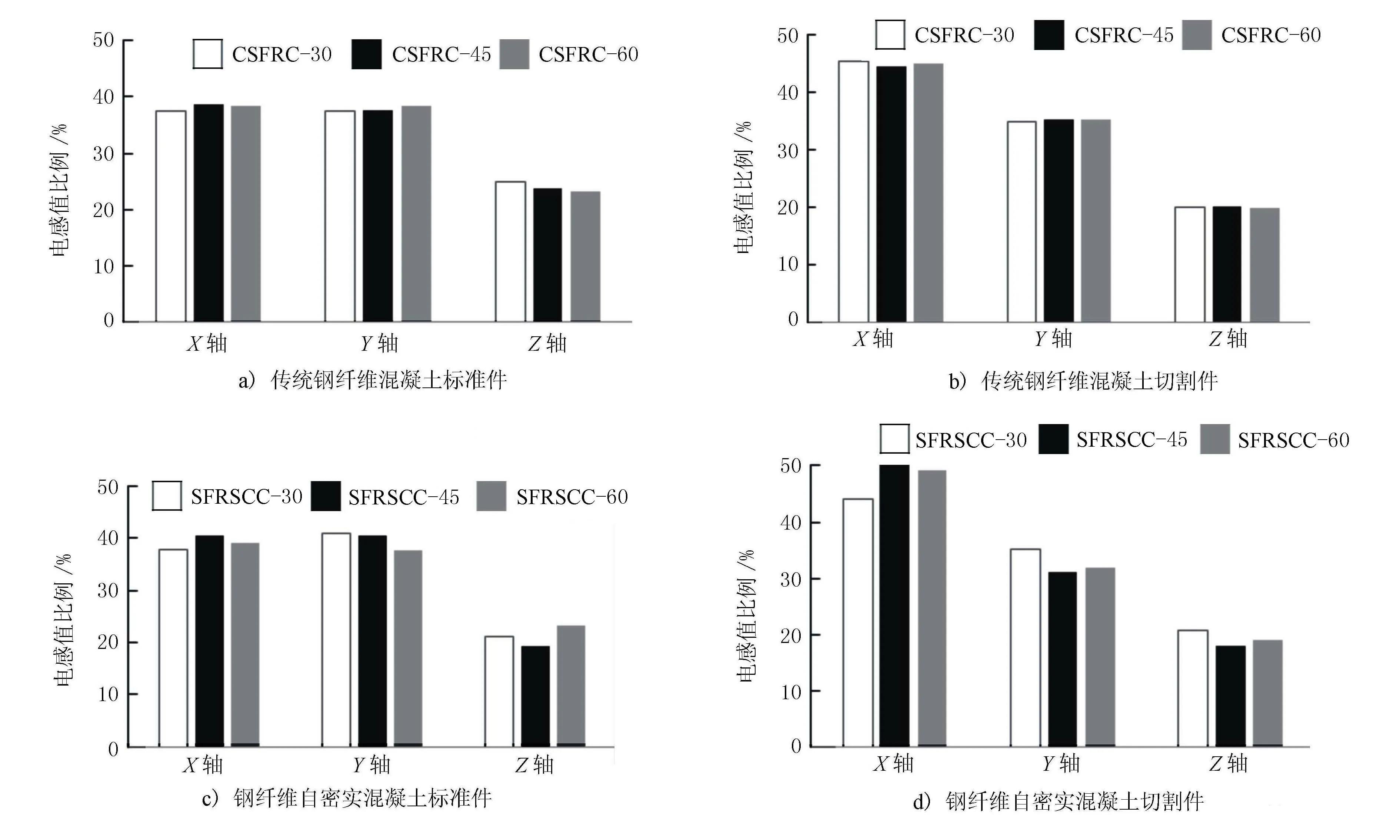
图4 钢纤维不同方向分布关系图

由图4可知，对于浇筑的标准试件而言，X和Y轴方向拥有相似的纤维分布量，且纤维分布数量总是比Z轴大。值得一提的是三者维持在一个基本恒定的比例，即X∶Y∶Z=4∶4∶2。从图4还可知，对于从小梁切割出来的立方体试件而言，X轴方向纤维分布比Y轴略大，两者同时也都大于Z轴方向的纤维分布。三轴方向纤维分布比例也基本为一恒定值，即X∶Y∶Z=4.5∶3.5∶2。综上所述可知，纤维含量的多少不影响纤维在混凝土内部的分布规律。

3 结论

1) 钢纤维的加入有效增加了混凝土的韧性，且SFRC的剩余抗折强度与钢纤维含量成正比。

2) 在钢纤维含量相同的情况下，SFRSCC一般均比CSFRC具有更好的裂后性能。

3) 配套使用三点抗折试验和电感试验分析结果，可以很好地分析SFRC的材料属性及力学性能。

4) 通过电感试验得到的电感值和纤维含量的关系中R2接近于1，表明电感试验对预测钢纤维的分布及纤维含量的评估等方面具有明显效果。

5) 电感试验测得纤维方向系数在X、Y、Z轴方向上的比例大致保持恒定，其与纤维含量关系不大。