基于细观数值试验的水平井多裂纹间距确定
于 友, 魏建光, 李江涛
(1中国石油吉林油田有限责任公司 2东北石油大学非常规油气研究院)
非常规油气储层的多裂缝水平井技术成为油气资源开采的关键核心技术[1-4],由于多裂纹产生的应力扰动现象会影响裂缝的几何形态,比如裂缝长度。水平井设计时首先应当考虑的是射孔间距的优化问题,其中涉及的一个重要现象就是stress shadow效应[3]。
目前大量学者对多阶段水平井水力压裂过程中的应力扰动现象及裂纹间距的影响进行了研究,以提示水力裂纹相互作用的stress shadow效应[5],Fisher等[6]研究发现对储层进行过渡改造时会有应力转移现象的发生,发生应力转移区域中的应力由于局部高流体压力的存在而增大,进而对后面的压裂阶段造成影响。Morrill[7-13]等研究发现stress shadow效应导致储层的激活效果存在明显的差异,多条水力裂纹产生的应力阴影效应与原位应力和施工参数密切相关。本文选用渗流-应力-损伤耦合分析程序,从岩石细观损伤力学角度出发,重点研究岩石材料的细观非均质性对裂纹动态扩展和水平井多裂纹间距的优化问题,为水平井压裂技术提供一定的理论依据。
一、数值模型概化与计算方案
压裂中通常认为降低裂缝间距可以形成更加复杂的水力裂缝网络,从而提高油井产能。而实际上在较小间距下,受“stress shadow”效应影响,部分水力裂缝不能完全延伸或扩展,中间裂纹由于受到的地应力作用相对更强,宽度和导流性将大大受到抑制,必须对应力扰动和水力压裂进行深刻的研究以避免砂堵现象和纵向裂纹的出现,对井孔间距进行优化计算时,本文引入均质度系数来表征储层非均质性,均质度系数越小,储层越均质;均质度系数越大,储层非均质性程度越高。
研究中采用数值计算软件RFPA-Flow[14]建立二维平面应变计算模型,模型中综合考虑了岩石破裂失稳过程中的渗流-应力-损伤特性,介质中的流体遵循Biot固结理论和修改的Terzaghi有效应力原理,以最大拉伸强度准则和Mohr Coulomb准则作为损伤阀值对单元进行损伤判断,能同时考虑岩石损伤前后对渗透率的影响,可以对渗透性不均匀岩石水力压裂过程中裂纹的演化行为进行模拟。
数值模型的几何尺寸为400 mm×400 mm,整个模型划分为220×220=48 400个单元;在过模型中心的水平线上开挖两个小孔,孔径为30 mm;模型边界上作用有最大和最小水平应力,水平应力差系数定义为Kn=(σH-σh)/σh;模型中初始孔隙水力压为20 MPa,水压力作用于小孔的内边缘,井孔增压速率为0.5 MPa/步,直至裂纹扩展引起试样的宏观破坏。建立这样的数值模型综合考虑了天然应场水平应力差异系数、岩石非均质性、井孔间距、井孔增加速率等因素对stress shadow效应和临界间距的影响,模型输入参数见表1。
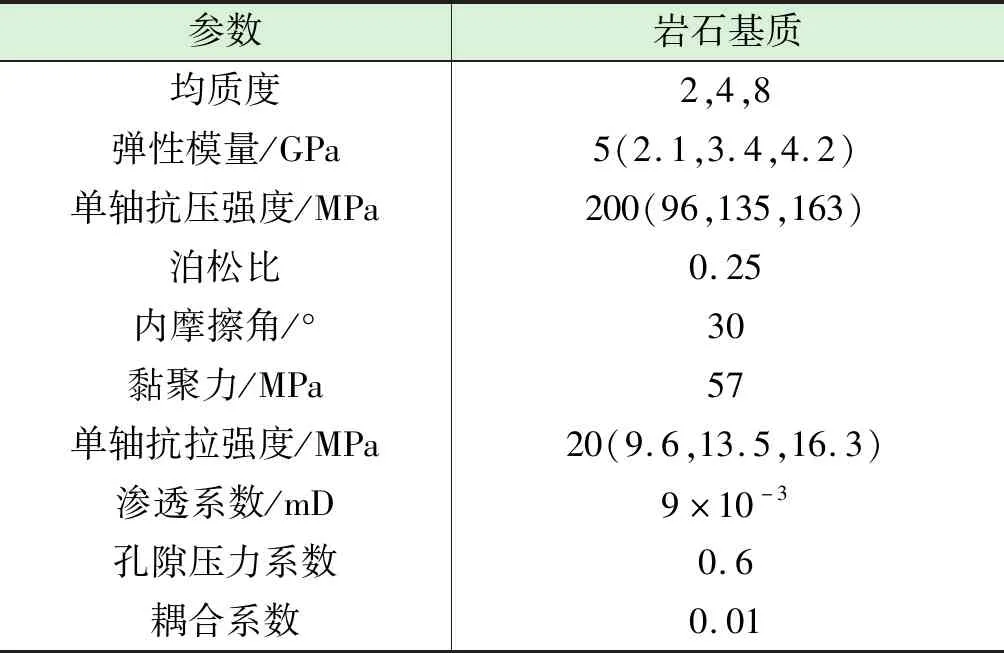
表1 计算模型输入参数
注:强度参数括号中数值为岩石材料的宏观取值。
RFPA-Flow软件采用Weibull分布来表征材料的非均质性,假定组成材料的细观单元的力学性质满足Weibull分布,两参数的分布函数为[15]:
(1)
密度函数为:
(2)
式中:u—岩石介质基元体力学性质参数(强度、弹性模量等),MPa;u0—基元力学性质平均值;m—Weibull分布的形状参数,反映了Weibull分布密度函数的形状,它是反映岩石均质性的一个指标,也称其为均质性系数。
当m>1时,指岩石材料为硬非均质性,代表材料小变形情形;m<1时,指岩石材料为软非均质性,代表材料大变形情形。本文将u0和m称为材料的Weibull分布参数,对于材料的每个力学参数都必须在给定的Weibull分布参数条件下按式(2)给定的随机分布赋值。当u0取定值,形状参数取不同值时,Weibull分布密度函数的曲线见图1。如何将岩石的细观参数与宏观参数联系起来是取得可靠性计算结果的关键,细观强度均质度细度m是数值计算中的重要参数,该参数的确定可考虑两种方法:参考细观单元细观与宏观力学参数的计算式(3)和式(4)以及细观单元数目与脆性指数的关系[15]。
(3)
(4)
式中:Es0、fcs0—细观单元服从Weibull分布时弹性模量和强度的均值;Es、fcs—分别为数值试样宏观的弹性模量和强度,MPa。
以上关系是假定材料的弹性模量和强度的均质度相同,分别服从两个独立的Weibull分布条件下得出的,这与实际情况是相吻合的。
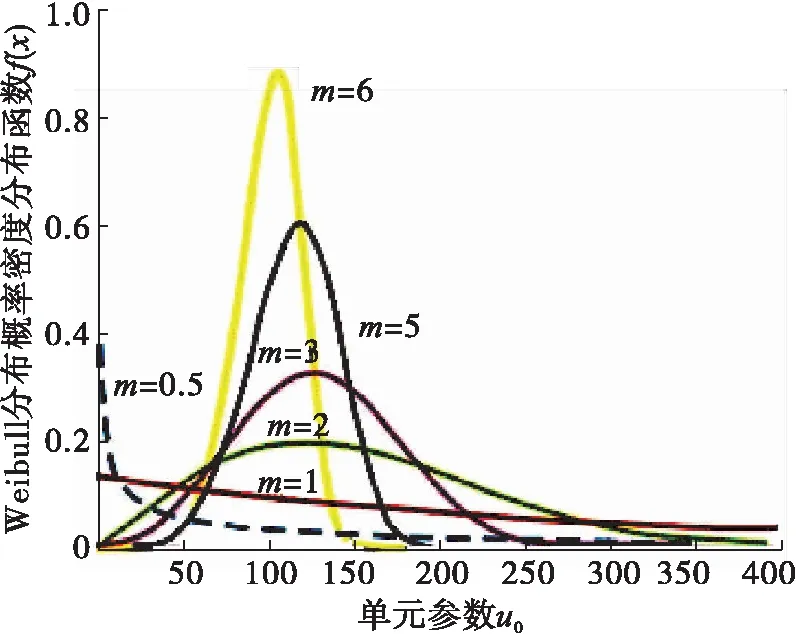
图1 不同m值时单元强度分布
本文对三种不同均质度岩石水力压裂过程中的stress shadow效应进行研究,模型参数见表1。在研究中设计两条横向裂缝布置于同一水平井的情况,综合考虑岩石的非均质性、孔间距和增加速率对stress shadow效应的响应,以确定最佳的裂缝间距。
二、结果与讨论
1. 最小裂缝间距的确定方法探讨
目前,有关水平井多裂缝间距的研究多采用有限元进行模拟,两个相邻裂纹最小裂纹间距的确定对应于应力场倒转90°时的距离,即S90。在S90影响区域内部不会有水力裂纹的出现。在应力反转区域,最大水平主应力平行于水平井方向,导致后来的裂纹或者沿水平井纵向扩展或者由于裂纹方向的改变而砂堵。如果间距超过S90,再次压裂时的水力裂纹仍然受先前裂纹的影响,裂纹间距需要增大裂纹转向的5°或10°距离,超过这个距离,裂纹间距将不再相互作用,S5或S10代表了最小的间距,对于超低渗的页岩储层,在降低裂纹间距的同时也应该保证横向裂缝充分扩展,从而使产能最大化,认为裂缝最小间距为S5(即裂缝转向超过5°的长度)。
2. 岩石非均质性对裂纹相互作用的影响
研究中考虑岩石的均质度系数m分别为2、4和8三种情形。为了更好地反映stress shadow效应对临界间距的影响,设计模型为弱各性异性的情形,模型中水平应力差系数为0.2,以便可以同时考虑井孔间裂纹萌生和平行于大主应力方向裂纹演化的可能性,分析stress shadow效应的作用机制与孔间距的关系以确定最佳临界间距。当井孔间距离分别为50 mm, 130 mm和160 mm时,不同均质度数值模型中水力裂纹相互作用过程见图2。
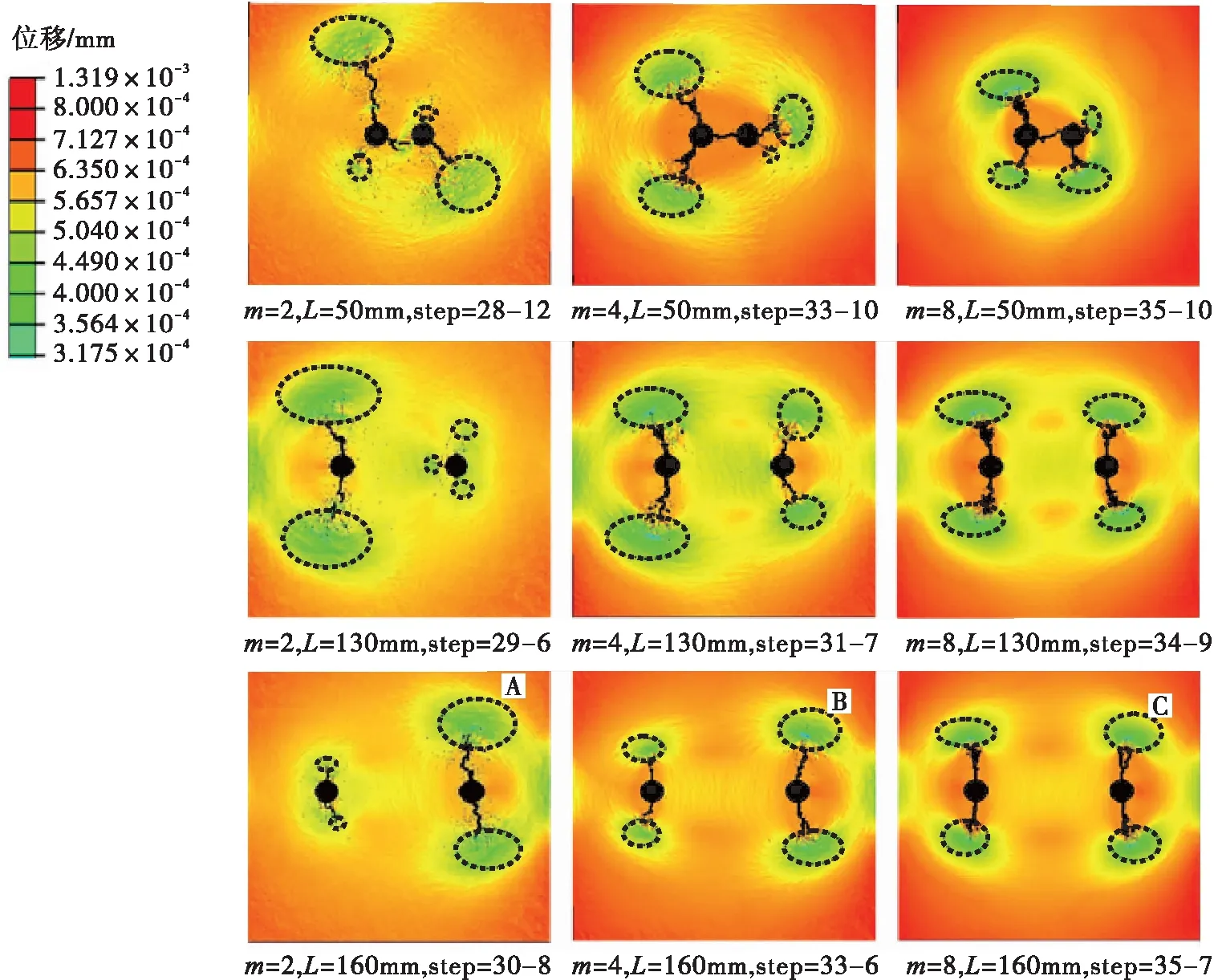
图2 岩石均质度系数m取2,4和8时水力压裂计算结果(Kn=0.2)
根据图2中不同均质度模型,井孔间距取不同值时,裂纹的扩展形态特征为:
(1)L=50 mm时,孔间受stress shadow影响,水力裂纹相互吸引。不同均质度的模型,孔间水力裂纹均相互贯通。双孔上下两侧裂纹相互排斥,由于岩石非均质性原因,上下两侧裂纹不对称,左上和右下裂纹扩展速度较快,抑制了其相邻裂纹的扩展。
(2)L=130 mm,孔间裂纹的stress shadow效应几乎消失,仅非均质性最差的模型(m=2)右孔左侧有一小长度较小的水力裂纹。双孔内水力裂纹沿竖直方向传播,受尖端stress shadow效应的影响,裂纹偏离直线方向发展,各自向外侧扩展。
(3)L=160 mm,孔间不存在stress shadow效应,完全没有裂纹出现。竖直裂纹的传播占优势,上下两侧裂纹尖端在stress shadow效应影响下相互排斥(m=2和4)或抑制,裂纹尖端stress shadow效应对上下两侧裂纹的偏移逐渐减弱。
图3为不同注入速度对临界间距的影响。考虑井孔增压幅度分别为Δp=0.2 MPa,0.5 MPa和1 MPa三种情形。从图3看出,降低注入速率,裂纹间的连通率增强,导致临界距离与实际值之比nx值的增大,较低的水压持续注入井孔处,造成水力裂纹的萌生时间要长于较高水压的情形,在裂纹萌生前孔隙水压向岩石扩散的距离要更长,使应力场的松弛长度更大,促进注入点间的应力场相互作用更强。
由于计算模型中的强度参数(弹性模量和单轴抗压强度)服从Weibull分布,每一次生成的模型参数分布是随机的,为了探讨参数随机分布特性对井孔间距的影响,在均质度系数分别为2、4和8的情况下,对同一井孔间距分别模拟5次。井孔有裂纹萌生时的计算次数与井孔间距的关系见图4。结果表明,模型的非均质性越强,井孔间萌生水力裂纹的可能性越大。为了避免水平井相邻射孔中间有裂纹生成,射孔间距应当增大,然而,增大间距会导致水平井产能下降低。为此,研究储层岩石的非均质性,根据储层自身的特性确定井孔间距是很有必要的。

图3 注入速度对孔临界间距的影响
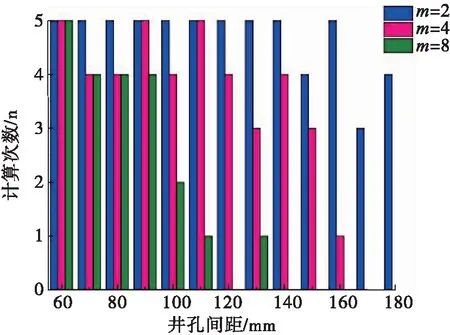
图4 井孔间裂纹萌生的计算次数直方图
三、结论与建议
(1)为了避免径向裂纹的产生,最小的井孔间距为S90。为此,本文在S90(S5)定义的基础上,认为只有当井孔间没有裂纹萌生时的间距为最佳射孔间距,这样可完全避免裂纹裂沿水平井纵向扩展,也不会造成砂堵。有限元法无法实现,然而借助RFPA-Flow程序,综合考虑岩石破裂过程中的应力-渗流-损伤特性可很好地对临界间距进行预测。
(2)当井孔间距小于某临界长度时,井孔间的相互作用较强,容易形成孔间连通的水力裂纹。由stress shadow效应影响的井孔临界间距受岩石的非均质的影响,当岩石的非均质性较强时,影响间距较大。
(3)由于stress shadow效应的影响,水平井射孔间距的确定同样应考虑应力伞的演化特性,伴随着裂纹的动态扩展而不断变化,裂纹尖端的应力伞面积和缝长具有很强相关性,二者服从幂函数分布。

