基于多尺度模型的单层球面网壳结构静力稳定性分析

姜明龙, 朱南海, 陈大龙

(江西理工大学建筑与测绘工程学院,赣州 341000)

空间结构作为新兴的建筑结构,其优势相对突出:整体性能好、材料强度利用率高且材料可充分回收、施工周期短、抗震性能好、造型美观大方、形式丰富多样等。在大跨度空间结构中,网壳结构由于兼具良好的杆件受力性能和壳体的优美形态,成为当今新式建筑中应用最为广泛的结构形式之一。

传统的网壳结构稳定性分析是基于线性方法,其计算结果和实验值有较大出入,随着理论研究的不断深入,不同的计算方法相继被提出,主要有拟壳法[1]、大规模参数分析方法[2]和非线性有限元分析方法[3-4]。多尺度有限元分析方法由于其在计算精度和计算效率两方面均具有较好的平衡,逐渐被国内研究人员推广运用。石永久等[5]深入探讨了多尺度方法在钢框架抗震计算上的适用性问题。陈宇等[6]通过对钢筋混凝土柱拟静力试验和单调推覆数值试验的模拟与对比分析,验证了多尺度方法的适用性。肖祥等[7]提出了建立大跨度桥梁多尺度基准有限元模型的方法和多尺度有限元模型修正方法,通过与实测数据比较分析,验证了该多尺度基准有限元模型的合理性。方钊等[8]研究了钢结构风致疲劳分析中的多尺度有限元建模技术并验证其合理性。李万润等[9]提出了一种考虑隔震支座特性的隔震结构多尺度模拟方法并结合串联隔震结构振动台试验对多尺度分析方法的有效性进一步验证。魏建鹏等[10]以两个单层空间网格结构的典型子结构拟静力试验结果作为校验,探讨了多尺度有限元模型在空间网格结构抗连续倒塌分析中的应用。

传统的全梁单元建模在模拟结构的整体变形和破坏倒塌方面具有较好的表现,但受限于单元划分的密度以及粗糙的节点刚接处理形式,难以有效地模拟网壳薄弱节点以及局部构件的力学响应,进而得到的分析结果存在不可忽略的偏差。此外,网壳结构杆件众多,结构复杂,若采用全实体单元的精细化模型,其庞大的计算量将使得迭代计算的收敛和正确性难以保证,计算代价也较为巨大。

基于上述因素,建立一个充分考虑薄弱节点和薄弱构件变形且单元划分更为细致的精细化模型,以此进行更为精确的结构稳定性分析,尤为必要。模型精细化程度决定计算效率,提高计算效率的关键在于建立合适的多尺度模型。结合近年来多尺度建模方法的研究现状,在对网壳结构进行较为系统的弹塑性稳定性参数分析之后,以平衡计算代价和计算精度为目标,引入多尺度方法[11-12],分别建立薄弱区域节点细化及杆件细化的多尺度模型进行分析与对比,比较两者对模拟结果影响程度大小,为建立在计算精度和计算效率之间取得更好平衡的多尺度模型提供理论基础,以期进一步完善多尺度研究方法在网壳结构受力性能分析中的应用,也为进一步丰富网壳结构的设计和工程实践理论体系。

1 结构多尺度分析基本原理

多尺度方法最早由Hou等[13]基于Ivo等[14]的工作基础提出并推广运用于二阶椭圆边界值问题中,是一种在计算精度及计算代价之间寻找平衡的方法,其主要思想是在宏观单元上应用数值方法构造基函数,由基函数连接宏观和细观单元,将细观单元上的微观非均质信息传递至宏观单元上,因此只需在宏观单元上便能求解原问题,具有精简计算量和缩短计算时间的优点。而且,结构整体线弹性响应及薄弱部位的塑性损伤特征在多尺度模型中得到有效的反馈,在准确还原结构整体响应的同时,能够跟踪薄弱部位的损伤演化全过程。

在多尺度建模过程中,实现跨尺度的连接至关重要。不同尺度界面连接问题主要包含以下3类:梁单元与壳单元连接、梁单元与实体单元连接、壳单元与实体单元连接[15]。采用多点约束(multi-point constraints,MPC)法实现网壳结构模型中梁单元与壳单元的连接,如图1所示。

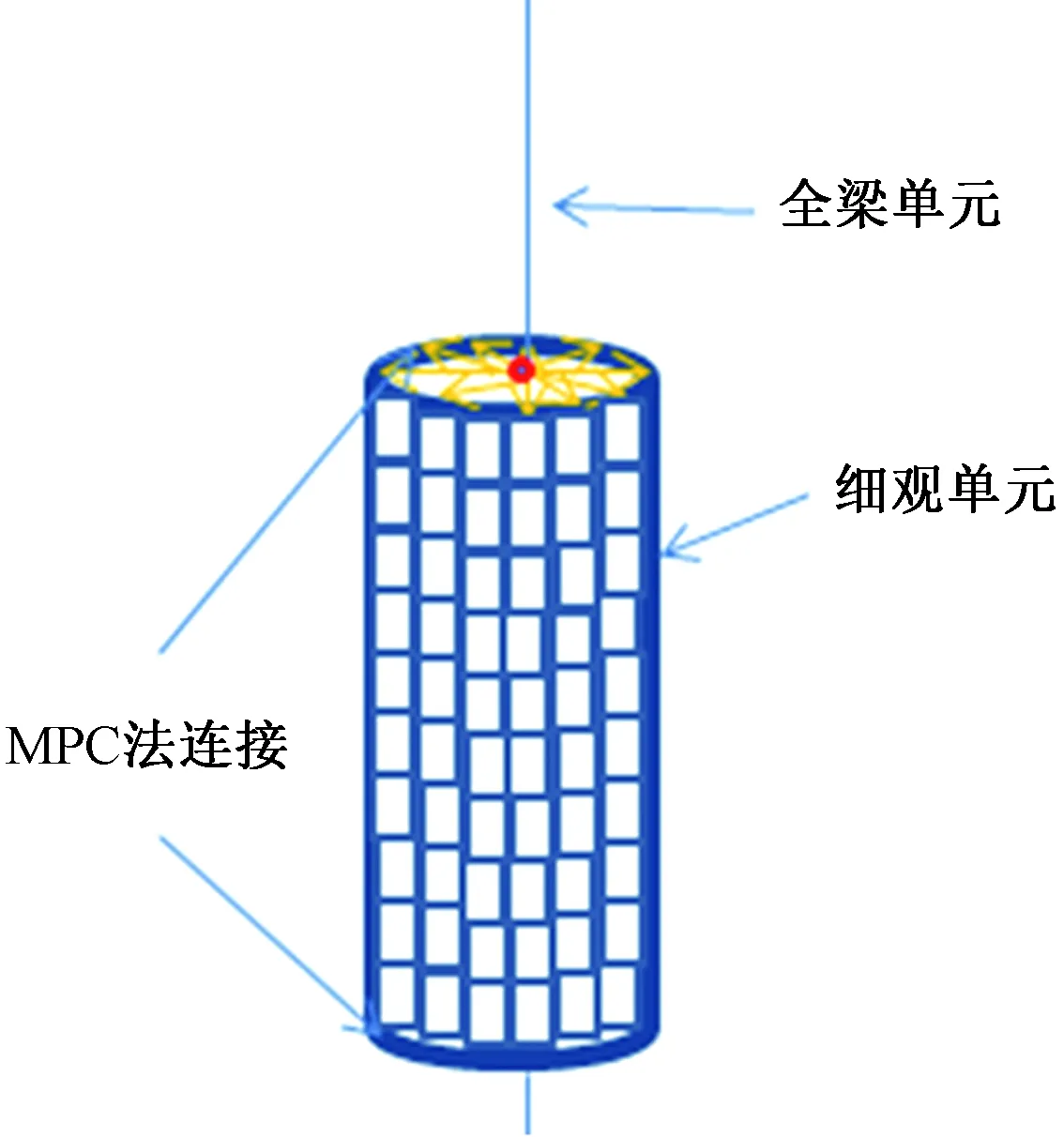
图1 结构多尺度模型示意图Fig.1 Schematic diagram of structural multi-scale modeling

在跨尺度的交界面上,通过节点的位移约束方程将不同尺度单元节点进行连接,进而达到位移协调。采用的约束方程为

(1)

式(1)中:Ub和Ur(i)分别为全梁单元和细观单元节点自由度的数目；N为节点总数；C(i)为连接界面上节点i的相应约束系数。

2 基于多尺度模型的网壳结构静力稳定性分析

如图2所示,网壳结构跨度为60 m,矢跨比为1/5,初始缺陷取L/300(L为结构计算模型的跨度，m),杆件截面采用φ160.0 mm×4.0 mm,质量密度取为7 850 kg/m3,钢材弹性模量E取2.1×105MPa,泊松比ν取 0.3,模型共划分为1 440个单元和1 225个节点。采用两段式的理想弹塑性本构,屈服准则满足Von Mises准则,屈服强度fy为345 MPa,结构支撑条件为周边固定支撑形式,所施加的竖向极限荷载由静力屈曲分析所得。建立结构模型,考虑材料非线性分析和几何非线性分析,对结构的稳定性进行分析。

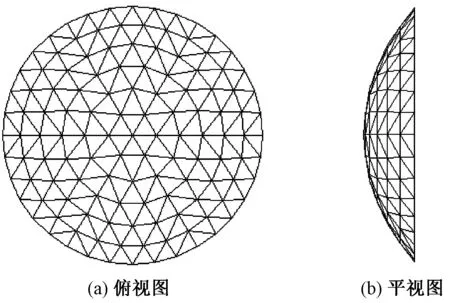
图2 结构计算模型示意图Fig.2 Schematic diagram of structural calculation model

2.1 结构薄弱区域分析

基于全梁单元的模拟结果,直观地确定该类结构在进行稳定性计算时的薄弱区域,采用全梁单元模型进行静力稳定性计算所得结构应力、等效塑性、位移结果如图3～图5所示。

图3 全梁单元模型的应力分布Fig.3 Stress distribution of the full beam element model

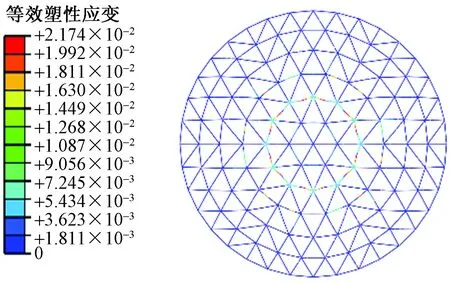
图4 全梁单元模型的塑性分布Fig.4 Plastic distribution of the full beam element model

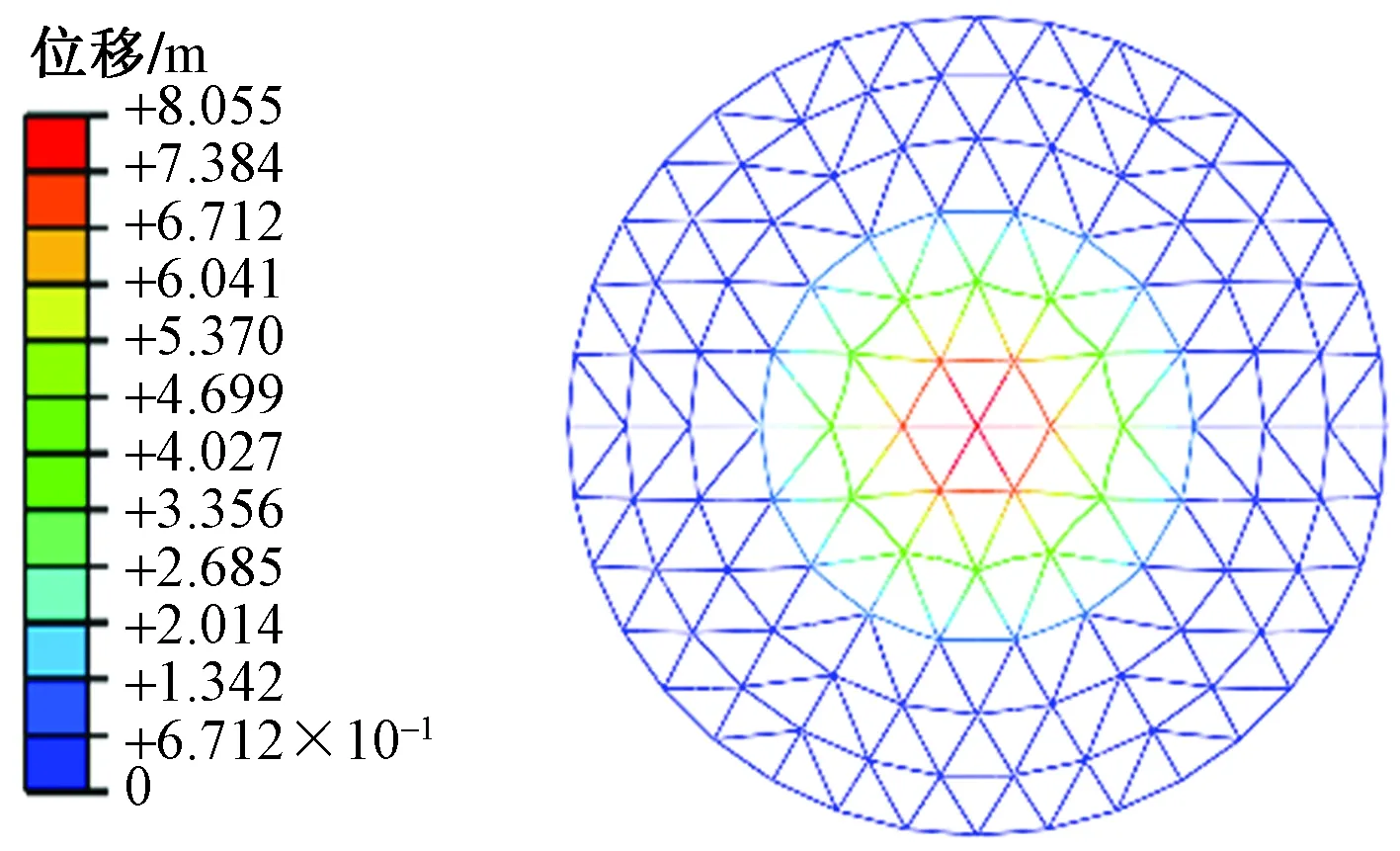
图5 全梁单元模型的位移分布Fig.5 Displacement distribution of the full beam element model

通过观察图3、图4可知,进入塑性的杆件主要集中在第2圈和第3圈的环杆,其中第2圈环杆塑性程度最为严重,第2、第3圈的环杆及第3、第4圈的斜杆出现应力集中现象,第3圈斜杆与第2圈环杆的交接节点处应力集中较为显著。由图5可知,位移形变量最大的区域集中于顶部节点附近。底部杆件仍基本处于弹性阶段,其应力、位移响应值极不明显。可知,顶部区域是结构响应的主要区域,即薄弱区域。在进行双重非线性静力稳定性分析时,应对薄弱区域进行精细化分析。

2.2 薄弱区域节点细化的多尺度模拟

根据全梁单元模型的计算结果,以应力、塑性和位移这3个结构力学性能响应的分布情况来确定结构薄弱区域,选取该区域具有代表性的节点作为重要节点,对其进行精细化建模,采用壳单元类型,应用MPC法来实现跨尺度界面间节点的连接,以此展开结构静力整体稳定性能的多尺度分析。其中,节点细化的多尺度模型几何尺寸、材料参数与全梁单元模型相同,模型共划分为16 472个单元和16 483个节点,选取该结构的第2圈环杆上部分应力集中较为明显的节点进行壳单元细化处理,薄弱节点采用空心球节点类型,与节点相连的杆件交于球心。由《空间网格结构技术规程》(JGJ 7—2010)[16]中规定,空心球壁厚与主钢管的壁厚之比宜取1.5～2.0,空心球外径与主钢管外径之比宜取2.4～3.0,取空心球节点参数为400.0 mm×8.0 mm,球节点与杆件相接处取长度为0.9D(D为杆件外径)[17]的杆段进行精细化处理,其余区域均采用梁单元建模,建立的多尺度模型及节点大样如图6、图7所示。

图6 考虑节点细化的多尺度模型Fig.6 Multi-scale model considering joint refinement

图7 节点处跨尺度连接界面Fig.7 Cross-scale connection interface at joint

参照全梁单元,对多尺度模型进行结构双重非线性稳定性能分析。通过ABAQUS模拟计算,可得相应结构的应力、位移云分布情况如图8、图9所示,其中放大区域为响应最大值出现位置。

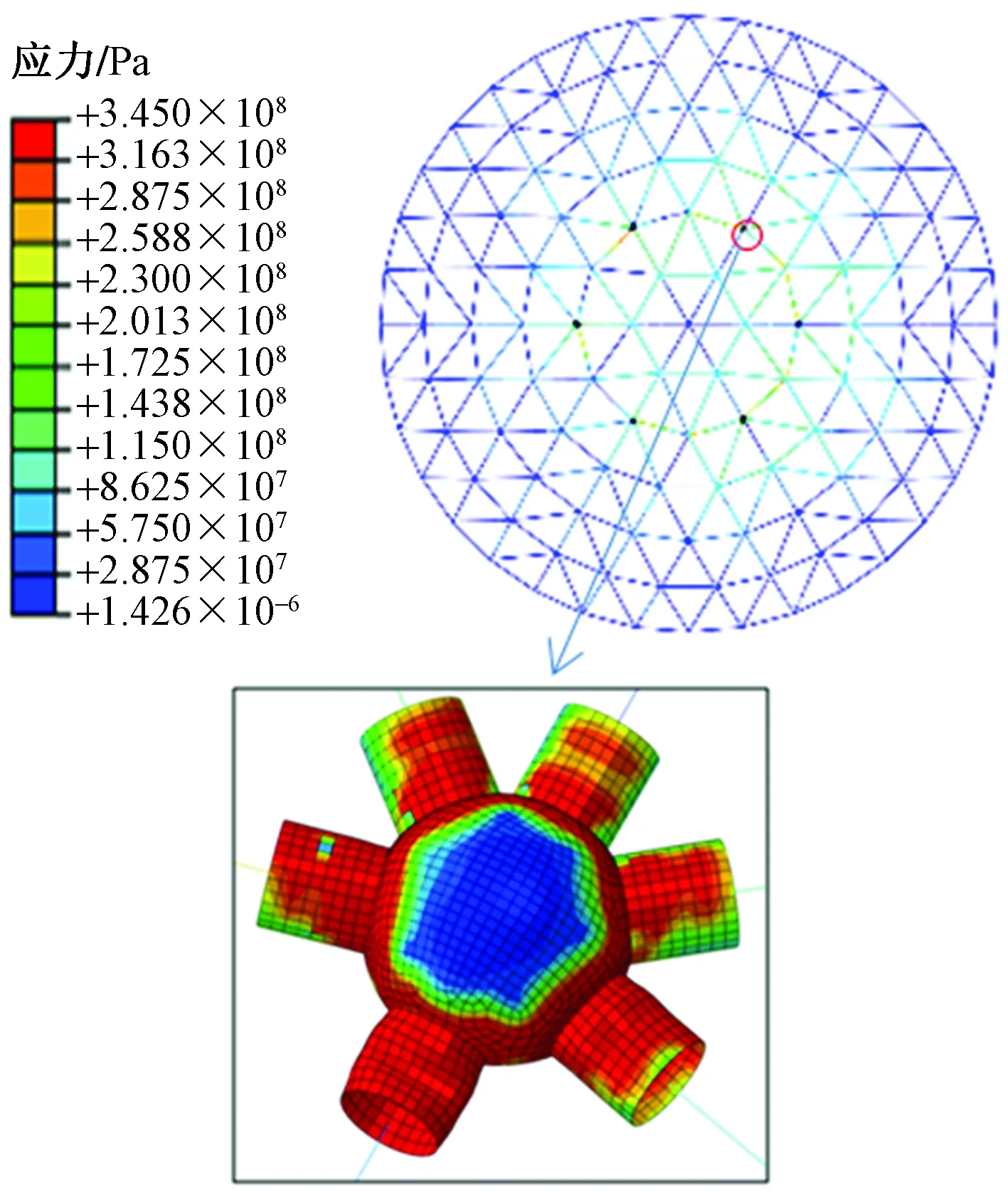
图8 薄弱区域节点细化模型的应力分布Fig.8 Stress distribution of weak area joint refinement model

图9 薄弱区域节点细化模型的位移分布Fig.9 Displacement distribution of weak area joint refinement model

相较全梁单元模型的模拟结果,节点细化多尺度模型中各杆件在静力作用下的响应灵敏度,如杆件塑性屈服程度、应力响应和应变响应均呈现不同程度下降,其中应变响应下降幅度较大。多尺度模型表现出明显的软化过程,产生明显形变,与焊接球相连的部分细化杆件段发生明显变形,局部出现凹陷。但是两种尺度模型仍有许多相似之处,两者在极限荷载作用下的结构最大应力相同,两者共同的主要敏感区域出现在结构顶部,处在底部区域的节点和杆件基本上仍处于弹性阶段,由此,可知该多尺度模型的数值模拟结果具有一定的可靠性。

分析模拟结果可知,其存在差异的原因如下:在全梁单元模型建立过程中,节点和杆件未进行区分处理,两者采用统一设置,未对模型中节点的形状进行设置,而采取粗糙连接的形式,忽略了节点局部变形,使得模拟结果精度较低。结构失稳过程伴随着节点的形状改变和结构的应力重分布,但全梁单元模型所采用的节点刚接形式忽略了其变形,不同于多尺度模型,在网壳结构失稳过程中,多尺度模型节点发生变形软化,分担部分应力和结构变形,减小杆件受力。由图8可知,薄弱节点细化建模方法对结构应力响应的影响不明显,该建模方法具有一定的有效性。此外,因球节点处有较多连接面,受力较为复杂,虽采用节点细化的建模分析方法在研究节点局部变形和局部应力分布方面具有一定的优势,但较多不同类型单元耦合并协同计算,将对结构在静力作用下整体响应的计算精度造成不小影响。

2.3 薄弱区域杆件细化的多尺度模拟

参照全梁单元的位移分布图,根据薄弱区域选取位移明显的杆件进行细化处理,杆件的几何尺寸以及材料同上一节,建立薄弱区域杆件细化多尺度模型,共划分为15 360个单元和15 456个节点,如图10所示。

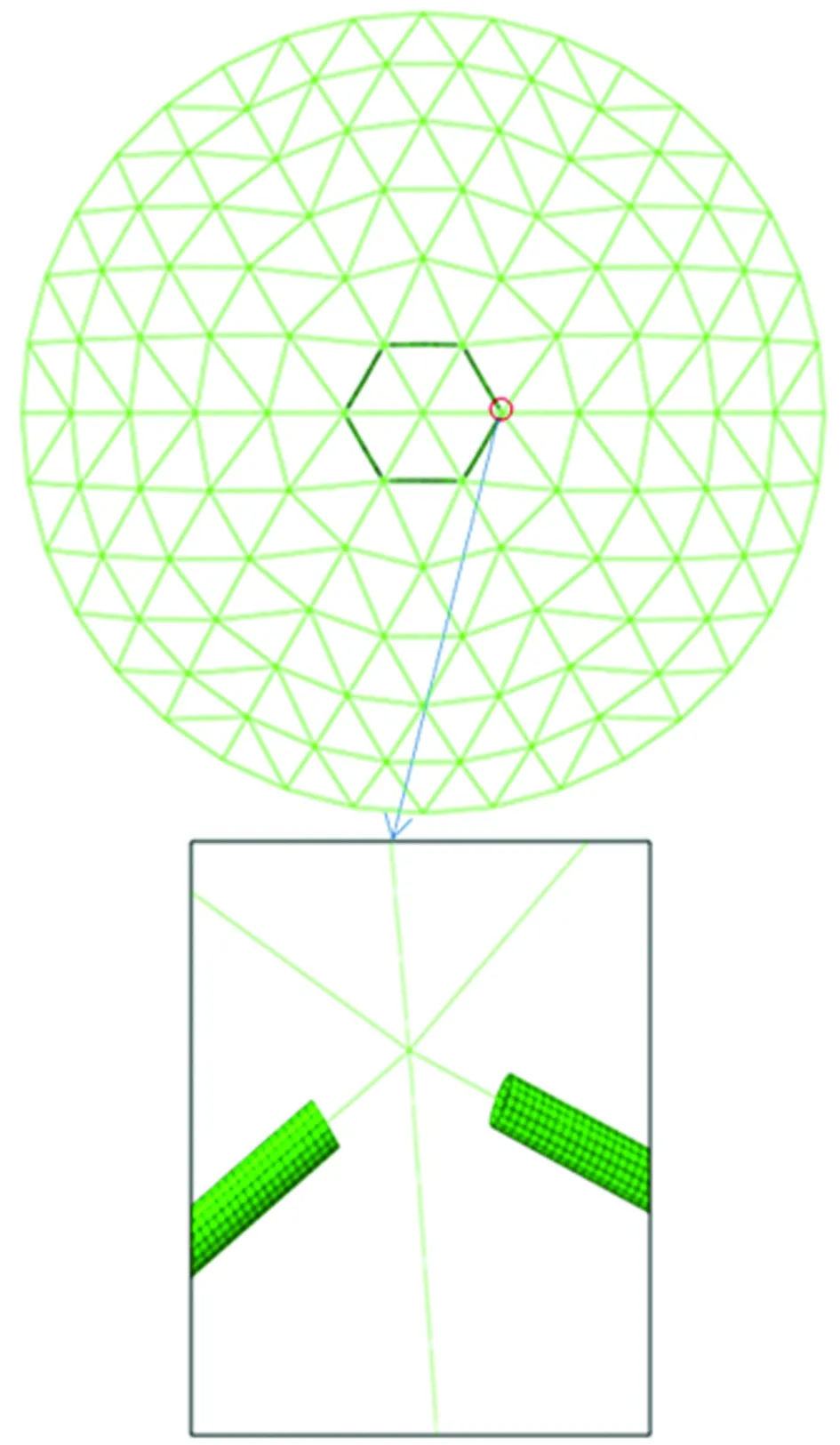
图10 考虑杆件细化的多尺度模型及杆件大样Fig.10 Multi-scale model considering rod refinement and rod sample drawing

参照前文进行结构双重非线性稳定性能分析,根据ABAQUS模拟计算获得结构整体及局部的力学响应分布状况如图11、图12所示,其中放大区域为响应最大值出现位置。

图11 薄弱区域杆件细化模型的应力分布Fig.11 Stress distribution of weak arearod refinement model

图12 薄弱区域杆件细化模型的位移分布Fig.12 Displacement distribution of weak area rod refinement model

由图11、图12可知,与薄弱区域的节点细化结果相比,杆件细化多尺度模型结构整体应力相对均匀,结构最大位移相差不大,但存在局部应力较大现象,最大应力和最大位移均出现在细化杆件上,杆件出现凹陷,发生严重变形。相比全梁单元模型,两者结构位移响应均集中于结构顶部区域,但杆件细化模型在研究薄弱杆件损伤演化方面优势明显,在获得结构整体力学响应特征的同时,跟踪薄弱杆件的塑性发展过程,为探究结构失稳破坏机理提供有力途径。

为更直观地对比分析上述3种模型的模拟计算结果、结构加载过程和整体刚度的改变趋势,根据3类模型模拟结果,绘制图13所示的荷载-位移曲线。

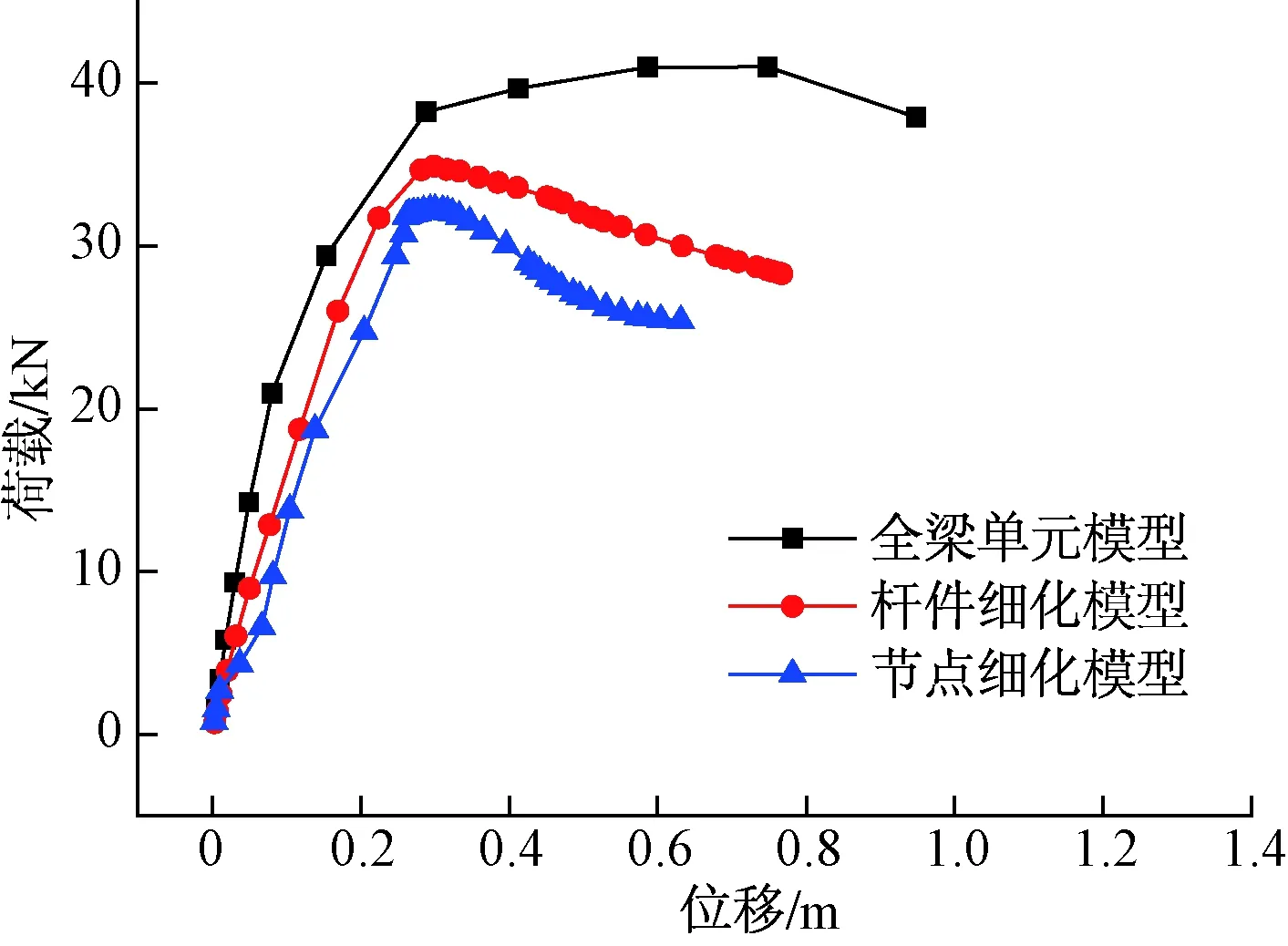
图13 3种建模方法下的荷载-位移曲线Fig.13 Load-displacement curves under three modeling methods

由图13可知,不同数值模拟模型所对应的结构承载力和整体刚度不同。相比之下,基于多尺度建模方法下的模型承载力有较为明显的下降趋势,节点细化的多尺度模型极限承载力下降较为明显,相比全梁单元模型下降约21.4%。对于杆件细化处理的多尺度模型,其结构整体刚度和极限承载力均表现一定的软化和降低,相比全梁单元模型下降14.9%左右。分析原因如下:从模型角度分析,节点细化的多尺度模型设置了详细的球直径和厚度参数,很好地考虑到节点刚度变化以及结构应力重分布,与全梁单元计算模型相比更具适用性,结构模型计算结果更加接近于实际工况。数值模拟过程中,球节点发生一定程度变形,可能导致节点处出现偏心力,进一步改变杆件的力传递路径,结构的极限承载力降低,使得结构未达到全梁单元计算下的极限承载力就发生失稳破坏。整体来看,杆件精细化和球节点精细化的多尺度模型的计算结果相较全梁单元模型而言,更贴近于实际工况,结构承载力计算也具有较高的精度。

通过对3种不同建模方式的模型进行结构静力稳定性分析比较,验证了在大跨度空间结构和网壳结构性能研究中多尺度建模方法的可行性、准确度以及多尺度建模方法在局部细观力学响应分析时的优越性。

3 结论

通过确定结构薄弱区域的方法,采用MPC法实现大跨度空间网壳结构多尺度界面连接,通过建立全梁单元模型、节点细化多尺度模型和杆件细化多尺度模型,分析比较三者在静力荷载作用下的力学响应特征和稳定性,对多尺度建模方法的适用性进行了验证,主要结论如下。

(1)建立了分别考虑节点细化和杆件细化的多尺度模型,相比传统全梁单元模型而言,多尺度模型在计算效率和计算精度之间找到了较好的平衡点,使得在保证模拟计算速度的同时,提高了计算结果的准确度,一定程度上保证了研究结论的质量。

(2)考虑节点细化的多尺度模型和考虑杆件细化的多尺度模型计算结果均显示,相较于全梁单元,结构的极限承载能力和刚度有所降低,其中结点细化的多尺度模型极限承载力下降较为明显,达到21.4%。这反映了考虑薄弱节点受力变形和软化及薄弱杆件受力变形的多尺度模型更加贴近于实际工况。

(3)多尺度模型相较于传统的全梁单元,既能精确地确定薄弱区域节点和杆件的边界条件,也能较为清楚地显示出大跨度空间网壳结构细节部位的塑性发展趋势、破坏过程及失效模式,为大跨度空间结构的设计提供了新的思路,对维修加固等工程提供了一定的参考和依据。