超声面波法在混凝土强度检测中的应用研究

杨道煌，刘江平，程飞，庞凯旋

(1.中国地质大学(武汉) 地球物理与空间信息学院，湖北 武汉 430074；2.中国地质大学(武汉) 海洋学院，湖北 武汉 430074)

0 引言

随着我国经济的快速发展，全国对于城镇规模的建设需求也在不断增大，从而涌现出大量的建设工程。混凝土是公路、桥梁和房屋等建筑工程中最主要的材料，其使用范围非常广泛。在一种情况下混凝土结构体的外层是不同的，因为通常会在其表面覆盖一层其他材料(也可能是强度较低的混凝土)作为保护层或者装饰。而另一种情况是受湿度、温度(特别是在相对低温的情况下)、化学和生物等因素引起表层性质的变化，受损层的厚度可能随时间增加，而且该层通常表现出较低的强度。混凝土强度的降低会引起严重的安全问题，造成重大的人员伤亡和巨大的财产损失，所以需要对混凝土结构体进行强度检测，对存在于混凝土中的安全隐患进行消除。

但是以往的混凝土检测方法均存在一些不足，不能达到很好的效果，在实际应用中受到了阻碍。混凝土抗压强度可以通过抗压试验得到，但是在很多情况下对混凝土进行抗压试验是极其不方便的，且不易操作，实用性较差。抽芯取样法对混凝土质量可进行准确、直观地判断，但是会对原有结构产生一定的破坏。回弹法是20世纪60年代出现的一种混凝土强度检测方法，该方法具有精度高等优点，但是操作不够简便，实用性不强，不能反映混凝土层状介质参数。而瑞利波勘探作为一种工程地质勘探方法[1-2]，在工程地质勘察与检测中得到广泛的应用[3-5]，而且可以利用瑞利波的频散特征[6-7]，反演地下地质结构，获取层状介质的横波速度[8-10]，该方法同样可以应用到混凝土介质中。近些年来，随着声波检测技术的发展[11]，出现了使用瑞利波方法识别混凝土参数的技术[12-14]，也可以在混凝土质量检测中得到应用。

本文利用超声波检测仪得到实测的混凝土面波数据并提取频散曲线[15-16]，通过阻尼最小二乘法和奇异值分解反演算法得到横波速度[17-18]，结合弹性模量法和幂函数拟合法换算出强度值，从而对混凝土强度进行评价。结果表明，使用瑞利波频散曲线进行混凝土强度检测能够达到实际要求，瑞利波方法可以进一步完善混凝土实体质量检测手段，可对混凝土结构物中的安全隐患进行消除，避免了灾害的发生，有力地推动了混凝土工程的发展。

1 瑞利波勘探方法

1.1 反演方法

1.1.1 反演方程的建立

阻尼最小二乘法作为传统的瑞利波线性反演方法的一种，具有方法简单、反演速度快等优点，也是瑞利波处理常用的通过反演相速度估计横波速度的方法。水平层状模型中瑞利波的相速度CRj可以根据公式

Fj(fj,CRj,VS,VP,d,h)=0, (j=1,2,…,m)

(1)

计算。式中：m为数据点的个数；fj为频率；CRj为瑞利波的相速度；VS为S波速度向量；VP为P波速度向量；d为密度向量；h为厚度向量。

横波速度是影响瑞利波相速度的主要因素，而纵波速度和密度的变化对瑞利波相速度的影响十分微弱，故在反演过程中这两个参数作为已知量，减少了反演中的未知量，使反演过程得到简化并提高了反演的稳定性。因此瑞利波频散方程可以表示为如下函数：

CRj=G(VS,fj) 。

(2)

在瑞利波的反演算法中，将横波速度表示为向量x，瑞利波的相速度也可以表示为向量b。将式(2)Taylor级数展开并取一阶近似，线性化后可以得到：

JΔx=Δb，

(3)

式中，J为函数G关于元素VS的一阶偏导数所组成的m行n列(m>n)的雅克比矩阵；Δx为S波速度的修正量；Δb=b-CR(x0)是初始值的模型响应和数据之间的差。

根据Marquardt法，在求解地球物理的线性反演问题时，式(3)中的目标函数应具有方差项和模型长度项两项内容。将目标函数定义如下：

(4)

式中，‖‖2是L2的矢量长度；W是一个加权矩阵，W=LTL，L也是一个对角矩阵。α为阻尼因子。

1.1.2 反演方程的求解

利用Marquardt法将该问题简化为：

(ATA+αI)Δx=g,

(5)

式中，I为单位矩阵；g=ATΔd为n维向量；A=LJ。

利用奇异值分解技术，矩阵A奇异值分解式为：

A=UΛVT。

(6)

利用奇异值分解后可得到横波速度修正值：

Δx=V(Λ2+αI)-1ΛUTd,

(7)

式中：d=Lb，I为单位矩阵。

1.2 混凝土强度计算原理

我国最新标准规定，C60强度以下的混凝土可采用边长为150 mm的立方体试件作为混凝土抗压强度的标准尺寸试件。按照《普通混凝土力学性能试验方法标准》，制作边长为150 mm的立方体，在标准养护(温度20±3℃、相对湿度在90%以上)条件下，养护至28天龄期，用标准试验方法测得的极限抗压强度，称为混凝土标准立方体抗压强度，以fcu,k表示。

1.2.1 弹性模量法

地震纵波和横波在介质中传播的速度与介质的弹性参数之间的定量关系为：

(8)

(9)

式中,λ，μ是拉梅常数；ρ是介质的密度；E是弹性模量；ν是泊松比。

由式(8)和式(9)可以得到同一介质中纵波和横波速度比的关系如下：

(10)

利用式(10)可以计算出介质泊松比，由式(9)可以得到弹性模量的关系式如下：

(11)

根据反演结果可以得到混凝土梁每层的横波速度，根据式(11)就可以计算得出每层的弹性模量，关于弹性模量换算出混凝土强度的问题可由以下公式求解[19]：

(12)

式中：fcu,k是28天龄期立方体抗压强度，MPa；E是混凝土弹性模量，GPa。

1.2.2 幂函数拟合法

为了将瑞利波方法应用于混凝土强度检测中，需要建立混凝土强度与瑞利波相速度之间的关系，经过直线方程、指数方程、抛物线方程和幂函数方程回归分析对比后，已证明使用幂函数拟合的效果最好[20]，得到两者的关系如下：

(13)

式中：RC是混凝土强度，MPa；A、B是相关系数。

按对数线性回归分析得到瑞利波相速度与混凝土强度关系表达式为：

(14)

式中：fcu,k是混凝土强度换算值，MPa；Vr为每层平均瑞利波相速度。

1.2.3 回弹法

回弹法是早期主要的混凝土强度检测技术，在工程质量检测中得到广泛应用。回弹法计算混凝土强度的公式为[21]：

(15)

式中：fcu,k为推定强度，vai为纵波声速，Rai为回弹值。

2 理论模型计算与试验

2.1 理论模型及强度计算

为了验证瑞利波方法用于混凝土强度检测的可行性和有效性，设计了一个两层混凝土梁模型。使用有限差分法对瑞利波进行正演模拟，从模拟的地震记录中提取频散曲线，使用阻尼最小二乘法反演得到介质各层的横波速度和厚度，最后得到的瑞利波频散曲线和横波速度则可以用于计算混凝土强度。该模型的具体参数见表1。瑞利波正演模拟的网格点数为300×2 000，时间采样步长为0.1 μs，震源设置采用主频为20 kHz的雷克子波，边界设置采用自由界面边界条件和完全匹配层吸收边界。

表1 两层混凝土梁模型介质参数Table 1 Medium parameters of two-layer concrete beam model

图1a是两层混凝土梁数值模拟的地震记录，从图中可见，PML吸收边界条件对边界的反射干扰吸收效果较好，其次使用了自由界面边界条件，使层状混凝土梁的瑞利波得到了有效模拟。图1b为对图1a使用相移法提取的频散曲线，黑色的实心点为拾取的频散曲线点。

采用阻尼最小二乘反演算法对理论频散曲线数据进行反演的结果如图2a和2b所示。在横波速度和厚度都是未知的情况下，初始模型总共分为30层，每层厚度均取为1 cm，初始模型中每层的横波速度均相同，横波速度在混凝土介质合理的横波速度范围内随机生成。对图2所示的反演结果可以发现，正演模拟获得的频散曲线与反演获得的频散曲线相吻合，两者之间的相对误差为0.2%，表明采用阻尼最小二乘法反演得到的频散曲线和数值模拟得到的频散曲线能够很好的拟合，反演结果与模型参数相吻合，说明阻尼最小二乘反演算法可以很好地对层状混凝土介质频散曲线进行反演，为混凝土强度的计算奠定了良好的基础。

图3为表1设计的两层混凝土梁模型的强度随厚度的变化，图中的长虚线为幂函数拟合法计算出的混凝土强度值，幂函数拟合法计算获得的强度曲线具有最小值和最大值，分别对应第一层和第二层的强度值，但是两者之间的差值不大。图中的短虚线为弹性模量法计算出的混凝土强度值，从图中可以发现， 两种方法计算得到的混凝土强度值差别较大。图中实线为理论强度值，在第1层弹性模量法计算的强度值与理论强度值之间的误差为1.10%，第2层两者之间的误差为0.77%。在第1层幂函数拟合法计算的强度值与理论强度值之间的误差为49%，第2层两者之间的误差为18.7%，分层情况与正演模型相对应。综上分析，弹性模量法和幂函数拟合法计算混凝土强度是可以实现的，表明瑞利波方法能够应用于评价混凝土强度。幂函数拟合法计算的两层强度值比较接近而且变化范围较小，存在分层特性但不是很明显，且计算的结果误差较大，与弹性模量法相比实用性较差。

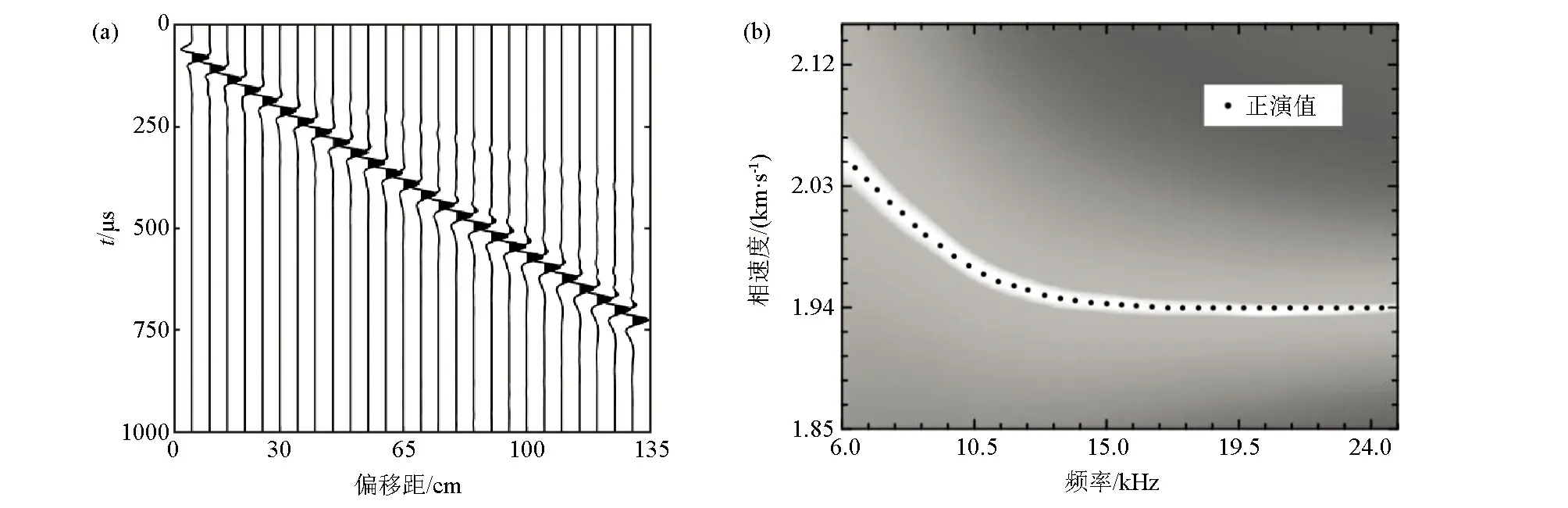
图1 两层混凝土梁模型瑞利波地震记录(a)及频散曲线(b)Fig.1 Rayleigh wave seismic record (a) and dispersion curve (b) of two-layer concrete beam model

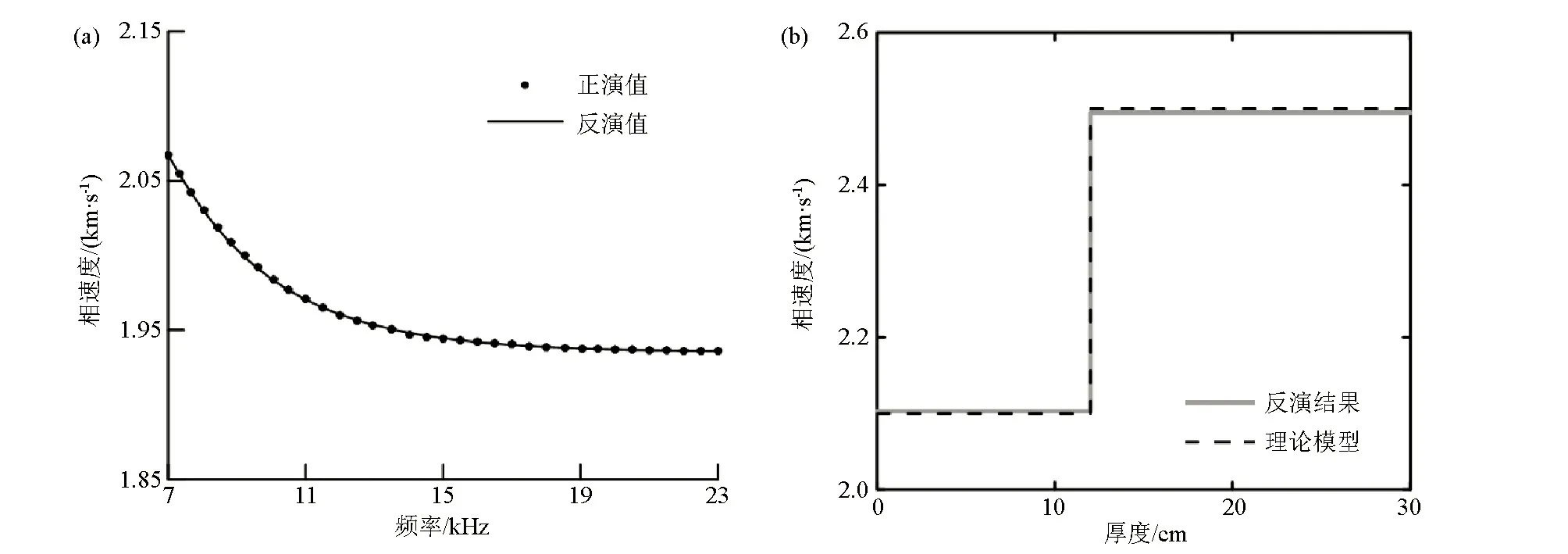
a—频散曲线数值模拟与反演结果的拟合情况;b—横波速度反演结果a—fitting of numerical simulation of dispersion curve and inversion result;b—S-wave velocity inversion results图2 两层混凝土模型阻尼最小二乘算法反演结果Fig.2 Inversion results of damped least squares algorithm for two-layer concrete model

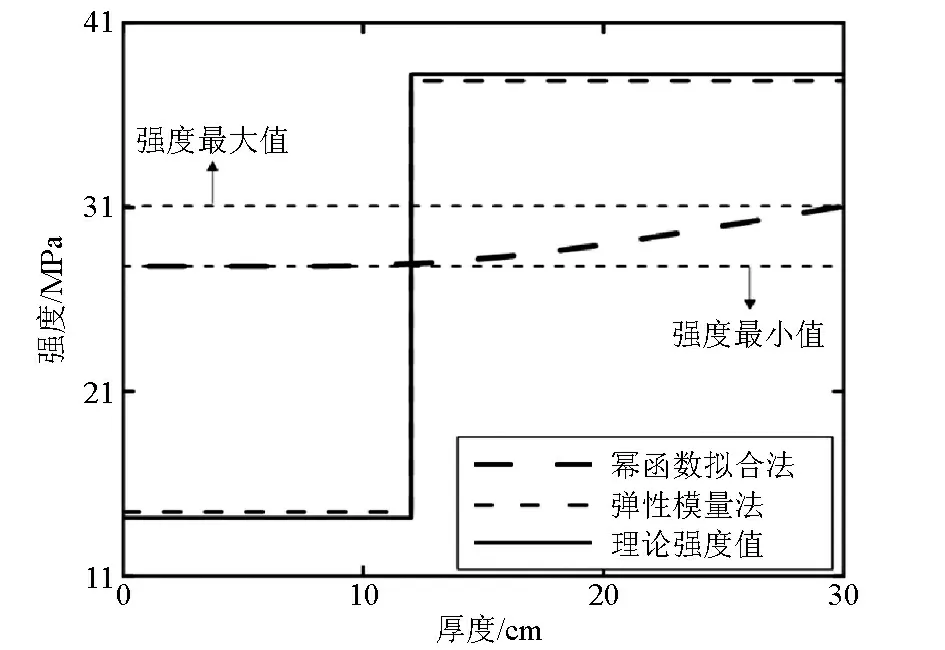
图3 两层混凝土梁模型强度与厚度的关系Fig.3 The relationship between strength and thickness of two-layer concrete beam model

2.2 试验方法

为了将瑞利波方法应用于实际的混凝土强度评价中，将采用上述方法对实际中的混凝土梁进行强度检测，并与传统的回弹法进行比较。实验过程中利用声波检测仪的探头在两个被测混凝土梁表面以一定间隔沿直线剖面移动并得到面波记录(图4)。所使用的超声波探头是一般市场供应的声波仪，其探头均为夹心式(郎之万型的改进型)，它的发射探头主振动方向与换能器轴线平行，但其径向也存在振动，在理论上超声波探头在混凝土表面可以产生瑞雷面波。为了得到完整准确的瑞利波记录，探头与被测混凝土梁之间使用了不影响介质性质的耦合剂。瑞利波数据采集时，接收探头沿第一块混凝土梁(CB1)表面移动26道，在第二块混凝土梁(CB2)表面移动18道，两次实验的道间距均为5 cm，最小偏移距均为5 cm。

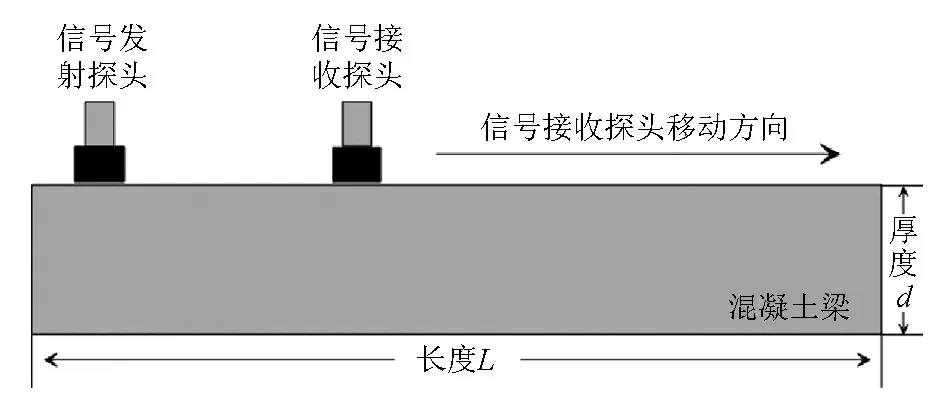
图4 瑞利波数据采集Fig.4 Rayleigh wave data acquisition

图5所示为采集到的混凝土梁瑞利波记录。由于实测对象是处于不同地方的两块混凝土梁，两块混凝土梁介质性质不同，表面的光滑度也不相同，接收探头在混凝土梁上的接触不够紧密或者耦合剂使用不足，导致图5a中的地震记录与图5b相比区别较大，但是不影响瑞利波频散特征的提取和分析。利用称重法可以得到研究对象的密度，应用超声波对测法可以得到研究对象的纵波速度，横波速度和每层厚度则使用阻尼最小二乘法反演得到，通过反演方法得到的横波速度可用于研究混凝土强度。

接收到的面波记录使用相移法处理并得到有效频率范围内的频散曲线，获得的频散曲线如图6中的黑色实心点所示。反演方法采用阻尼最小二乘法，由于纵波速度和密度是已知的，所以反演时只需要反演横波速度和厚度。初始模型总共分为23层，每层厚度均取为1 cm，初始模型中每层的横波速度均相同，横波速度在混凝土介质合理的横波速度范围内随机生成。对反演得到的模型参数进行理论计算可以得到反演结果模型的频散曲线，理论计算方法采用的是快速矢量传递算法。反演后的频散曲线如图7a和图8a中的实线所示，可以发现实测频散曲线与反演频散曲线拟合效果较好，对于CB1两者的相对误差为0.21%，对于CB2两者的相对误差为0.42%。图4显示了横波速度结构以及横波速度平均值，表示了横波速度在层状混凝土梁中的变化情况。图中的Vs1和Vs2分别表示混凝土梁CB1反演结果中的第1层和第2层的平均横波速度，Vs3和Vs4分别表示混凝土梁CB2反演结果中的第1层和第2层的平均横波速度，如图中黑色虚线所示。两块混凝土梁的介质参数如表2所示。反演得到的CB1总厚度为23 cm，反演得到的CB2总厚度为22 cm，结果符合实际情况。从频散曲线的拟合程度和相对误差来看，频散曲线的拟合存在较小的误差，拟合效果较好，误差在可接受范围内，从而可以正确地对强度进行计算和分析。

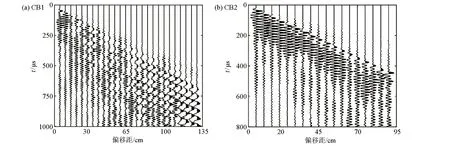
图5 混凝土梁实测瑞利波记录Fig.5 Raleigh wave recording of concrete beam

图6 实测瑞利波频散曲线Fig.6 Measured Rayleigh wave dispersion curve

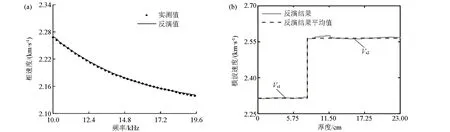
a—实测频散曲线与反演结果的拟合情况;b—横波速度反演结果a—fitting of measured dispersion curve and inversion result;b—S-wave velocity inversion results图7 混凝土梁CB1阻尼最小二乘算法反演结果Fig.7 Inversion results of damped least squares algorithm for concrete beam CB1

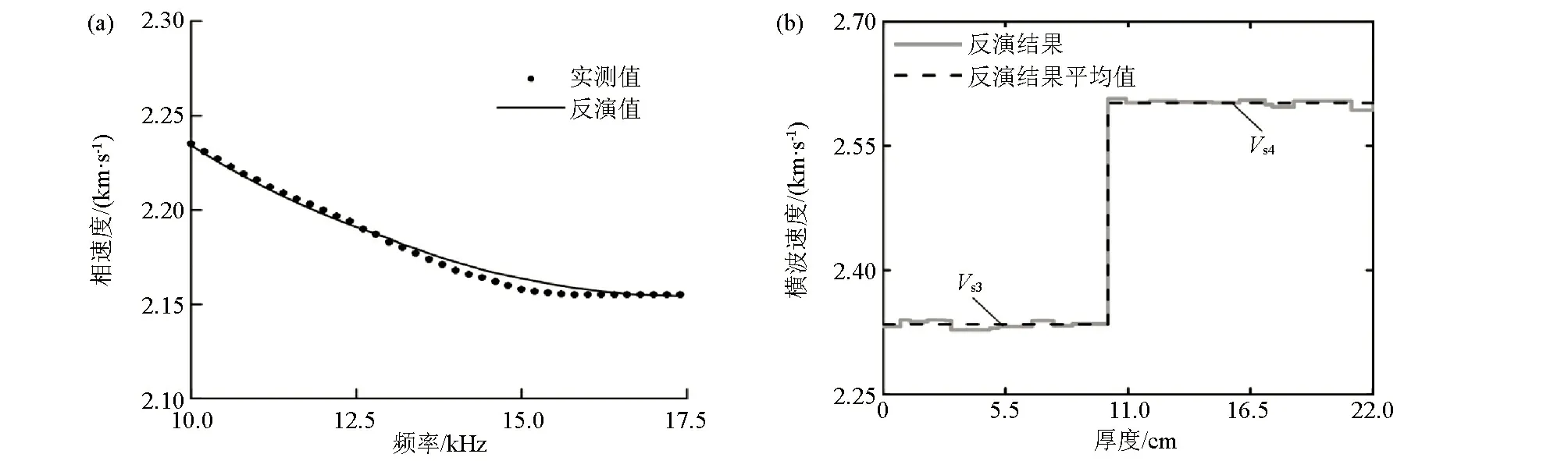
a—实测频散曲线与反演结果的拟合情况;b—横波速度反演结果a—fitting of measured dispersion curve and inversion result;b—S-wave velocity inversion results图8 混凝土梁CB2阻尼最小二乘算法反演结果Fig.8 Inversion results of damped least squares algorithm for concrete beam CB2

表2 混凝土梁反演结果Table 2 Inversion result of concrete beam

3 混凝土强度评价与分析

弹性模量法与纵波速度和横波速度有关，纵波速度可直接测量得到，所需要的横波速度可以利用频散曲线反演得到，根据弹性模量与纵、横波速度的关系进而求出混凝土梁的弹性模量值，弹性模量的大小对混凝土强度有直接影响，弹性模量值也可以评定混凝土的强度等级(图9)。强度等级与弹性模量值以及强度值的关系如表3所示，最后利用弹性模量可以计算出混凝土强度。因此，弹性模量法无法作为一个单独方法来对混凝土结构体进行评价，需要依赖反演方法或其他能获得横波速度的方法。幂函数拟合法是按对数线性回归分析得到的面波相速度与强度的关系式，利用实测的瑞利波相速度，就可以换算出强度值，从而实现对混凝土强度的评价。幂函数拟合法在步骤上省略了反演过程，将频散曲线直接应用到公式中，简化了求取强度的过程，但计算精度并没有得到提高。回弹法作为传统的获取混凝土强度的方法，主要与纵波声速和回弹值有关，利用回弹法可以对上述两种方法进行对比验证。三种方法计算得到的强度值及误差如表4所示。

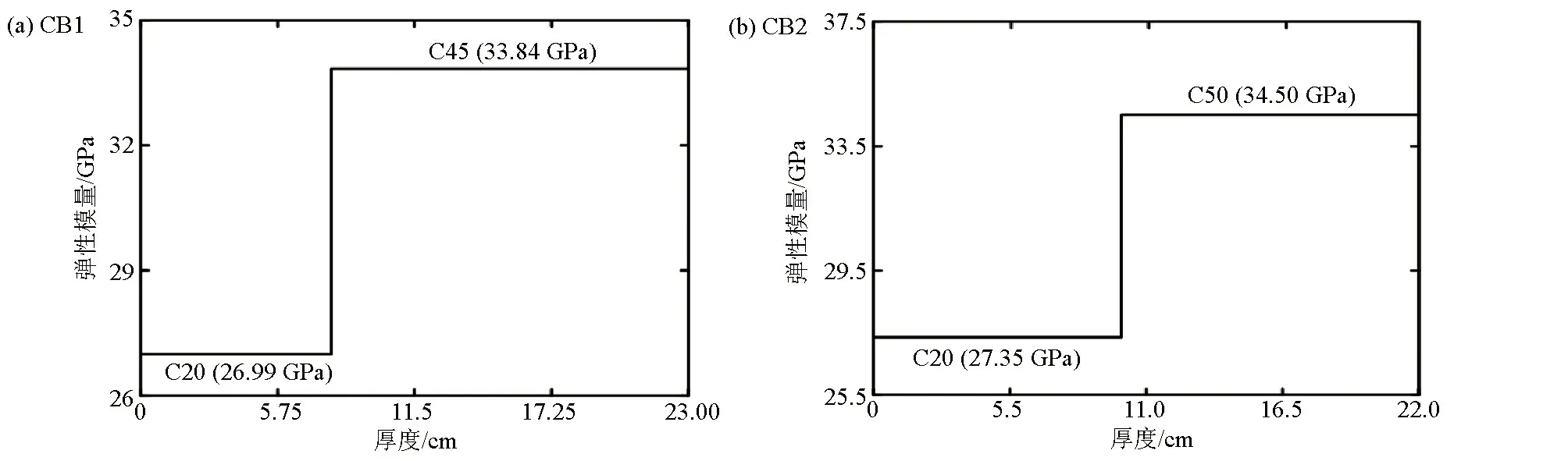
图9 弹性模量与厚度的关系Fig.9 The relationship between elastic modulus and thickness

表3 混凝土强度等级Table 3 Strength grades of concrete

图10表示混凝土梁的抗压强度随层厚的变化，图10中的短虚线为弹性模量法计算出的混凝土强度值，图中的实线为回弹法计算出的混凝土强度值。对于混凝土梁CB1和CB2，第1层的抗压强度比第2层的抗压强度低，其中R1与R2分别代表由回弹仪测量得到的混凝土梁两个不同表面的回弹值。将弹性模量法和回弹法计算出的混凝土抗压强度进行对比，两种方法计算出的抗压强度几乎吻合，对于CB1两种方法计算的强度值，在第1层两者之间的误差为3.79%，在第2层为2.76%，对于CB2两种方法计算的强度值，在第1层两者之间的误差为4.28%，第2层为4.26%。

图11中长虚线和实线分别表示幂函数拟合法和回弹法计算的抗压强度值随层厚的变化。对于CB1两种方法计算的强度值，在第1层两者之间的误差为30.16%，在第2层为19.1%，对于CB2两种方法计算的强度值，第1层两者之间的误差为30.4%，第2层为26.49%。由此可知，使用幂函数拟合法计算混凝土强度的精度比弹性模量法低，弹性模量法的效果较好。弹性模量法对横波速度和纵波速度要求较高，在实测过程中需要得到准确的纵波速度，需要经过严格的反演过程得到横波速度，结合纵波速度和横波速度就可得到较为准确的混凝土强度。幂函数拟合法只与面波相速度有关，所以频散曲线的质量决定了强度计算的准确性。幂函数拟合法强度曲线能直观地表现出强度随厚度的变化而变化，给定混凝土梁强度值的范围，分层情况也与弹性模量法一致，可能由于按对数线性回归分析得到瑞利波相速度与混凝土强度关系表达式不适用于本文中的实测对象，导致幂函数拟合法计算的结果与其余两种方法计算的结果存在一些差异，表明该方法应用范围较窄。

按照规定，普通混凝土划为14个等级，即：C15、C20、C25、C30、C35、C40、C45、C50、C55、C60、C65、C70、C75、C80。例如，强度等级为C25的混凝土是指25 MPa≤fcu,k<30 MPa。试验表明(以弹性模量法为例)，混凝土梁CB1第1层的强度等级为C20，第2层的强度等级为C45；混凝土梁CB2第1层的强度等级为C20，第2层的强度等级为C50。新规范规定混凝土结构体的混凝土强度等级不应低于C15，所以目标混凝土梁满足质量要求。

表4 不同方法的强度值及误差Table 4 Strength values and errors of different methods

图10 弹性模量法和回弹法计算的强度对比Fig.10 Comparison of elastic modulus method and rebound method

图11 幂函数拟合法和回弹法计算的强度对比Fig.11 Comparison of power function fitting method and rebound method

4 结论

在本文的研究中，使用超声波检测仪得到面波数据，获得目标混凝土梁的面波频散曲线，采用阻尼最小二乘法对混凝土结构体的面波频散曲线进行反演，有效地获得了混凝土梁的横波速度结构，结合弹性模量法和幂函数拟合法，并且与传统的回弹法进行比较分析，实现对混凝土强度的评价。得到的结果表明：

1)通过阻尼最小二乘反演算法对混凝土梁的频散曲线进行拟合，反演结果较好，并得到了准确有效的横波速度结构，采用超声面波法可有效获得混凝土梁横波速度结构，进而能准确地求取混凝土抗压强度，可以为后续的混凝土强度评价提供准确有效的初始条件。

2)弹性模量法和幂函数拟合法作为混凝土强度评价的方法均能得到目标混凝土结构体的强度值，经过与回弹法的对比验证，弹性模量法计算得到的强度值与回弹法得到的强度值基本一致，均能得到较准确的结果，且能够达到实际精度要求，而幂函数拟合法计算得到的结果与其余两种方法相比差异较大。与幂函数拟合法相比，弹性模量法需要明确混凝土结构体的横波速度、纵波速度和密度，而在一般情况下横波速度是很难直接得到的，所以需要利用反演方法或者其他方法获取横波速度，而幂函数拟合法只与频散曲线相速度有关，参数要求较少且减少了反演过程。弹性模量法在理论上多做了一些工作，也得到了更加准确的结果，幂函数拟合法虽然简便易实现，但是得到的结果不准确，也表明幂函数拟合法实用性不强。在实际应用中，与回弹法相比弹性模量法更方便实用，并且能获得混凝土结构体的内部分层情况。

3)试验表明，利用瑞利波检测混凝土结构体强度是可行且有效的，使用瑞利波方法进行混凝土强度检测能够达到实际要求，可以进一步完善混凝土实体质量检测手段，可对混凝土结构物中的安全隐患进行消除，也可以是以后混凝土质量检测的发展方向。