基于圈复杂度的阶段动态符号执行*

毕雪洁，於家伟，李世明,2

(1.哈尔滨师范大学 计算机科学与信息工程学院，黑龙江 哈尔滨 150025；2.上海市信息安全综合管理技术研究重点实验室，上海 200240)

0 引言

路径爆炸问题降低了软件测试的效率和质量，也给软件埋下隐患。如何缓解路径爆炸问题成为软件安全测试中的一个研究热点，符号执行[1]成为缓解该问题严重程度的重要技术之一。其主要算法思想为利用符号变量来取代测试过程的真实用例，从而在执行过程中获取对应的执行路径，成为生成高覆盖测试用例和在复杂软件应用程序中查找深度错误的有效技术之一；因该技术能够处理复杂结构程序，开发人员也经常用之于程序自动测试[2]、程序缺陷检测[3]、测试用例生成[4]等。

1 相关研究工作

1.1 符号执行

符号执行使用符号值而非真实用例作为输入值，并将程序变量的值表示为符号表达式[5]。因此，由程序计算的输出表示为符号输入的函数[6]。也就是说，每个符号执行的结果等同于大量测试用例，以便尽可能地检测程序中可能出现的行为和状态是否满足安全性能。符号执行技术分类主要包括以下几种。

(1)经典符号执行技术。主要特点为在理论上可以遍历更多的程序，但不能探索路径约束条件下可能无法处理的可行执行，故并未得到广泛应用。

(2)动态符号执行技术。主要有Concolic测试[7-8]和EGT(Execution-Generated Testing)[9]等，能够利用对实际输入得到的分支路径判定条件进行逻辑取反来探索所有可能的路径，如EXE[10]和KLEE[11]工具和扩展的EGT方法等。该技术在软件测试、逆向工程等应用方面得到认可。

在动态符号执行时，外部代码的交互、约束求解(本文暂不过多讨论)因超时而降低精确性[1]，在使用真实用例缓解该问题时也破坏了路径遍历的完整性，其本质问题依然是路径爆炸和约束求解的难解，故其成为动态符号执行的技术瓶颈之一。优化路径选择可缓解上述问题，相关研究主要包括：(1)使用启发式搜索探求最佳路径，提高程序路径覆盖率，加快符号执行速度，包括：① 使用静态控制流图(CFG)选择路径；② 利用先决条件及输入特性进行符号执行，如预条件符号执行方法[4]、利用静态分析工具来分析程序中缺陷语句的方法[12]等。(2)利用程序分析技术减少路径探索的复杂性，包括：①构建函数和循环摘要供后续重用，如Concolic执行提出的可动态生成函数摘要组合方法[7]，可有效重新利用分析结果；② 剪枝冗余路径，如基于程序功能执行流切片技术[13]，通过裁剪掉与功能无关的分支路径来提高制导效率；③通过依赖性分析[14]来有效合并变量状态，提高路径分析的精度；④通过状态合并来缩小路径分支的选择范围，缓解路径爆炸问题，但该方法易降低路径覆盖率。

随着程序中逻辑判定语句的增加，路径爆炸问题越突出，符号执行面临的技术挑战越严峻[15]。

1.2 符号执行树

在符号执行过程中，根据执行路径而生成的树状结构表示定义为执行树，如图1所示。

图1 示例程序及生成的符号执行树

在执行树中，当程序执行到第3节点时，路径约束条件即为(x > 1)∧(x < 10)∧(x>-6)，约束求解器(要解出3个约束条件的解，即算出可达路径的值)；此时若遍历该执行树，路径条数将以指数级数目增长并引发路径爆炸问题。

若执行树中存在一条由n(当n∈Z+)个逻辑节点组成的路径，则程序执行时需对n个约束条件集合求解，当n→+∞时其计算量无疑是巨大的；若此时对易引发路径爆炸的执行树进行分阶段符号执行，则可降低路径爆炸发生的概率和约束条件的求解难度，但须在分阶段符号执行前探测执行树的深度。

1.3 圈复杂度

圈复杂度(Cyclomatic Complexity)[16]是用来衡量程序代码判定结构复杂程度的重要标准，其值越大说明代码的判断逻辑结构越复杂，即代码质量低或难于测试及维护，存在潜藏缺陷和漏洞的可能性就越大。

一般情况下，增加圈复杂度的核心问题实际是大量的逻辑判定语句，表现在代码上是case、if、while等语句及函数调用，而圈复杂度的计算有利于控制程序逻辑长度、设置检查点(或测试点)和评测代码质量。

定义1圈复杂度值VCC=e-n+2，其中e、n分别表示代码对应控制流图中边数和节点数(含起点和终点，当有多个终点时只计算1次)。

定义2圈复杂度标准量级GCC一般被定义为三个级别：Ⅰ级(代码质量优秀)、Ⅱ级(代码可重构或优化)和Ⅲ级(强制重构)，如公式(1)所示。

(1)

针对路径爆炸问题，本文提出了基于圈复杂度的阶段动态符号执行模型(Cyclomatic Complexity-based Stage Dynamic Symbolic Execution Model，CCSDSEM)，建立利用圈复杂度来探测圈复杂度高的代码段，然后以符号化逻辑判定分支数量作为衡量标准，分阶段进行动态符号执行操作，并在分段处进行约束集求解及优化，进而降低求解的复杂度。本文贡献如下。

(1)分段策略可降低程序逻辑判定分支的规模，缓解路径爆炸现象。

(2)利用分段执行和优化约束条件求解，可提高符号执行的执行效率和路径覆盖率。

2 基于圈复杂度的阶段动态符号执行模型

2.1 模型定义

将待测代码作为模型外部输入数据并计算各检查点的圈复杂度及代码量，然后在统计结果的基础上根据求得的圈复杂度与阈值进行比较，来预判动态符号执行的计算量级，并据此设置检查点来分段执行对应的代码段，在运行符号执行引擎后分别生成缺陷报告。

定义3：将基于圈复杂度的阶段动态符号执行模型定义为一个四元组CCSDSEM=(I,P,E,O),其中：

(1)I=(ISC1,ISC2,…,ISCi,…,ISCn|i,n∈Z+)表示该模型中被测序的源代码(Source Code,SC)。

(2)P=(PCQ,PLC,PIE,PCT,PSSN)表示对测试对象按一定策略进行系列处理;其中PCQ表示统计代码量(Code Quantity,CQ),PLC表示统计循环条件(Loop Condition,LC),PIE表示按照约束规则进行信息提取(Information Extraction,IE)，PCT表示计算阈值(Calculate the Threshold,CT)，PSSN表示按逻辑结构进行阶段节点设置(Set Stage Node,SSN)。

(3)E=(ESG,ESEE)表示对处理后的对象进行符号执行；其中ESG表示符号生成器(Symbol Generator,SG)，ESEE表示符号执行引擎(Symbol Execution Engine,SEE)。

(4)O=(ODR1,ODR2,…,ODRi,…,ODRn|i,n∈Z+)表示输出的各个测试报告，其中ODRi表示输出的第i个缺陷报告(Defect Report,DR)。基于圈复杂度的阶段动态符号执行模型框架如图2所示。

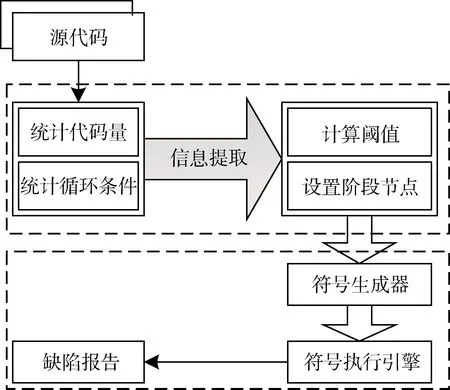
图2 CCSDSEM框架

2.2 分段执行规则

为便于阐述分段符号执行策略，现构造部分代码如下：

(1) int x,y,z,t;

(2) int t;

(3) scanf("%d,%d,%d",&x,&y,&z);

(4) if (x<1) t=x;

(5) else if (x>10) t=2×x-1;

(6) else if (x+y>10) t=2×y+x;

(7) else if (z<0) t=x+z;

(8) else if(y<12) t=y-z;

(9) else t=fun(x);

(10) printf ("%d ",t);

(11) int fun(int n)

(12) { int m;

(13) m=2×fun(n-1)+1;

(14) return m; }

(1)Concolic执行过程

在测试过程中，Concolic执行会随机产生输入测试值(如{x=3,y=13,z=5})，当执行else if (x>10)时，符号化执行会生成路径约束(x0>1)，然后Concolic执行对逻辑判断条件取反并对(x0<1)求解，并将得到的一个测试用例作为输入，从而执行不同路径。

同理，第5行产生约束条件(x0>=1)∧(x0>10)以及(110)∧(z0>0)∧(y0<12)并对约束求解；随着程序执行的不断深入，约束条件复杂性变大，路径分支将会以指数级增长，加大了约束求解难度。

如果圈复杂度超过预先设定阈值Ф时，则对该部分代码进行分段执行或优化约束条件后再执行；此时，因(y0<12)是取反的分支约束条件，对(y0<12)分支无任何影响，故可去掉对z的约束，可从当前路径条件中移除与当前分支结果无关的约束，提高约束求解效率，降低因约束条件过于复杂而引发路径爆炸的概率。

(2)分阶段动态符号执行

当在CCSDSEM框架中执行分阶段动态符号执行时，根据控制流顺序设置检查点并计算对应代码段的圈复杂度，当某个圈复杂度大于预先设定的阈值Ф时，则对该段代码单独执行动态符号执行；反复运用此策略，直至所有代码检测并分解完毕，算法描述如下：

算法：分阶段符号执行策略算法

输入:C语言格式的待测代码

输出:高圈复杂度函数名称及复杂度值

(1) 初始化CCSDSEM=(I,P,E,O)

//初始化模型

(2) 构建待测代码集I

(3) int Ф=50;

//设定阈值Ф=50

//遍历各函数并计算函数的圈复杂度VCC

(4) int CC(Fi);

//计算VCC

(5) { inti=0;

(6) while (I!=NULL)

//当输入集非空时执行

(7) {i++;

//第i个函数

(8) VCC =count (read (Fi));

//读取函数Fi并求出VCC

(9) if (VCC>Ф)

//若VCC大于Ф

(10) { outputFi,VCC;

//输出VCC

(11) temp_filei=read(Fi);

//读取Fi代码到temp_filei

(12) CC (temp_filei);}

//递归计算Fi的VCC

(13) else Symbolic_ Execution (Fi)；

//符号执行Fi

(14) }

(15) }

当程序的整体影响处于可控状态下，采用此策略对被测程序按阈值进行分阶段动态符号执行，可降低产生路径爆炸的概率，缓解因动态符号执行将部分值实例化而引发的路径覆盖不足等问题。

3 实验与分析

本文实验通过SourceMonitor对开源项目GNU Binutils-2.14中部分源代码文件进行圈复杂度测试，选用VCC值较高的源代码文件readelf.c进行测试。

3.1 圈复杂度计算实验

实验进一步对readelf.c计算圈复杂度，与本研究有关的详细信息如表1所示。

表1 readelf.c测试后的主要信息

在readelf.c中，以函数为检查点计算圈复杂度，可看出最复杂函数switch()(在分支语句控制下各函数名相同但内部代码实际是不同的，即各函数的VCC值不同)的VCC值非常高(值为517)，进一步计算得出各功能函数的详细信息，如表2所示。

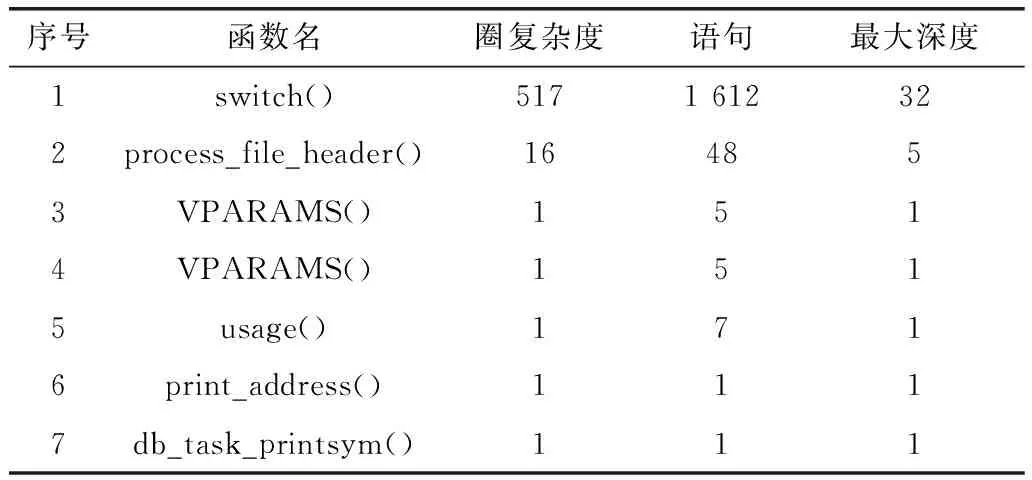
表2 readelf.c测试后的主要信息

显然switch()为readelf.c的主要函数，而且明显高于其他函数，从其Kiviat图(如图3所示)上可以看出各项指标严重偏离合理区间(深色圆环区域)。

图3 Kiviat图

对所有switch()函数计算VCC，累计97个(其中I级55个，II级14个，III级28个)，VCC最高为95，最低为2；在III级中VCC>50的switch(*)如表3所示。

表3 复杂度大于50的含参switch()函数

3.2 分阶段动态符号执行实验

在对测试所得的VCC实验数据分析后发现：若分支情况越多、嵌入层次越深、调用函数越多且复杂，则VCC值越大。因符号执行在VCC越大的情况下效率会严重降低，若将一个复杂程度分解为多个复杂度相对理想且内聚性强的代码片段来进行分阶段符号执行，显然具备缓解或降低路径爆炸的功效。

此部分实验选用符号执行工具KLEE 2.0，CPU为Intel(R) Core(TM) i5-3320M 2.60 GHz、内存为16 GB、Ubuntu 16.04.11 LTS、内核版本为5.4.0-6，编译器clang version 6.0.1，与KLEE相关如llvm6.0，clang6.0。实验首先对将VCC>Ф(Ф设为50)的switch()函数调用采用剪枝处理(会影响代码调用，但会简化与其对应的执行树)，VCC值越大该方法越有益。此外，实验中对于case语句非常多的情况，采用简单以Ф值为上限的简单分割方法，分割后代码段的VCC≤Ф；分阶段动态符号执行后的数据及原因分析如表4所示。

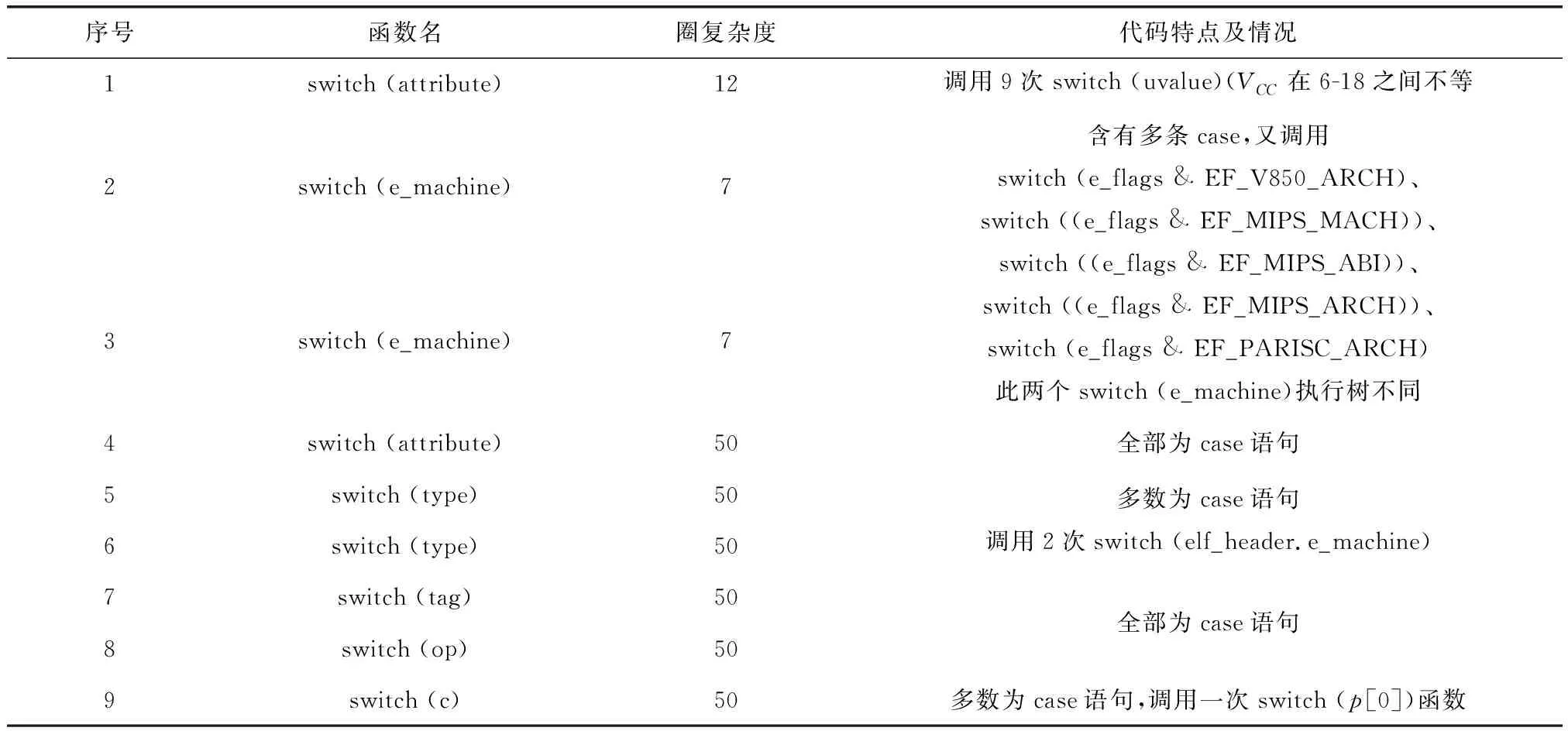
表4 部分含参switch()分阶段执行后的复杂度

3.3 局限性分析

(1)执行分阶段动态符号执行时，具体逻辑判断语句(如case、if)及嵌套层次严重影响分阶段情况，相对应测试的圈复杂度之间差别也很大；尤其代码中case语句趋向全部时，最简单的分阶段方法为：当case语句数量等于Ф时进行分割(存在误判)，此时VCC=Ф(如表4中序号4～9情况)。如果循环或递归的终止条件是符号化的，就可能会出现无限数量的对应路径，因此对循环分支数量的判定结果是衡量符号执行树状状况的重要依据。

(2)实验情况可以判断出动态符号执行中可能产生路径爆炸的不同规模。目前这种方法并不能完全固定分支的数量，故每次实验时结果存在误差，但总体上可以满足圈复杂度不高于Ф的条件。

(3)本实验只对单个.C程序文件进行测试，尚未对大型项目代码进行测试，也未考虑各文件之间的依赖关系等。

4 结论

本文首先介绍动态符号执行的相关研究现状和基本概念，然后详细分析存在的不足以及采用的分阶段执行方法，并分析路径覆盖率，进而提出基于圈复杂度的阶段动态符号执行的方法，并通过示例实验证明，相比于原有的方案，使用CCCSDSEM优化框架后降低了代码的圈复杂度并缓解了路径爆炸。

后续的研究工作主要从以下方面开展：(1)在KLEE分支状态跟踪中收集实际执行的路径数量并做出相应的判断及缓解路径爆炸的策略；(2)如何更好地结合圈复杂度的进行分段优化，并在KLEE中做相应改进是后续研究工作中的重点；(3)如何在分阶段动态符号执行过程中提高约束求解效率；(4)如何保证圈复杂度设置的值既不让程序分割过多而消耗系统资源，又可一定程度上遍历更多的路径且缓解路径爆炸和约束求解。