基于RUSBoost算法的违约风险预测模型构建与应用
钟华星


【摘要】针对金融借贷数据存在的较严重的类别不平衡问题,构建基于RUSBoost算法的违约风险预测模型。作为一种集成学习方法,RUSBoost算法利用欠采样实现了训练集的类别均衡,同时又通过对基学习器的独立采样有效克服了因欠采样而造成的信息丢失问题,从而实现了对类别不平衡数据的较强适应能力。基于某网络借贷平台的金融大数据,首次将RUSBoost算法应用于违约风险预测,同时也将随机森林、决策树以及支持向量机等数据挖掘方法分别应用于违约风险预测问题,并与传统的Logistic回归方法和最小二乘模型进行对比分析。从实验结果来看,绝大部分数据挖掘模型的预测性能要明显优于传统模型,而基于RUSBoost算法的违约风险预测模型又明显优于其他数据挖掘模型。
【关键词】集成学习;数据挖掘;违约风险;网络借贷
【中图分类号】F832.4 【文献标识码】A 【文章編号】1004-0994(2020)10-0074-7
一、引言
信息不对称是导致金融市场效率不高、风险积聚的重要原因之一。而在新技术条件下,金融行业积累、沉淀了海量的多源异构数据。因此,有必要深入研究如何通过大数据技术缓解金融市场中的信息不对称问题,提升金融市场效率。在此背景下,本文研究了数据挖掘方法,尤其是RUSBoost算法在信用风险评估领域的应用。
金融大数据通常具有模式复杂、维度较高、非线性较强、数据类型较多等特点,而传统的信用风险评估方法(包括Logistic回归、OLS模型等)并不能很好地适应上述数据特征。同时,传统方法在处理海量、高维数据时还面临计算复杂度较高的问题。但数据挖掘方法可以通过模型选择和参数调整适应不同特点的数据,例如:通过特征选择和降维学习可以高效地处理高维数据。此外,利用数据挖掘方法在建模时可以引入更多维度的异构信息。信用风险的分析评估对于提升金融中介效率、控制和预防金融风险具有重要意义。其中,网络借贷的违约风险一直是近几年社会关注的焦点问题。本文将利用某网络借贷平台数据,分别构建基于RUSBoost算法、随机森林、决策树以及SVM算法的违约风险预测模型,并且将上述各数据挖掘模型与传统的Logistic回归方法和最小二乘模型(OLS)进行对比分析。本文首次将RUSBoost算法应用于违约风险预测,从实验结果来看,该算法取得了不错的效果。
正常情况下,大部分网络借贷平台的违约率都在5%以内。这意味着在所获得的数据集中只有不到5%的样本是违约数据,剩余95%以上的样本都是未违约数据。在将数据挖掘方法应用于违约风险预测的过程中,上述类别不平衡(class-imbalance)问题是影响算法性能的主要因素之一。
应对类别不平衡问题的常用方法主要有两类[1] :一种是“欠采样”(undersampling),即从样本数量较大的类别中去除一部分样本数据,使得类别分布更均衡;另一种是“过采样”(oversampling),即通过各种二次采样方法增加某些类别的样本数量。欠采样方法的最大缺点是因舍弃样本数据而丢失了部分信息[2] ,优点是简化了模型的训练过程,缩短了训练时间。过采样方法不存在信息丢失问题,但频繁地重复采样不仅导致数据集规模上升、模型训练的时间成本增加,也容易造成严重的过拟合问题[3] 。本文所采用的RUSBoost算法[4] 是一种结合了欠采样方法与Boosting算法[5] 的混合算法。
二、文献综述
在信用风险研究领域,尤其是针对借款人的违约风险预测问题,主要存在两类方法:一类是以Logistic回归、Probit模型以及OLS等为代表的传统方法;另一类是近几年才开始逐步流行的数据挖掘方法,包括随机森林、决策树以及SVM算法等。目前的多数研究仍以经典的传统方法为主,但传统方法对数据分布有严格的假设前提[6] ,这限制了传统方法的预测效果,使得在大多数情况下传统方法的准确度低于数据挖掘方法[7] 。
因此,现在出现了将传统方法与机器学习方法相结合的新趋势。Khandani等[8] 将CART(Classification And Regression Tree)算法与非参数估计方法相结合,构建了非线性的违约风险预测模型,从而利用交易数据和征信数据预测信用卡持有者的逾期和违约情况。Tsai等[9] 针对消费者信用评级问题,设计和比较了几种不同的统计回归方法与机器学习方法相结合的方式,最后研究发现基于Logistic回归与神经网络的混合模型预测准确率最高。
近年来,数据挖掘方法被越来越多地应用于信用风险领域。Huang等[10] 尝试采用SVM算法对信用卡进行评分,而Lee[11] 则将SVM算法应用于企业信用评级,并且通过交叉验证实验证明了该方法的性能优于传统的统计回归方法。方匡南等[12,13] 首次将非参数随机森林分类方法分别应用于信用卡的信用风险评估以及住房贷款的违约风险评估,实验表明该方法的预测准确率明显高于Logitic模型等其他方法。吕劲松等[14] 针对商业银行信贷资产质量审计问题,通过将属性选择、决策树和SVM算法相结合,可以部分识别影响银行资产质量的贷款记录。针对网络借贷的违约风险预测问题,范超等[15] 以及邹欣[16] 分别比较了不同数据挖掘方法和统计回归模型在预测性能上的优劣,并且分析了影响借款人违约的主要因素。
总之,目前基于数据挖掘方法的信用风险研究并不多,但由于对样本数据和应用场景的限制较少,使得多数情况下数据挖掘方法的性能要优于经典的统计回归方法[7] 。而国内在这方面的研究起步较晚,未来将有广阔的发展空间。
三、基于RUSBoost算法的违约风险预测模型
针对样本数据存在的严重的类别分布不平衡问题,本文将利用RUSBoost算法来构建违约风险预测模型。该算法通过欠采样使得训练数据的类别分布更均衡,同时缩短了训练时间。此外,由于每个基学习器的训练集都是独立采样获得的,因而该算法可以有效克服因欠采样而造成的信息丢失问题。已有研究也表明,相较于其他算法而言,RUSBoost算法是一种更简洁、高效的方法,可以更好地适应类别不平衡问题[4] 。但目前在信用风险领域还没有相关研究,本文首次将该算法应用于违约风险预测。
RUSBoost算法是一种结合了欠采样方法与Boosting的混合算法[4] 。Boosting是一种将多个简单的基学习器提升为强学习器的算法[5] ,最常用的Boosting方法是Freund等[17] 提出的AdaBoost算法。本文中的RUSBoost算法亦是基于AdaBoost算法构建的。RUSBoost算法首先利用初始训练集训练出一个基学习器;再根据当前基学习器的训练误差调整每个训练样本的分布权重,通过增大被误分类样本的权重,使其在后续训练过程中获得更多关注;然后利用调整后的样本训练出下一个基学习器;如此反复迭代,直至生成T个基学习器;最后将根据上述T个基学习器的加权投票结果来预测未标记样本。
RUSBoost算法的流程如图1所示。首先,所有样本的分布初始化为1/m;其次,利用欠采样方法生成训练集St',并且通过对St'中各样本的原有权重进行归一化处理,以获得新分布Λt';然后,在訓练集St'和分布Λt'下训练获得基学习器ht,并且更新最优权重αt和样本分布Λt+1,以用于下次迭代;最终通过T次迭代,输出全部基学习器的加权线性组合。在迭代过程中,RUSBoost算法通过调整样本权重的分布(即增加被误分类样本的权重)来提升后续基学习器的准确率。
四、其他违约风险预测模型
除了RUSBoost算法,本文还分别利用随机森林、决策树以及SVM算法等数据挖掘方法构建对应的违约风险预测模型,以比较各类方法的性能。
1. 随机森林。随机森林是由Breiman[18] 提出的一种基于Bagging策略的并行式集成学习方法。它通过T次随机采样获得T个不同的训练集,并且基于每个训练集训练出对应的基学习器,最后通过投票或者平均的方法集成上述T个基学习器的输出结果。随机森林一般以决策树作为基学习器,并且在训练过程中引入了随机属性选择,即:在每个结点决策树会首先从属性集中随机选择出一个候选子集,然后再从上述候选子集中选择一个最优属性作为决策树的一个划分结点。
与传统决策树相比,随机森林通过引入属性扰动增加了基学习器的多样性,使得其集成后的泛化性能有显著提升。
2. 决策树。决策树是通过属性测试构建出一棵树模型,一般以信息增益为准则来选择最优属性。假设数据全集D在属性a上取值为ai的样本集为Di,样本数量为|Di|,而D中第k类样本占全部样本的比例为pk,则对数据集D按照属性q进行划分后的信息增益定义为:
式(13)表示数据集的信息熵。信息增益越大,说明按照该属性划分后数据集的类别纯度提升越大。所以,决策树模型在每个结点会选择信息增益最大的属性进行划分。
本文采用C4.5决策树算法[19] 构建对应的违约风险预测模型。该算法以增益率为准则来选择最优属性,其定义为:
该式表征了属性a在不同取值下的熵。C4.5算法将先过滤出信息增益高于平均值的属性,再从上述候选属性集中选择增益率最高的属性。这样可以避免算法偏好于取值数目较多的属性。
3. 支持向量机。支持向量机[20] 首先用核函数将样本数据映射到某个高维空间,然后通过构造最优超平面实现高维空间上的线性分类。本文采用高斯核函数构建违约风险预测模型,其定义为:
其中,σ>0为高斯核的带宽。
五、数据描述与变量说明
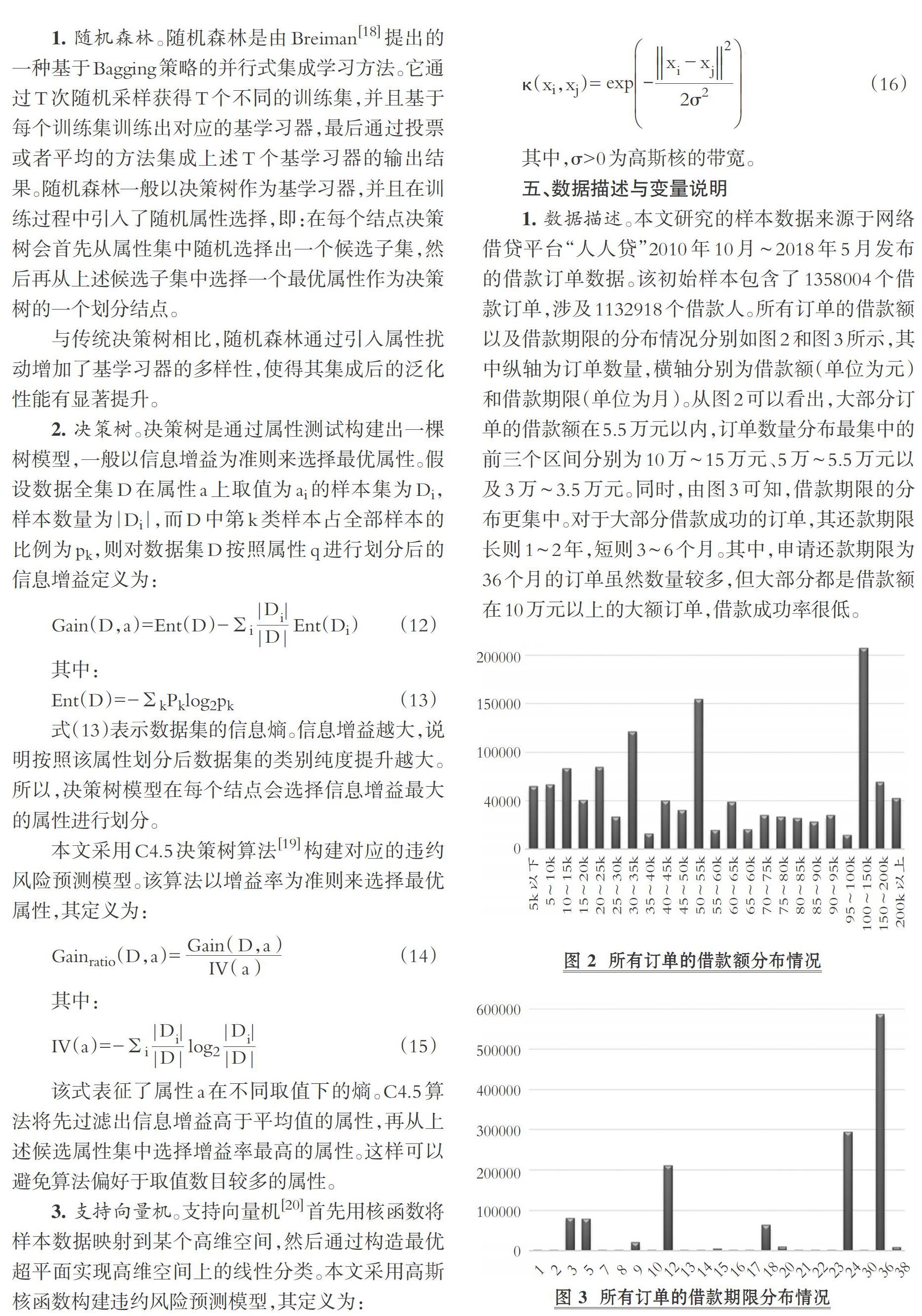
1. 数据描述。本文研究的样本数据来源于网络借贷平台“人人贷”2010年10月 ~ 2018年5月发布的借款订单数据。该初始样本包含了1358004个借款订单,涉及1132918个借款人。所有订单的借款额以及借款期限的分布情况分别如图2和图3所示,其中纵轴为订单数量,横轴分别为借款额(单位为元)和借款期限(单位为月)。从图2可以看出,大部分订单的借款额在5.5万元以内,订单数量分布最集中的前三个区间分别为10万 ~ 15万元、5万 ~ 5.5万元以及3万 ~ 3.5万元。同时,由图3可知,借款期限的分布更集中。对于大部分借款成功的订单,其还款期限长则1 ~ 2年,短则3 ~ 6个月。其中,申请还款期限为36个月的订单虽然数量较多,但大部分都是借款额在10万元以上的大额订单,借款成功率很低。
所有订单被分为4种状态:已流标、进行中、已还清和已违约。其中,已流标订单为579315个,占全部订单的42.66%;进行中的订单为485006个,占全部订单的35.71%;已还清和已违约订单各289431?个和4251?个,占比分别为21.31%和0.31%。
由于进行中的订单暂时无法判断其是否违约,而已流标订单已经借款失败,故在进行违约风险分析时,本文只考虑已还清和已违约两种状态的订单。所以,本文的研究样本共包含了293682?个有效订单,其中违约订单4251个,违约率为1.45%。由于两类订单的样本数量分布严重不平衡,在后续研究中,本文将采用欠采样方法来构建类别均衡的数据集,每次从289431?个已还清订单中随机抽样出4251个样本,再将已获得的8502个类别均衡的样本按照一定比例划分为训练集和测试集。
2. 变量说明。在本文所构建的违约风险预测模型中,其目标变量(被解释变量)是预测订单是否违约。若违约,则目标变量取值为1;否则为0。
同时,本文的违约风险预测模型涉及34个特征变量(解释变量),分为以下6类:①个人基本信息:借款人的性别,出生日期,出生地点,是否已婚。②订单信息:本次借款的借款额,借贷期限,利息率,借款开始时间,借款用途和还款来源。③借贷历史:借款人在本平台上已申请的借款订单数量,以及其中借款成功、已还清和已违约的订单数量;借款人已申请的借款订单的总借款额,以及其中借款成功的借款额与所付利息、已还清的借款额与所付利息。④资产与负债信息:借款人是否有其他贷款,是否有房产,是否有房贷,是否有车产,是否有车贷。⑤工作与收入信息:借款人的收入水平,工作年限,工作职级,工作地点,工作单位类型,所属行业,企业规模。⑥教育背景:借款人的学历水平、毕业学校类型、毕业年份。
本文通过研究发现借款人的收入水平和学历水平对借款成功率的影响较大。不同收入水平借款人的整体占比、借款成功率与违约率情况如表1所示,而不同学历水平借款人的借款结果见表2。
从收入水平来看,月收入在1000元以下的借款人成功率较高,违约率为零,这是因为该层级的订单数量较少、借款额较小,其统计结果可能不具有代表性;月收入在50000元以上的借款人可能存在收入信息证明不真实、借款额较大的问题,导致该层级的借款成功率有所下降、违约率上升。而从其他5个收入层级可以看出,随着收入水平的上升,借款成功率明显提高、违约率逐步下降。
从学历水平来看,高学历借款者的借款成功率更高、违约率更低。其中,研究生及以上学历者的借款成功率低于本科学历者,主要是由于前者的样本数量较少的缘故。
六、实证结果及分析
为了验证各数据挖掘方法的违约风险预测性能,本文采用10折交叉驗证(10-Fold Cross Validation)的方式比较了不同模型预测结果的平均准确率。所谓“10折交叉验证”是将数据集划分为10个规模相等的互斥子集,每次随机选择其中一份数据子集作为测试集,剩余9份子集都作为训练集,从而可以进行10次训练和测试,最终以这10次测试结果的平均准确率来评价每个模型的预测性能。
在10折交叉验证方式下,不同模型的平均准确率如图4所示。这里既包含了RUSBoost、随机森林、决策树以及SVM等数据挖掘模型,也比较了传统的Logistic回归方法和最小二乘模型(OLS)。从图4中可以看出,除SVM模型外,其他3种数据挖掘模型的平均准确率都保持在70%以上,明显高于传统模型。其中,RUSBoost算法的平均准确率最高,达到83.47%;其次是随机森林和决策树模型,分别为79.33%和71.46%。这充分验证了RUSBoost算法在违约风险预测方面的良好性能。
为了进一步分析每个模型对已违约订单和未违约订单两类样本的区分能力,本文采用K-S值(Kolmogorov-Smirnov Statistic)来分析评价每个模型的分类能力。K-S值是针对Kolmogorov-Smirnov检验(K-S检验)构建的统计量,而K-S检验是一种用于检验两个累积分布函数(或者经验分布函数)是否具有显著性差异的非参数方法。由于其不需要假设被检验数据符合正态分布,故该方法非常适合于对不满足正态分布的小样本数据进行假设检验。
若已违约和未违约的样本类别分别表示为c1和c2,则每个类别的经验分布函数为Fci(t)=P[p(x)≤t|ci]。其中,p(x)是由模型预测出的样本属于该类别的后验概率(频率),0≤t≤1。因此,K-S值定义为上述两个经验分布函数之间的最大距离,即:
K-S值最大可以达到1,最小为0。K-S值越大,说明模型对不同类别的区分能力越强,模型的预测准确性也越高。一般来说,K-S值大于0.2即可认为模型有较强的类别区分能力。
不同模型的K-S值比较结果如图5所示。从图5中可以看出,K-S值的对比结果与平均准确率相类似。除SVM模型外,其他3种数据挖掘模型的K-S值明显高于传统模型。RUSBoost算法的K-S值为0.7312,是所有模型中最高的。这主要得益于RUSBoost算法对类别不平衡问题有较强的适应能力,其通过对每个基学习器分别构建不同的训练集,可以有效克服因欠采样而造成的信息丢失问题。
ROC曲线(Receiver Operating Characteristic Curve)和AUC(Area Under Curve)值是另一类常用的分析评价模型预测性能的指标。ROC曲线描述了预测模型的TPR(True Positive Rate)与FPR(False Positive Rate)在不同分类阈值下的变化关系。其中,TPR是指模型预测违约正确的样本数量占全部实际违约样本的比例;FPR是指模型预测违约错误的样本数量占全部实际未违约样本的比例。显然,ROC曲线越靠近(0,1)点,则模型的预测效果越好。因为(0,1)点是所有违约样本都预测正确且对未违约样本没有预测错误的理想模型。而ROC曲线越靠近原点至(1,1)点的对角线,则说明模型的预测性能越接近“随机猜测”。此外,还可以用AUC值(即ROC曲线与横坐标轴围成的面积)比较不同模型的ROC曲线。AUC值越大,则模型的预测性能越好。
不同模型的ROC曲线及其对应的AUC值分别如图6和图7所示。从中可以看出,SVM模型和Logistic回归模型的ROC曲线最接近对角线,它们的AUC值也是最小的。而RUSBoost算法的ROC曲线最靠近左上角,并且基本包含了其他模型的ROC曲线。这说明基于RUSBoost算法的违约风险预测模型是有效的。
七、结论
本文构建了基于RUSBoost算法的违约风险预测模型,并且利用网络借贷平台的金融大数据,对各类基于数据挖掘方法的违约风险预测模型进行了对比分析。从实验结果来看,绝大部分数据挖掘模型的预测性能要明显优于传统模型,而基于RUSBoost算法的违约风险预测模型又明显优于其他数据挖掘模型。这是因为RUSBoost算法利用欠采样实现了训练集的类别均衡,同时又通过对每个基学习器分别构建不同的训练集,可以有效克服因欠采样而造成的信息丢失问题,从而实现对类别不平衡问题较强的适应能力。
本文首次将RUSBoost算法应用于违约风险预测,虽然取得了不错的预测性能,但仍有很大的提升空间。在未来的研究中,可以充分利用金融借贷数据中已经存在的大量文本信息。这些文本数据所蕴含的丰富信息,对进一步提升模型的预测性能具有重要意义。
【 主 要 参 考 文 献 】
[ 1 ] Weiss G. M.. Mining with rarity: A unifying framework[ J].ACM SIGKDD Explorations Newsletter,2004(1):7 ~ 19.
[ 2 ] Batista G. E., Prati R. C., Monard M. C.. A study of the behavior of several methods for balancing machine learning training data[ J].ACM SIGKDD Explorations Newsletter,2004(1):20 ~ 29.
[ 3 ] Drummond C., Holte R. C.. C4.5, class imbalance, and cost sensitivity: Why under-sampling beats over-sampling[C].Workshop on learningfrom imbalanced datasets II. Washington,DC: Citeseer,2003:1 ~ 8.
[ 4 ] Seiffert C., Khoshgoftaar T. M., Van Hulse J., et al.. RUSBoost:A hybrid approach to alleviating class imbalance[ J].IEEE Transactions onSystems Man & Cybernetics Part A Systems & Humans,2009(1):185 ~ 197.
[ 5 ] Freund Y., Schapire R., Abe N.. A short introduction to boosting[ J].Journal-Japanese Society for Artificial Intelligence,1999(771-780):1612.
[ 6 ] Hill R. C., Griffiths W. E., Lim G. C.. Principles of econometrics[M].New Jersey: John Wiley & Sons,2018:196 ~ 315.
[ 7 ] Goyal A., Kaur R.. Accuracy prediction for loan risk using machine learning models[ J].International Journal of Computer Science Trendsand Technology,2016(1):52 ~ 57.
[ 8 ] Khandani A. E., Kim A. J., Lo A. W.. Consumer credit-risk models via machine-learning algorithms[ J].Journal of Banking & Finance,2010(11):2767 ~ 2787.
[ 9 ] Tsai C. F., Chen M. L.. Credit rating by hybrid machine learning techniques[ J].Applied Soft Computing,2010(2):374 ~ 380.
[10] Huang C. L., Chen M. C., Wang C. J.. Credit scoring with a data mining approach based on support vector machines[ J].Expert Systemswith Applications,2007(4):847 ~ 856.
[11] Lee Y. C.. Application of support vector machines to corporate credit rating prediction[ J].Expert Systems with Applications,2007(1):67 ~ 74.
[12] 方匡南,吳见彬,朱建平等.信贷信息不对称下的信用卡信用风险研究[ J].经济研究,2010(1):97 ~ 107.
[13] 方匡南,吴见彬.个人住房贷款违约预测与利率政策模拟[ J].统计研究,2013(10):54 ~ 60.
[14] 吕劲松,王志成,隋学深等.基于数据挖掘的商业银行对公信贷资产质量审计研究[ J].金融研究,2016(7):150 ~ 159.
[15] 范超,王磊,解明明.新经济业态P2P网络借贷的风险甄别研究[ J].统计研究,2017(2):33 ~ 43.
[16] 邹欣.基于数据挖掘模型的违约风险分析——以网络借贷为例[ J].上海金融,2018(5):16 ~ 23.
[17] Freund Y., Schapire R. E.. Experiments with a new boosting algorithm[C].ICML,1996:148 ~ 156.
[18] Breiman L.. Random forests[ J].Machine Learning,2001(1):5 ~ 32.
[19] Quinlan J. R.. C4.5:Programs for machine learning[M].California: Elsevier,2014:17 ~ 80.
[20] Cortes C., Vapnik V.. Support-vector networks[ J].Machine Learning,1995(3):273 ~ 297.

