“教学三法”催生学生自主学习力

程敏

【摘要】学习力是学生核心素养的核心能力。数学学习力包括分析、计算、推理、想象、创造等能力。作为教师，我们应通过概念的形成、规律的得出、模型的建立、知识的应用、小组的交流等，因势利导地培养学生的自主学习力。“授之以鱼不如授之以渔”，如此方能越教越轻松，方能达到“教是为了不教”之境界。

【关键词】因势利导 催生自主 小组交流 学习力

一、诸葛亮锦囊法

古有“诸葛亮的锦囊——神机妙算”，锦囊是在关键时刻设置的疑问以及解开疑问的法宝。在教学中，教师如能向诸葛孔明学习，领略教学的前瞻性，预计问题于合适的时机，以课前为起点追踪到课中甚至是课后，因势利导，就能很好地把握一节课的预设与生成。

【案例】《圆的认识》。

“圆”在我们的生活中无处不在，并成为美的使者和化身，圆盘、圆圈、圆片、圆孔、圆木……要求学生利用桌面上“圆”的材料和模具来画圆并剪下来。

师：刚才，同学们利用生活中“圆形”模具制作出了圆。下面，请同学们动手折一折、量一量、比一比、画一画，研究研究，相信大家一定会有新的发现。两点小小的建议：第一，研究过程中，别忘了把你们组的结论，哪怕是任何细小的发现都记录在学习纸上并一起来交流。第二，如果觉得没啥研究了，别急！老师为每个小组准备了“锦囊”：一份研究提示，到时候打开看看，或许对大家的研究会有所帮助。

锦囊一：“圆，一中同长也。”（早在两千多年前，墨子在他的著作中这样描述道。古人讲的“一中”指什么？“同长”又指的是什么呢）

锦囊二：“圆的半径和直径有多少条？”（把一个圆对折，对折，再对折，这样一直对折下去，展开后你们发现了什么）

锦囊三：“圆的直径和半径的关系。”（折一折或量一量，圆直径的长度和半径有什么关系？如果不是同一个圆或等圆呢）

锦囊四：“圆心与半径的作用。”（圆心确定圆的什么？半径又确定圆的什么）

锦囊五：“没有规矩不成方圆。”（尝试用圆规或用圆规以外的其他物品画圆，发现画圆时要注意什么）

在教学中，秉承充分尊重和相信学生的学习能力，准确把握教学的起点，并前瞻性地预设教学中可能出现的重难点所在，将其以“锦囊”的形式巧妙地呈现，在学生需要的时候加以点拨，可收到事半功倍的效果。

二、阿凡提金币法

阿凡提“以连续15天借金币，第1天借1个，以后每天都是前一天的2倍，1，2，4，8，16，32，64……金币一共是1+2+4+8+-- -+16384=32767（个）”使愚弄百姓、贪得无厌的高利贷者受到了惩罚。阿凡提金币法，是利用数字之间的累计与变换关系让学生感受并学会数字的奇妙无穷与变化多端，用于数学教学中别有一番风味。

【案例】《摆一摆想一想》。

不同的数摆放在不同的数位上，数值便有所不同，通过“摆与想”找出其中的规律所在。

师：阿凡提有一个金币，这是几？（摆放在个位上，这是1）让阿凡提来给我们变一变（出示数位表），这是几？（摆放在十位上，这是10）

瞧，多有趣啊！把1个圆片放在数位表的不同位置上就能表示不同的数。

师：阿凡提想考考同学们，他有2个金币，可以摆出几个不同的数字？

要求：两个学生小组合作，一个学生摆，另一个学生在学习单上把摆的金币数用圆片表示，边画边记录（2，11，20）。请两个组汇报比较，初步感受有序的思维方式，并引導学生从大到小或从小到大排列。

师：现在阿凡提拿出了3个金币，又可以变出几个不同的数字呢？

要求：四个学生小组合作，不再用实物摆，而在表格中直接用画圆片的方式表示，边画边记录。学生活动教师巡视，选择有代表性的作品展示，30，3，1 2，21（交换位置排列）;30，21，1 2，3（从大到小排列）;3，1 2，21，30（从小到大排列）。

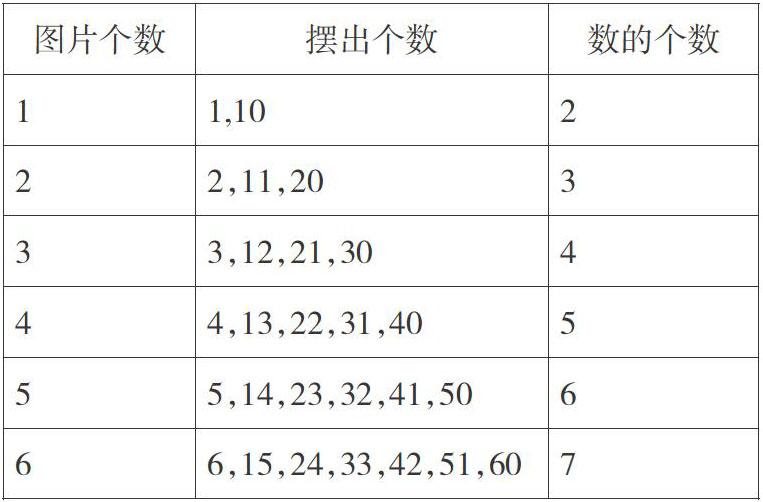
师：阿凡提的金币继续增加到4个，5个，6个呢？请思考并直接在表格上记录下来。

师引导学生观察上表，你发现有什么小秘密吗？如摆出数的个数比圆片的个数多1;又如：摆出的数十位和个位上的数字加起来都等于圆片的个数等。

师：阿凡提金币的秘密被聪明的同学们给破解了，那么下面这组数是用几个金币变的？

出示：9， 18， 27， 36， 45， 54， 63， 72， 81， 90（9个，为什么）

师：最后，阿凡提拿出了1 0个金币，能摆出几个数？是哪几个？（11个）

写数：100， 91， 82， 73， 64， 55， 46， 37， 28， 19，10

师：一定是这样吗？阿凡提请同学们仔细观察，这11个数中有没有不符合要求的数？

“金币”再次让学生陷入思考：100是用1个圆片摆成的;10也是用1个圆片摆成的，根本无须10个圆片，得删除。看来，10个圆片只能摆9个两位数，之前探索出来的规律并不适用于10个金币。此时学生会心地点点头，在思辨中明确了真正的规律之所在。

三、世界咖啡屋法

世界咖啡屋法，是指“围绕一个相关的问题有意图地建造一个实时的集体会议，通过将大家的思维和智慧集中起来解决问题，发现思考的共性过程”。将其引入常见的小组合作学习模式中，可以有效地催生学生的自主学习力。

【案例】《直线、射线、线段》。

“三线”本为一体：当线是有限长时，两端的点就是端点，这是线段;将线段的一端无限延长便形成了射线;将另一端也无限延长就是直线，三线之间可以互相转化，线段、射线又是直线的一部分。

（1）师：老师这里有一个教具，从一端到另一端可以看作是一条线段，我们把它叫作①号线（线段）。现在，从这个教具的一端射出一条光线，它照射在老师的手上，请问现在这条线段应该是从哪儿到哪儿，一端的端点在这儿，另一端的端点在哪儿？（继续将光束照射到更远处：学生身上、墙上、天花板上）

（2）师：同学们，插上想象的翅膀。假设我站在操场上，上面没有任何障碍物阻挡，我们将光线射向天空，那么这一端的端点在这儿，另一端的端点在哪儿？（另一端没有端点，无限延长）那么，它还是线段吗？（不是）为什么？现在我们称之为②号线。

（3）师：我们回到教室，假设这一端的光线没有任何障碍物阻挡，它在无限延伸。接着从教具的另一端也射出一条光线，它也没有任何障碍物阻挡，它也在无限延伸，也就是说原来线段的两端都在无限延伸。请问它的两端有端点吗？（没有）它是①号线吗？是②号线吗？（都不是，为什么）那我们称之为③号线。

接着，师用表格的形式引导学生通过小组合作将头脑中形成的初步印象进行归纳和整理，表格以①号线、②号线、③号线为主线，依据学生在思维过程中可能遇到的问题加以展开，“我来给它们取个名字”“我来画画它们的样子”“有端点吗？有几个？”“能不能向一端或两端无限延伸？”“能度量出长度吗？”“它们有什么相同和不同的地方？”

引入“世界咖啡屋”教学法，先启动小组合作交流，选出组长做好记录;接着，组长作为本组代表进行轮换交流，即A组至B组，B组至C组，以此类推，并完善记录，如此轮换几次;最后，组长回到本组将“喝咖啡”的结果向本组交流。此法较之单纯的小组合作学习更为有效，达到了全班学生间的思想交流目的，学生自主逐步归纳、整理出“三线”之间的联系与区别。

教学反思：陶行知先生说“我以为好的先生不是教书，不是教学生，乃是教学生学”，叶圣陶先生也说“教师教任何功课，‘教都是为了达到用不着‘教”，叶圣陶先生與陶行知先生都精辟地概括了教学的本质——教会学生自主学习。在以上三个教学实例中，教师在教学时均给予了学生充分的独立思考时间与小组合作时间，“诸葛亮锦囊法”是在学生自主探究的基础上，在学生学习进程受挫内心产生真正需要时，主动去寻求提示;“阿凡提金币法”集中体现了十进位值制计数法中的重要概念，0—9这10个数字放在不同的数位上就能表示不同的数，而这些数的获得是学生不断由具体实物到抽象数字再到规律形成的结构化体验;“世界咖啡屋法”则是学生小组合作学习交流的最好体现，既有同组间的合作更有异组间的交流，旨在让学生主动去获得数学活动经验。如上“三法”课堂教学，努力尝试以学生为中心的教学理念，让学生独立思考、小组研究、交流表达，师生间、学生间彼此思想产生碰撞，给学生留有足够的时间和空间去做、去想、去说、去悟，努力催生出学生的自主学习力。

【参考文献】

[1]华应龙.我这样教数学——华应龙课堂实录[J].小学教学（教学版），2010（ 5）.

[2]王永春.小学数学核心素养体系下的运算能力[J].学教学研究（教学版），2017（3）.