基于峰谷电价的光伏储能系统研究与应用

马雪松，鞠振河，靳龙飞

（沈阳工程学院a.研究生部；b.新能源学院，辽宁 沈阳 110136）

随着煤炭、天然气等不可再生能源的使用，这些能源的储量正逐渐降低；同时，开采、使用、运输过程使这些不可再生能源造成环境污染。为了使人类今后的发展不受限制，开发新的能源种类刻不容缓。现如今，风能、太阳能是能源行业的中流砥柱。然而，新能源技术相较于传统能源仍处于落后地位，比如太阳能的应用规模比火力发电小很多，主要原因是光伏发电输出的电能质量差，这种情况可能会对电网造成冲击。随着光伏发电技术的逐渐提高，光伏发电装机容量将超过火力发电是必然趋势[1]。

1 光伏发电的原理

光伏发电是基于光生伏打效应的一种发电技术。光生伏打效应就是当物体受光照时,物体内的电荷分布状态发生变化而产生电动势和电流的一种效应。当太阳能电池被太阳光照射时，由于太阳能电池的主要材料是半导体，光子能量会被半导体材料吸收。电子吸收能量后会发生自由移动，在这种运动的作用下，半导体材料里将产生电子-空穴对。电子-空穴对可视为带有负电荷-正电荷的粒子，因此其也被称为光生载流子。太阳能电池是一块巨大的PN结，P区和N区直接接触。N区的光生载流子运动至P 区和N 区的边界面时，由于PN 结的物理性质，其接触面存在由P 区指向N 区的光生电场。在这个光生电场的作用下，太阳能电池中带正电荷的空穴沿着电场方向做定向运动；同理，带负电荷的电子沿着电场反方向定向运动。这种定向运动就产生了光生电流，即为光伏电池的输出电流。光伏电池产生的直流电可以通过逆变器逆变成交流电流。这个电流可以被负载使用，也可通过控制器为蓄电池充电。这就是光伏发电的原理[2]。

2 峰谷电价

为了实现社会、经济、能源等可持续发展，必须对需求侧进行经济管理，而其中实行峰谷分时电价制度是一种行之有效的方法。目前，世界各国对峰谷分时电价的意义、峰谷电价的定价措施、用户对于峰谷电价的反应以及发电公司、电网公司、用户的成本效益等进行了各种研究，并取得了一定的成果。峰谷分时电价是电网公司提出的一种新的电费收费模式，这种收费方式可以刺激到用户对电价的敏感程度，从而改变用户的用电习惯。峰谷分时电价是把每天的时间按照负荷功率的高低分为峰值电价时段、均值电价时段、谷值电价时段，以均值电价为收费基础，峰值电价的价格更高，低谷电价的价格更低。峰值电价与谷值电价的差距很大，这使得用户更倾向于在谷值电价时段用电。这种举措极大地削弱了峰值功率，填平谷值功率，使电网日负荷更趋于平稳，也可以降低谷值电价时段内电力设备的闲置率，避免或推迟了为满足负荷增长而加入的发电容量，大大降低电网公司的成本，对于运行成本的降低也大有裨益[3]。与此同时，用户不仅为电网的稳定运行贡献力量，也可以减少自身的用电费用，这对于国民经济的发展是极其有益的。此外，采用峰谷分时电价还可以减少负荷在电网传输中引起的电能损耗。目前，对于峰谷值电价的定价标准均是基于平价电价，对其上下浮动比例的比值即拉开比进行推导，以此作为峰值谷值电价[4]。

3 1MW光伏发电储能系统优化方法

本文进行优化的光伏发电系统的概况如表1所示。以东北电网的峰谷电价时段为例，具体参数如表2所示。

表1 光伏发电系统主要参数

表2 东北电网峰谷电价时段 h

对1 MW 光伏发电系统的经济性进行优化。光伏发电利润计算式为

式中，F为光伏发电系统的总利润；F上为国家规定的光伏发电上网统一电价，其值为0.83 元/（kW·h）；F补为国家规定的光伏发电上网补偿电价，按照相关规定，其值为0.32元/（kW·h）。

光伏发电输出功率为

式中，P为光伏发电总输出功率（kW）；Pi为光伏阵列的输出功率（kW）；Po为储能系统的充电功率（kW）。

因此，整个光伏发电系统的净利润可表示为

式中，t1、t2、t3分别为峰值、均值、谷值电价时段内的充电时间。

对储能系统的优化可简化为最优化问题，最优化方程为

式中，V为储能系统直流电压，其值为48 V；C蓄为储能系统的总容量（kW/h）。

使用遗传算法对该最优化方程进行仿真求解，其结果如图1所示。

图1 遗传算法结果

如图2 所示，随着迭代次数的增加，优化目标函数值逐渐降低，达到该优化模型的最优解。

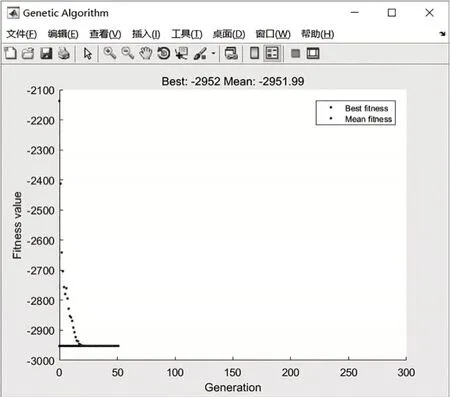
图2 个体适应度迭代过程

图3 所示为优化结果，即储能装置在各个时段内的充电时长。

图3 遗传算法求得最优个体

仿真优化后，储能装置在峰谷电价时段内的充电时长如表3所示。

将表3 数据代入优化目标函数，即可得储能装置优化后系统日均利润，与该光伏电站原始日均收益的比较结果，如表4所示。

表3 储能装置充电时长 h

表4 光伏电站日均收益比较结果 元

4 结 论

针对光伏储能装置经济性差、响应国家峰谷值电价政策迟缓的问题，本文以1 MW 光伏电站的储能装置为优化对象，建立了基于峰谷电价时段的优化模型，并使用遗传算法进行了求解，所得结果如下：

1）简单阐述了光伏发电的基本原理，并介绍了我国推出的峰谷电价政策对于降低电网负荷峰谷差，提供系统供电稳定性，降低用户的用电费用的巨大意义。

2）以光伏电站的日均收益为目标函数，结合充电时段、充电功率约束，建立了针对储能装置的单目标优化模型。

3）通过Matlab运行遗传算法对其求解，得出了储能装置在各时段内的充电时长。将优化后光伏电站的日均收益与优化前进行比较，得出了以该种方式对蓄电池进行充电，可以提高光伏电站日均收益的结论。