裂缝参数对纵波各向异性影响的数值模拟

段 茜 刘向君 梁利喜 熊 健

(①油气藏地质及开发工程国家重点实验室(西南石油大学)，四川成都 610500； ②西南石油大学理学院，四川成都 610500)

0 引言

裂缝描述是油藏开发的重要内容，准确预测裂缝发育带的方向以及最大裂缝密度区域是勘探地球物理的一项重大技术难题。理论与实践均已证实，当地下介质中存在裂缝时，纵波响应呈方位各向异性特征，即沿不同方位具有不同的动力学和运动学参数。因此，可根据裂缝型介质中的纵波响应方位各向异性预测裂缝参数。

自20世纪90年代以来，人们利用不同方位的速度、旅行时、振幅等多种属性预测裂缝。Tsvanskin[1]研究了HTI介质中纵波动校正速度随方位的变化规律，提出采用纵波动校正速度估算横波分裂系数，进而预测裂缝密度。Ruger[2]研究了HTI介质中纵波反射系数随炮检距和方位角的变化，认为振幅与AVO梯度随方位角余弦函数的平方而变化，给出了反射振幅与各向异性系数之间的简单关系。Perez等[3]采用多种方法预测委内瑞拉西南部碳酸盐岩储层的裂缝走向。董渊等[4]设计了一个简单的三层水平界面模型，采用交错网格有限差分方法，在以45°夹角彼此相交的4条二维测线的纵波CDP道集上，通过拾取层间时差求取各向异性参数，并预测地下裂缝发育情况。Shen等[5]利用多信号分类技术，从二维纵波地震数据中提取振幅和频率随炮检距的变化属性检测碳酸盐岩储层的裂缝方向。Li等[6]尝试利用三维纵波地震资料，在中国东部黄河三角洲地区检测裂缝。张立勤等[7]将地震数据划分为5个方位角数据，按不同的方位角范围对地震道进行振幅补偿、校正和叠前时间偏移，产生不同方位角的处理结果，从而预测储层的各向异性特征。杨勤勇等[8]通过建立裂缝物理模型，得到了速度与振幅随测线方位变化的关系曲线，结果表明，当测线方位与裂缝方向平行时反射时间最小、振幅最大，随着测线方位与裂缝走向间的夹角增大，反射时间逐渐增大、振幅逐渐减小，直至观测方位与裂缝方向垂直时，反射时间最大、振幅最小。Zhu等[9]研究了横观各向同性样品的P波衰减系数，认为衰减各向异性远远超过速度各向异性，从而为裂缝探测和岩性识别提供了敏感属性。齐宇等[10]运用物理模型模拟方法，在水中以50、100、150mm的炮检距观测了HTI介质的地震响应，模拟了裂缝介质的反射波振幅、反射旅行时随裂缝方位角变化的规律。王月英等[11]分析了两组任意夹角的倾斜裂缝介质模型的地震波场数值模拟结果，认为在发育强度相同的情况下，倾斜裂缝较垂直裂缝的方位各向异性程度弱，裂缝发育趋于复杂时，各向异性特征趋于减弱。王洪求等[12]分析和对比了旅行时、旅行时差、振幅、AVO梯度的方位各向异性特征及其裂缝预测精度，在此基础上优选有利属性进行融合，进一步提高了裂缝预测精度。王玲玲等[13]基于制作的多参数复杂裂缝储层地震物理模型，利用相干、倾角、振幅、方差、曲率、衰减、频谱分解等属性识别裂缝及优选敏感属性。

尽管基于纵波属性方位各向异性的裂缝预测方法较多，但在岩石物理实验中，人工裂缝模型类型有限且裂缝多为均匀分布，研究结果具有一定的局限性。裂隙介质等效理论在裂缝形状、裂缝间的相互作用、流体作用等方面大多进行了近似或简化处理，难以精细描绘复杂缝洞系统及其流体分布，计算结果通常与实验结果存在较大差异。利用地震资料研究天然裂缝的纵波方位各向异性，目前还缺乏纵波属性对裂缝的敏感性系统分析。为此，本文基于声波波动理论，对随机离散裂缝模型的声波波场进行数值模拟，通过计算不同测线方位的声波速度和衰减系数，分析声学参数与裂缝分布、走向、密度及流体间的关系，以期为裂缝型储层参数预测提供一定的理论基础。

1 声学参数的计算

1.1 计算声波速度

本文对超声波透射实验进行数值模拟，以发射探头的激发信号为震源，模拟其通过不同气/水两相裂缝型岩样后接收探头的波形图，再拾取接收端的波形初至得到波的传播时间，利用

(1)

即可计算声波速度VP。式中：L为岩样长度；TP为纵波传播时间。

1.2 计算声波衰减系数

采用标准样品对比法，将铝块作为标准样品，再取一块与铝块长度相同的岩样作为待测样品，分别提取铝块和岩样的声波首波振幅值，即可利用

(2)

计算岩样的声波衰减系数α。式中：A0和A分别为铝块和岩样的声波首波振幅；α0为铝块的声波衰减系数(实际计算时可近似为0)。

2 裂缝模型及观测系统

2.1 单裂缝模型声学参数试算

基于二阶声波波动方程，对气/水两相裂缝型岩样的声波波场进行有限差分数值模拟。图1、图2分别为铝块、单裂缝岩样声波波场快照，图3为铝块和岩样接收端波形图。由图3可见：从接收端提取的岩样首波初至时间为8.38 μs，由式(1)得到VP为5966.6m/s；从波形图上提取铝块和岩样的声波首波振幅分别为1.0和0.1644，代入式(2)即可计算出该岩样的α为36.11dB/m。

2.2 随机离散裂缝模型的建立

前人已讨论了各类连续随机介质模型的构造方法[14-17]，但这些方法几乎都使用一个均值为零的平稳随机过程表示介质在空间小尺度的非均匀性，这并不适用于描述分布极不规则的裂缝型油气藏。在地壳介质中裂缝都呈离散且随机分布，裂缝的存在使介质的速度和密度发生不连续变化。因此，应将裂缝型介质看作裂缝和基质的结合体，采用离散裂缝模型表征。离散裂缝模型可以表征裂缝性油藏在任意尺度的非均质性，可清楚地显示介质中的每条裂缝，具有计算精度高、拟真性好的优点。基于数字图像处理技术，通过设置孔隙度φ、裂缝密度d、裂缝长宽比r及裂缝倾角θ(裂缝与水平线间的夹角)等裂缝参数，采用邻点融合方法建立非均匀性的随机裂缝介质，构建步骤如下。

图1 铝块声波波场快照(t=8μs)设铝块尺寸为50mm(长度)×50mm(直径)，时间采样步长为10ns，将铝块的纵向剖面区域划分成250×250的网格，因此空间采样步长为0.2mm。震源为主频100kHz的雷克子波，位于(25mm，0)处，接收探头位于(25mm，50mm)处，采用吸收边界条件[18]。铝块纵波速度为6350m/s。★代表震源位置，▲代表接收探头位置，下同

图2 单裂缝岩样声波波场快照(t=8μs)岩样的尺寸、采样步长、纵向剖面区域划分、震源、边界条件等参数同图1。裂缝位于模型中心，缝长为14mm，缝宽为3mm，裂缝与水平线之间的夹角为0°。岩样骨架的纵波速度为6200m/s，裂缝孔隙流体为气/水两相，气和水的密度分别为0.72、1000kg/m3，体积模量分别为0.1、2.1GPa。设孔隙的含水饱和度为50%，在流体替换过程中，按照Wood模型[19]计算出孔隙流体的密度为500.36kg/m3，体积模量为0.19GPa，因此裂缝孔隙流体的声波速度为616.22m/s

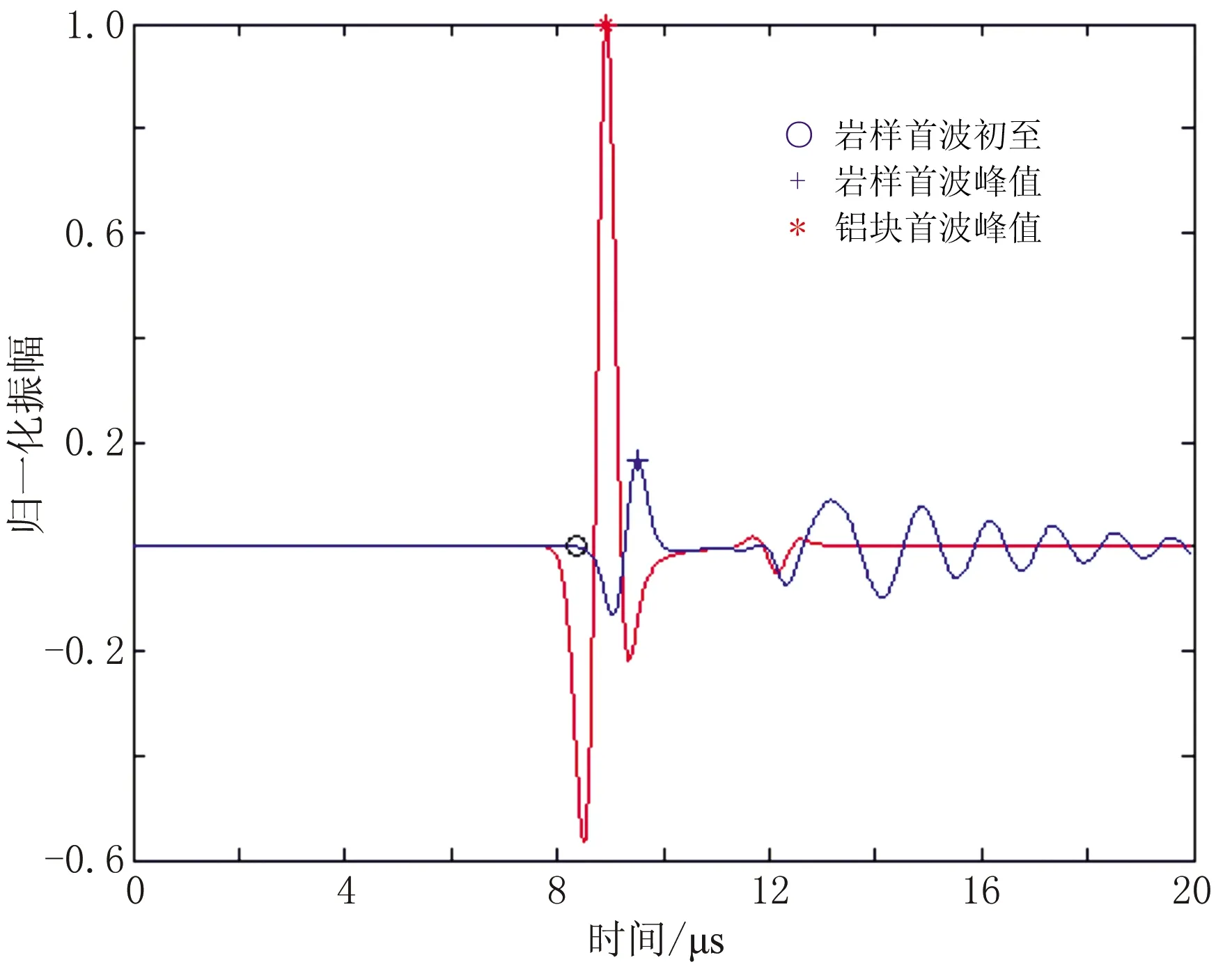
图3 铝块和岩样接收端波形图

(1)选定裂缝模型参数，包括φ、d、r和θ。

(2)根据设置的φ和d，计算给定模型范围内的裂缝的面积s和裂缝条数n。

(3)随机生成n个像素点作为n条裂缝的中心Mn(xn,zn)，按如下步骤逐个融合其邻域内像素，直到模型区域内的所有裂缝面积达到s为止。

1)裂缝的像素点构成的图像子集记为P，将P的邻点构成的图像子集记为N′(P)，其中N′(P)与P无公共像素点。初始时，每条裂缝只包含一个像素点，即P={Mn}。

2)由r确定P中像素点的4个邻域方向(上、下、左、右)的融合概率cj。

3)按照cj随机将N′(P)的像素点M′加入P中P=P+{M′},M′∈N′(P)。

4)若P的面积达到s，则将图像旋转角度θ，否则转步骤3)。

通过选择4个裂缝参数，可按以上步骤构造不同形式的随机裂缝介质模型。

2.3 实验观测系统

图4为纵波方位各向异性特征的实验观测系统。

图4 定炮检距观测系统示意图发射探头与接收探头间的距离固定，并将两探头固定在岩心顶部某一水平面上同时绕中心点逆时针旋转，观测并记录透过模型的超声波速度与衰减特性。测线方位每旋转15°采集1道数据，当测线方位旋转360°(共采集25道数据)时采集1条测线。测线与裂缝走向平行时为0°或180°方位，测线与裂缝走向垂直时为90°或270°方位，以测线与裂缝走向平行时开始观测

3 模拟结果与分析

3.1 裂缝倾角及密度对方位各向异性特征的影响

建立20个随机离散裂缝模型(图5)。由于采用360°观测系统，在研究裂缝方位各向异性特征时将裂缝走向设置成某一固定方位。图6为测线方位与裂缝走向夹角(下文简称测线方位角)不同时模型8的声波位移波场快照。图7～图11分别为模型1～4、5～8、9～12、13～16、17～20的各向异性特征曲线。由模拟结果可见，VP和α随测线方位呈各向异性特征，整个变化以180°为周期，随着测线方位角增大，VP减小(图7a、图8a、图9a、图10a、图11a)、α增大(图7b、图8b、图9b、图10b、图11b)。如：当测线方位角为0°或180°时，VP较大、α较小；当测线方位角为90°或270°时，VP较小、α较大。

图5 随机离散裂缝模型岩心尺寸为50mm(长度)×50mm(直径)，时间采样步长为10ns，空间采样步长为0.2mm。φ=4%，θ=65°，r均值为10，气/水两相裂缝孔隙流体的含水饱和度为50%。从左至右、从上至下依次为模型1～20，模型1～4、5～8、9～12、13～16、17～20的d分别为2000、4000、6000、8000、10000条/m2

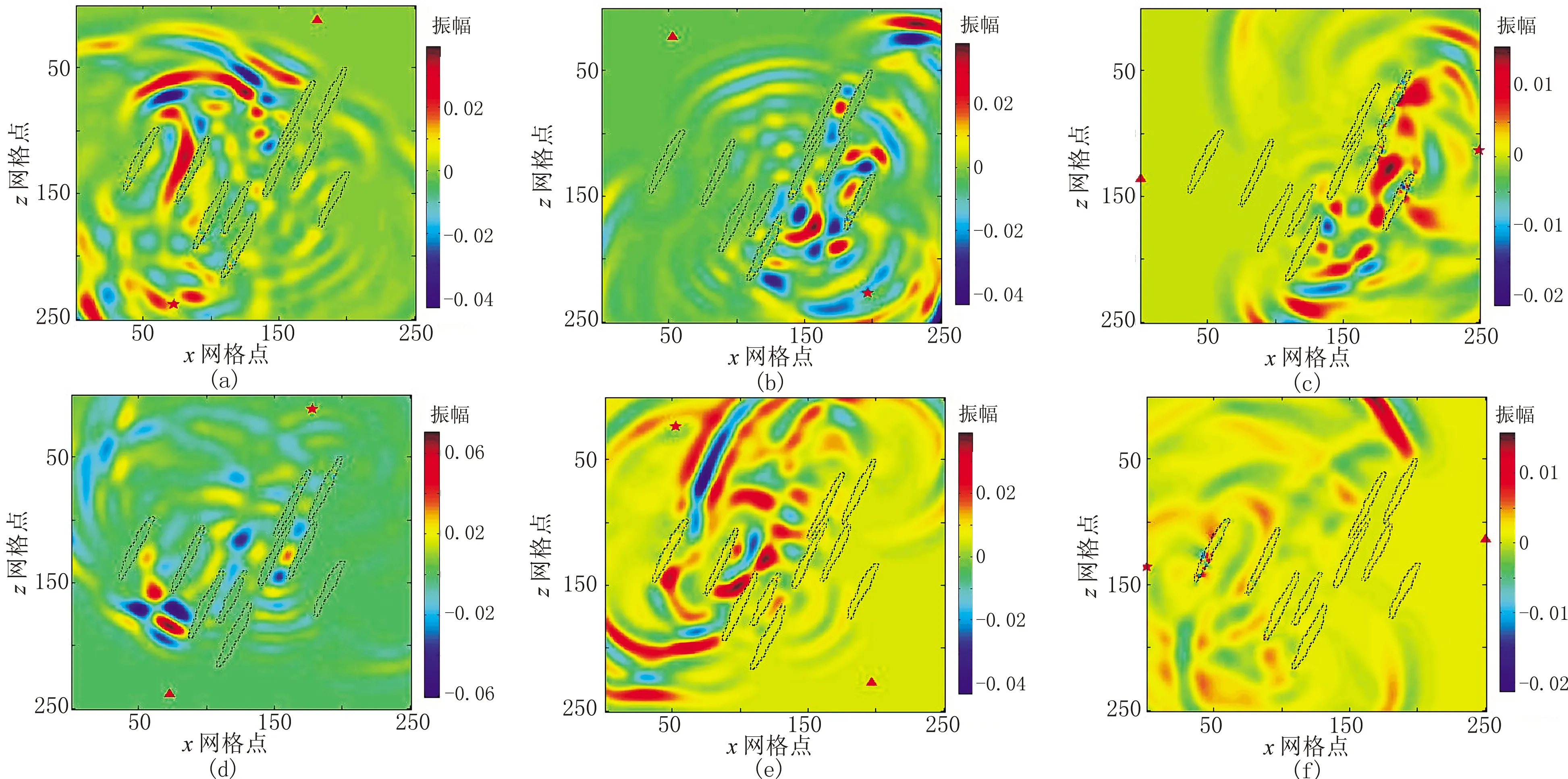
图6 测线方位与裂缝走向夹角不同时模型8的声波位移波场快照(t=8 μs)(a)0°； (b)60°； (c)120°； (d)180°； (e)240°； (f)300°

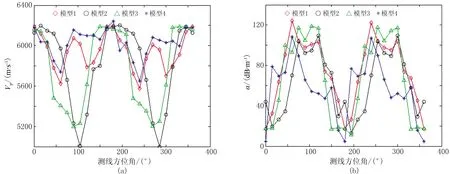
图7 模型1～4的各向异性特征曲线(a)VP随测线方位角变化； (b)α随测线方位角变化

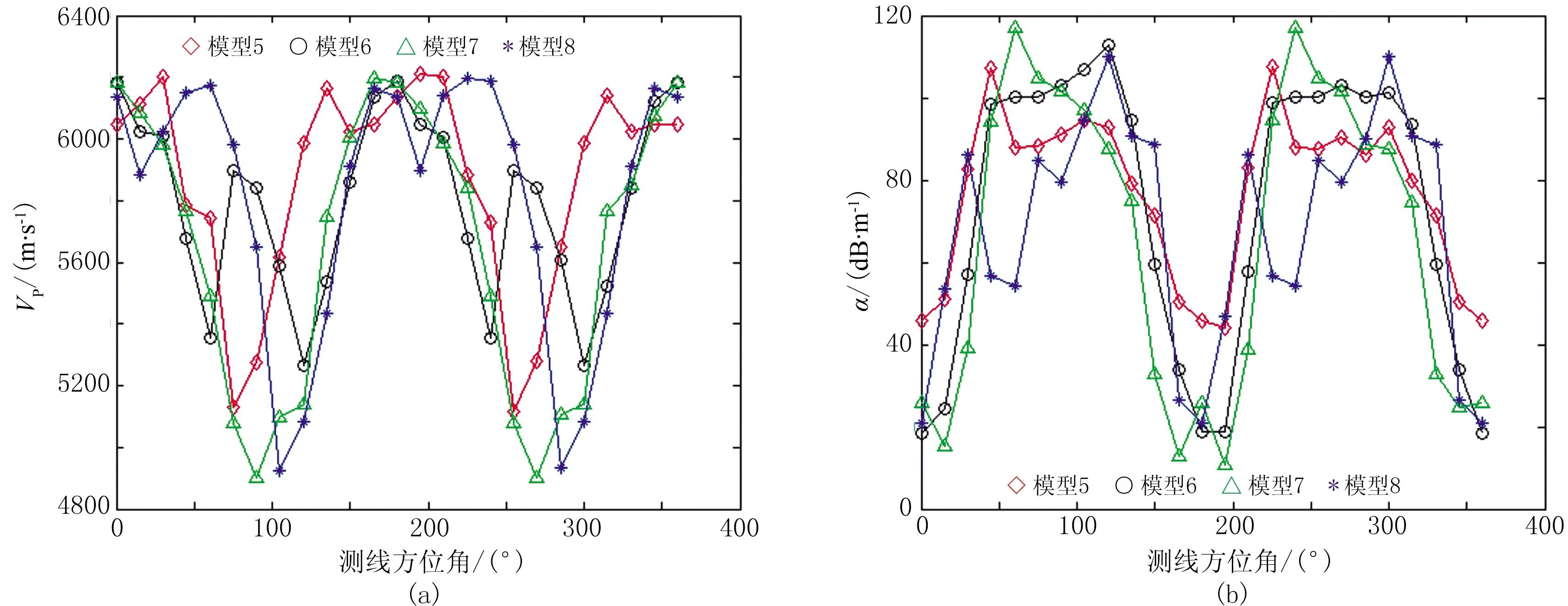
图8 模型5～8的各向异性特征曲线(a)VP随测线方位角变化； (b)α随测线方位角变化

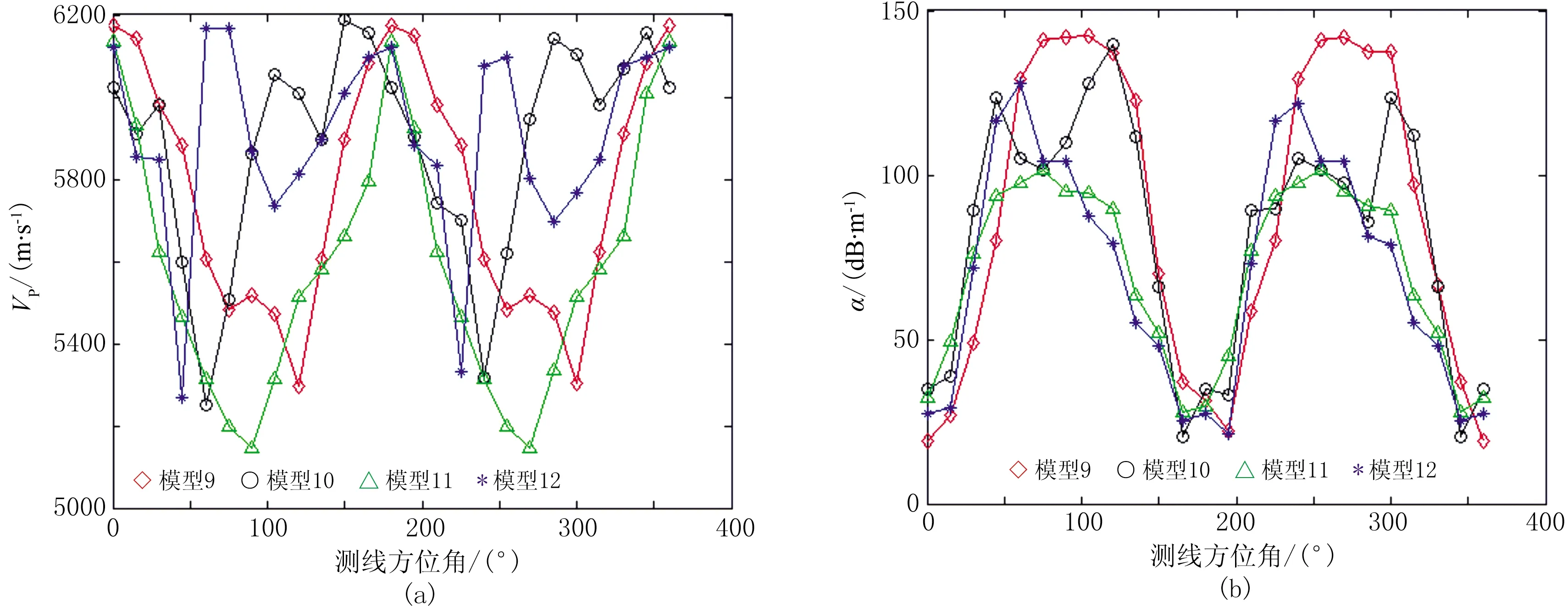
图9 模型9～12的各向异性特征曲线(a)VP随测线方位角变化； (b)α随测线方位角变化

图10 模型13～16的各向异性特征曲线(a)VP随测线方位角变化； (b)α随测线方位角变化

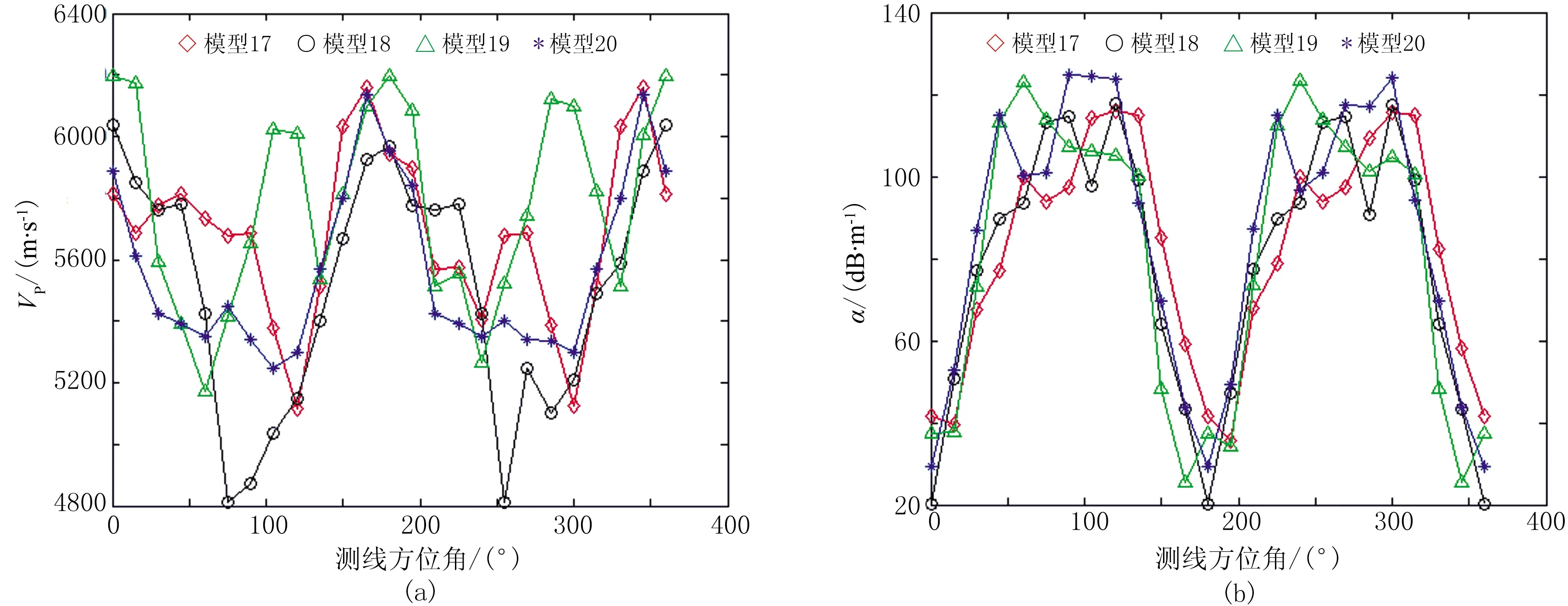
图11 模型17～20的各向异性特征曲线(a)VP随测线方位角变化； (b)α随测线方位角变化

以模型8为例。VP在测线方位角为0°或180°时较大，在测线方位角为60°和240°时出现极大值，在测线方位角为90°时并未达到最小值，而在测线方位角为105°和285°时值达到最小值(图8a)。这是因为裂缝分布是随机离散的，除了在测线方位角为0°或180°时，在其他测线方位角声波绕射通过裂缝到达接收端的路程也可能较短，因此VP较高。VP变化曲线呈多峰值分布，且随着裂缝密度d增大，多峰值分布现象越明显。因此，VP最大值或最小值对应的测线方位难以准确地指示裂缝走向。

α在测线方位角为0°或180°时达到最小值，在测线方位角为60°和240°出现极小值，在测线方位角为120°和300°时达到最大值(图8b)。因此，α最小值对应的测线方位可准确地指示裂缝走向，α最大值对应的测线方位判定裂缝走向存在一定偏差。随着d增加，α基本呈双峰值分布，均在测线方位角为180°附近出现波谷。这是因为尽管在某些测线方位角声波绕射通过裂缝到达接收端的路程较短，但裂缝严重阻挡了声波能量传播，即使VP较大，α也较大。本文对随机离散裂缝模型纵波方位各向异性特征的数值模拟结果表明，VP不一定在测线方位角为0°或180°时出现最大值，也不一定在90°或270°时出现最小值。因此，只有α最小值对应的测线方位才可较准确地指示裂缝走向。本文进一步深化了杨勤勇等[8]有关裂缝介质的纵波方位各向异性特征的认识。

为了分析各向异性的差异，参考Thomsen[20]分析纵波各向异性程度的方法，定义VP相对变化量ΔVP和α相对变化量Δα表征各向异性程度

(3)

(4)

式中下标max、min分别代表对应变量的极大值、极小值。由式(3)、式(4)得到模型8的ΔVP和Δα分别为0.20和0.81，即Δα≫ΔVP，因此衰减各向异性特征较速度各向异性特征更显著。

图12、图13分别为ΔVP、Δα随d的变化。由图可见, ΔVP随d的变化规律不明显(图12)， Δα随d增加而减小(图13)。造成上述现象的原因为：VP还受裂缝空间分布位置的影响，因此ΔVP与d不存在明显的相关关系；当孔隙度φ一定时，随着d增加，由裂缝条数较少的大裂缝转变为裂缝条数众多的细小裂缝，空间分布逐渐均匀，各向异性特征减小，因此Δα随d增加而减小。杨勤勇[21]选用4种厚度的有机玻璃片制作不同裂缝密度的均匀裂缝岩心模型进行物理模型实验，结果表明，随着裂缝密度减小，测线方位角为0°和90°时的反射时差逐渐增大，即纵波方位各向异性随测线方位角增大逐渐增大。本文对随机离散裂缝模型纵波方位各向异性特征的数值模拟结果不支持文献[21]的认识。

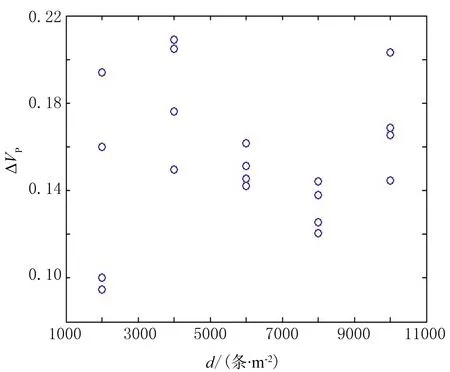
图12 ΔVP随d的变化

3.2 裂缝流体对方位各向异性特征的影响

图14为裂缝模型，图15、图16分别为VP、α随测线方位角的变化曲线。由模拟结果可见： 当测线方位角为0°或180°时，裂缝及充填流体对声波首φ=4%，θ=30°，d=4800条/m2，r均值为20。裂缝中流体为气/水两相，裂缝内孔隙流体的含水饱和度分别为15%、30%、45%、60%、75%、90%、95%和100%波影响很小，因此不同饱和度间的VP(图15)和α(图16)的变化差异很小；当测线方位角较大时，裂缝严重阻挡声波首波传播，因此不同饱和度间的VP(图15)和α(图16)的变化差异明显。

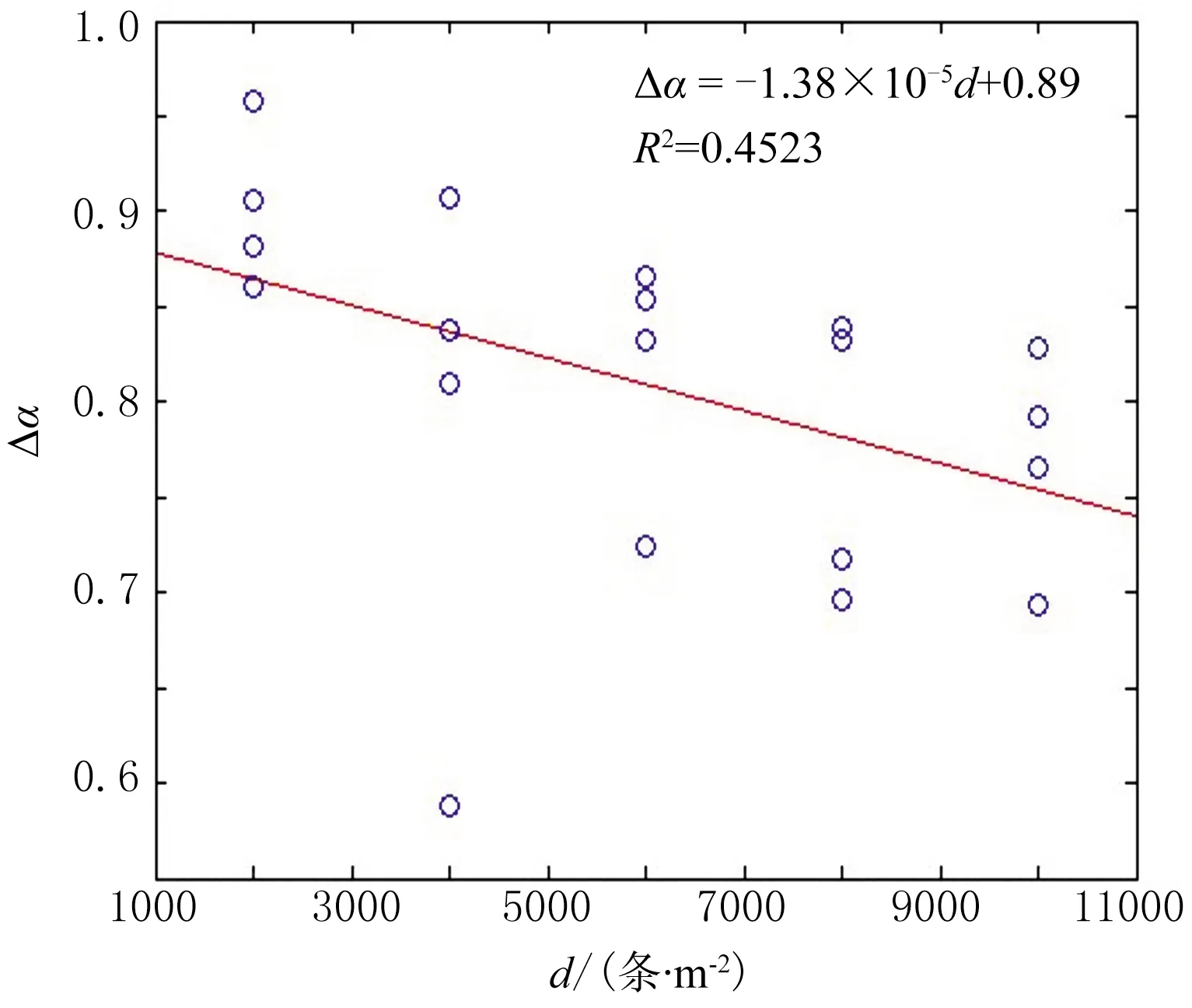
图13 Δα随d的变化R为相关系数

图14 裂缝模型

图15 VP随测线方位角的变化曲线

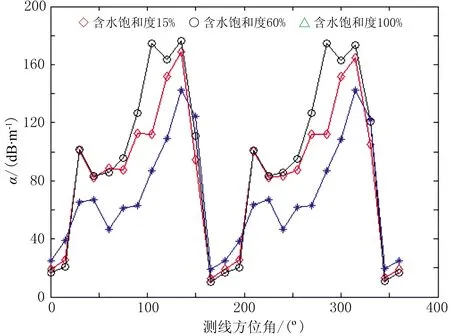
图16 α随测线方位角的变化曲线

图17、图18分别为测线方位角为90°或270°时VP、α随含水饱和度的变化曲线。由图可见：①当含水饱和度较小时，随着含水饱和度增加，VP先减小并出现最低值(图17)，α逐渐增大并出现最大值(图18)，这与气/水两相孔隙流体的微观分布模式有关[22]；随着含水饱和度进一步增加，VP逐渐增大(图17)，α逐渐减小(图18)。②当含水饱和度高于90%时，VP迅速增大(图17)，α迅速减小(图18)。这是因为随着含水饱和度增加，声波透射能量增强，声波透射通过裂缝的时间越短，透射波对首波初至的影响也越明显，导致VP增加、α减小。

图19、图20分别为ΔVP、Δα随含水饱和度的变化曲线。由图可见，随着含水饱和度增加，ΔVP、Δα均先增大后减小。由于当测线方位角为0°或180°时VP、α的变化很小，因此ΔVP和Δα主要由测线方位角较大时VP和α的变化决定。由图15可见，含水饱和度分别为15%、60%、100%的VP最大值几乎相同，不同含水饱和度的VP最小值先减小后增加，因此ΔVP先增大后减小。同理，由图16可见，含水饱和度分别为15%、60%、100%的α最小值几乎相同，不同含水饱和度的α最大值先增加后减小，因此Δα先增大后减小。

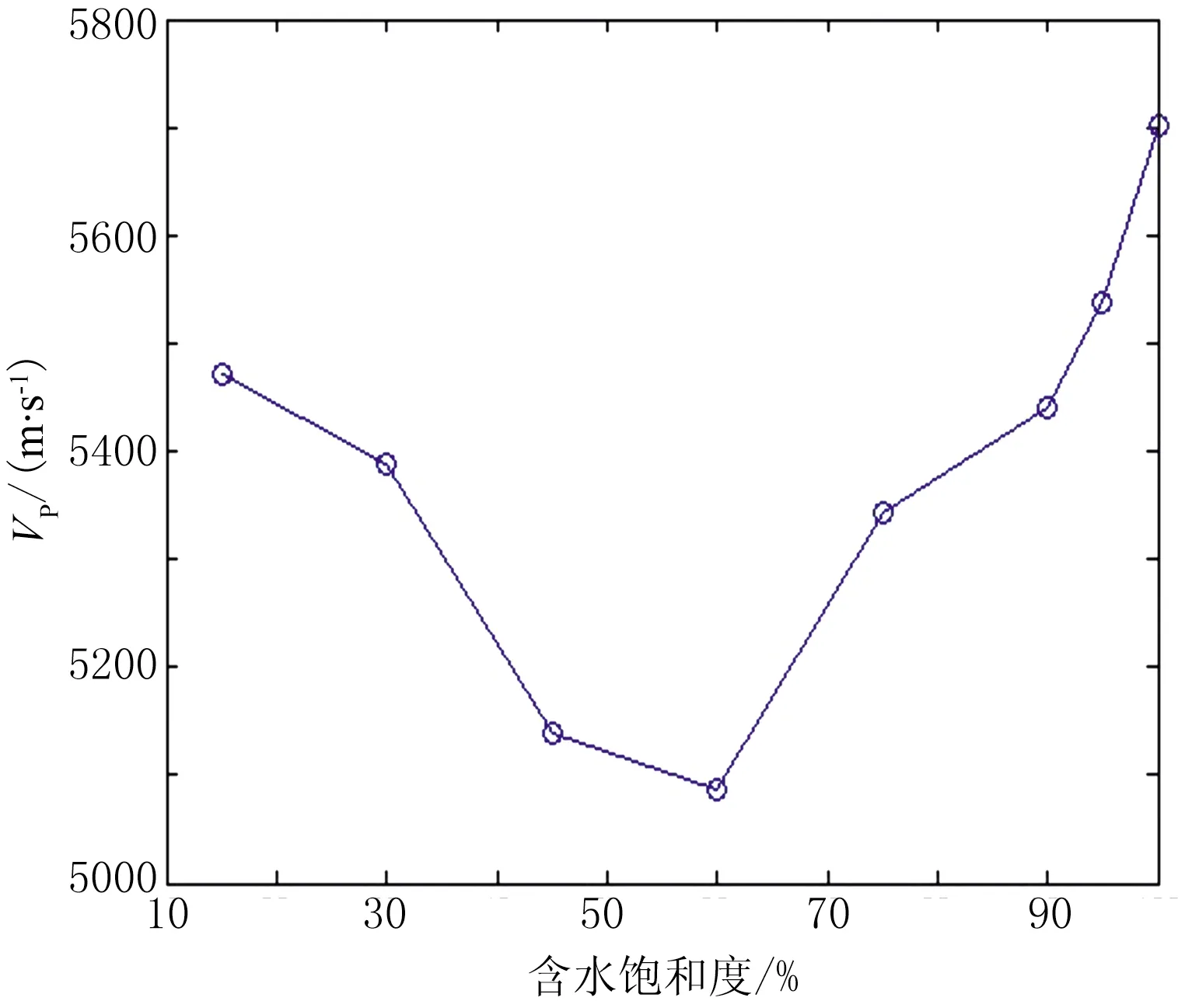
图17 测线方位角为90°或270°时VP随含水饱和度的变化曲线

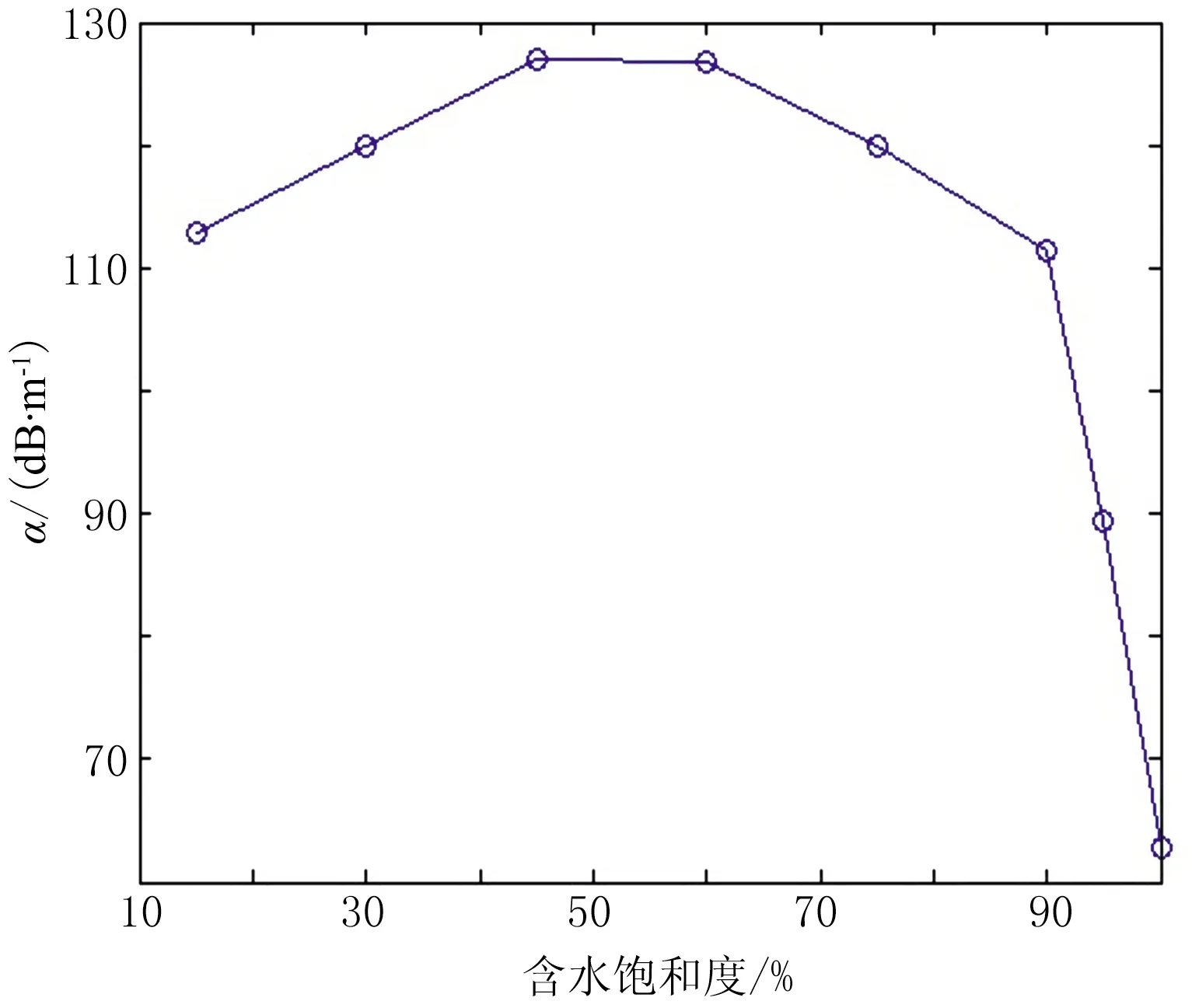
图18 测线方位角为90°或270°时α随含水饱和度的变化曲线

图19 ΔVP随含水饱和度的变化曲线

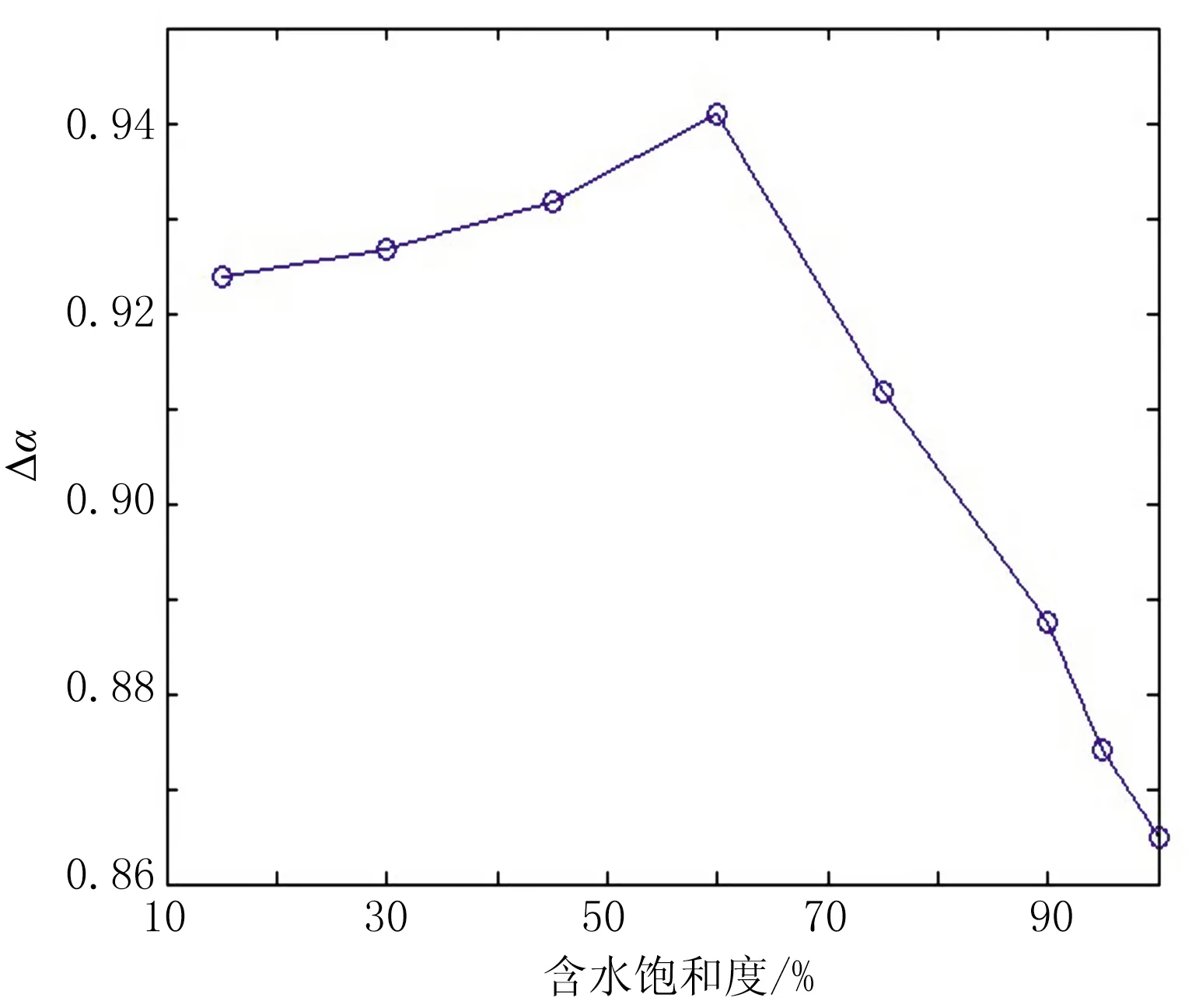
图20 Δα随含水饱和度的变化曲线

丁拼搏等[23]在不同饱和流体条件下利用超声波透射法测试含裂缝分布的岩样，结果表明，岩样在饱气条件下的纵波各向异性系数远高于岩样饱水。受基质渗透性和裂缝分布状态的影响，实验中往往难以控制裂缝流体的部分饱和分布状态，本文的数值模拟结果支持丁拼搏等的实验结果，还讨论了气/水两相部分饱和状态下随机离散裂缝模型的纵波各向异性特征，并进一步总结了纵波速度和衰减系数相对变化量随含水饱和度的变化规律。

4 结论

本文对随机离散裂缝模型的声波波场的数值模拟结果表明：裂缝参数变化对声波衰减系数的影响远远大于对声波速度的影响，采用声波衰减系数最小值对应的测线方位可较准确地判定裂缝走向；随着裂缝密度增加，衰减系数相对变化量减小；随着含水饱和度增加，速度和衰减系数的相对变化量均先增大后减小。上述认识为利用声学参数检测裂缝提供了理论基础。