基于人工地标的移动机器人定位与调整技术*

李俊杰，黄 翔，李泷杲，曾 琪，主 逵

（1.南京航空航天大学机电学院，南京 210016；2.深圳市劲拓自动化有限公司，深圳 518126）

激光跟踪仪、激光雷达等测量设备具有测量精度高、测量稳定性好、测量速度快等优点，目前在航空航天领域已经得到普遍应用[1]。由于被测飞机构件尺寸较大或者结构复杂，测量设备在使用过程中往往需要转站才能实现对盲区的测量[2]，随着移动机器人技术日趋成熟，使用移动机器人搭载测量设备的自动化转站技术有效避免了人工干预转站过程中测量效率低、过程繁琐的问题。为保证自动化转站过程中测量设备在测量站位点的位姿误差在允许范围内，需要通过移动机器人的导航定位技术保证移动机器人到达精确的测量站位点。导航定位技术一直是移动机器人领域的重点研究内容，与目前移动机器人常用的惯性导航、磁带导航等方式相比，人工地标的视觉导航具有定位精度高、没有累计误差、对环境要求较低、设备性价比高等优点，近年来在国内外得到了越来越多的研究与应用[3–5]。

黄璐等[6]将人工路标分为纠偏人工路标和定位人工路标，虽然都具有良好识别率，但将编码信息和位姿信息分离，信息量过少，降低了实用性。Chae 等[7]使用红外路标来进行机器人的定位，该路标被固定于天花板上，对光照条件不敏感，但是对其进行识别时需要使用带有红外带通滤波器的CCD 摄像机。霍亮等[8]提出了一种视觉路标快速识别方法，当图像发生严重畸变时依然能够快速有效地识别，试验取得了很好的效果。高飞等[9]提出一种基于位置判别的激光QR 码定位方法，当探测图形不完整时仍可有效地进行精确定位,具有很高的可靠性。但上述两种方法均存在地标图像复杂、解码算法繁琐的现象，容易造成解码难度大的问题。

针对上述问题，本文设计了一种新型的人工地标，图案简单易于识别，携带编码信息和位姿信息，并可通过标定工装实现在全局坐标系下标定。在自动化转站过程中，移动机器人通过识别人工地标并进行编码与位姿解算，根据相应的调整策略，实现定位与姿态调整。最后，通过试验验证移动机器人满足到达指定目标点的精度要求。

1 系统描述

1.1 系统工作流程

测量设备的自动化转站过程见图1，测量设备在当前站位完成测量工作后，移动机器人搬运测量设备到达下一测量站位点附近，通过单目相机采集人工路标进行定位与位姿调整，保证测量设备在新的测量站位点满足位姿精度要求，测量设备在新的测量站位点继续测量工作，测量完成后再由移动机器人搬运至下一站位，直至完成全部测量工作。

图1 自动化转站Fig.1 Automated station-transfer

移动机器人在测量站位点通过人工路标进行定位与位姿调整的具体流程如图2所示。在转站工作开始前，首先将地标布置在规划好的测量站位处，并利用标定工装对人工地标在全局坐标系下进行标定，建立人工地标的编码与测量站位坐标的人工地标索引库。当测量设备在当前站位完成测量工作后，由移动机器人搬运至下一站位，到达新测量站位附近后，用搭载的相机对人工地标进行图像采集并预处理。对预处理后的人工地标进行识别，若识别成功，对人工地标进行编码及位姿解算，经过坐标转换可知移动机器人当前位姿与目标位姿的旋转矩阵与平移向量，并将结果作为驱动量控制移动机器人调整位姿；若识别未成功，则根据预设信息驱动移动机器人调整姿态后重新采集图像。调整完成后，判断移动机器人位姿与目标位姿是否在允许的误差范围内，若仍不满足则跳到图像采集再次进行上述工作循环调整，若满足则表明移动机器人成功到达目标位姿点，移动机器人便放下激光跟踪仪，在新站位开始测量工作。

1.2 坐标系标定

移动机器人定位与调整系统，包括移动机器人坐标系{D}、相机坐标系{C}、人工地标坐标系{M}和全局坐标系{W}，如图3所示。其中，移动机器人的坐标系建立在它的几何中心，单目相机安装在移动机器人上，且为减少图像畸变影响，需保证单目相机光轴和地面近似垂直。相机坐标系建立在光轴中心处，其Z轴与光轴中心线方向一致，以相机到地标的方向为正方向，其X轴方向则取图像坐标沿水平增加的方向。

人工地标布置于地面上，其位姿由激光跟踪仪测量站位规划时确定，并经过地标标定工装标定，根据齐次坐标转换原理，地标坐标系{M}与全局坐标系{W}的转换关系WMT为已知。

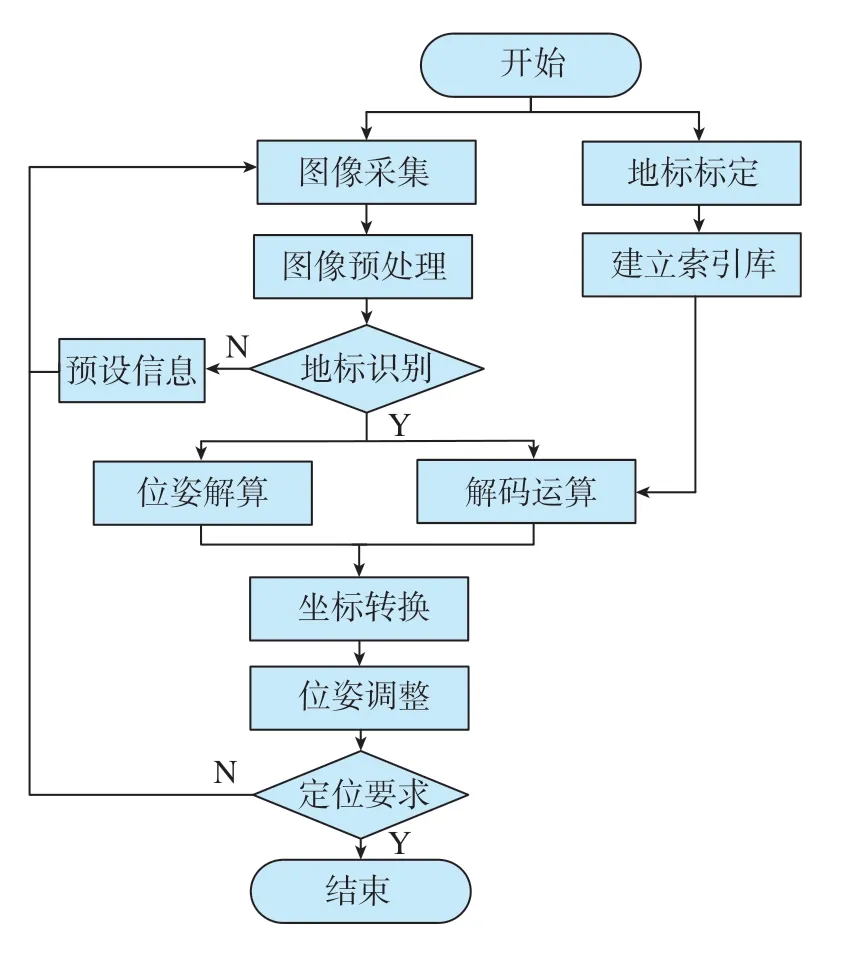
图2 移动机器人定位与调整流程Fig.2 Mobile robot positioning and adjustment workflow

其中，WMR为旋转矩阵，Mt为平移向量，即WMT综合表示了旋转矩阵和平移向量。相机安装位置由移动机器人的结构决定，移动机器人坐标系{D}与相机坐标系{C}的位姿关系同样可由旋转矩阵和平移矩阵进行变换，即CDT为已知。

因此，计算出相机坐标系{C}与人工地标坐标系{M}的转换关系WCT，便可由CDT、MCT、WMT通过坐标转换确定移动机器人坐标系{D}在全局坐标系{W}下的位姿，实现移动机器人定位：

2 人工地标设计及其标定方法

2.1 人工地标设计

设计一种黑白两色的圆形人工地标，可分为最外层黑白相间的环形色块组成的编码区和内部的5 个黑色位姿特征点组成的数据区，图4展示了其中两个人工地标。

编码区是每个地标具有唯一性的标识，为移动机器人提供编码信息。如图5（a）所示，编码区的黑色和白色色块分别代表了二进制中的0 和1。色块的数量根据地标的实际使用数量需求确定，本文使用了8个色块，代表8位二进制数，因此最多可以代表256 个不同的地标。

数据区为移动机器人提供位姿信息。如图5（b）所示，数据区的5 个黑色位姿特征点的排列规则为：竖直方向的3 个特征点在地标竖直方向的对称线上，其中中间的特征点位于地标中心；水平方向的两个点的圆心分别位于竖直方向对称线的两侧，其圆心的连线与竖直方向3 个特征点圆心连线垂直。

2.2 标定工装设计及标定方法

为了在激光跟踪仪自动转站前快速准确地标定人工地标的位姿，即确定地标坐标系{M}与全局坐标系{W}的变换关系，根据三角定位的思想，设计了一种等边三角形的人工地标标定工装，如图6所示。

如图7所示，在进行标定时，将所要标定的人工地标放置于标定工装中间，用激光跟踪仪的靶球放置在标定工装的3 个安装位置上，3 个安装位置在地标坐标系{M}下的坐标已知，记为PM1，PM2，PM3，PMi=（xmi，ymi，zmi）T（i= 1，2，3），利用激光跟踪仪测量3 个靶球，可以得到3 个点在全局坐标系下的坐标，记为PW1，PW2，PW3，由坐标转换关系，可以得到下式：

变换矩阵的求解方法主要有最小二乘法[10]、SVD分解法[11]和四元数法[12]，此处利用四元数法求得人工地标在全局坐标系下的WMT，完成人工地标的标定工作。标定完成后，根据标定结果建立人工地标索引库，使每个地标的编码与其在全局坐标系下的位姿一一对应，储存在地标索引库中，当移动机器人获取到地标的编码值时，则在索引库中搜索匹配即可得到该地标的全局坐标系下的位姿信息。

图3 系统坐标系标定Fig.3 Calibration of system coordinate

图4 人工地标设计Fig.4 Design of artificial landmark

图5 地标功能区域划分Fig.5 Division of landmark functional area

3 基于人工地标的定位与调整原理

3.1 图像预处理

在飞机构件测量的环境中，地板通常存在一些干扰杂点，为提高图像识别准确率，需要进行图像预处理，包括对采集的图像进行灰度化处理、均值滤波去噪，对去噪后的图像进行阈值分割，获得二值图像，最后对二值图像进行开运算和闭运算，以消除图像中出现的纤细点及小型黑洞。

二值化处理的关键是阈值的选择，为保证二值化图像效果，采用最大类间方差法来确定阈值[13]。最大类间方差法是一种自适应的阈值确定方法，首先将0～255依次设为阈值，遍历每一个像素值，根据阈值把图像分为背景物与前景物。记ω1、ω2分别为背景、前景像素点占整幅图像的比例，μ1、μ2为背景、前景的平均灰度值，类间方差σB通过下式计算：

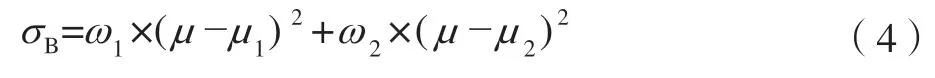
其中，

当类间方差σB最大时，前景和背景差异也最大，对应的阈值即为所求，用以图像分割可以得到区分最明显的二值化图像，

3.2 地标特征识别

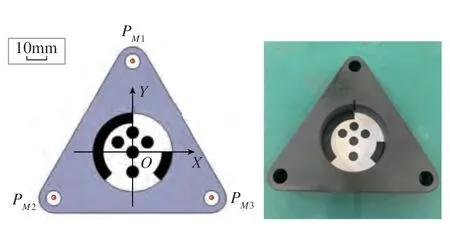
图6 地标标定工装Fig.6 Landmark calibration tooling

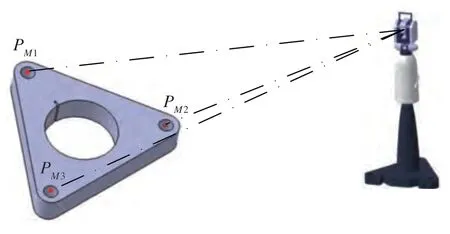
图7 人工地标标定方法Fig.7 Method of artificial landmark calibration

对预处理后的图像进行边缘检测，其中检测到的边缘以树形结构存储，根据面积约束、圆度约束、颜色约束和凸度约束，过滤掉多余的轮廓，目的是找到候选位姿特征点的轮廓。

将经过约束过滤后剩下的轮廓作为候选位姿特征点的轮廓，利用轮廓的特征矩计算其质心坐标，即得到候选位姿特征点的圆心。对每2 个不同的候选位姿特征点进行排列组合，遍历每对组合，计算每对组合的组成直线的参数。去除组合直线的两点后，找出候选位姿特征点中的剩余点，分别计算剩余点与直线的距离，若小于设定的阈值，则判断为内点。用最小二乘法对两点与内点进行直线拟合，找到与直线距离的最小的内点，则保存此时的两点及内点，将此3 个点作为位姿特征点。找出候选点中剩余两点，将这两点用最小二乘法拟合直线，求出两条直线的交点，记为点B，如图8所示。

接下来对先找到的3 个点重新排序，排除距离最远的两个点，中间点为点C。判断剩余两点与交点B的距离，距离近的记为点A，另一个记为点D。由于图像中直线的交比与地标设计的所定的交比相比保持不变，与相机位姿无关，基于这一特点对人工地标进行识别。

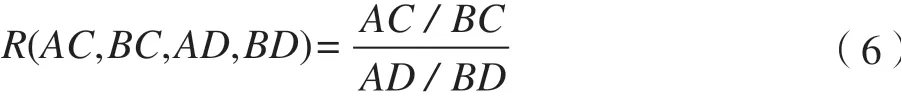
由点A、C、D及交点B的坐标，计算交比R（AC，BC，AD，BD）的值与图标设计时所定的交比值的偏差是否在设定的范围内。当偏差在设定范围内时，将剩余两点排序，以点D到点A为正方向时，左侧的点记为点E，右侧的点记为点F。

3.3 编码与位姿解算

通过图像识别，已知点A、D、E、F的图像坐标，图标设计时该4 点在图标坐标系下的坐标也已知，可利用该4 点进行透视变换，将图标转正。以点D到点A为正方向时，顺时针依次按每个色块所占的角度依次统计该色块区域内的黑色像素和白色像素，将黑色像素的色块判定为0，将白色像素的色块判定为1，得到1个8 位二进制数，转化为相应的十进制数，即这个地标代表的编码值。

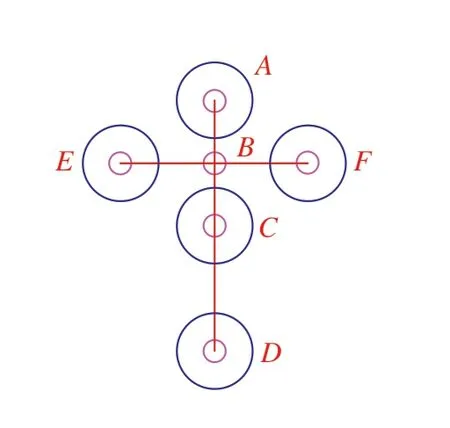
图8 特征点识别Fig.8 Feature point recognition

相机的内参采用四参数模型已经预先完成标定，4个位姿特征点A、D、E、F在地标坐标系中的坐标已知，它们的图像坐标也已经得到，因此求MCT的问题可以转换成共面P4P 线性求解问题[14]。首先由4 个位姿特征点的图像坐标（ui，vi）计算出在相机的焦距归一化成像平面的成像点P1ci坐标：

将位姿特征点在地标坐标系中的坐标Pdi代入摄像机的外参数模型：

联立上面两式可得：

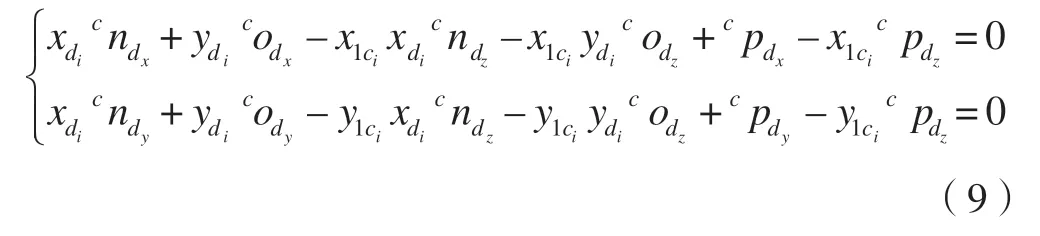
由4 个已知位姿控制点，可以得到4 组式（9）所示的方程，即8 个方程，解方程组即可得到相机坐标系{C}与人工地标坐标系{M}变换的旋转矩阵和平移向量MCT。

4 试验及结果分析

4.1 移动机器人调姿策略

试验采用图9所示的移动机器人作为试验平台，该试验平台为两轮差速控制，主机基本配置为intel I7–4560U，并采用100 万像素相机采集图像，可以满足大部分的视觉任务要求。

由于相机与移动机器人的位置固定，为叙述方便，将移动机器人坐标系与地标坐标系视作移动机器人坐标系，如图10所示。为提高精度采用循环调整的策略，其中每一次调整分为3 个步骤，具体如下：

（1）根据前文，可计算出移动机器人坐标系Y轴正方向与地标坐标系原点的夹角α（α<180°），移动机器人按照夹角的方向旋转α，使其面向地标坐标系原点。

（2）移动机器人前进L，使移动机器人坐标系与地标坐标系原点重合。

（3）计算此时移动机器人坐标系Y轴正方向与地标坐标系Y轴正方向的夹角θ（θ<180°），按照夹角的方向旋转θ，本次调整完成。

4.2 地标位姿解算精度试验

试验的目的是验证本文设计的人工地标位姿解算的精度，分为位置精度和角度精度两部分试验，试验过程如图11所示。试验时，首先分别将两块地标标定，将标定的位姿值作为实际位姿值。然后，遮挡一块地标，相机采集图像并计算位姿，再遮挡另一块地标，再次采集图像并计算位姿，便可根据两次采集得到的结果计算两块地标之间的距离和角度。

图9 试验平台Fig.9 Experiment platform

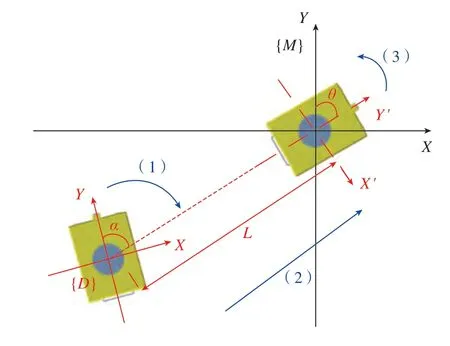
图10 移动机器人调整策略Fig.10 Mobile robot adjustment strategy

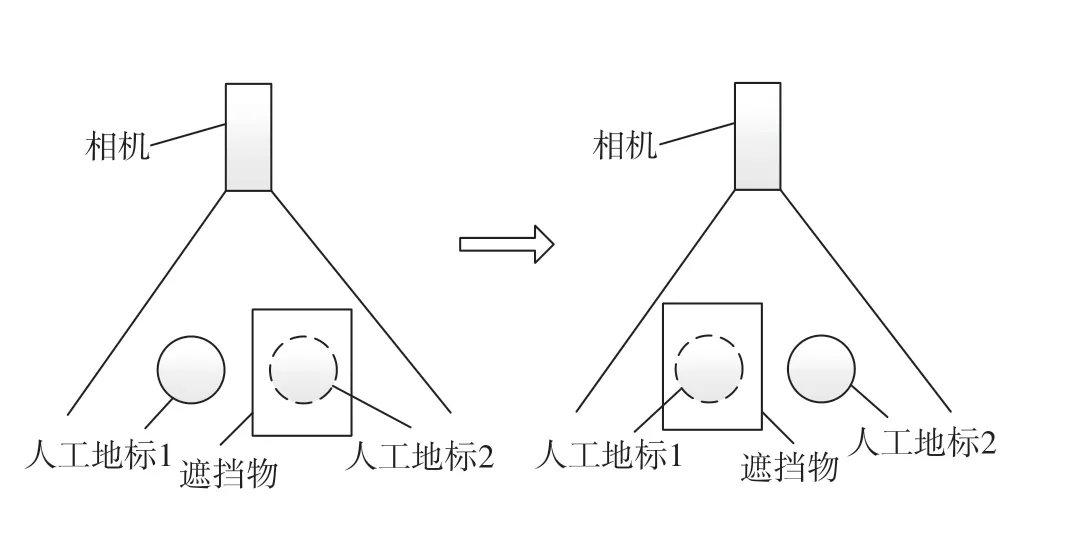
图11 试验过程示意图Fig.11 Diagram of experimental process

验证位置精度时，根据相机视场范围大小，以50mm 为间隔设置6 组不同距离的两块地标；验证角度精度时，根据机器人实际的旋转角度范围，以30°为间隔设置7 组不同角度的地标，每组试验测试50 次并采用结果的平均值作为两块地标的距离或角度测量值。计算测量值与实际值的差值，试验结果如表1和表2所示。

通过试验得到的位置误差和角度误差均较小，其中，当测量距离超过250mm 时位置误差明显增大，这是因为距离较远时地标不可避免地出现在图像的边缘，受图像畸变影响而导致误差增加。但本文采用的是循环调整的策略使移动机器人不断调整逼近目标位姿，调整过程中地标越来越趋近于图像中心，图像受畸变影响会随着调整过程的继续而减少，从而得以保证调整的精度，因此图像畸变问题对位姿调整影响有限。

4.3 移动机器人姿态调整试验

对移动机器人姿态调整进行试验，目的是为了验证机器人姿态调整的精度。试验时，将人工地标设置在地面上，放置移动机器人在任意的不同位置，同时必须保证人工坐标在机器人搭载的相机视野范围内，然后进行图像采集、解算以及调整运动。由于移动机器人的运动精度有限，因此加入一组移动机器人经过运动精度补偿后的数据作为对比。补偿的方法是发出控制指令使移动机器人移动一段距离或角度，使用激光跟踪仪测量其实际运动的距离或角度，经过多次试验得到目标值和实际值的近似线性关系，对控制指令加上相应补偿使其实际运动的距离或角度达到目标值，以提高移动机器人的运动精度。

将移动机器人调整后相机位姿与地标位姿的接近程度作为移动机器人的调整精度，包含位置精度和角度精度两部分。记录经过一次调整后的调整精度、经过循环调整后的调整精度和补偿后移动机器人经过循环调整后的调整精度，试验结果如图12所示。

由图12可知，循环调整比只进行一次调整的精度更高，表明该策略有助于提高机器人的调整精度，同时，随着补偿后移动机器人运动精度的提高，其调整精度也比补偿前得到了明显提高。通过多次试验结果可知，经过一次调整后的调整精度为12.89mm、9.76°，经过循环调整后的调整精度为10.36mm、3.98°，补偿后的循环调整后的调整精度为7.58mm、2.39°，补偿后经过循环调整的调整精度基本满足调整精度的要求。

表1 位置误差Table 1 Position error mm

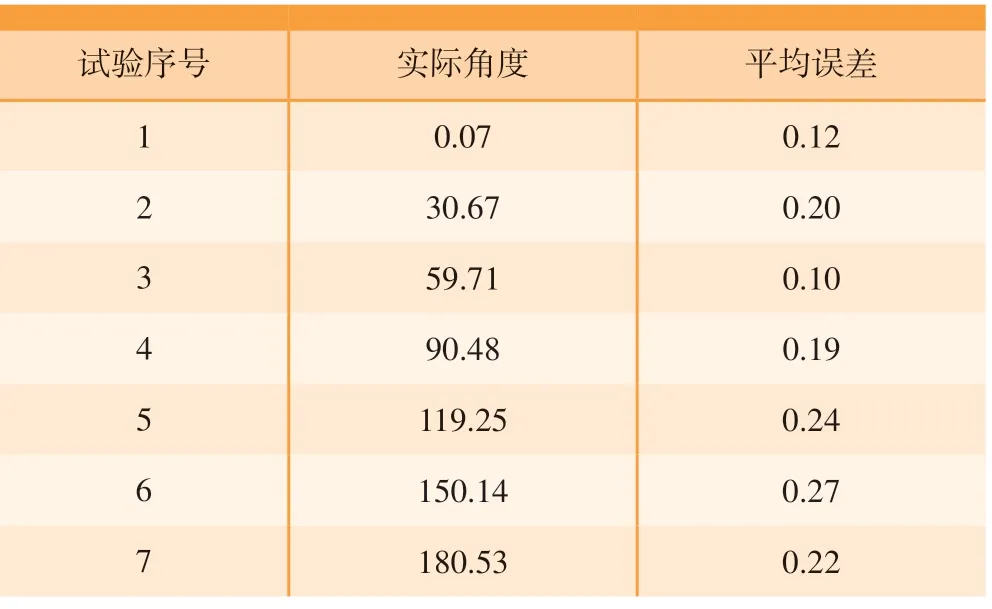
表2 角度误差Table 2 Angle error （°）

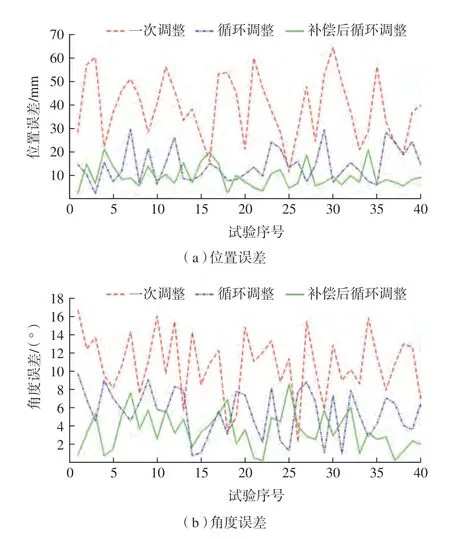
图12 调整后的误差结果Fig.12 Error result after adjusting

5 结论

在飞机大型构件测量领域，针对测量设备的自动化转站存在无法准确到达目标站位点的问题，提出了采用基于人工地标的移动机器人定位与调整技术实现转站时的精确定位。

（1）设计了一种人工地标及其识别与解算的方法，相应设计了地标标定工装及标定方法，可以利用激光跟踪仪实现快速准确地获得地标在全局坐标系下的坐标。试验表明，通过该人工地标计算的位置误差和角度误差均较小，满足移动机器人调姿的需要。

（2）设计了移动机器人的位姿调整策略，通过试验表明，调整后的偏差值的均值为7.58mm，满足自动化转站的精度要求，因此本文提供的基于人工地标的移动机器人定位与调整技术具有一定的应用价值。

由于调整的误差值来源主要包括车体运动精度、车轮与地面的打滑情况、相机光轴与地面不垂直、图像畸变等因素，因此，在今后的研究中优化上述因素可以进一步提高调整精度。