先进复合材料VARTM工艺树脂流动数值模拟研究

李 晨，黄 甲，陈 程，高丽敏

（1.中国商飞北京民用飞机技术研究中心民用飞机结构与复合材料北京市重点实验室，北京 102211；2.上海理工大学机械工程学院，上海 200093）

先进复合材料由于具备比模量和比强度高、耐腐蚀性能和抗疲劳性能好、设计和制造一体化成型等诸多优点，而被广泛应用于航空、航天、交通运输、能源和建筑等行业[1]。当前，先进复合材料已由最初作为产品次承力部件和内饰材料逐步发展成为主承力部件的材料，但复合材料较高的使用成本在一定层面上限制了其在工业领域的大规模应用。复合材料制品的成本主要来自原材料和制造工艺两部分，其中制造工艺方面的成本占到70%左右[2]。

作为一种典型的先进复合材料低成本成型工艺，复合材料液体成型技术（Liquid Composites Molding，LCM）因具有生产效率高、制件表面光洁度好、尺寸精度高、闭模成型环境污染小的诸多优点得到越来越多的关注。VARTM 工艺作为液体成型工艺中较常见的方法，近年来已被广泛应用于工业生产制造。例如，俄罗斯MC21 支线客机和庞巴迪C 系列飞机都将液体成型技术用于飞机机翼制造[3]。图1[4]为一个典型的VARTM工艺。

传统的对VARTM 工艺进行优化的方法往往需要依靠经验并通过大量试验对树脂流动情况进行预测。这种方法需要耗费大量人员精力、资源和材料，拉长研制周期。而采用基于流体力学方程的有限元数值模拟方法对模具内树脂流动过程进行模拟可以有效降低VARTM 工艺设计成本，有利于优化工艺参数，从而提高产品开发效率。国外有很多学者对此展开研究，Drapier[5]和Blais 等[6]利用Darcy 定理耦合Stokes 方程的方法研究了树脂在预成型体内外的单相不饱和流动情况，但是在数值收敛性上仍然存在很多问题。Gantois 等[7–8]采用边界元的方法在宏观部件尺度上模拟树脂流动进行了比较，虽然计算速度较快但是只对边界预测精度较低。近年来，国内学者也针对RTM 工艺仿真开展了广泛研究[9–11]，杨波[12]、Li 等[13]采用有限元方法对树脂流动和缺陷在微观和细观层面进行了预测，但没有探讨宏观尺度情况；戴福洪等[14]采用控制体积和等效渗透系数方法模拟边缘效应，以避免干斑工艺缺陷的产生，然而控制体积方法计算精度较差，影响了预报结果。目前，国内采用有限元方法对树脂单相（不含空气相）流动的VARTM 工艺树脂浸润过程进行的研究相对较少，在宏观尺度上模拟的主要控制方程还是Darcy 定理，对树脂流动前沿轮廓一般采用水平集或控制体积等传统方法。本文采用理查德方程作为流动控制方程，应用一种轮廓函数描述树脂瞬时流动前沿，基于COMSOL Multiphysics 多物理场仿真软件的偏微分方程（Partial Differential Equation，PDE）模块，通过有限元方法实现了对树脂充模过程中树脂流动前沿和流场压强的预报，并将该方法得到的数值仿真结果与所设计的试验进行对比，证明了该方法的正确性。

1 数值模拟方法

对树脂流动进行数值模拟的过程可以归属为计算流体力学（Computational Fluid Dynamics，CFD）的范畴，一个完整的计算流体力学过程如图2所示。

控制方程是整个计算过程的核心，是对物理过程的公式化表述；初始值和边界条件规定了物理过程的起始情况和边际范围；对计算域的网格划分、方程和初始条件边界条件的离散是有限元的基础，通过循环求解以达到数值结果满足收敛条件。

1.1 控制方程

为满足公式的使用条件，需要进行如下假设：

（1）纤维预成型体为连续的多孔介质结构，并且在树脂浸润过程中不会发生形变。

（2）树脂在纤维预成型体中的流动为多孔介质渗流并满足达西流动特性。

（3）树脂的流动为恒温流动，充模过程中树脂黏度保持恒定，且忽略树脂的化学反应。

1.1.1 渗流方程Darcy定理

Darcy 定理：

其中，称=–为 达·西ΔP速度（m/s），表示平均体速度；μ是树脂的黏度（Pa·s）；P为压强（Pa）；K代表多孔介质纤维增强材料的渗透率张量（m2）。K为二阶张量，对于笛卡尔坐标系下的二维多孔介质材料的渗透率张量可以表示为：

三维渗透率张量可表示为：

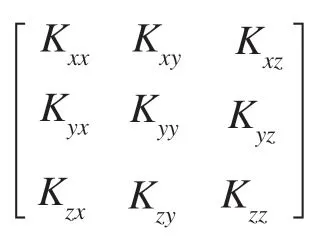
1.1.2 质量守恒定律

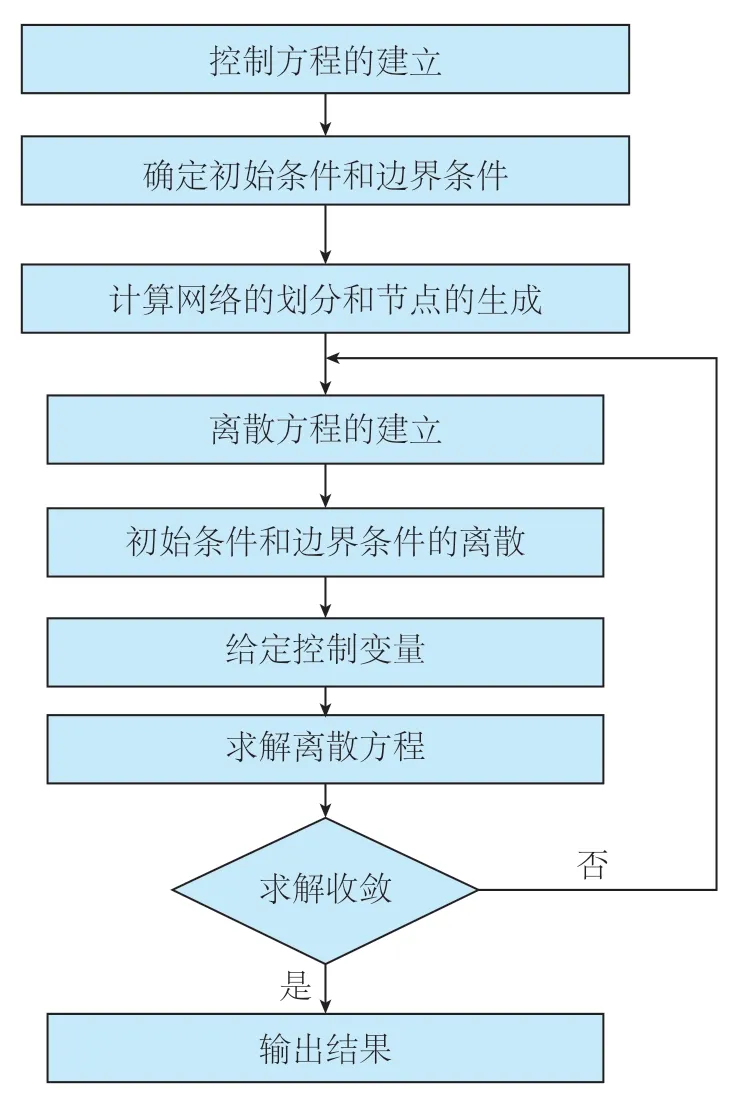
图2 计算流体力学过程Fig.2 Process of computational fluid dynamics

质量守恒定律或称连续性方程，是任何流体流动过程中需要遵守的普遍性方程。其中，ρ表示流体密度；v是速度向量；ε表示多孔介质的预成型体的孔隙率。

当式（2）中流体流动达到稳态平衡时，流体不可被压缩，此时为常数，式（2）可化简为：

1.1.3 理查德方程（Richard方程）

将经典Darcy 方程（式（1））代入式（2），同时引入无量纲的饱和度变量S∈[0,1]，可得到式（4）即为简化的Richard 方程。

1.2 轮廓方程

理查德方程建立了瞬时条件下的饱和度S和压强P之间的关系。对树脂流动前沿的轮廓描述，本文采用Kojima 等[15]提出的轮廓方程，如式（5）所示，它通过建立S（P）方程确立了变量压强P和饱和度S的直接关系。这里α定义为数值形状因子（1/Pa），不同α选取值对饱和度S和压强P关系的影响如图3所示。

从图3可知，随α升高数值模拟的收敛性逐渐升高，综合考虑数值模拟的收敛性、饱和度S和压强P计算的准确性，本文选取α=0.001。将式（5）运用链式法则进行变换可得式（6）。这样式（4）就转化为关于压强P与时间t的方程。

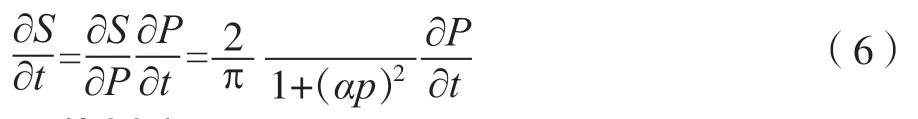
1.3 网格划分

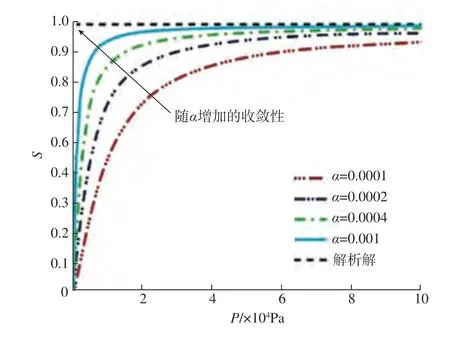
图3 考虑变化的饱和度S和压强P关系Fig.3 Relation of S and P considering variation of α

合理的网格划分是后续采用有限元方法高效计算的基础，在COMSOL Multiphysic 软件中，PDE 方程采用Galerkin 方法[16]进行离散。在采用CFD 进行分析和边界层网格划分过程中，将控制方程离散到基函数上时，三角形单元和四边形单元是最常用的两种线性网格单元类型，如图4所示。

为验证本文方法的正确性，建立了一个几何结构模型（图5），在矩形区域内预设了两个小矩形区域阻碍树脂流动，在临近下端的位置预设阻碍区域与整个矩形边缘区域相联通。采用三角形单元对几何模型进行有限元划分后的结果如图5（b）所示，共包含5760 个域单元和270 个边界单元。

图5 几何结构模型Fig.5 Geometrical model

1.4 边界条件和初始值

如图5所示，除了两个位于几何模型中部的注入口，其他边界条件均设为不可渗透。

模拟开始前，模具内压强与出口压强都为0；树脂开始注入时，入口压强(Pin)和出口压强(Pout)的初始值分别为1×105Pa 和0。

2 试验设计和参数设定

试验设备由树脂灌注系统和位于树脂灌注系统上部的检测系统两部分构成。树脂灌注系统由密封铺放在柔性真空袋内的单层编织纤维布、导管和真空泵组成；检测系统由CCD（Camera Coupled Device）相机构成，负责记录试验中不同时刻树脂流动前沿的位置，试验装置如图6所示。

试验和数值模拟选用的材料参数值如表1所示，纤维预成型体的渗透率沿水平方向（Kh）和竖直方向（Kv）各异。

3 结果对比验证

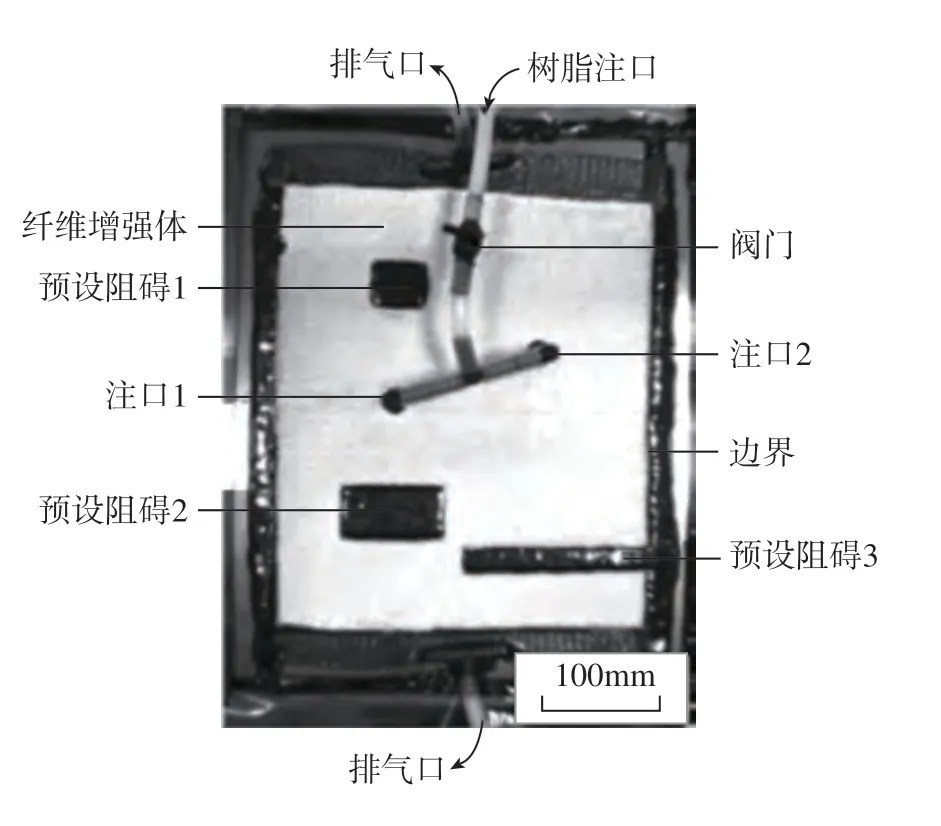
图6 试验设计Fig.6 Experiment design

表1 材料参数Table 1 Material parameters

在不同时刻，树脂流动前沿位置和压力场的试验结果和数值模拟结果如图7所示，其中图7（a）、（e）、（i）、（m）为不同时刻试验所得树脂流动前沿的记录；图7（c）、（g）、（k）、（o）为文献[8]中采用边界元法获得的压强场结果；图7（b）、（f）、（j）、（n）和图7（d）、（h）、（l）、（p）分别为采用本文方法所获得的树脂流动前沿和压强场的结果。

为了更直观准确地量化对比试验和数值模拟得到的树脂流动前沿结果，本文定义浸润比（λ），λ=S树脂/S纤维，其中S树脂代表对应时刻下平面内树脂流过区域面积；S纤维代表整个纤维铺放区域的面积。不同时刻模拟值和试验值获得的浸润比（λ）如图8所示。试验和数值模拟的差异可以理解为，数值模拟中只考虑树脂的单相流体流动，不包含空气气体相对流动的阻碍。而在实际试验中树脂灌注初始阶段，由于真空袋密封区域内还有部分空气未排出，且残余空气没有均匀分布在纤维预成型体内，所以树脂流动初始阶段试验获得的浸润比λ试验<λ模拟；而伴随树脂灌注继续进行，空气逐渐被排出密封区域，树脂流动加快，则λ试验>λ模拟。

不同时刻数值模拟与试验的λ绝对值差，即|λ试验–λ模拟|小于10%，具有良好的准确性。将不同时刻压强场结果的极值与文献中结果进行了对比，亦得到近似结果。本文方法在与文献[7]中所列相似的硬件平台上运行相同案例和相近计算规模时，计算时间仅为57s，远低于该文献中采用边界元法计算的200s，这证明了本方法在计算效率上的优越性。因此，可以得出本文所用数值模拟方法对压强和数值流动前沿的预报都较为准确，证明了该方法的正确性。

4 结论

本文基于理查德方程和一种轮廓函数，利用COMSOL Multiphysics 多物理场仿真软件，实现了对树脂浸润纤维预成型体过程的数值模拟预测。预测结果经与试验结果相比较，证明该方法具有准确的预报结果。

本文所实现的方法，目前仅用于二维模型的流动仿真，由于实际生产制造中许多复材部件具有一定的厚度尺寸，因此在后续研究中可以探索将该方法扩展到三维尺度模型上。其次，本文中所用的纤维增强材料的渗透率数值为材料本身标定，在后续研究中可以探究基于本文建立的宏观尺度方法，将基于数值模拟对细观结构进行分析获得的渗透率数值迭代入本文方法中，进行多尺度渗流研究。同时，温度变化对流体流动特性的影响诸如树脂黏度变化等，也可以纳入后续数值模拟的研究范围。

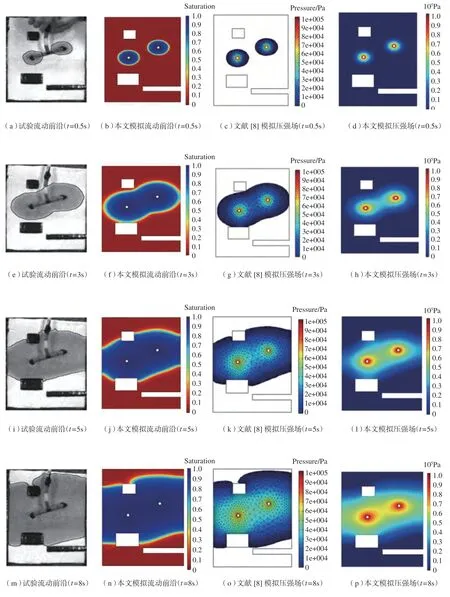
图7 验证结果对比Fig.7 Comparison of results

图8 不同时刻浸润比模拟值和试验值Fig.8 Infusion ratio λ of results from simulation and experiments at variant time