基于SIEMENS数控系统的机床综合误差实时补偿方法研究*

肖 晓，张 聘，魏亚飞，汪 建，连成哲，叶文华

（1.航空工业济南特种结构研究所，济南 250023；2.南京航空航天大学机电学院，南京 210016）

误差补偿技术可以有效且经济地提高数控机床的加工精度[1]。数控机床的误差补偿通常可分为以下步骤[2]：误差源的分析和检测、误差数学模型的建立、误差元素的辨识和建模、误差计算与补偿。其中，误差补偿是通过刀具或工件在空间误差的逆方向产生一定的位移实现，是误差补偿技术的最终环节。

误差实时补偿方法主要分为反馈中断法和原点平移法[3]。反馈中断法的实现是将误差的相位信号插入伺服系统的反馈环中，但插入相位信号比较复杂，所以该方法使用较少。原点平移法将误差补偿值发送至CNC 控制器，在加工过程中实时地将控制系统的参考原点向误差反向平移，因其不影响坐标值和加工程序的优点，获得了大量使用。如吴昊[4]针对双主轴立式车床AC–300，以外接计算机为处理器搭建软硬件平台，通过I/O 口将误差补偿值发送至数控系统CNC 控制器，实现切削力误差的实时补偿；姜辉[5]针对FANUC 0i 数控系统，自行研制的基于单片机的误差补偿器，与CNC 系统进行实时数据交互，基于外部坐标原点偏移功能实现机床几何误差与热误差的实时补偿；胡胜海等[6]针对数控火焰切割机提出一种在线修正加工误差的实时补偿方法，根据加工误差综合预测模型，建立动态补偿策略，在原有加工过程中较小干扰的前提下进行补偿运动。

虽然误差实时补偿技术受到越来越多学者的重视，对各类误差研究有了很大的进步，但依然存在没有充分利用现代数控系统本身的功能、需要开发专用补偿器、开发难度大、通用性差等问题。

本文针对SIEMENS 840D 数控系统，在深入研究数控系统本身具有的误差补偿方法的基础上，利用温度补偿功能，结合BP 神经网络，提出了一种能对力误差、热误差等误差进行综合补偿的实时补偿方法，仅需在PLC 中加入少量程序，可在不影响机床正常运行的前提下实现误差补偿，并利用自行开发的误差补偿平台验证该方法的有效性。

基于SIEMENS 数控系统的机床误差实时补偿方法

1 数控机床误差实时补偿的一般方法

数控机床误差实时补偿一般采用基于半闭环反馈的补偿方式，其原理如图1所示。在加工过程中，通过对一些能表征机床当前加工状态、环境变化的参量如温度、切削力、加工位置、加工参数等进行监测，建立机床加工误差与这些变量之间的关系，按误差模型实时计算当前条件下的误差值，并以一定手段进行误差补偿。

误差实时补偿方法中，反馈中断法是将相位信号插入伺服回路，这种方法实现起来比较复杂，且容易对机床造成不可预料的影响。原点偏移法不需要对机床进行复杂的操作，只需要在PLC 中添加少量程序便可实现，目前西门子、发那科等主流数控系统都提供了用原点偏移法进行热误差补偿的功能接口。本文对西门子840D 数控系统进行了综合误差实时补偿技术研究。

2 SIEMENS 数控系统的温度补偿功能

SIEMENS 的某些高端数控系统（如840D、840D sl 等）针对由环境温度变化、切削热传导、运动部件生热等因素引起的机床部件热变形误差提供了温度补偿功能[7]。对于每一个轴来说，在一定温度下，热误差与位置的曲线可表示如下：

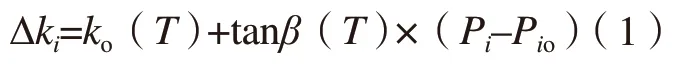
式中，Pi是i轴的当前位置，其中i表示坐标轴，如X、Y、Z轴；Po是i轴上热误差测量的参考点；ko（T）是参考点在温度T下的误差值；tanβ是温度补偿系数。

该功能通过测得的当前温度值按照温度误差曲线实时计算误差值并在插补中进行补偿。但由于上述温度误差值的计算方法过于简单，热误差的计算值与实际值差异较大，难以实现高精度的热误差补偿。

3 基于SIEMENS 数控系统温度补偿

功能的综合误差实时补偿方法

对式（1）表示的热误差计算式，SIEMENS 数控系统还提供了进一步简化计算的方法：

此时，数控系统中生效的补偿值等于变量ko（T）的值。

因此，如果将外部误差模型计算得到的误差补偿值实时写入该变量，即可实现机床误差的实时补偿。不仅可实现热误差的补偿，还可以实现包括力误差和其他误差在内的机床误差综合补偿。基于SIEMENS 数控系统温度补偿功能的综合误差实时补偿原理如图2所示。

目前，国内外已有大量关于机床误差模型的研究[8]，包括三角函数模型、矢量模型、二次模型、变分模型、基于运动链的模型、多项式回归模型、神经网络模型等。但上述这些模型大部分只适用于几何误差、热误差等单项误差建模。机床误差主要包括几何误差、热误差、切削力误差。由于机床加工过程中情况复杂，各类误差相互耦合，要建立准确的机床单项误差模型是十分困难的。考虑到式（2）的误差补偿值是一个综合误差补偿值，因此，本文通过建立综合误差模型来计算综合误差补偿值。

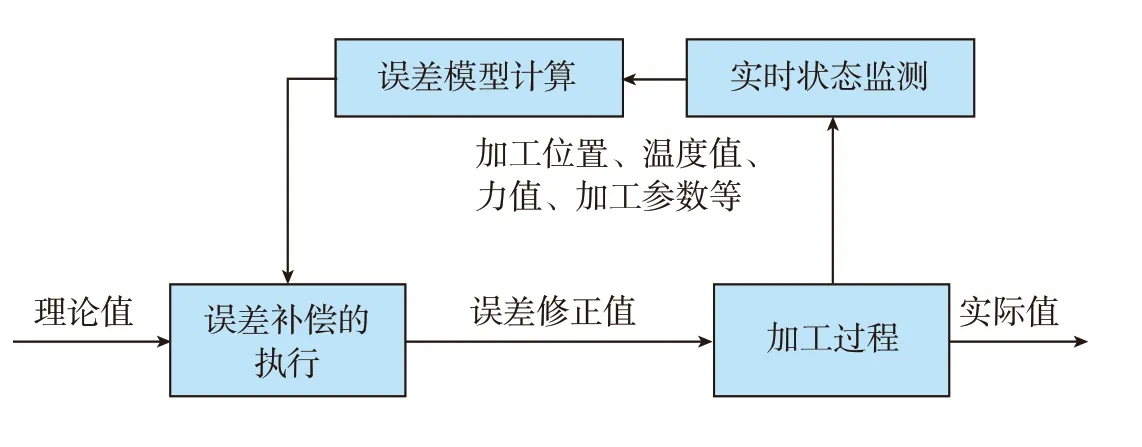
图1 误差实时补偿原理Fig.1 Principle of error real-time compensation

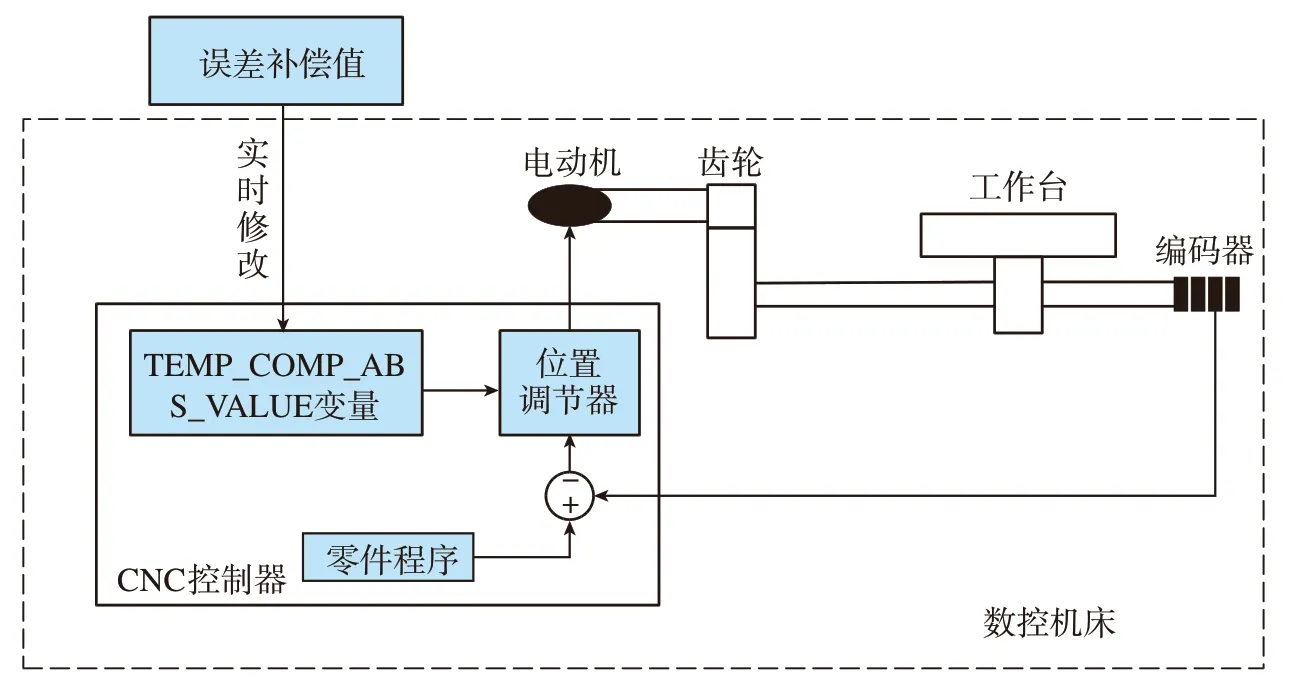
图2 基于温度补偿功能的实时补偿原理Fig.2 Real-time compensation principle based on temperature compensation

由于神经网络具有很强的非线性映射能力和自适应能力[9]，可以通过学习提取样本中的规律建立输入与输出之间的关系，很容易建立机床加工参数与误差之间的模型。由于单隐层BP 神经网络几乎可以用来拟合所有的非线性函数关系[10]，因此本文采用单隐层BP 神经网络建立机床综合误差模型。其神经网络模型的结构如图3所示。

基于BP 神经网络建立机床综合误差模型，首先需要确定神经网络的输入参数，要求参数可以直接或间接反映出当前加工位置的实际误差。参考国内外对于各类机床误差模型的研究结果[11–13]，本文确定几何误差相关的输入参数为机床各轴的位置坐标，热误差相关的输入参数主要为机床关键温度测点，切削力误差相关的输入参数为主轴负载、主轴转速、切削进给量、切削深度。机床综合误差模型所有输入相关参数见图4，神经网络模型的输出为加工过程中机床各个进给轴的综合误差补偿值。补偿值不仅包含进给轴的丝杠热膨胀、机床导轨滑块热变形等热误差和机床导轨移动中产生的几何误差，还包括因切削力引起的进给机构变形而产生的加工误差。

综合误差实时补偿系统开发

ARM（Advanced RISC Machines）是目前在工控领域得到广泛应用的微处理器，基于ARM 的嵌入式系统不仅具有较强的数据处理能力，同时也可以搭载不同的嵌入式操作系统，并能提供友好的人机交互。因此本文采用ARM 嵌入式系统作为平台，设计开发了机床误差实时补偿系统，在采集机床参数时建立了ARM 和数控系统PLC 的Modbus 通信，通过这种方式可以方便地将补偿值发送给数控系统PLC。综合误差实时补偿系统结构如图5所示。

采用符合机床温升范围的温度传感器对机床加工过程中关键点温度变化进行实时监测[13]。机床加工参数如主轴转速、切削深度、主轴负载、各轴位置坐标等可以通过ARM 与PLC 建立的Modbus 通信进行读取。

软件开发在Qt Creator 的集成开发环境中完成，主要实现机床加工过程中温度变化监测、机床加工参数监测、基于神经网络的综合误差模型计算、补偿值发送等功能。程序流程图如图6所示。

为了计算补偿周期，计算了补偿系统在上述配置下误差模型的计算时间为18.41ms。同时，综合考虑采集硬件和补偿值写入PLC 后机床执行零点偏置所需的延时时间在8ms 左右，所以最终确定补偿周期为30ms。

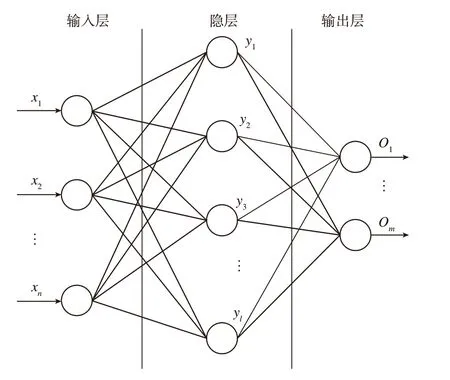
图3 机床综合误差的神经网络模型结构Fig.3 Neural network model structure of comprehensive machine error

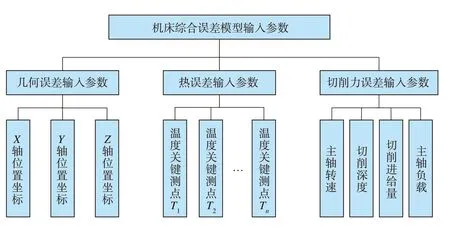
图4 机床综合误差模型输入参数Fig.4 Input parameters of comprehensive machine error model

试验验证

以图7所示的基于SIEMENS 840D 数控系统加工中心为试验平台，以图8所示的铝合金6061 试件为切削加工对象进行综合误差补偿试验。验证试验分两步进行，第1 步为神经网络模型训练与验证，第2 步为实时误差补偿试验。试件上设计了左右对称的两组壁厚为2mm 的薄壁曲面，其中第1 组左曲面用于神经网络模型训练，第1 组右曲面用于神经网络模型验证；第2 组左曲面加工时进行实时误差补偿，第2 组右曲面加工时不进行误差补偿，用于对比。左右两组曲面的切削条件相同，分别为切深1mm、进给量200mm/min、转速3000r/min。

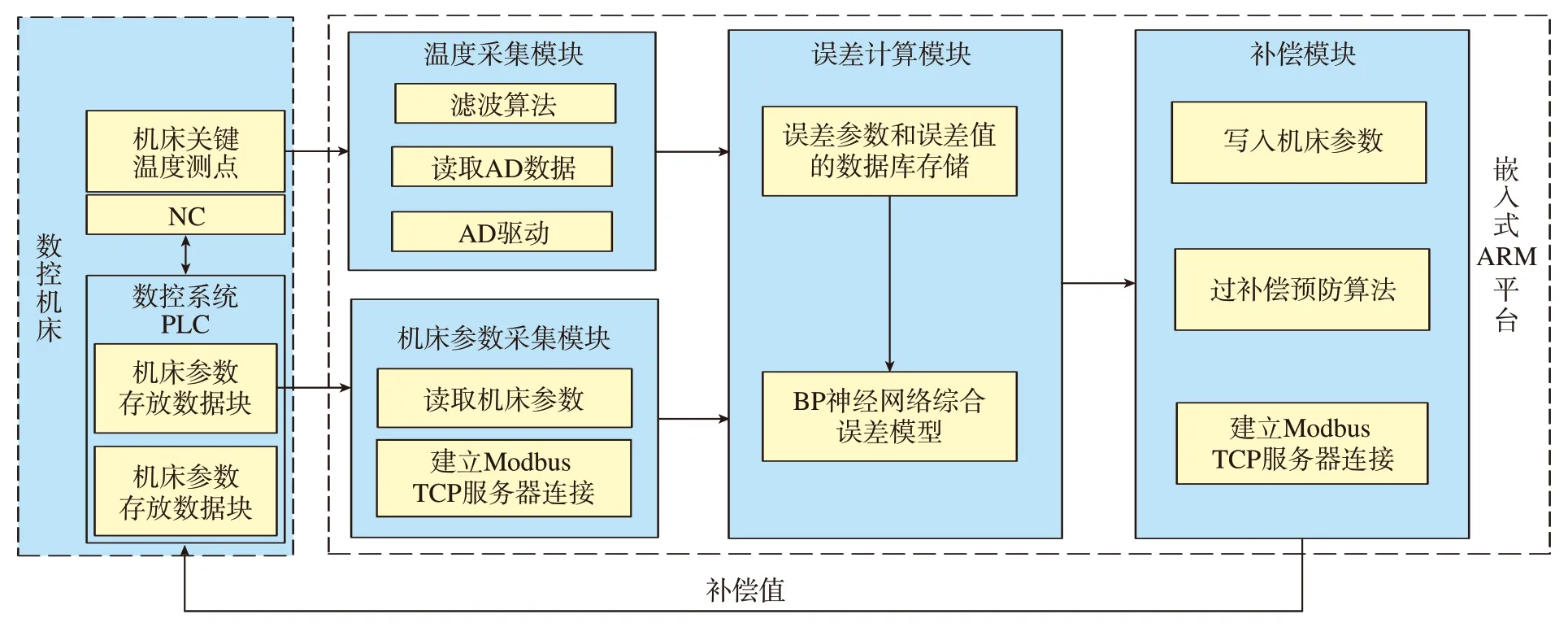
图5 综合误差实时补偿系统总体结构Fig.5 Overall structure of comprehensive error real-time compensation system

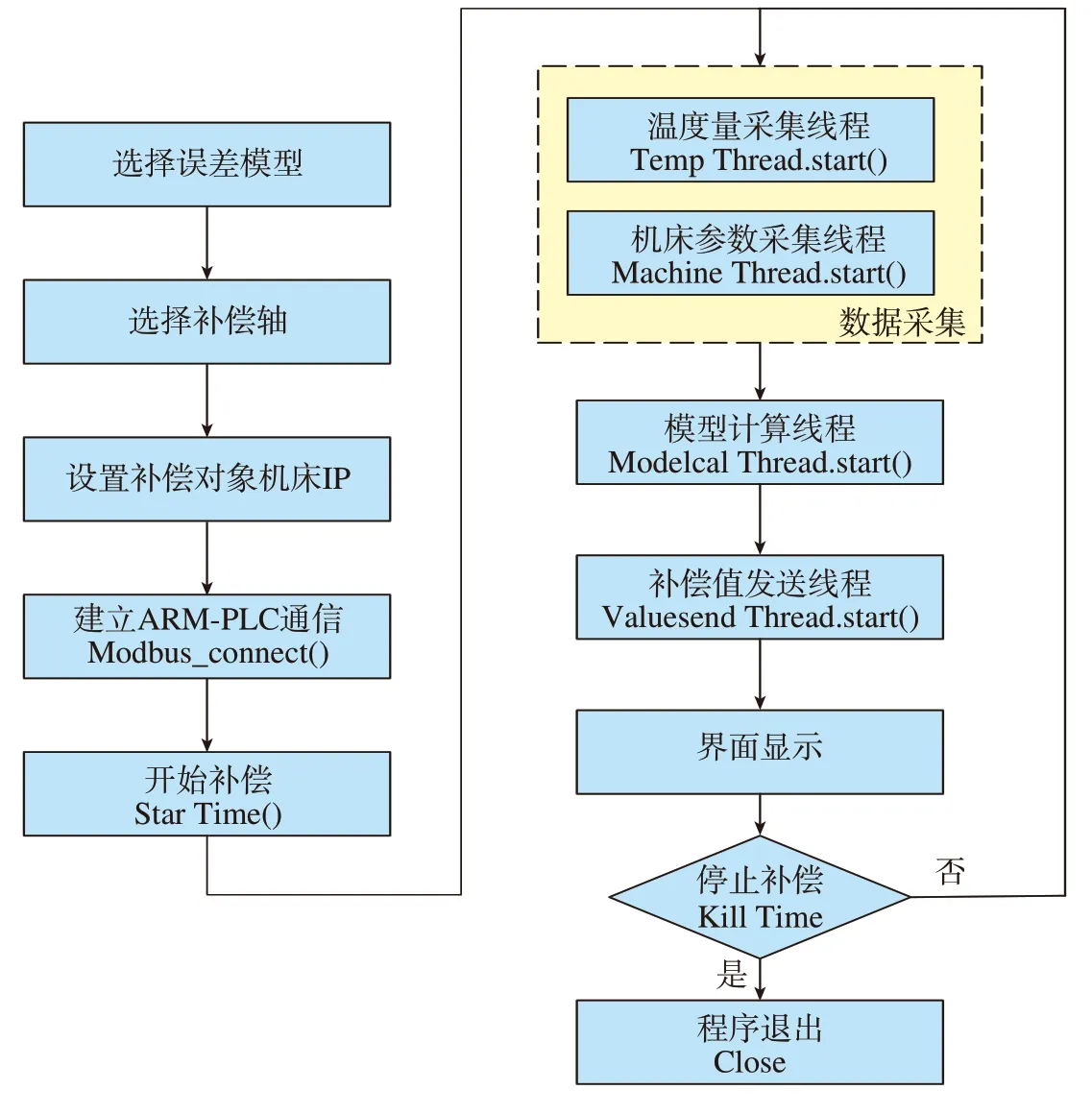
图6 误差实时补偿系统程序开发流程Fig.6 Program development flow of real-time error compensation system

图7 SIEMENS 840D数控加工中心Fig.7 SIEMENS 840D CNC machine center

图8 试件模型与试件Fig.8 Test part and its model

首先进行神经网络模型训练与验证试验。模型中几何误差与力误差有关的输入参数与图4相同。热误差有关的输入参数为温度关键测点，温度关键测点可按一般热误差建模中的方法来确定。本文基于课题组以前对该机床温度场研究，采用模糊聚类分析与灰色关联度相结合的方法来确定机床温度关键测点，即优化选取对热误差影响较大的温度变量，然后对这些温度变量进行分类，最后在各类测点中选取具有代表性的测点作为热误差建模所用的温度变量。最终确定每个移动轴进给机构的4 个关键温度测点，分别位于螺母、轴承座、电机和导轨上。机床温度传感器布置示意图如图9所示。模型输出为曲面测得的X、Y、Z方向的误差值。按上述切削条件对试件第1 组左右2 个曲面分别进行加工，并用在线测量系统对2 个曲面各取100 个测点进行测量。100 个测点分成X方向均布的10 组，每组又分成Z方向均布的10 个测点，见图10。最后用左曲面的数据来训练BP 神经网络，右曲面的数据用于神经网络模型验证。试验结果证明模型是有效的。

然后基于上面建立的神经网络模型进行综合误差实时补偿试验。按上述切削条件对试件第2 组左右2 个曲面分别进行加工，并在加工左曲面时进行综合误差实时补偿。加工后同样用在线测量系统对2 个曲面各取100 个测点进行测量，2 个曲面的Y向误差如图11所示。

通过测量结果可见，右曲面Y向峰值最大误差为175.13μm，补偿误差后左曲面Y向峰值最大误差为71.66μm，最大误差减小了59.1%，验证了本文所提出的误差实时补偿方法的有效性。

鉴于零件加工误差涉及机床、刀具、工件等众多因素，本文方法中考虑的因素相对比较简单，尚不能满足实际应用需要。

结论

本文介绍了数控机床误差实时补偿一般方法。根据SIEMENS 数控系统提供的温度补偿功能，结合基于BP 神经网络的综合误差模型，提出了一种机床综合误差实时补偿方法，并以ARM 嵌入式为平台开发了综合误差实时补偿系统。

图9 温度传感器布置示意图Fig.9 Schematic diagram of temperature sensor arrangement

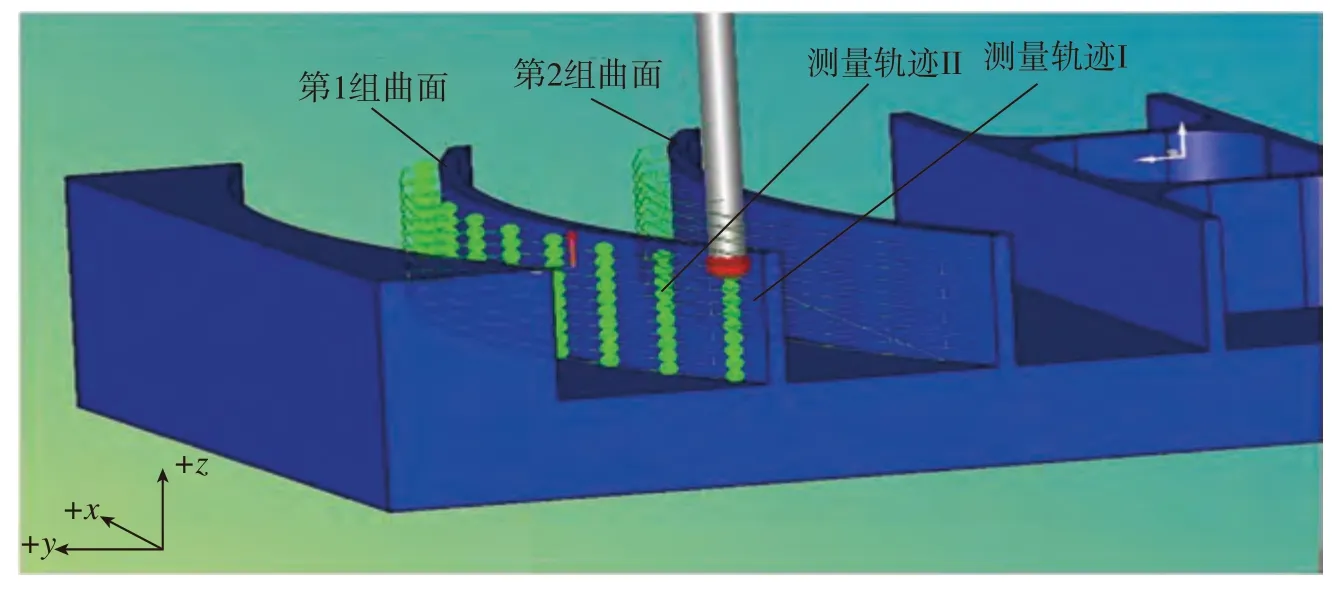
图10 曲面测点位置Fig.10 Surface measuring point

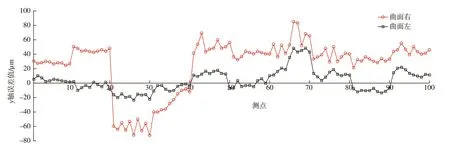
图11 第2组曲面左、右两边的Y 向误差值对比Fig.11 Comparison of Y-direction error values of left and right sides of two sets of surfaces

以西门子840D 数控系统机床为试验对象，对铝合金6061 试件进行切削加工，并在加工过程中利用开发的综合误差实时补偿系统进行机床综合误差实时补偿，与误差未补偿时相比，试件最大误差减小59.1%，验证了本文所提出的补偿方法的有效性。