转盘干燥机转子圆盘拉撑件径向适宜位置分析
史为帅 董金善 李 川 刘林波 胡国呈
(南京工业大学机械与动力工程学院)
因转盘干燥机具有热效率高、蒸发强度大及节能环保等特点[1],被广泛应用于干燥各种粘糊状、粉状及粒状等热敏性较稳定的有机物和无机物料[2]。转盘干燥机的基本工作原理为:在干燥机身内,中空轴上焊接的空心加热圆盘作为转子缓慢旋转,蒸汽由转子空心轴的一端进入,通过圆盘壁面间接加热干燥机身内的物料[3,4],圆盘外侧设置带有倾角的耙叶,用于翻抄、搅拌物料[5]。
转盘干燥机的核心部件为主轴上的转子圆盘, 而受拉撑的圆盘与加筋的平盖结构类似,大多学者对加筋平盖进行了研究:许留关和薛绛颖分析了加筋平盖的应力分布,得出了加强筋的存在使得平盖上高应力趋于平缓,设备整体力学性能显著提高[6];贺小华等应用有限元方法分析了烘缸加筋平盖结构的受力[7];冯永利等提出了以平行角钢为加强筋的圆形平盖应力的理论计算方法[8];谭志洪等通过理论分析与有限元计算结合,加强筋的存在有效降低了平盖与筒体连接处由 于 刚 度 差 引 起 的 应 力 集 中[9,10];谢 志 刚 等 应 用有限元分析软件ANSYS对平盖加筋结构进行了优化设计,效果显著[11,12]。
受拉撑转子圆盘虽然与加筋平盖类似,但是由于圆盘结构的特殊性(锥角的存在)使得拉撑件只能沿着圆盘环向布置,而拉撑件径向位置的合理设置,是圆盘整体结构强度设计的关键。 为此, 笔者以单圈拉撑圆盘和两圈拉撑圆盘为例,采用有限元法探讨了拉撑件在不同径向位置下对圆盘结构应力分布的影响,同时考查圆盘锥角α(上下两盘片内壁面所形成的角度)和宽节比Lw/Lc(圆盘径向宽度Lw与拉撑件周向节距Lc之比)的影响,详细分析单圈、两圈拉撑圆盘拉撑件的最佳径向位置,从而为转子圆盘的结构设计提供参考。
1 单圈拉撑圆盘的拉撑件径向适宜位置分析
1.1 单圈拉撑转子圆盘模型结构尺寸的确定
依据GB 150—2011《压力容器》[13]中最大无拉撑区域计算盘片厚度的思路,内压一定时圆盘厚度由最大无拉撑区域决定。 当单圈拉撑时,拉撑件应尽可能处于圆盘径向的中央使无拉撑区域尽可能减小, 为此选取L1/Lw分别为0.35、0.40、0.45、0.50、0.55、0.60、0.65这7个位置进行详细研究,同时考虑圆盘锥角α对最佳拉撑位置的影响,分别取α为8、12、16、20°这4个水平分析模型,盘片有效厚度T1=8mm,拉撑件厚度t=5mm,单圈拉撑转子圆盘模型结构参数如下:
轴管D2×T2377mm×25mm
圆盘直径D11 000mm
拉撑件d×t 32mm×5mm
拉撑件的周向节距Lc185mm
盘片有效厚度T18mm
1.2 单圈拉撑转子圆盘位移变形分析
图1给出圆盘锥角α=8°时, 不同拉撑位置下单圈拉撑圆盘典型拉撑截面(放大40倍)的位移变形, 图中虚线部分为圆盘初始时的结构形状。由变形结果可以看出盘片被拉撑件分割为多个区域,各区域中心有明显的“鼓胀”,对比7个位置的位移变形,随着拉撑件位置L1远离中心轴管,盘片最大位移变形先减小后变大,相应的最大位移点由拉撑件与外端焊缝之间逐步转移至拉撑件与轴管所围成区域之间,符合最大无拉撑区域大小的变换规律。
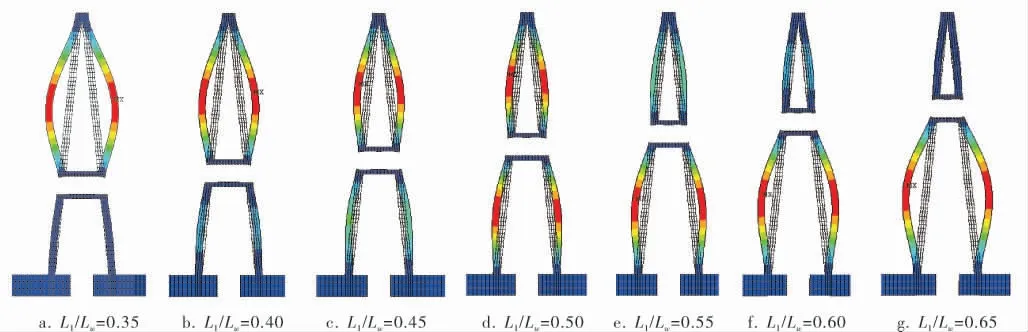
图1 α=8°时不同拉撑位置下典型拉撑截面变形
图2为不同拉撑位置下单圈拉撑圆盘最大位移变形值,虚线左侧表示最大变形发生在拉撑件外侧, 虚线右侧表示最大变形发生在拉撑件内侧。 图2表明,随着拉撑位置L1/Lw逐步增大,最大变形逐渐减小,当拉撑件位于圆盘正中央时变形最小;拉撑位置L1/Lw继续增大,变形开始增大,但此时增大的幅度要小于距圆盘中心相同距离靠近轴管时的衰减幅度, 随着拉撑位置的改变,最大位移并未沿圆盘中央位置对称分布,L1/Lw=0.60时的最大变形比L1/Lw=0.45时的最大变形还要小;同时,当拉撑位置L1/Lw≥0.60时,“鼓胀”相连在一起,变形区域相互连成一片,各个区域最大变形几近相同,此时拉撑件的设置未能显著抑制圆盘的变形, 整个圆盘形成了一整圈等大的最大变形。 对比不同圆盘锥角下不同拉撑位置的单圈拉撑转子圆盘最大变形,可以发现锥角对最大变形的影响仅在L1/Lw≥0.55与L1/Lw≤0.40时才逐步显现,圆盘最大变形随着圆盘锥角的增大而略微减小。

图2 不同拉撑位置下单圈拉撑转子圆盘最大位移变形
1.3 不同锥角α下单圈拉撑圆盘应力分析
由于转子圆盘最大应力点均出现在盘片与拉撑件的拉撑截面处, 依据JB/T 4732—1995(R2005)《钢制压力容器——分析设计标准》[14]中应力分类方法,提取拉撑截面处的局部薄膜应力强度SII和一次+二次应力强度SIV, 图3为不同圆盘锥角α下单圈拉撑圆盘应力随不同拉撑位置的变化规律。

图3 不同拉撑位置下单圈拉撑转子圆盘应力分布规律
图中拉撑截面的局部薄膜应力强度SII和一次+二次应力强度SIV随拉撑位置的增大先减小后增大,在L1/Lw=0.50附近达到最小值,并且关于L1/Lw=0.50几乎呈对称分布,表明拉撑件位于圆盘中央时圆盘受力最佳。 且不同锥角下的圆盘应力变化规律一致, 表明锥角对拉撑位置无明显影响。
结合拉撑截面SII、SIV和不同拉撑位置下单圈拉撑圆盘位移变形图,可以发现外端的拉撑作用要弱于盘片与轴管端的拉撑作用。
1.4 宽节比Lw/Lc对单圈拉撑圆盘拉撑件位置的影响
虽然不同拉撑位置下直径为1 000mm的圆盘结构最佳拉撑位置在L1/Lw=0.50,但详细应力分析表明盘片内侧的拉撑作用要强于外端的拉撑作用,当圆盘直径增大时,这种拉撑作用的差距可能更加明显的表现出来,为了确定单圈拉撑圆盘拉撑件的最佳位置,考虑不同宽节比Lw/Lc对于圆盘单圈拉撑位置设置的影响,圆盘分析模型参数详见表1。
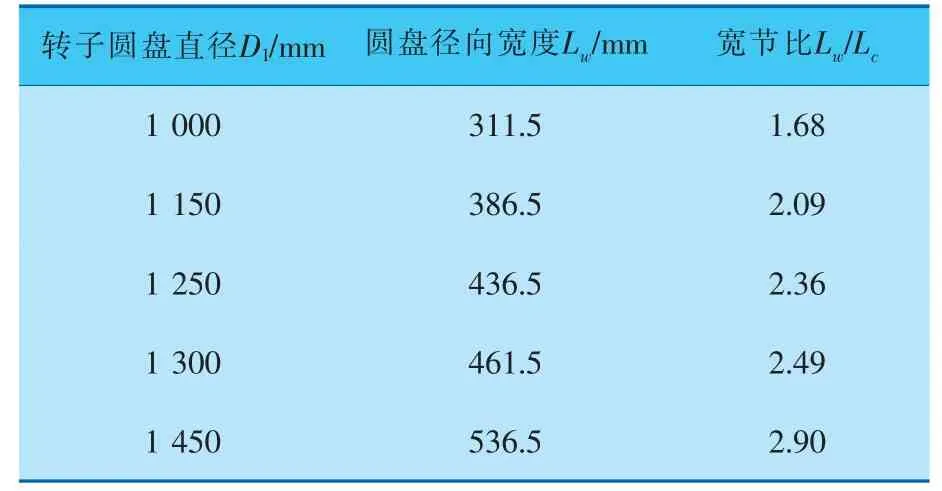
表1 不同宽节比Lw/Lc转子圆盘分析模型结构参数
由上节圆盘应力分析可知, 圆盘锥角α对于各部位应力随拉撑位置L1改变的变化趋势基本没有影响,随着盘片直径的增大,锥角变化范围有限,选择圆盘锥角α=12°的分析模型,在保证拉撑件周向间距Lc=185mm不变前提下,取圆盘直径D1分别为1 000、1 150、1 250、1 300、1 450mm的5种模型进行详细分析。
图4为不同宽节比Lw/Lc下盘片拉撑截面应力变化趋势。 随着Lw/Lc增大,使得圆盘的无拉撑区域增大,拉撑截面的应力相应增大。 当拉撑位置为L1/Lw=0.35时,应力均保持在各拉撑位置的最高水平,属于最劣拉撑位置;随着宽节比Lw/Lc增大,L1/Lw=0.40大于L1/Lw=0.65时的应力水平, 其增大趋势要大于相应的外侧拉撑部位,证实了外侧的拉撑强度要弱于内侧。
考虑最佳拉撑位置,以应力相对较小的L1/Lw分别为0.50、0.55、0.60为具体讨论对象,当宽节比Lw/Lc<2.40时,L1/Lw=0.50时的应力要小于其他两者, 此时最佳拉撑位置在L1/Lw=0.50处; 当Lw/Lc>2.40后, 随着宽节比增大,L1/Lw=0.50时应力增大幅度变大, 且L1/Lw=0.50的应力曲线开始与L1/Lw=0.55交汇,由此可以看出,对于Lw/Lc>2.40的单圈拉撑转子圆盘结构,圆盘内外侧拉撑强度的差异将更加明显, 其最佳拉撑位置将逐步向外侧转移,由最初的沿径向均布变为L1/Lw=0.55处。
1.5 单圈拉撑转子圆盘径向拉撑适宜位置
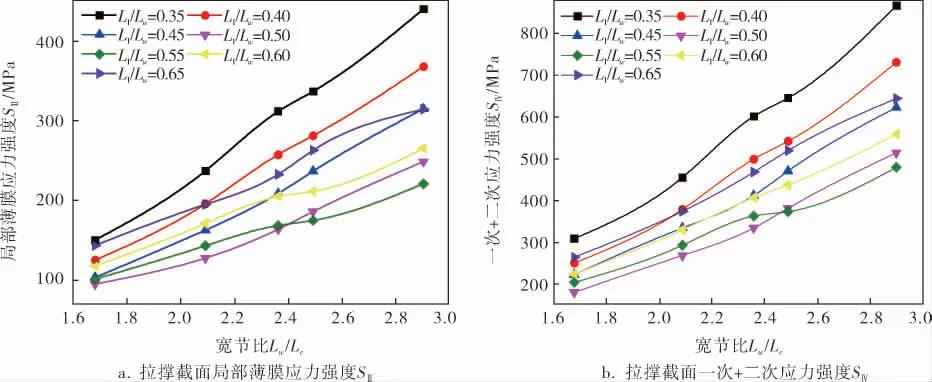
图4 α=12°时不同宽节比Lw/Lc下转子圆盘应力
通过有限元计算分析,发现圆盘锥角对拉撑位置的设置没什么影响;而宽节比对最佳拉撑位置影响显著,当宽节比Lw/Lc<2.40时,拉撑件径向适宜位置为L1/Lw=0.50;当Lw/Lc>2.40时,由于盘片内外侧拉撑强度的差异,外侧的拉撑强度弱于内侧,此时径向拉撑适宜位置为L1/Lw=0.55。
2 两圈拉撑圆盘的拉撑件径向适宜位置分析
考虑到单圈拉撑圆盘分析结果,内侧拉撑强度大于外侧,拉撑件沿圆盘径向均布时,外圈拉撑件和拉撑截面应力将大于内侧相应的应力,为此参照单圈拉撑分析方法,取内圈位置4水平、外圈位置5水平:L1/Lw=0.28、L1/Lw=0.33、L1/Lw=0.38、L1/Lw=0.43,L2/Lw=0.57、L2/Lw=0.62、L2/Lw=0.67、L2/Lw=0.72、L2/Lw=0.77,参照上节中宽节比对拉撑位置影响,等比例放大到两圈拉撑,取相应的4个宽节比Lw/Lc=2.92、Lw/Lc=3.22、Lw/Lc=3.73、Lw/Lc=4.14结构进行详细分析。
2.1 两圈拉撑转子圆盘位移变形分析
通过有限元计算结果可知,不同宽节比下最大位移随内圈、外圈拉撑位置变化的规律大抵相同,图5为宽节比Lw/Lc=2.92时4种典型拉撑位置下拉撑截面的变形。 图中L1/Lw=0.33、L2/Lw=0.67与L1/Lw=0.38、L2/Lw=0.72时的最大变形相近,只是前者最大位移出现在两圈拉撑件之间,后者出现在内圈拉撑件与轴管之间。
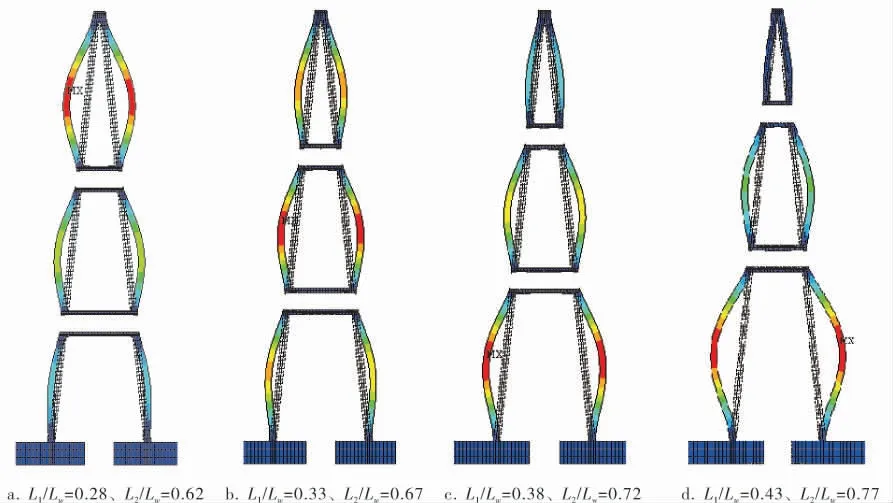
图5 Lw/Lc=2.92时典型拉撑截面变形
图6为宽节比Lw/Lc=2.92时最大位移随内、外圈位置变化的趋势,当内圈位置L1/Lw=0.28、外圈位置L2/Lw=0.62时位移最小, 其他最小位移的内、外圈拉撑位置分别为L1/Lw=0.33、L2/Lw=0.67;L1/Lw=0.38、L2/Lw=0.72;L1/Lw=0.43、L2/Lw=0.77,结合计算结果,若以最小位移变形为目标设置两圈拉撑件时,L1/Lw=0.33、L2/Lw=0.67与L1/Lw=0.38、L2/Lw=0.72处于同一水平,应该具体视应力水平变化趋势再做决定。
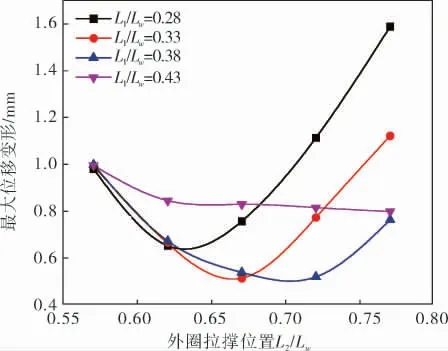
图6 Lw/Lc=2.92时不同拉撑位置下转子圆盘最大位移
2.2 两圈拉撑转子圆盘应力分析
图7~9给出了不同宽节比下拉撑截面应力随拉撑位置的变化规律。 由图中可以看出,各应力曲线的变化规律没有太大的差异。 内圈拉撑位置L1/Lw=0.28、L1/Lw=0.33、L1/Lw=0.38下应力随着外圈拉撑位置的增大均呈先下降后上升的趋势, 对应的“谷点”位置大概在L2/Lw=0.63、L2/Lw=0.67、L2/Lw=0.70附近;单圈拉撑圆盘适宜位置研究表明,内圈侧的拉撑差异会随着宽节比增大而逐步显现,对于两圈而言,此种拉撑差异也同样存在:当宽节比Lw/Lc>3.73后,L1/Lw=0.38时的应力曲线将逐渐拉开与L1/Lw=0.33时的距离, 此时最佳受力布置已不再是L1/Lw=0.33、L2/Lw=0.67, 而是两圈拉撑件整体向外侧偏移至L1/Lw=0.38、L2/Lw=0.70位置处。
2.3 两圈拉撑转子圆盘径向适宜位置
在两圈拉撑转子圆盘结构中,尽管径向均布拉撑件时最大位移最小,但这种情况并不是绝对意义上的最优,只是略微小于其他布置位置时的最大位移,数值上与L1/Lw=0.38时最小位移较为相近;内外侧拉撑和拉撑件拉撑作用的差异在小直径圆盘中展现的并不明显,故此时不必细究拉撑强度的差异,但随着宽节比增大,最佳拉撑位置将向外侧靠拢, 设计时应考虑拉撑强弱的差异。对于小宽节比的圆盘拉撑件均布即可,对于大宽节比的圆盘适宜拉撑位置设置在L1/Lw=0.38、L2/Lw=0.70处。
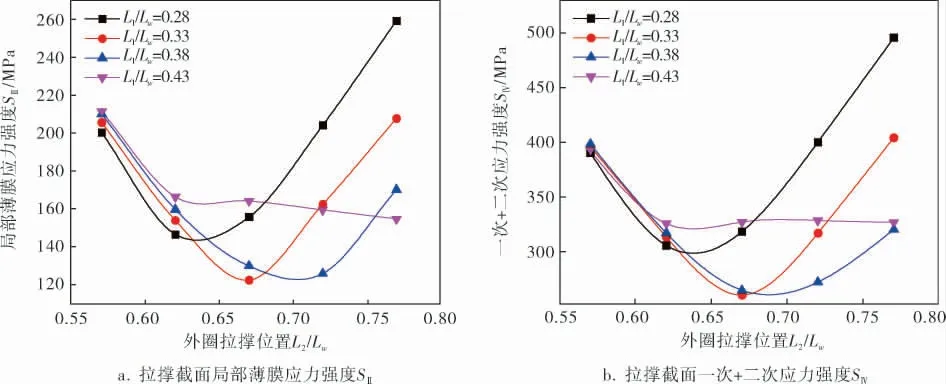
图7 Lw/Lc=2.92时不同拉撑位置下转子圆盘应力

图8 Lw/Lc=3.73时不同拉撑位置下转子圆盘应力

图9 Lw/Lc=4.14时不同拉撑位置下转子圆盘应力
3 结论
3.1 由于转子圆盘腔体高度沿径向逐渐减小,且内外侧拉撑强度有差异, 使得外端拉撑强度小于轴管侧对盘片的拉撑强度; 在圆盘所能达到的锥角变化范围内,锥角对最佳拉撑位置基本无影响。
3.2 在单圈拉撑转子圆盘结构中,对于宽节比Lw/Lc<2.40的小尺寸圆盘, 可以不用考虑拉撑差异导致最佳拉撑位置的偏移, 此时径向拉撑最佳位置为L1/Lw=0.50;对于宽节比Lw/Lc>2.40的大尺寸圆盘,由于盘片内外侧拉撑的差异,外侧的拉撑强度弱于内侧,所以径向拉撑最佳位置为L1/Lw=0.55。
3.3 两圈拉撑转子圆盘结构中, 当宽节比Lw/Lc<3.73时,内外侧拉撑作用的差异并不明显,此时径向拉撑最佳位置在L1/Lw=0.33,L2/Lw=0.67处;随着宽节比增大,当Lw/Lc>3.73,最佳拉撑位置将向外侧靠拢,设计时因考虑到拉撑强弱的差异,此时径向拉撑最佳位置在L1/Lw=0.38、L2/Lw=0.70处。

