基于SPH方法对多晶硅裂纹扩展的数值模拟

，， ， ，

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

多晶硅作为光伏设备的基材，需要在无污染的环境中破碎成一定尺寸才能使用，一般要求碎块尺寸为5～90 mm。由于对多晶硅的加工过程要求较高，目前企业基本采用人工敲击的方式对其进行破碎处理，而因敲击造成的材料尺寸不符合要求形成的浪费比例约为10%。为了能减少多晶硅材料的浪费，并提高工作效率，操作人员必须掌握多晶硅的破碎机理。多晶硅等高脆性材料在冲击载荷下的损伤破碎过程，一般是损伤、损伤累积、破碎、失效、主裂纹以及主裂纹群扩展发生的过程，类似于岩石等脆性材料的产生、扩展、断裂的过程[1]。

国内外许多学者对脆性材料的裂纹扩展做了深入研究。如李运禄等[2]对混凝土在不同速度冲击载荷下的裂纹形成过程进行了数值模拟。王石安等[3]研究了不同冲击速度对花岗岩靶板裂纹扩展以及起裂位置的影响。袁琳等[4]研究了不同材料的力学性质、材料均质度、入射应力脉冲幅值和历时对II型裂纹动态扩展的影响。C.Daux等[5]建立了用于分叉和交叉裂纹问题的扩展有限元法。F.Kun等[6]、B.Behera等[7]和N.Sator等[8]分别采用离散元法和分子动力学方法模拟分析了二维圆盘的冲击破碎，发现其存在一个临界冲击速度（动能），可以将材料的冲击响应分为局部损伤和整体碎裂两种状态。陈兴等[9]研究了脆性材料在冲击破碎的作用下，材料无序性对临界冲击速度、破碎模式、碎片形态、裂纹的形成与扩展的影响。秦飞等[10]用边界元法模拟分析了多裂纹的扩展情况。但关于多晶硅内部裂纹扩展机理方面的研究文献较少。

多晶硅肉眼观察呈灰色，有金属光泽，莫氏硬度为7，类比岩石类材料，其硬度在锗和石英之间。常温下多晶硅硬而脆，做切割时易发生碎裂[11]。多晶硅等脆硬性材料的破碎是一种应变率较高、形变量较大的过程。因有限差分法（finite difference method，FDM）和有限元法（finite element method，FEM）对于处理高应变率、大形变等问题时，会出现网格扭曲、计算精度下降、计算难以继续，所以不适合被用于脆硬性材料的数值模拟。而光滑粒子流体动力学（smoothed partcle hydrodynamic method，SPH）作为一种拉格朗日形式的无网格粒子法，可以模拟连续体结构的解体、破碎、固体的层裂、脆性断裂等大形变问题，同时可以规避画网格导致的网格缠绕和扭曲等问题，可被用于处理脆硬性材料。W.Benz[12]等首次使用SPH方法对脆性材料进行了数值模拟，提出了处理脆性断裂的方法。其后，SPH方法被广泛地应用于结构脆性断裂计算与分析中。

本研究中，冲击破碎的多晶硅为均值脆性材料，其抗拉强度和抗剪强度远小于抗压强度。故本研究采用SPH算法、Johnson-Homquist II（JH-2模型）损伤本构模型，利用非线性动力学软件Autodyn-2D，对多晶硅材料用平面锤头在不同速度冲击作用下进行裂纹扩展的数值模拟，探讨多晶硅裂纹产生的临界速度，分析裂纹产生、扩展的过程及冲击速度等对裂纹产生的影响，以期为降低多晶硅破碎损失率和提高破碎效率提供理论参考依据。

2 SPH 基本方程

SPH方法以核函数为基础，将整个流场的固体、流体离散为一系列具有物理特性（质量、速度和能量）的粒子，每个互不连接的粒子代表一个插值点。其中，用于估计粒子运动信息的核近似算子表达式为

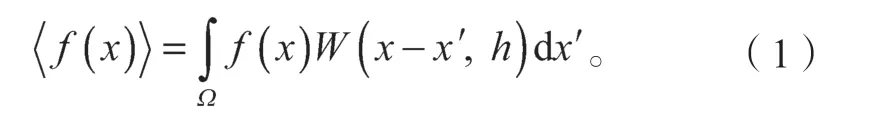
式中：Ω为积分域（支持域）；

h为光滑长度；

W为光滑核函数。

W可用辅助函数θ(x)定义如下：

式（2）（3）中：C为归一化常数；

W(x，h)为单峰函数，W常选用偶函数，并满足条件式（4）～（6）。

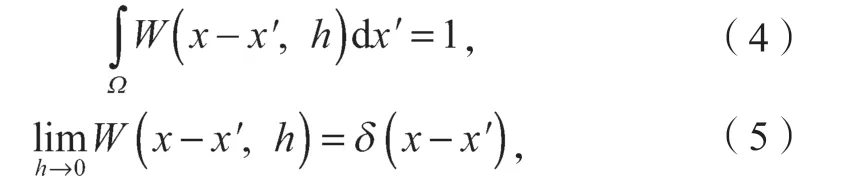
式（5）（6）中：k是与点x处光滑函数相关的常数，表示光滑函数的有效范围；

δ为狄拉克函数。

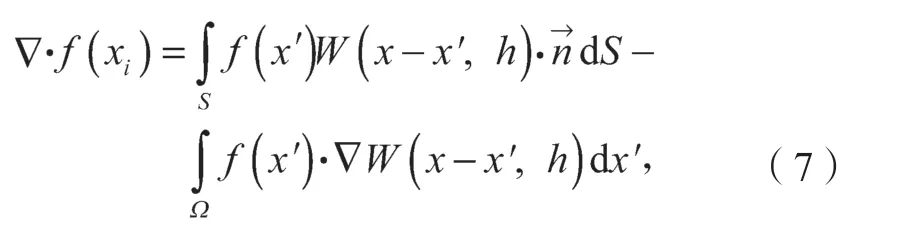
由于光滑函数W定义在支持域内，故当支持域位于问题域内部时（如图1所示），公式（7）右边的面积积分为0。故有

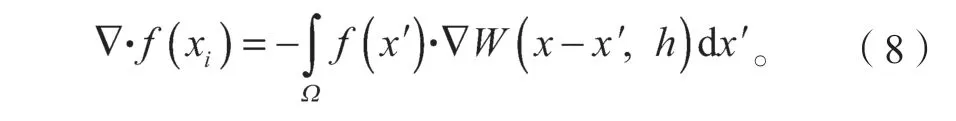
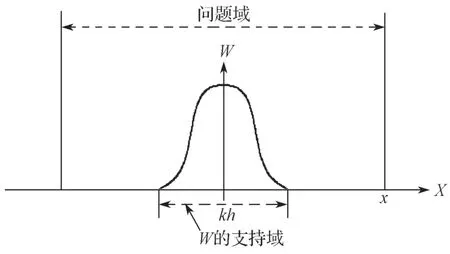
图1 光滑函数W的支持域和问题域Fig.1 Support and problem domains for smooth function W

为了利用粒子近似法使得整个系统由具有独立的质量、占有独立空间的有限个粒子进行表示。本文利用粒子的叠加求和离散化过程，引入粒子的质量和密度以赋予粒子质量，并避免出现数值积分的背景网格，将核近似法转化为粒子近似法，其粒子i处的函数粒子近似式为

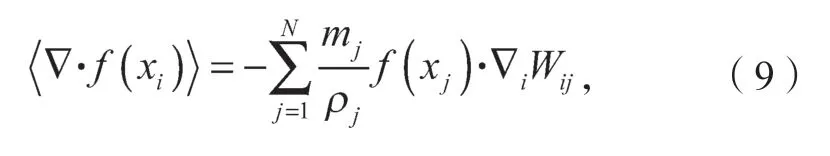
其中

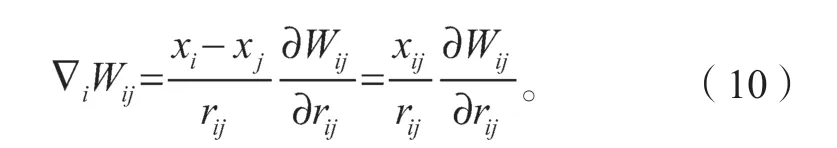
式（9）（10）中：mj为粒子j的质量；

ρj为粒子j的密度；

N为支持域中的粒子总量；

Wij为i粒子离散为支持域内j粒子的光滑函数；

rij为两粒子间的距离。

其中式（9）表明，粒子i处的函数梯度值可通过应用光滑函数的梯度对粒子i的支持域内所有粒子函数的加权平均近似得出。

控制体（材料粒子）可伴随流体的流动一起运动，但一直保持物质的总质量不变，而控制面的改变又会引起控制体的体积变化。考虑到材料的弹塑性效应，用具有拉格朗日性质的流体动力学连续介质方程组（Navier-Stokes 方程）对物质点进行描述，可提高自由边界和相同材料粒子密度不连续交界面的精度、降低粒子不一致的误差等，其公式表示如下：

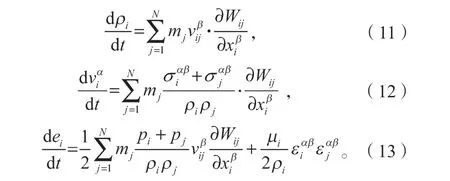
式（11）～（13）中：vij为粒子间的相对速度；

σ为总应力张量；

α和β为坐标方向；

p为各向同性压力；

μ为黏度系数；

ε为剪应变率；

e为比内能。

3 材料模型及参数选取

3.1 平面锤的本构模型及参数

由于钨合金（硬质合金）的密度、硬度远高于多晶硅的，敲击多晶硅不会破坏钨合金锤，即不会掉下金属粉末污染多晶硅，因此选择钨合金作为平面锤的材料。为有效仿真钨合金材料在冲击作用下产生的形变和损伤，引入Johnson-Cook材料本构模型，其应力-应变的函数关系表示如下：

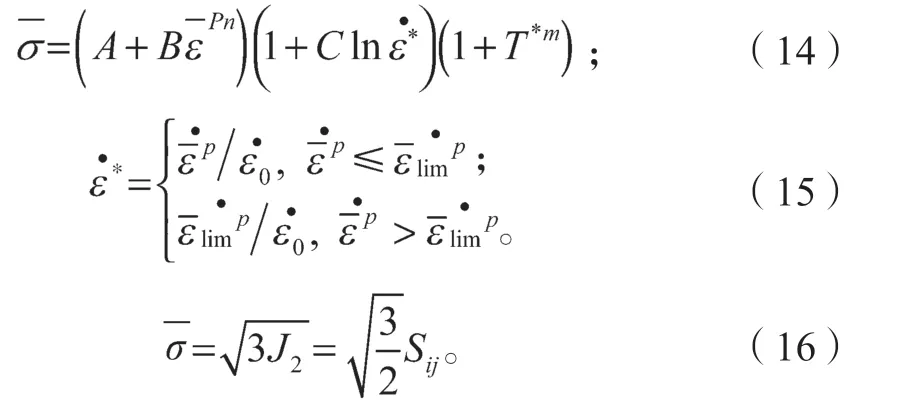
式（14）～（16）中：A、B、C、n、m为材料参数；

J2为偏应力张量的第二不变量；

Sij为偏应力张量；

T*为无量纲温度，且，其中TR为室内温度，TM为熔化温度。

课题组对钨合金锤采用Shock 状态方程和Johnson-Cook 本构模型予以描述，Autodyn 材料库中其参数分别如表1和表2所示。

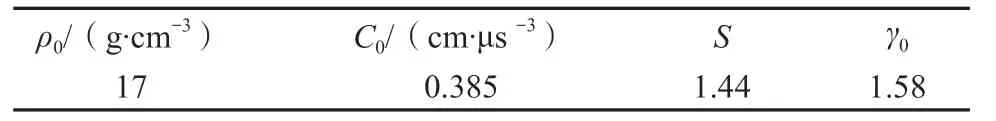
表1 Shock状态方程参数Table1 Shock state equation parameters

表2 Johnson-Cook本构模型参数Table2 Johnson-Cook constitutive model parameters

3.2 多晶硅的本构模型及参数

为更好地描述材料所受的等效应力与损伤累积间的关系，本研究引入与等效应力与应变率及损伤因子D相关的Johnson-Homquist II（JH-2）本构模型表示多晶硅等脆性材料的动态损伤过程。其定义的无量纲材料强度σ*[12]模型如下：

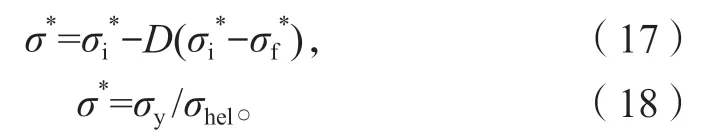
式（17）（18）中：σi*为初始强度；

σf*为断裂强度；

D为损伤变量，且0 ≤D≤1；

σy为真实强度；

σhel为雨贡弹性极限强度。

当D=0（未损伤）时，多晶硅的初始强度（等效应力）为

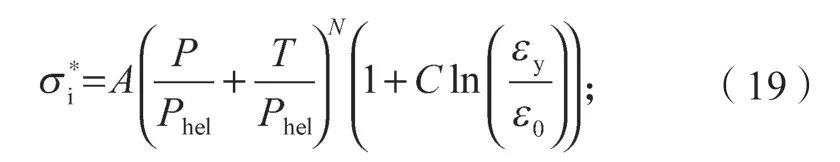
而当D=1（完全断裂）时，多晶硅的断裂强度（等效应力）为

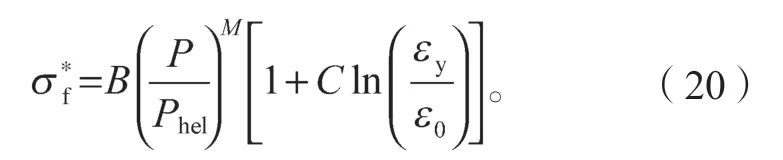
式（19）（20）中：A、B、C、M、N为材料参数；

εy为真实应变率；

ε0为参考应变率，此处取1.0 s-1；

T为最大拉伸强度；

Phel为材料处于Hugoniot 弹性极限时的压力；

P/Phel为静粹压力，其中P为实际压力。

本研究中，多晶硅材料受到冲击作用从开始压缩到破碎的整个过程，可分为3个阶段：线弹性阶段、塑性过渡阶段、完全压实材料阶段。

线弹性阶段多晶硅未损伤（D=0）时，多晶硅所受压力的状态方程表示为

式中：K为材料体积模量；

ρ为多晶硅当前密度；

ρ0为多晶硅初始密度；

ρ/ρ0-1为体应变。

塑性过渡阶段，材料会产生不可逆的形变（D＞0），开始损伤积累并出现微裂纹，此时材料的压力状态方程和损伤变量D与塑性应变的关系如下：

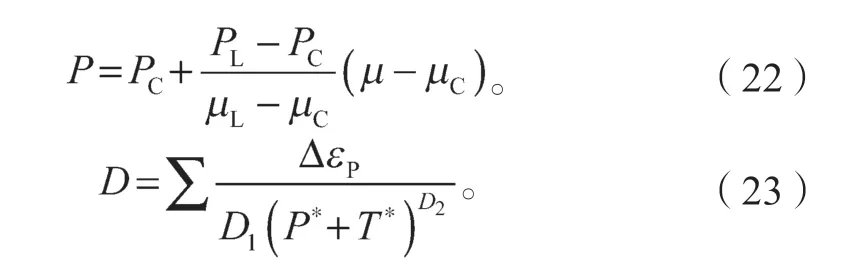
式（22）～（23）中：PC为压碎点压力；

PL为压实点压力；

μ为体积应变；

μC为压碎点的体积应变；

μL为压实点的体积应变；

D1、D2为损伤常量；

ΔεP为塑性应变增量；

D1(P*+T*)D2为断裂时的塑性应变。

完全压实材料阶段，材料内部损伤积累的微裂纹逐渐延伸扩展且相互交叉贯通形成明裂缝，多晶硅逐渐破碎开来（D=1）。此时材料所受压力关系式为

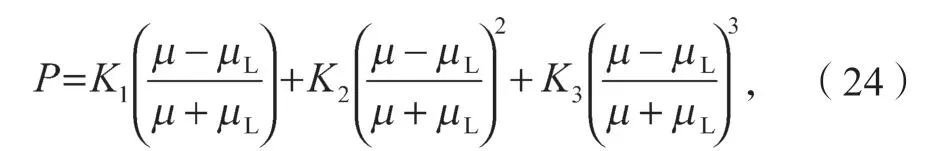
式中K1、K2、K3均为材料常数。

本研究中对多晶硅材料用Linear 状态方程和Johnson-Homquist Ⅱ损伤本构模型予以描述，其相关参数见表3和表4。

表3 Linear状态方程参数Table3 Linear state equation parameters

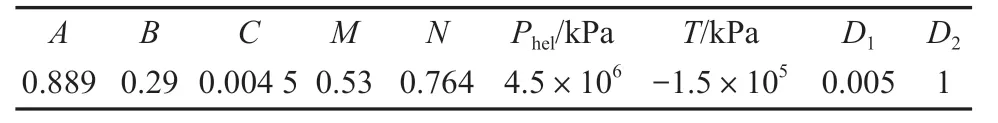
表4 多晶硅Johnson-Homquist Ⅱ本构模型参数Table4 Johnson-Homquist-2 constitutive model parameters of Polycrystalline silicon

4 数值仿真及结果分析

4.1 计算模型

为使多晶硅破碎后碎片尺寸尽量为4～100 mm，本研究利用非线性动力学软件Autodyn-2D 建立了钨合金锤冲击多晶硅靶板的几何模型，并且进行了离散化处理。其中钨合金平头锤宽15 mm，高10 mm；多晶硅靶板宽100 mm，高120 mm。模型平面对称，粒子尺寸为0.3 mm，其离散化后的粒子总数为134 850个。

4.2 模拟结果与分析

4.2.1 冲击破碎过程

图2为平头锤以40 m/s的速度竖直冲击多晶硅靶板，多晶硅的破碎及裂纹演化过程。

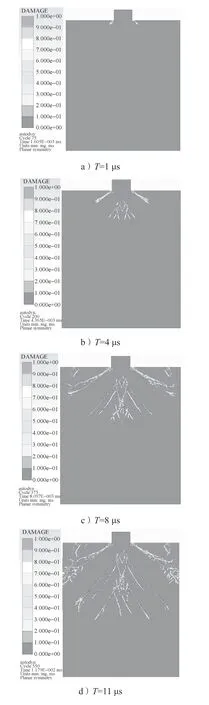
图2 冲击损伤裂纹扩展过程图Fig.2 Process diagram of crack propagation with an impact damage

由图2可以得知，当用平头锤以40 m/s的速度冲击多晶硅靶板时，首先在与多晶硅靶板接触区域的两端产生严重的局部损伤（如图2a，T=1 μs时所示）；随后，裂纹沿着两端损伤向靶板的两侧进行扩展，直至靶板的两侧边界形成“八”字形裂纹，同时接触区域下部萌生出微裂纹并形成“∧”形主裂纹。随着损伤的积累，主裂纹迅速向下延伸扩展，然后主裂纹再缓慢扩展，直至贯穿整个靶板。同时，碎块间的相对碰撞会让几条“∧”形裂纹产生分叉裂纹并且连通相邻的“∧”形裂纹。整个冲击过程中，在1～18 μs时间段，裂纹扩展速度不断增加；在18～26 μs时间段，裂纹扩展速度慢慢减小；到26～31 μs时段时，裂纹几乎停止扩展，此时已经达到40 m/s 冲击速度的破碎极限。

4.2.2 冲击速度对多晶硅裂纹的影响

为研究锤头锤击速度对多晶硅裂纹扩展的影响，用宽度为15 mm的锤头，竖直向着靶板中心以着靶速度分别为5,10,15,20,25,30,35,40,45,50 m/s的10种情况进行数值模拟，得到T=60 μs时的仿真结果如图3所示。

图3 不同速度冲击时的损伤裂纹扩展图Fig.3 Fracture expansion map of impact damage at different velocities

由图3可以得知，冲击速度对多晶硅裂纹的扩展影响很大。冲击速度越大，主裂纹延伸的长度越长，微裂纹、分叉裂纹扩展越密集，多晶硅破碎后的粒度越细，破碎的时间越短，破碎也越彻底。当冲击速度小于5 m/s时，多晶硅处于线弹性阶段（未出现损伤）；当冲击速度增大但小于10 m/s时，多晶硅处于塑性过渡阶段，受冲击作用产生不可逆形变，开始出现损伤积累并缓慢出现微裂纹。当冲击速度增至10 m/s时，多晶硅内部的微裂纹交错延伸并交汇贯通形成明显的裂纹，开始起裂。当冲击速度为10～25 m/s时，主裂纹开始向靶板底部扩展的长度和破碎程度快速增加，形成相对较多的明显“∧”形裂纹。当冲击速度大于25 m/s 后，主裂纹扩展的递增速率明显减慢。当冲击速度继续增大到30 m/s时，起裂点的位置开始从多晶硅靶板顶部两端向轴线中心移动，直至起裂点到达接触区域的两端。而当冲击速度增至40 m/s时，主裂纹基本停止扩展，此时碎片尺寸为5～90 mm的破碎程度最大；当冲击速度大于40 m/s时，主裂纹的周围和末端出现许多微小裂纹，此时产生许多粉碎性碎片（尺寸小于5 mm）。

研究碎片大小随冲击速度的变化情况时，由于多晶硅靶板为均质材料，故用碎片的质量占靶板质量的比例（mt/m）表示碎片的大小以及破碎效果。碎片质量集合的P阶矩阵和碎片的平均质量定义如下：

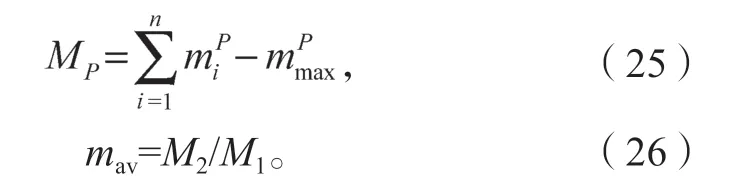
式（25）（26）中：n为碎片数量；

mi为第i个碎片质量；

mmax为最大碎片质量；

mav为平均碎片质量。

图4所示为最大碎片、第二大碎片及平均碎片质量随冲击速度的变化曲线。

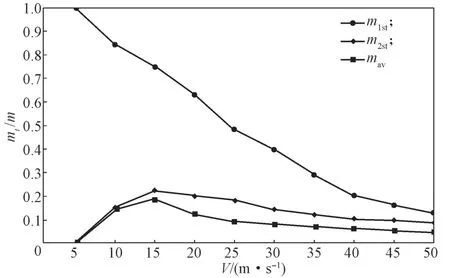
图4 最大碎片、第二大碎片及平均碎片质量随冲击速度的变化曲线Fig.4 Change curves of the mass of the largest,second largest and average fragments with the velocities

由图4可知，随着冲击速度增加，最大碎片质量（m1st）持续减小，第二大碎片质量（m2st）和平均碎片质量（mav）先增大后减小，并在速度为40 m/s时趋于稳定不变状态，而此时最大碎片质量达到较小的值并开始缓慢减小，此时破碎效果最佳。

4.2.3 冲击点对多晶硅裂纹的影响

为研究冲击点对多晶硅裂纹扩展的影响，将锤头中心线与多晶硅左侧边界的水平距离记作D，选取D为7.5,25,50 mm 3种情况，以40 m/s的冲击速度进行数值仿真，其中30 μs时的仿真结果见图5。

图5 不同冲击点损伤裂纹扩展图Fig.5 Traumatic crack propagation at different impact points

由图5可知，随着锤头位置往靶板中间移动，多晶硅破碎效果越来越好。当D=7.5 mm时，几条主裂纹几乎平行地从左上方向右下方进行扩展，右上方大块靶板几乎没有破碎，而左侧边缘处呈粉碎性破碎；当D=25 mm时，开始在靶板上部出现“∧”形主裂纹，出现了少量的裂纹交叉贯通，左侧边缘处碎片尺寸过小；当D=50 mm时，几条“∧”形裂纹产生分叉裂纹，并连通相邻的“∧”形裂纹，碎块数量大大增加，碎片尺寸大小相对适中，此时的破碎效果最好。

4.2.4 锤头宽度对多晶硅裂纹的影响

本研究中分别用锤头宽度S为5,15,20,25,30,40,50,60 mm的锤头，以40 m/s的速度冲击多晶硅靶板进行数值模拟，得到T=60 μs时的裂纹扩展模拟结果如图6所示。

图6 不同锤头宽度冲击损伤裂纹扩展图Fig.6 Fracture propagation of impact damage with different hammer head widths

由图6可以得知，随着锤头宽度的增加，裂纹密度增大，碎片粒度尺寸减小。当锤头宽度为5 mm时，因冲击产生的裂纹比较稀疏，以“∧”形裂纹为主；当S=20 mm时，裂纹扩展停止，碎片尺寸相对适中；当S＞25 mm时，主要的裂纹附近开始形成许多微小裂纹，碎片的粒度尺寸随着锤头宽度的不断增加而减小；随着锤头宽度增加，裂纹密度也不断增加；当S＞60 mm时，裂纹分布过于密集，导致破碎后的碎片过小甚至成粉末状。因此，锤头存在一个最佳宽度，使得裂纹分布更加均匀且碎片尺寸适中，即锤头宽度约为20 mm。

5 结论

1）本研究采用可以规避冲击过程中网格畸变的SPH方法结合Johnson-Homquist II模型，能有效地反映裂纹的形成以及扩展过程。

2）冲击速度影响着裂纹的起裂速度，起裂点离中心轴线越近，则“∧”形裂纹的扩展长度越长，且碎片的密度越大。

3）锤头的宽度越大，破碎后形成的碎片粒度越小，裂纹的密度越大。

4）锤头的锤击位置越靠近中心轴线，破碎后碎片的尺寸更为合理，破碎效果更好。

5）主“∧”形裂纹的扩展速度随着冲击速度的增加而增加，当冲击速度达到一定值时，主“∧”形裂纹扩展速度先增加然后基本保持不变。

6）当用宽为20 mm 左右的锤头以40 m/s的速度冲击多晶硅靶板的最中间位置时，破碎后尺寸为5～90 mm的多晶硅碎片所占比例最大。